江苏省镇江市丹阳市华南实验教育集团2024—2025学年九年级上学期期中考试数学试题

这是一份江苏省镇江市丹阳市华南实验教育集团2024—2025学年九年级上学期期中考试数学试题，共28页。试卷主要包含了cm等内容，欢迎下载使用。
1．（3分）一元二次方程x2+2x﹣1＝0的根的情况是（ ）
A．只有一个实数根
B．有两个相等的实数根
C．有两个不相等的实数根
D．没有实数根
2．（3分）如图，点A，B，C都在⊙O上，∠AOB＝130°，则∠ACB的大小是（ ）
A．50°B．55°C．60°D．65°
3．（3分）用配方法解方程x2+8x+7＝0，则配方正确的是（ ）
A．（x+4）2＝9B．（x﹣4）2＝9C．（x﹣8）2＝16D．（x+8）2＝57
4．（3分）如图，D是△ABC边AB上一点，添加一个条件后，仍不能使△ACD∽△ABC的是（ ）
A．∠ACD＝∠BB．∠ADC＝∠ACBC．D．AC2＝AD•AB
5．（3分）黄金分割被很多人认为是“最美比例”，是因为它符合人们的视觉习惯和审美心理，能够创造出更加和谐、平衡和美观的艺术作品和产品．在自然界中黄金分割也很常见，如图是一个有着“最美比例”的鹦鹉螺，点B是线段AC的黄金分割点，AB＞BC，若AC＝16cm，那么AB的长为（ ）cm．
A．B．C．D．
6．（3分）如图，点B、C、D在⊙O上，∠ADB＝30°，A是的中点，若OB＝1，则的长是（ ）
A．B．C．D．2π
7．（3分）如图，在直角坐标系中，△OCD的顶点为O（0，0），C（﹣4，﹣3），D（﹣3，0），以点O为位似中心，在第一象限内作△OCD的位似图形△OAB，位似比为1：3，则点A坐标为（ ）
A．（9，9）B．（12，9）C．（9，12）D．（12，12）
8．（3分）如图是一把折叠椅子及其侧面的示意图，把一个简易刻度尺与地面AB垂直放置，其中AB与“0”刻度线重合，O点落在“3”刻度线上，CD与“5”刻度线重合，若测得AB＝50cm，则CD的长是（ ）
A．30cmB．C．20cmD．
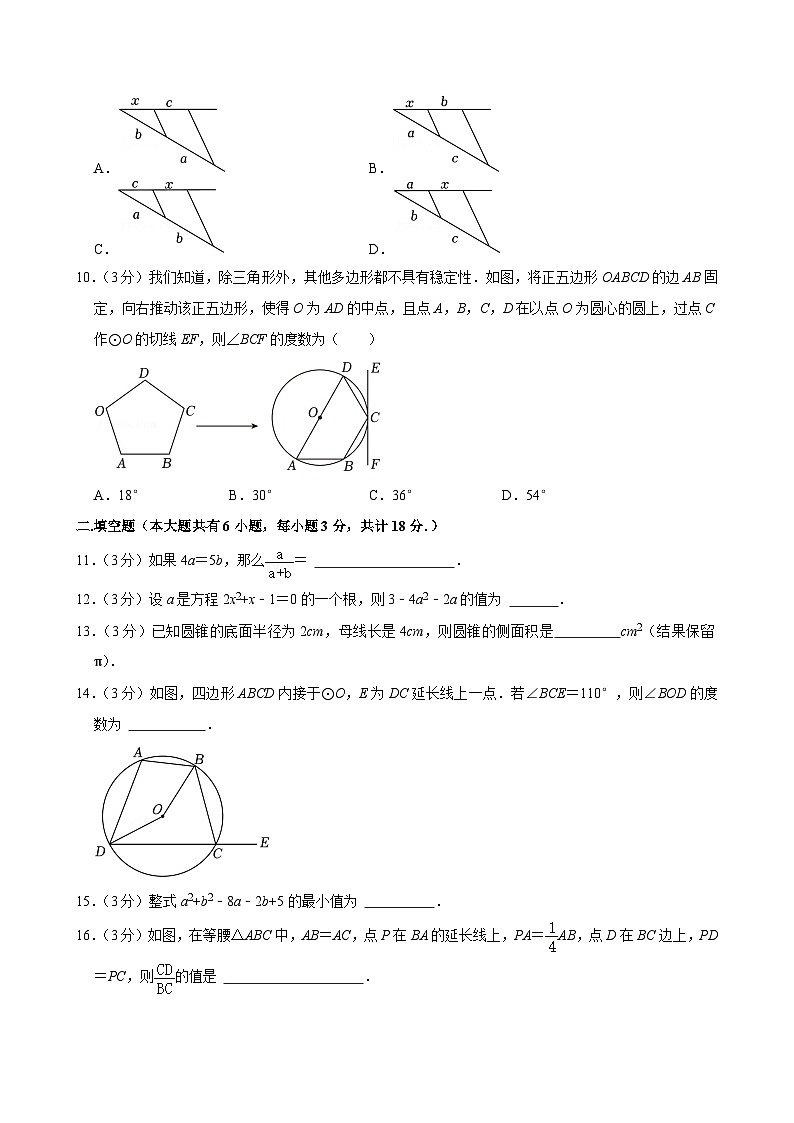
9．（3分）已知线段a，b，c，求作线段x，使，下列作图中正确的是（ ）
A．B．
C．D．
10．（3分）我们知道，除三角形外，其他多边形都不具有稳定性．如图，将正五边形OABCD的边AB固定，向右推动该正五边形，使得O为AD的中点，且点A，B，C，D在以点O为圆心的圆上，过点C作⊙O的切线EF，则∠BCF的度数为（ ）
A．18°B．30°C．36°D．54°
二.填空题（本大题共有6小题，每小题3分，共计18分．）
11．（3分）如果4a＝5b，那么＝ ．
12．（3分）设a是方程2x2+x﹣1＝0的一个根，则3﹣4a2﹣2a的值为 ．
13．（3分）已知圆锥的底面半径为2cm，母线长是4cm，则圆锥的侧面积是 cm2（结果保留π）．
14．（3分）如图，四边形ABCD内接于⊙O，E为DC延长线上一点．若∠BCE＝110°，则∠BOD的度数为 ．
15．（3分）整式a2+b2﹣8a﹣2b+5的最小值为 ．
16．（3分）如图，在等腰△ABC中，AB＝AC，点P在BA的延长线上，PA＝AB，点D在BC边上，PD＝PC，则的值是 ．
三、解答题（本大题共有10小题，共计72分．解答时应写出必要的文字说明、证明过程或演算步骤．）
17．（8分）解方程：
（1）5x2﹣3x＝x+1．
（2）3x（x﹣2）＝2（2﹣x）．
18．（6分）已知关于x的一元二次方程x2+mx+2m﹣7＝0．
（1）求证：该方程总有两个不相等的实数根
（2）已知方程的一个根为x＝2，求m值及方程的另一根．
19．（6分）如图，在△ABC中，D，E分别是边AB，AC上的点，连接DE，且∠ADE＝∠ACB．
（1）求证：△ADE∽△ACB；
（2）若AD＝2DB，AE＝4，AC＝9，求BD的长．
20．（6分）如图，在坐标系中，A（1，6）、B（5，6）、C（7，4）．
（1）经过A、B、C三点的圆弧所在圆的圆心M的坐标为 ；
（2）这个圆的半径为 ；
（3）直接判断点D（5，﹣3）与⊙M的位置关系．点D（5，﹣3）在⊙M ．（填内、外、上）
21．（6分）智慧养老，让老年人享受数字经济红利．近年来，智慧养老成为老龄事业与产业发展的方向之一，广东省正致力于打造智慧养老的新标杆，为老年人提供更加贴心、高效的养老服务，同时为数字经济的发展注入新活力．某养老服务机构8月份为800名老人提供服务，10月份为1352名老人提供服务，求该机构9、10月份服务老人人数的月平均增长率．
22．（6分）学完图形变换后，小宛以“正五边形的变换”为主题开展探究活动：
（1）如图1，将正五边形纸片ABCDE折叠，使点B与点E重合，折痕为AM，展开后，再将纸片折叠，使边AB落在线段AM上，点B的对应点为点B，折痕为AF，求∠AFB的大小．
（2）如图2，用一些全等的正五边形按图示方式拼接，使相邻的两个正五边形有公共顶点，所夹的锐角为24°，图中所示的是前3个正五边形拼接的情况，若拼接一圈后，中间能形成一个正多边形，请直接写出这个正多边形的边数．
23．（8分）在Rt△AFD中，∠F＝90°，点B、C分别在AD、FD上，以AB为直径的半圆O过点C，连接AC，将△AFC沿AC翻折得△AEC，且点E恰好落在直径AB上．
（1）判断：直线FC与半圆O的位置关系是 ；并证明你的结论．
（2）若OB＝BD＝2，求CE的长．
24．（8分）
25．（9分）如图，已知∠PAQ及AP边上一点C．
（1）尺规作图：（保留作图痕迹，不写作法）
①作⊙O，使得圆心O在射线AQ上，且⊙O经过A、C两点，交射线AQ于点B；
②在射线CP上求作点M，使点M到点C的距离与点M到射线AQ的距离相等；
（2）在（1）的条件下，若AC＝4，AB＝5，直接写出OM的长＝ ．
26．（9分）“关联”是解决数学问题的重要思维方式．角平分线的有关联想就有很多…
【问题提出】
（1）如图①，PC是△PAB的角平分线，求证：．
请根据小明或小红的思路，选择一种并完成证明．
【尝试应用】
（2）如图②，在Rt△ABC中，∠ACB＝90°，D是边AB上一点，连结CD，将△ACD沿CD所在直线折叠，使点A恰好落在边BC的中点E处．若DE＝5，求AC的长．
【拓展提高】
（3）如图③，△ABC中，AB＝6，AC＝4，AD为∠BAC的角平分线．AD的垂直平分线EF交BC延长线于点F，连接AF，当BD＝3时，AF的长为 ．
2024-2025学年江苏省镇江市丹阳市华南实验教育集团九年级（上）期中数学试卷
参考答案与试题解析
一．选择题（本大题共有10小题，每小题3分，共计30分，在每小题所给出的四个选项中恰有一项符合题目要求．）
1．（3分）一元二次方程x2+2x﹣1＝0的根的情况是（ ）
A．只有一个实数根
B．有两个相等的实数根
C．有两个不相等的实数根
D．没有实数根
【分析】根据方程的系数结合根的判别式，可得出Δ＝8＞0，进而可得出一元二次方程x2+2x﹣1＝0有两个不相等的实数根．
【解答】解：∵a＝1，b＝2，c＝﹣1，
∴Δ＝b2﹣4ac＝22﹣4×1×（﹣1）＝8＞0，
∴一元二次方程x2+2x﹣1＝0有两个不相等的实数根．
故选：C．
【点评】本题考查了根的判别式，牢记“当Δ＞0时，方程有两个不相等的实数根”是解题的关键．
2．（3分）如图，点A，B，C都在⊙O上，∠AOB＝130°，则∠ACB的大小是（ ）
A．50°B．55°C．60°D．65°
【分析】利用圆周角定理计算即可．
【解答】解：∵∠ACB＝∠AOB，∠AOB＝130°，
∴∠ACB＝65°．
故选：D．
【点评】本题考查圆周角定理，解题的关键是熟练掌握基本知识，属于中考常考题型．
3．（3分）用配方法解方程x2+8x+7＝0，则配方正确的是（ ）
A．（x+4）2＝9B．（x﹣4）2＝9C．（x﹣8）2＝16D．（x+8）2＝57
【分析】本题可以用配方法解一元二次方程，首先将常数项移到等号的右侧，将等号左右两边同时加上一次项系数一半的平方，即可将等号左边的代数式写成完全平方形式．
【解答】解：∵x2+8x+7＝0，
∴x2+8x＝﹣7，
⇒x2+8x+16＝﹣7+16，
∴（x+4）2＝9．
∴故选：A．
【点评】此题考查配方法的一般步骤：
①把常数项移到等号的右边；
②把二次项的系数化为1；
③等式两边同时加上一次项系数一半的平方．
选择用配方法解一元二次方程时，最好使方程的二次项的系数为1，一次项的系数是2的倍数．
4．（3分）如图，D是△ABC边AB上一点，添加一个条件后，仍不能使△ACD∽△ABC的是（ ）
A．∠ACD＝∠BB．∠ADC＝∠ACBC．D．AC2＝AD•AB
【分析】直接利用相似三角形的判定方法分别分析得出答案．
【解答】解：A、当∠ACD＝∠B时，再由∠A＝∠A，可得出△ACD∽△ABC，故此选项不合题意；
B、当∠ADC＝∠ACB时，再由∠A＝∠A，可得出△ACD∽△ABC，故此选项不合题意；
C、当时，无法得出△ACD∽△ABC，故此选项符合题意；
D、当AC2＝AD•AB时，即，再由∠A＝∠A，可得出△ACD∽△ABC，故此选项不合题意；
故选：C．
【点评】此题主要考查了相似三角形的判定，正确掌握相似三角形的判定方法是解题关键．
5．（3分）黄金分割被很多人认为是“最美比例”，是因为它符合人们的视觉习惯和审美心理，能够创造出更加和谐、平衡和美观的艺术作品和产品．在自然界中黄金分割也很常见，如图是一个有着“最美比例”的鹦鹉螺，点B是线段AC的黄金分割点，AB＞BC，若AC＝16cm，那么AB的长为（ ）cm．
A．B．C．D．
【分析】根据黄金分割的定义得到AB＝AC，把AC＝16代入计算即可得到答案．
【解答】解：∵点B是线段AC的黄金分割点（AB＞BC），
∴AB＝AC，
∵AC＝16，
∴AB＝×16＝8﹣8，
故选：C．
【点评】本题考查了黄金分割的有关计算，掌握黄金分割的定义是解决本题的关键．
6．（3分）如图，点B、C、D在⊙O上，∠ADB＝30°，A是的中点，若OB＝1，则的长是（ ）
A．B．C．D．2π
【分析】连接OA，由圆周角定理得∠AOB＝2∠ADB＝60°，由＝，求出∠BCD＝120°，再根据弧长公式计算即可．
【解答】解：如图，连接OA，
∵∠ADB＝30°，
∴∠AOB＝2∠ADB＝60°，
∵A是的中点，
∴＝，
∴∠AOC＝∠AOB＝60°，
∴∠BOC＝120°，
∴的长为＝π．
故选：A．
【点评】本题考查弧长的计算和圆周角定理，关键是由圆周角定理得到∠BOC＝120°和熟练掌握弧长公式．
7．（3分）如图，在直角坐标系中，△OCD的顶点为O（0，0），C（﹣4，﹣3），D（﹣3，0），以点O为位似中心，在第一象限内作△OCD的位似图形△OAB，位似比为1：3，则点A坐标为（ ）
A．（9，9）B．（12，9）C．（9，12）D．（12，12）
【分析】根据位似变换的性质计算即可．
【解答】解：以点O为位似中心，在第一象限内作△OCD的位似图形△OAB，位似比为1：3，点C的坐标为（﹣4，﹣3），
则点A坐标为（﹣4×（﹣3），（﹣3）×（﹣3）），即（12，9），
故选：B．
【点评】本题考查的是位似变换，在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k，那么位似图形对应点的坐标的比等于k或﹣k．
8．（3分）如图是一把折叠椅子及其侧面的示意图，把一个简易刻度尺与地面AB垂直放置，其中AB与“0”刻度线重合，O点落在“3”刻度线上，CD与“5”刻度线重合，若测得AB＝50cm，则CD的长是（ ）
A．30cmB．C．20cmD．
【分析】证明△COD∽△BOA，根据相似三角形的性质“相似三角形对应高的比等于相似比”列式计算即可求解．
【解答】解：根据题意得CD∥AB，
∴△COD∽△BOA，
∴，
∵AB＝50cm，
∴，
故选：B．
【点评】本题考查了相似三角形的判定和性质．熟练掌握相似三角形的判定和性质是关键．
9．（3分）已知线段a，b，c，求作线段x，使，下列作图中正确的是（ ）
A．B．
C．D．
【分析】利用图形得比例线段，再与已知式作对比，可以得出结论．
【解答】解：A、由图可得，即且x是所求线段，所以图形不能画出，故此选项不符合题意；
B、由图可得，即且x是所求线段，所以图形不能画出，故此选项不符合题意；
C、由图可得，即，所以图形不能画出，故此选项不符合题意；
D、由图可得，即，所以图形能画出，故此选项符合题意；
故选：D．
【点评】本题考查了比例线段，解题的关键是掌握比例线段的性质．
10．（3分）我们知道，除三角形外，其他多边形都不具有稳定性．如图，将正五边形OABCD的边AB固定，向右推动该正五边形，使得O为AD的中点，且点A，B，C，D在以点O为圆心的圆上，过点C作⊙O的切线EF，则∠BCF的度数为（ ）
A．18°B．30°C．36°D．54°
【分析】连接OC，OB，根据正五边形的性质得到∠BOC＝60°，根据等腰三角形的性质得到∠OCB＝∠OBC＝（180°﹣60°）＝60°，根据切线的性质得到∠OCF＝90°，于是得到结论．
【解答】解：连接OC，OB，
∵五边形OABCD的正五边形，
∴AB＝BC＝CD，
∴，
∵AD是⊙O的直径，
∴∠AOB＝∠COD＝∠BOC＝，
∵OC＝OB，
∴∠OCB＝∠OBC＝（180°﹣60°）＝60°，
∵点C作⊙O的切线EF，
∴∠OCF＝90°，
∴∠BCF＝90°﹣60°＝30°，
故选：B．
【点评】本题考查了正多边形与圆，切线的性质，三角形的内角和定理，等腰三角形的性质，正确地找出辅助线是解题的关键．
二.填空题（本大题共有6小题，每小题3分，共计18分．）
11．（3分）如果4a＝5b，那么＝ ．
【分析】先根据4a＝5b得到b＝a，再代入所求式子中求解即可．
【解答】解：∵4a＝5b，
∴，
∴．
故答案为：．
【点评】此题考查了比例的性质，熟练掌握比例的性质是解题的关键．
12．（3分）设a是方程2x2+x﹣1＝0的一个根，则3﹣4a2﹣2a的值为 1 ．
【分析】由a是方程2x2+x﹣1＝0的一个根，可得出2a2+a＝1，再将其代入原式＝3﹣2（2a2+a）中，即可求出结论．
【解答】解：∵a是方程2x2+x﹣1＝0的一个根，
∴2a2+a﹣1＝0，
∴2a2+a＝1，
∴原式＝3﹣2（2a2+a）＝3﹣2×1＝1．
故答案为：1．
【点评】本题主要考查一元二次方程的根以及代数式求值，牢记“把方程的解代入原方程，等式左右两边相等”是解题的关键．
13．（3分）已知圆锥的底面半径为2cm，母线长是4cm，则圆锥的侧面积是 8π cm2（结果保留π）．
【分析】圆锥的侧面积＝底面周长×母线长÷2．
【解答】解：底面圆的半径为2，则底面周长＝4π，侧面面积＝×4π×4＝8π（cm2）．
故答案为：8π．
【点评】本题利用了圆的周长公式和扇形面积公式求解．
14．（3分）如图，四边形ABCD内接于⊙O，E为DC延长线上一点．若∠BCE＝110°，则∠BOD的度数为 140° ．
【分析】根据邻补角的定义求出∠BCD，再根据圆周角定理计算即可．
【解答】解：∵∠BCE＝110°，
∴∠BCD＝180°﹣110°＝70°，
由圆周角定理得：∠BOD＝2∠BCD＝140°，
故答案为：140°．
【点评】本题考查的是圆内接四边形，掌握圆周角定理是解题的关键．
15．（3分）整式a2+b2﹣8a﹣2b+5的最小值为 ﹣12 ．
【分析】先分组，然后运用配方法得到（a﹣4）2+（b﹣1）2﹣12，最后利用偶次方的非负性得到最小值．
【解答】解：a2+b2﹣8a﹣2b+5，
＝a2﹣8a+b2﹣2b+5，
＝（a2﹣8a+16）+（b2﹣2b+1）+5﹣17，
＝（a﹣4）2+（b﹣1）2﹣12，
∵（a﹣4）2≥0，（b﹣1）2≥0，
∴当a＝4，b＝1时，原式有最小值，最小值为﹣12．
故答案为：﹣12．
【点评】本题考查配方法的应用和偶次方的非负性，正确运用该配方法是解答本题的关键．
16．（3分）如图，在等腰△ABC中，AB＝AC，点P在BA的延长线上，PA＝AB，点D在BC边上，PD＝PC，则的值是 ．
【分析】过点P作PE∥AC交DC延长线于点E，根据等腰三角形判定与性质，平行线的性质可证PB＝PE，再证△PCE≌△PDB，可得BD＝CE，再利用平行线分线段成比例的，结合线段的等量关系以及比例的性质即可得出结论．
【解答】解：如图，过点P作PE∥AC交DC延长线于点E，
∵AB＝AC，
∴∠B＝∠ACB，
∵AC∥PE，
∴∠ACB＝∠E，
∴∠B＝∠E，
∴PB＝PE，
∵PC＝PD，
∴∠PDC＝∠PCD，
∴∠BPD＝∠EPC，
∴在△PCE和△PDB中，
，
∴△PCE≌△PDB（SAS），
∴BD＝CE，
∵AC∥PE，
∴，
∵PA＝AB，
∴，
∴，
∴．
故答案为：．
【点评】本题考查了等腰三角形的判定与性质，平行线分线段成比例，以及全等三角形的判定，解决问题的关键是正确作出辅助线，列出比例式．
三、解答题（本大题共有10小题，共计72分．解答时应写出必要的文字说明、证明过程或演算步骤．）
17．（8分）解方程：
（1）5x2﹣3x＝x+1．
（2）3x（x﹣2）＝2（2﹣x）．
【分析】（1）先将一元二次根式变为一般形式，然后用公式法解方程即可；
（2）先移项，再用因式分解法解方程即可．
【解答】解：（1）原方程化为5x2﹣4x﹣1＝0，
∵a＝5，b＝﹣4，c＝﹣1，
∴Δ＝b2﹣4ac＝（﹣4）2﹣4×5×（﹣1）＝36＞0，
∴方程有两个不相等的实数根，
即x1＝1，；
（2）原方程可化为3x（x﹣2）+2（x﹣2）＝0，
∴（3x+2）（x﹣2）＝0，
∴x1＝2，．
【点评】本题主要考查了解一元二次方程，熟练掌握解一元二次方程的一般步骤是解题的关键．
18．（6分）已知关于x的一元二次方程x2+mx+2m﹣7＝0．
（1）求证：该方程总有两个不相等的实数根
（2）已知方程的一个根为x＝2，求m值及方程的另一根．
【分析】（1）根据题意只需要证明Δ＝m2﹣4（2m﹣7）＞0即可；
（2）一元二次方程的解是使方程左右两边相等的未知数的值，据此把x＝2代入原方程求出m的值，进而根据根与系数的关系求出另一个根即可．
【解答】（1）证明：∵关于x的一元二次方程x2+mx+2m﹣7＝0，
∴Δ＝m2﹣4（2m﹣7）
＝m2﹣8m+28
＝（m2﹣8m+16）+12
＝（m﹣4）2+12，
∵（m﹣4）2≥0，
∴（m﹣4）2+12＞0，
∴该方程总有两个不相等的实数根；
（2）解：把x＝2代入x2+mx+2m﹣7＝0得：22+2m+2m﹣7＝0，
解得，
∴原方程为，
设另一个根为x1，
∴，
∴，即另一个根为．
【点评】本题主要考查了一元二次方程根的判别式，根与系数的关系，一元二次方程的解的定义．
19．（6分）如图，在△ABC中，D，E分别是边AB，AC上的点，连接DE，且∠ADE＝∠ACB．
（1）求证：△ADE∽△ACB；
（2）若AD＝2DB，AE＝4，AC＝9，求BD的长．
【分析】（1）根据相似三角形的判定即可求出证．
（2）设BD＝x，则AD＝2x，AB＝3x，根据相似三角形的性质可知＝，从而列出方程解出x的值．
【解答】（1）证明：∵∠ADE＝∠ACB，∠A＝∠A，
∴△ADE∽△ACB；
（2）解：由（1）可知：△ADE∽△ACB，
∴＝，
设BD＝x，则AD＝2x，AB＝3x，
∵AE＝4，AC＝9，
∴＝，
解得：x＝（负值舍去），
∴BD的长是．
【点评】本题考查相似三角形，解题的关键是熟练运用相似三角形的性质与判定，本题属于中等题型．
20．（6分）如图，在坐标系中，A（1，6）、B（5，6）、C（7，4）．
（1）经过A、B、C三点的圆弧所在圆的圆心M的坐标为 （3，2） ；
（2）这个圆的半径为 ；
（3）直接判断点D（5，﹣3）与⊙M的位置关系．点D（5，﹣3）在⊙M 外 ．（填内、外、上）
【分析】（1）AB的垂直平分线所在直线为x＝2，可知圆心M在直线x＝3上，设M（3，m），根据MA＝MC，可求M点坐标；
（2）由（1）求出MA＝，即可求圆的半径；
（3）根据MD＝2＞，即可判断D点位置．
【解答】解：（1）∵A（1，6）、B（5，6），
∴AB的垂直平分线所在直线为x＝3，
∴圆心M在直线x＝3上，
设M（3，m），
∴MA＝MC，
∴4+（m﹣6）2＝16+（m﹣4）2，
解得m＝2，
∴M（3，2），
故答案为：（3，2）；
（2）∵M（3，2），
∴MA＝，
故答案为：；
（3）∵D（5，﹣3），M（3，2），
∴MD＝2＞，
∴点D（5，﹣3）在⊙M外，
故答案为：外．
【点评】本题考查三角形的外接圆与外心，熟练掌握同弧或等弧所对的圆周角相等，角平分线的性质是解题的关键．
21．（6分）智慧养老，让老年人享受数字经济红利．近年来，智慧养老成为老龄事业与产业发展的方向之一，广东省正致力于打造智慧养老的新标杆，为老年人提供更加贴心、高效的养老服务，同时为数字经济的发展注入新活力．某养老服务机构8月份为800名老人提供服务，10月份为1352名老人提供服务，求该机构9、10月份服务老人人数的月平均增长率．
【分析】根据题意列出方程，解方程，即可求解．
【解答】解：设该机构两个月平均增长率为x．根据题意得：
（1+x）2＝，
解得x1＝0.3，x2＝﹣2.3 （不合题意，舍去）．
答：该机构9、10月份服务老人人数的月平均增长率为30%．
【点评】本题考查了一元二次方程的应用，理解题意是关键．
22．（6分）学完图形变换后，小宛以“正五边形的变换”为主题开展探究活动：
（1）如图1，将正五边形纸片ABCDE折叠，使点B与点E重合，折痕为AM，展开后，再将纸片折叠，使边AB落在线段AM上，点B的对应点为点B，折痕为AF，求∠AFB的大小．
（2）如图2，用一些全等的正五边形按图示方式拼接，使相邻的两个正五边形有公共顶点，所夹的锐角为24°，图中所示的是前3个正五边形拼接的情况，若拼接一圈后，中间能形成一个正多边形，请直接写出这个正多边形的边数．
【分析】（1）根据正五边形的性质，翻折的性质以及三角形内角和定理进行计算即可；
（2）根据拼图和周角的定义求出正多边形的一个内角的度数，进而求出外角的度数，再根据外角和是360°确定正多边形的边数．
【解答】解：（1）如图1，∵五边形ABCDE是正五边形，
∴∠BAE＝∠B＝＝108°，
由题意可知，AM所在的直线是正五边形的对称轴，
∴∠BAM＝∠EAM＝∠BAE＝54°，
由翻折的性质可知，
∠BAF＝∠B′AF＝∠BAM＝27°，
∴∠AFB＝180°﹣108°﹣27°＝45°；
（2）由题意可知，所得到的正多边形的一个内角的度数为360°﹣108°﹣108°﹣24°＝120°，
则这个正多边形的外角为180°﹣120°＝60°，
所以这个正多边形的边数为＝6，
即这个正多边形是正六边形．
【点评】本题考查正多边形和圆，翻折的性质，掌握正五边形的性质，翻折的性质以及正多边形的外角和是360°是正确解答的关键．
23．（8分）在Rt△AFD中，∠F＝90°，点B、C分别在AD、FD上，以AB为直径的半圆O过点C，连接AC，将△AFC沿AC翻折得△AEC，且点E恰好落在直径AB上．
（1）判断：直线FC与半圆O的位置关系是 相切 ；并证明你的结论．
（2）若OB＝BD＝2，求CE的长．
【分析】（1）根据切线的判定定理证明∠F＝∠OCD＝90°，即可得出FC与⊙O相切；
（2）利用∠COD＝60°，得出CE＝OC•sin∠COD进而求出．
【解答】解：（1）直线FC与⊙O的位置关系是相切；
证明：连接OC
∵OA＝OC，∴∠1＝∠2，
由翻折得，∠1＝∠3，∠F＝∠AEC＝90°
∴∠3＝∠2，
∴OC∥AF，
∴∠F＝∠OCD＝90°，
∴FC与⊙O相切；
（2）在Rt△OCD中，cs∠COD＝
∴∠COD＝60°，
在Rt△OCD中，CE＝OC•sin∠COD＝．
【点评】此题主要考查了直线与圆的位置关系以及解直角三角形等知识，切线的判定定理是初中阶段最重要的定理之一同学们应熟练掌握．
24．（8分）
【分析】初步应用：设剪去小正方形的边长为x cm，则折成的无盖长方体储物盒的底面为长（50﹣2x）cm，宽为（40﹣2x）cm的矩形，根据储物盒的底面积是816cm2，可列出关于x的一元二次方程，解之可得出x的值，再将其符合题意的值代入816x中，即可求出结论；
储物收纳：设ME＝y cm，则折成的有盖的长方体储物盒的底面为长（50﹣y）cm，宽为（40﹣2y）cm的矩形，根据储物盒的底面积为800cm2，可列出关于y的一元二次方程，解之可得出y的值（即折成的有盖的长方体储物盒的高），取其符合题意的值代入（50﹣y）及（40﹣2y）中，可得出折成的有盖的长方体储物盒的长及宽，再对比玩具攀爬小火车的尺寸，即可得出结论．
【解答】解：初步应用：设剪去小正方形的边长为x cm，则折成的无盖长方体储物盒的底面为长（50﹣2x）cm，宽为（40﹣2x）cm的矩形，
根据题意得：（50﹣2x）（40﹣2x）＝816，
整理得：x2﹣45x+296＝0，
解得：x1＝8，x2＝37（不符合题意，舍去），
∴816x＝816×8＝6528．
答：这个储物盒的容积为6528cm3；
储物收纳：设ME＝y cm，则折成的有盖的长方体储物盒的底面为长＝（50﹣y）cm，宽为（40﹣2y）cm的矩形，
根据题意得：（50﹣y）（40﹣2y）＝800，
整理得：y2﹣70y+600＝0，
解得：y1＝10，y2＝60（不符合题意，舍去），
∴50﹣y＝50﹣10＝40，40﹣2y＝40﹣2×10＝20，
∴折成的有盖的长方体储物盒的长为40cm，宽为20cm，高为10cm．
又∵40＞35，20＞15，10＜16，
∴这个玩具不能完全放入该储物盒．
【点评】本题考查了一元二次方程的应用，找准等量关系，正确列出一元二次方程是解题的关键．
25．（9分）如图，已知∠PAQ及AP边上一点C．
（1）尺规作图：（保留作图痕迹，不写作法）
①作⊙O，使得圆心O在射线AQ上，且⊙O经过A、C两点，交射线AQ于点B；
②在射线CP上求作点M，使点M到点C的距离与点M到射线AQ的距离相等；
（2）在（1）的条件下，若AC＝4，AB＝5，直接写出OM的长＝ ．
【分析】（1）作AC的垂直平分线交AQ于点O．
（2）作AC的垂直平分线交AQ于点O，以点O为圆心，OC为半径画圆交AQ于点B，作∠CBQ的角平分线交AP于点M，点M即为所求；
（3）根据三角形相似是性质和勾股定理求解．
【解答】解：（1）①⊙O即为所求；
②点M即为所求；
（2）过点M作MH⊥AQ于点H，
∵AB为直径，
∴∠ACB＝90°，
∴BC＝＝3，
∵∠BAC＝∠MAH，∴△BAC∽△MAN，
∴＝，即：，
解得：MH＝6，AH＝8，
∴OH＝AH﹣AO＝5.5，
在Rt△OHM中，OM＝＝，
故答案为：．
【点评】本题考查了复杂作图，掌握线段的垂直平分线的性质、勾股定理、相似三角形的性质是解题的关键．
26．（9分）“关联”是解决数学问题的重要思维方式．角平分线的有关联想就有很多…
【问题提出】
（1）如图①，PC是△PAB的角平分线，求证：．
请根据小明或小红的思路，选择一种并完成证明．
【尝试应用】
（2）如图②，在Rt△ABC中，∠ACB＝90°，D是边AB上一点，连结CD，将△ACD沿CD所在直线折叠，使点A恰好落在边BC的中点E处．若DE＝5，求AC的长．
【拓展提高】
（3）如图③，△ABC中，AB＝6，AC＝4，AD为∠BAC的角平分线．AD的垂直平分线EF交BC延长线于点F，连接AF，当BD＝3时，AF的长为 6 ．
【分析】（1）选择小明的思路：过点BD∥AP交PC的延长线于点D，证明△ACP∽△BCD，列出比例式，根据角平分线的定义即可得证；选择小红的思路：过点C分别作CD⊥PA交PA于点D，作CE⊥PB交PB于点E，作PF⊥BC于点F，根据角平分线的性质及三角形的面积公式，即可得证；
（2）根据折叠的性质求出AB，BC，利用勾股定理即可解答；
（3）根据角平分线的性质及线段垂直平分线的性质，证明△FBA∽△FAC，列出比例式，即可解答．
【解答】（1）证明：选择小明的思路：
如图，过点BD∥AP交PC的延长线于点D，
∵BD∥AP，
∴∠APC＝∠D，
又∵∠ACP＝∠BCD，
∴△ACP∽△BCD，
∴，
∵PC是△PAB的角平分线，
∴∠APC＝∠BPC，
∴∠BPC＝∠D，
∴PB＝BD，
∴；
选择小红的思路：
如图，过点C分别作CD⊥PA交PA于点D，作CE⊥PB交PB于点E，作PF⊥BC于点F，
∵PC是△PAB的角平分线，
∴CD＝CE，
∴，，，，
∴BC•PF＝PB•CE，PA•CD＝AC•PF，
∴，
∴，
∴；
（2）解：由折叠知AD＝DE＝5，CE＝AC，
∵点E是BC的中点，
∴BC＝2CE＝2AC，
由折叠知CD是∠ACB的角平分线，
∴，
∴，
∴BD＝2AD＝10，
∴AB＝AD+BD＝15，
在Rt△ABC中，AC2+BC2＝AB2，
∴AC2+（2AC）2＝152，
∴；
（3）解：∵AD为∠BAC的角平分线，
∴，∠BAD＝∠DAC，
∵△ABC中，AB＝6，AC＝4，BD＝3，
∴，
∴CD＝2，
∵AD的垂直平分线EF交BC延长线于F，
∴AF＝DF，
∴∠FAD＝∠FDA，
∵∠FAD＝∠FAC+∠DAC，∠FDA＝∠B+∠BAD，
∴∠B＝∠FAC，
∵∠AFB＝∠CFA，
∴△FBA∽△FAC，
∴，
∴，
∴AF＝6，
故答案为：6．
【点评】本题考查相似形综合应用，主要考查相似三角形的判定与性质，三角形的面积，角平分线的定义，勾股定理，掌握相似三角形的判定与性质是解题的关键．
如何利用闲置纸板箱制作储物盒
准备素材
小明收集到闲置纸板箱如图①所示．将其拆解出的如图②和图③两种矩形纸板，两种纸板的长和宽如图所示．
设计方案
小明分别将图②和图③两种矩形纸板以不同的方式制作储物盒．
图②矩形纸板的制作方式
图③矩形纸板的制作方式
如图④，裁去纸板角上4个相同的小正方形，折成一个无盖长方体储物盒．
如图⑤，将纸板四个角裁去4个相同的小矩形，折成一个有盖的长方体储物盒．
目标达成
小明利用两种不同的制作方式进一步探究．
初步应用
小明按照矩形纸板②的制作方式，制作了如图④所示的储物盒的底面积是816cm2，求这个储物盒的容积．
储物收纳
小明按照矩形纸板③的制作方式，制作了如图⑤所示储物盒，若EF和HG两边恰好重合且无重叠部分，盒子的底面积为800cm2．小明家里一个玩具攀爬小火车的实物图和尺寸大小如图⑥所示，通过计算判断这个玩具能否完全放入该储物盒．

小明思路：关联“平行线、等腰三角形”，过点B作BD∥PA，交PC的延长线于点D，利用“三角形相似”．
小红思路：关联“角平分线上的点到角的两边的距离相等”，过点C分别作CD⊥PA交PA于点D，作CE⊥PB交PB于点E，利用“等面积法”．
如何利用闲置纸板箱制作储物盒
准备素材
小明收集到闲置纸板箱如图①所示．将其拆解出的如图②和图③两种矩形纸板，两种纸板的长和宽如图所示．
设计方案
小明分别将图②和图③两种矩形纸板以不同的方式制作储物盒．
图②矩形纸板的制作方式
图③矩形纸板的制作方式
如图④，裁去纸板角上4个相同的小正方形，折成一个无盖长方体储物盒．
如图⑤，将纸板四个角裁去4个相同的小矩形，折成一个有盖的长方体储物盒．
目标达成
小明利用两种不同的制作方式进一步探究．
初步应用
小明按照矩形纸板②的制作方式，制作了如图④所示的储物盒的底面积是816cm2，求这个储物盒的容积．
储物收纳
小明按照矩形纸板③的制作方式，制作了如图⑤所示储物盒，若EF和HG两边恰好重合且无重叠部分，盒子的底面积为800cm2．小明家里一个玩具攀爬小火车的实物图和尺寸大小如图⑥所示，通过计算判断这个玩具能否完全放入该储物盒．

小明思路：关联“平行线、等腰三角形”，过点B作BD∥PA，交PC的延长线于点D，利用“三角形相似”．
小红思路：关联“角平分线上的点到角的两边的距离相等”，过点C分别作CD⊥PA交PA于点D，作CE⊥PB交PB于点E，利用“等面积法”．