四川省资阳市安岳县四川省安岳中学2024-2025学年九年级上学期11月期中数学试题

这是一份四川省资阳市安岳县四川省安岳中学2024-2025学年九年级上学期11月期中数学试题，共10页。试卷主要包含了1m）．，7米等内容，欢迎下载使用。
注意事项：
1.答卷前考生务必把自己的姓名、准考证号填写在答题卡上。
2.回答选择题时用2B铅笔将答题卡上对应题目的答案标号涂黑；回答非选择题时，用0.5毫米黑色墨迹签字笔将答案写在答题卡上，写在本试卷上无效。
3.试卷满分150分，考试时间120分钟，考试结束后将本试卷和答题卡一并交回。
第I卷（选择题）
一、单选题（共40分）
1．（本题4分）下列计算正确的是（ ）
A．B．
C．D．
2．（本题4分）要使式子有意义，则x的取值范围是（ ）
A．B．C．D．
3．（本题4分）下列二次根式与不是同类二次根式的是（ ）
A．B．C．D．
4．（本题4分）如图，在中，点D， E分别在边 ， 上，且， 若 ， 的面积是 2，则的面积是( )
A．3B．4C．8D．
5．（本题4分）在平面直角坐标系中，将点向右平移个单位，再向下平移个单位，得到的点的坐标为（ ）
A．B．C．D．
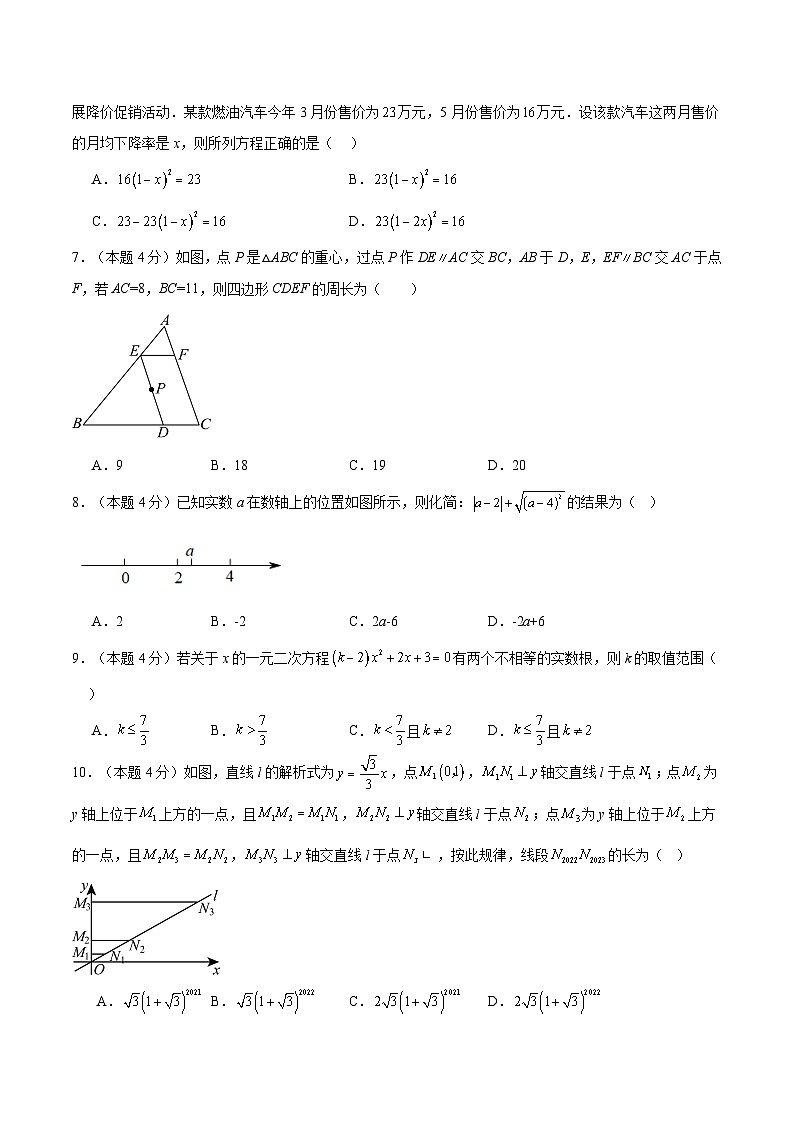
6．（本题4分）近年来，由于新能源汽车的崛起，燃油汽车的销量出现了不同程度的下滑，经销商纷纷开展降价促销活动．某款燃油汽车今年3月份售价为万元，5月份售价为万元．设该款汽车这两月售价的月均下降率是x，则所列方程正确的是（ ）
A．B．
C．D．
7．（本题4分）如图，点P是△ABC的重心，过点P作DEAC交BC，AB于D，E，EFBC交AC于点F，若AC=8，BC=11，则四边形CDEF的周长为（ ）
A．9B．18C．19D．20
8．（本题4分）已知实数a在数轴上的位置如图所示，则化简：的结果为（ ）
A．2B．-2C．2a-6D．-2a+6
9．（本题4分）若关于x的一元二次方程有两个不相等的实数根，则k的取值范围（ ）
A．B．C．且D．且
10．（本题4分）如图，直线l的解析式为，点，轴交直线l于点；点为y轴上位于上方的一点，且，轴交直线l于点；点为y轴上位于上方的一点，且，轴交直线l于点，按此规律，线段的长为（ ）
A．B．C．D．
第II卷（非选择题）
二、填空题（共24分）
11．（本题4分）使代数式有意义的x的取值范围是 ．
12．（本题4分）当时，代数式的值是 ．
13．（本题4分）已知一元二次方程有两个相等的实数根，则k的值是 ．
14．（本题4分）实数在数轴上的位置如图所示，化简=
15．（本题4分）工人师傅童威准备在一块长为60，宽为48的长方形花圃内修建四条宽度相等，且与各边垂直的小路．四条小路围成的中间部分恰好是一个正方形，且边长是小路宽度的8倍．若四条小路所占面积为160．设小路的宽度为x，依题意列方程，化为一般形式为
16．（本题4分）如图，在矩形ABCD中，AB=6cm，BC=9cm，点E，F分别在边AB，BC上，AE=2cm，BD，EF交于点G，若G是EF的中点，则BG的长为 cm．
三、解答题（共86分）
17．（本题12分）（1）计算：
（2）解方程：
18．（本题8分） 先化简，再求值：÷（-m-1）其中m是方程m2-4m-12=0的根．
19．（本题8分）已知是方程的两根，在不解方程的前提下，求下列各式的值．
(1) (2)
20．（本题8分）（1）计算：；
（2）若，求的值．
21．（本题8分）阅读例题，解答问题：
例：解方程．
解：原方程化为．
令，原方程化成
解得，（不合题意，舍去）．
．．
∴原方程的解是，
请模仿上面的方法解方程：．
22．（本题8分）如图，某数学兴趣小组想测量一棵树CD的高度，他们先在点A处测得树顶C的仰角为30°，然后沿AD方向前行10m，到达B点，在B处测得树顶C的仰角高度为60°（A、B、D三点在同一直线上）．请你根据他们测量数据计算这棵树CD的高度（结果精确到0.1m）．（参考数据：≈1.414，≈1.732）
23．（本题10分）定义：已知是关于x的一元二次方程的两个实数根，若，且，则称这个方程为“限根方程”．如：一元二次方程的两根为，因，，所以一元二次方程为“限根方程”．
请阅读以上材料，回答下列问题：
(1)判断一元二次方程是否为“限根方程”，并说明理由；
(2)若关于x的一元二次方程是“限根方程”，且两根满足，求k的值；
(3)若关于x的一元二次方程是“限根方程”，求m的取值范围．
24．（本题12分）某商场销售一批名牌衬衫，平均每天可售出20件，每件可盈利40元．为了扩大销售量，增加盈利，尽快减少库存，商场采取适当的降价措施．经调查发现，如果每件降价1元，商场平均每天可多售出2件．
（1）若商场平均每天要盈利1200元，每件衬衫应降价多少元？
（2）该商场平均每天盈利能达到1500元吗？如果能，求出此时应降价多少；如果不能，请说明理由；
（3）该商场平均每天盈利最多多少元？达到最大值时应降价多少元？
25．（本题12分）如图1，在等边中，，点D，E分别在边上，，连接，点M，P，N分别为的中点．

（1）观察猜想：图1中，线段与的数量关系是 ， ；
（2）探究证明：把绕点A逆时针方向旋转到图2的位置，连接，则上面题（1）中的两个结论是否依然成立，并说明理由；
（3）拓展延伸：把绕点A在平面内自由旋转，若，请直接写出周长的最大值
参考答案：
11．
12．2017
13．4
14．a.
15．16x2+108x-160=0．
16．
17．（1）；（2），
18．，．
19．(1)
(2)
20．（1）；（2）4
21．，
22．这棵树CD的高度为8.7米
23．（1）解：，
，
∴或，
∴．
∵，，
∴此方程为“限根方程”；
（2）∵方程的两个根分比为，
∴， ．
∵，
∴，
解得：，．
分类讨论：①当时，原方程为，
∴，，
∴，，
∴此时方程是“限根方程”，
∴符合题意；
②当时，原方程为，
∴，，
∴，，
∴此时方程不是“限根方程”，
∴不符合题意．
综上可知k的值为2；
（3），
，
∴或，
∴或．
∵此方程为“限根方程”，
∴此方程有两个不相等的实数根，
∴，且，
∴，即，
∴且．
分类讨论：①当时，
∴，
∵，
∴，
解得：；
②当时，
∴，
∵，
∴，
解得：．
综上所述，m的取值范围为或．
24．解：（1）设每件衬衫应降价元，则每件盈利元，每天可以售出，
由题意，得，
即：，
解，得，，
为了扩大销售量，增加盈利，尽快减少库存，所以的值应为20，
所以，若商场平均每天要盈利1200元，每件衬衫应降价20元；
（2）假设能达到，由题意，得，
整理，得，
，
即：该方程无解，
所以，商场平均每天盈利不能达到1500元；
（3）设商场平均每天盈利元，每件衬衫应降价元，
由题意，得，
，
，
，
当元时，该函数取得最大值为1250元，
所以，商场平均每天盈利最多1250元，达到最大值时应降价15元．
25．解：（1）∵△ABC是等边三角形，
∴AB=AC，∠A=60°，
∵AD=AE，
∴AB-AD=AC-AE，即BD=CE，
∵M，P，N分别是DE，DC，BC的中点，
∴MP=EC，PM∥EC，PN=BD，PN∥BD，
∴PM=PN，∠MPD=∠ACD，∠NPD=∠ADC，
在△ACD中，∠ADC+∠ACD=180°-∠A=120°，
∴∠MPN=∠MPD+∠NPD=120°．
故答案为：PM=PN，120°；
（2）成立，理由如下：
∵AB=AC，AD=AE，∠BAC=∠DAE=60°，∠ABC=∠ACB=60°，
∴∠BAD=∠CAE，
∵AB=AC，∠BAD=∠CAE，AD=AE，
∴△ABD≌△ACE（SAS），
∴BD=CE，
∵DM=ME，DP=PC，BN=NC，
∴MP=EC，PM∥EC，PN=BD，PN∥BD，
∴MP=PN，
∴△PMN是等腰三角形．
∵PM∥CE，
∴∠DPM=∠DCE，
∵PN∥BD，
∴∠PNC=∠DBC，
∵∠DPN=∠DCB+∠PNC=∠DCB+∠DBC，
∴∠MPN=∠DPM+∠DPN=∠DCE+∠DCB+∠DBC=∠BCE+∠DBC=∠ACB+∠ACE+∠DBC=∠ACB+∠ABD+∠DBC=∠ACB+∠ABC，
∵∠BAC=60°，
∴∠ACB+∠ABC=120°，
∴∠MPN=120°，
∴PM=PN，∠MPN=120°；
（3）由（2）知：PM=PN，∠MPN=120°，
∵BD≤AB+AD，
∴BD≤14，
∴点D恰好在BA延长线上时，BD、CE取得最大值，且最大值为14，
∴PM 、PN的最大值为7，
此时MN经过点A，即MN垂直平分BC，如图：
∵△ABC、△ADE是等边三角形，且AD=4，AB=10，
∴∠BAN=∠DAM=30°，
∴BN=CN=5，DM=EM=2，
∴AN=5，AM=2，
∴△PMN周长的最大值为PM+PN+MN=7+7+5+2=14+7．
题号
1
2
3
4
5
6
7
8
9
10
答案
C
C
D
D
A
B
B
A
C
C