模块四 题型全通关专题3 解答型题型第3讲 证明题 -最新中考数学二轮专题复习训练（含解析）

这是一份模块四 题型全通关专题3 解答型题型第3讲 证明题 -最新中考数学二轮专题复习训练（含解析），共48页。
第3讲 证明题
推理能力是初中数学的核心素养之一，推理能力主要是从一些事实和命题出地，依据规则推出其他命题或结论的能力．理解逻辑推理在形成数学概念、法则、定理和解决问题中的重要性，初步掌握推理的基本形式和规则；对于一些简单问题，能通过特殊结果推断一般结论；理解命题的结构与联系，探索并表述认证过程．推理能力有助于逐步养成重论据、合乎逻辑的思维习惯，形成实事求是的科学态度与理性精神．
考点讲解：题目以已知、求证的方式给出，题设和结论明确，考生需要给出完整的证明．证明采用“∵、∴”的形式展开，重要步骤可以写出理论依据．证明所用的条件必须是已知或者前面被证明的结论．
【例1】
（2023·四川攀枝花·统考中考真题）
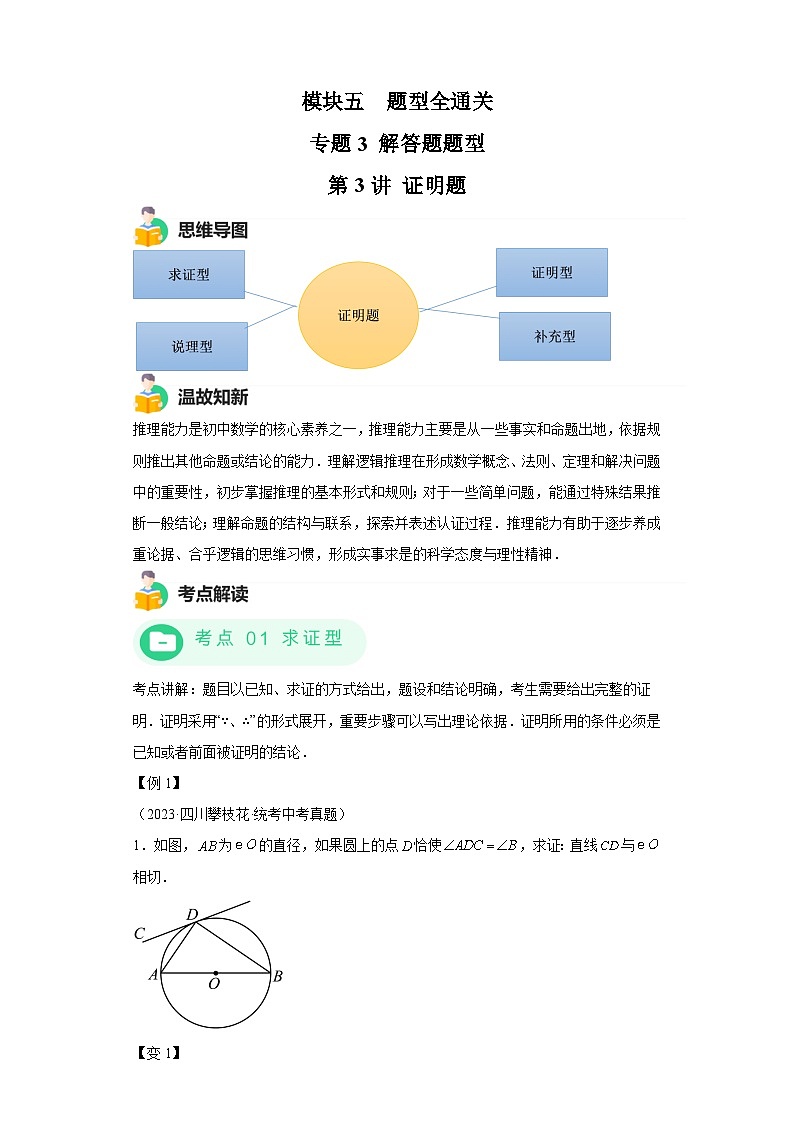
1．如图，为的直径，如果圆上的点恰使，求证：直线与相切．

【变1】
（2023·江苏镇江·统考中考真题）
2．如图，B是AC的中点，点D，E在同侧，，．
(1)求证：≌．
(2)连接，求证：四边形是平行四边形．
考点讲解：题目以“证明”的形式给出，题设和结论有时没有直接给出，需要先辨析清楚，有时还需要画出图形，结合图形写出已知和求证，然后再证明．
【例1】
（2023·北京·统考中考真题）
3．在中、，于点M，D是线段上的动点（不与点M，C重合），将线段绕点D顺时针旋转得到线段．

(1)如图1，当点E在线段上时，求证：D是的中点；
(2)如图2，若在线段上存在点F（不与点B，M重合）满足，连接，，直接写出的大小，并证明．
【变1】
（2023·湖南娄底·统考中考真题）
4．如图1，点为等边的重心，点为边的中点，连接并延长至点，使得，连接，，，

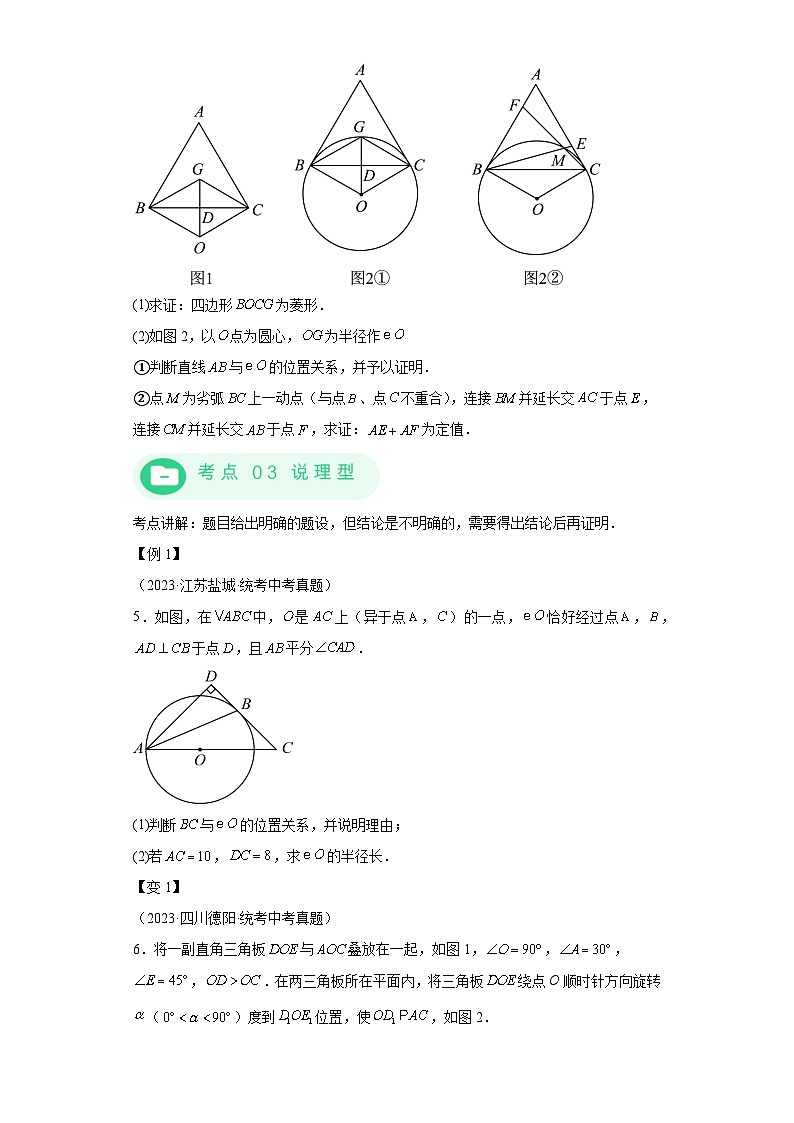
(1)求证：四边形为菱形．
(2)如图2，以点为圆心，为半径作
①判断直线与的位置关系，并予以证明．
②点为劣弧上一动点（与点、点不重合），连接并延长交于点，连接并延长交于点，求证：为定值．
考点讲解：题目给出明确的题设，但结论是不明确的，需要得出结论后再证明．
【例1】
（2023·江苏盐城·统考中考真题）
5．如图，在中，是上（异于点，）的一点，恰好经过点，，于点，且平分．

(1)判断与的位置关系，并说明理由；
(2)若，，求的半径长．
【变1】
（2023·四川德阳·统考中考真题）
6．将一副直角三角板与叠放在一起，如图1，，，，．在两三角板所在平面内，将三角板绕点O顺时针方向旋转（）度到位置，使，如图2．

(1)求的值；
(2)如图3，继续将三角板绕点O顺时针方向旋转，使点E落在边上点处，点D落在点处．设交于点G，交于点H，若点G是的中点，试判断四边形的形状，并说明理由．
考点讲解：一种形式是题目以填空的形式给出，题设和结论明确，证明结构确定，需要考生读懂证明过程，按照给定的证明结构完善证明过程．考生不能按照自己的想法另起炉灶．第二种形式是题目给出完整的证明过程，找出证明过程中的错误，再写出正确的证明过程．第三种形式是题目给定一些关系，从中选择一部分作为题设，一个作为结论，构造真命题后再证明．
【例1】
（2023·浙江衢州·统考中考真题）
7．已知：如图，在和中，在同一条直线上．下面四个条件：①；②；③；④．

(1)请选择其中的三个条件，使得（写出一种情况即可）；
(2)在（1）的条件下，求证：．
【变1】
（2023·重庆·统考中考真题）
8．学习了平行四边形后，小虹进行了拓展性研究．她发现，如果作平行四边形一条对角线的垂直平分线，那么这个平行四边形的一组对边截垂直平分线所得的线段被垂足平分． 她的解决思路是通过证明对应线段所在的两个三角形全等得出结论．请根据她的思路完成以下作图与填空：
用直尺和圆规，作的垂直平分线交于点E，交于点F，垂足为点O．（只保留作图痕迹）

已知：如图，四边形是平行四边形，是对角线，垂直平分，垂足为点O．
求证：．
证明：∵四边形是平行四边形，
∴．
∴ ① ．
∵垂直平分，
∴ ② ．
又___________③ ．
∴．
∴．
小虹再进一步研究发现，过平行四边形对角线中点的直线与平行四边形一组对边相交形成的线段均有此特征．请你依照题意完成下面命题：
过平行四边形对角线中点的直线 ④ ．
（2023·山东青岛·统考中考真题）
9．如图，在中，的平分线交于点E，的平分线交于点F，点G，H分别是和的中点．

(1)求证：；
(2)连接．若，请判断四边形的形状，并证明你的结论．
（2023·江苏南通·统考中考真题）
10．如图，点，分别在，上，，，相交于点，．
求证：．
小虎同学的证明过程如下：
证明：∵，
∴．
∵，
∴．第一步
又，，
∴第二步
∴第三步

(1)小虎同学的证明过程中，第___________步出现错误；
(2)请写出正确的证明过程．
（2023·湖南湘西·统考中考真题）
11．如图，四边形是平行四边形，，且分别交对角线于点M，N，连接．

(1)求证：；
(2)若．求证：四边形是菱形．
（2023·江苏宿迁·统考中考真题）
12．（1）如图，是的直径，与交于点F，弦平分，点E在上，连接、，________．求证：________．

从①与相切；②中选择一个作为已知条件，余下的一个作为结论，将题目补充完整（填写序号），并完成证明过程．
（2）在（1）的前提下，若，，求阴影部分的面积．
（2023·山东泰安·统考中考真题）
13．如图，、是两个等腰直角三角形，．

(1)当时，求；
(2)求证：；
(3)求证：．
（2023·山东泰安·统考中考真题）
14．如图，矩形中，对角线相交于点O，点F是边上的一点，连接，将沿直线折叠，点D落在点G处，连接并延长交于点H，连接并延长交于点M，交的延长线于点E，且．

(1)求证：四边形是平行四边形；
(2)求证：．
（2023·山东·统考中考真题）
15．已知：射线平分为上一点，交射线于点，交射线于点，连接．

(1)如图1，若，试判断四边形的形状，并说明理由；
(2)如图2，过点作，交于点；过点作，交于点．求证：．
（2023·甘肃兰州·统考中考真题）
16．如图，内接于，是的直径，，于点，交于点，交于点，，连接．

(1)求证：是的切线；
(2)判断的形状，并说明理由；
(3)当时，求的长．
（2023·山东东营·统考中考真题）
17．（1）用数学的眼光观察．
如图，在四边形中，，是对角线的中点，是的中点，是的中点，求证：．
（2）用数学的思维思考．
如图，延长图中的线段交的延长线于点，延长线段交的延长线于点，求证：．
（3）用数学的语言表达．
如图，在中，，点在上，，是的中点，是的中点，连接并延长，与的延长线交于点，连接，若，试判断的形状，并进行证明．
（2023·江苏泰州·统考中考真题）
18．如图，矩形是一张纸，其中，小天用该纸玩折纸游戏．
游戏1 折出对角线，将点B翻折到上的点E处，折痕交于点G．展开后得到图①，发现点F恰为的中点．
游戏2 在游戏1的基础上，将点C翻折到上，折痕为；展开后将点B沿过点F的直线翻折到上的点H处；再展开并连接后得到图②，发现是一个特定的角．
(1)请你证明游戏1中发现的结论；
(2)请你猜想游戏2中的度数，并说明理由．
（2023·湖北恩施·统考中考真题）
19．如图，在矩形中，点是的中点，将矩形沿所在的直线折叠，的对应点分别为，，连接交于点．

(1)若，求的度数；
(2)连接EF，试判断四边形的形状，并说明理由．
．（2023·内蒙古·统考中考真题）
20．如图，在菱形中，对角线相交于点，点分别是边，线段上的点，连接与相交于点．

(1)如图1，连接．当时，试判断点是否在线段的垂直平分线上，并说明理由；
(2)如图2，若，且，
①求证：；
②当时，设，求的长（用含的代数式表示）．
（2023·四川攀枝花·统考中考真题）
21．如图1，在中，，沿方向向左平移得到，A、对应点分别是、．点是线段上的一个动点，连接，将线段绕点A逆时针旋转至线段，使得，连接．

(1)当点与点重合时，求的长；
(2)如图2，连接、．在点的运动过程中：
①和是否总是相等？若是，请你证明；若不是，请说明理由；
②当的长为多少时，能构成等腰三角形？
（2023·江苏泰州·统考中考真题）
22．已知：A、B为圆上两定点，点C在该圆上，为所对的圆周角．

知识回顾
(1)如图①，中，B、C位于直线异侧，．
①求的度数；
②若的半径为5，，求的长；
逆向思考
(2)如图②，P为圆内一点，且，，．求证：P为该圆的圆心；
拓展应用
(3)如图③，在（2）的条件下，若，点C在位于直线上方部分的圆弧上运动．点D在上，满足的所有点D中，必有一个点的位置始终不变．请证明．
参考答案：
1．见详解
【分析】由等腰三角形的性质和圆周角定理得出，则，再由切线的判定即可得出结论．
【详解】证明：如图，连接，
，
，
为的直径，
，
，
，
，
即，
，
是的半径，
直线与相切．

【点睛】本题考查了切线的判定、圆周角定理、直角三角形的性质、等腰三角形的性质等知识；熟练掌握圆周角定理和切线的判定是解题的关键．
2．(1)见解析
(2)见解析
【分析】（1）由B是的中点得，结合，，根据全等三角形的判定定理“”即可证明≌；
（2）由（1）中≌得，进一步得，再结合，根据一组对边平行且相等的四边形是平行四边形即可证明．
【详解】（1）解：∵B是的中点，
∴．
在和中，
∴≌（）．
（2）如图所示，
∵≌，
∴，
∴．
又∵，
∴四边形是平行四边形．
【点睛】本题考查了全等三角形的判定与性质、平行四边形的判定，熟练掌握全等三角形的判定方法与性质是解题的关键．
3．(1)见解析
(2)，证明见解析
【分析】（1）由旋转的性质得，，利用三角形外角的性质求出，可得，等量代换得到即可；
（2）延长到H使，连接，，可得是的中位线，然后求出，设，，求出，证明，得到，再根据等腰三角形三线合一证明即可．
【详解】（1）证明：由旋转的性质得：，，
∵，
∴，
∴，
∴，
∴，即D是的中点；
（2）；
证明：如图2，延长到H使，连接，，
∵，
∴是的中位线，
∴，，
由旋转的性质得：，，
∴，
∵，
∴，是等腰三角形，
∴，，
设，，则，，
∴，
∴，
∵，
∴，
∴，
∴，
在和中，，
∴，
∴，
∵，
∴，即．

【点睛】本题考查了等腰三角形的判定和性质，旋转的性质，三角形外角的性质，三角形中位线定理以及全等三角形的判定和性质等知识，作出合适的辅助线，构造出全等三角形是解题的关键．
4．(1)见解析；
(2)①直线是的切线；②见解析．
【分析】（1）如图1，延长交于点，连接，由是等边三角形，是重心，点为边的中点，得⟂，，进而证明四边形是平行四边形，于是即可得四边形为菱形；
（2）①延长交于点，连接，先证为的角平分线，进而求得，又由菱形的性质得，从而有，于是根据切线的判定即可得出结论；②在优弧上取一点，连接、，由①得，进而求得，再由圆内接四边形的性质求得，从而根据角的和差关系求得，于是证明得，即可证明结论成立．
【详解】（1）证明：如图，延长交于点，连接，

∵是等边三角形，是重心，点为边的中点，
∴中线过点，即、、三点共线，，，
∴⟂，，
∵，
∴四边形是平行四边形，
∵⟂，
∴四边形为菱形；
（2）①解：直线是的切线，理由如下：延长交于点，连接，

∵是等边三角形，是重心，点为边的中点，
∴中线过点，即、、三点共线，，，，
∴为的角平分线，
∴，
∵四边形是菱形，
∴，
∴，
∴，
∴直线是的切线；
②证明：在优弧上取一点，连接、，

由①得，
∵，
∴，
∴，
∴，
∵四边形内接于，
∴，
∴，
∵，
∴，
∴，
∵，，
∴
∴
∵
∴，即为定值．
【点睛】本题主要考查了全等三角形的判定及性质，等边三角形的性质，重心的性质，切线的判定以及菱形的判定，熟练掌握菱形的判定，全等三角形的判定及性质，等边三角形的性质，重心的性质以及切线的判定定理是解题的关键．
5．(1)见解析
(2)的半径长为．
【分析】（1）连接，证明，即可证得，从而证得是圆的切线；
（2）设，则，利用勾股定理求得，推出，利用相似三角形的性质列得比例式，据此求解即可．
【详解】（1）证明：连接，如下图所示，

∵是的平分线，
∴，
又∵，
∴，
∴，
∴，
∴，即，
又∵过半径的外端点B，
∴与相切；
（2）解：设，则，
∵在中，，，，
∴，
∵，
∴，
∴，即，
解得．
故的半径长为．
【点睛】本题考查了切线的判定，相似三角形的判定和性质，以及勾股定理，熟练掌握切线的判定是解本题的关键．
6．(1)
(2)正方形，见解析
【分析】（1）确定旋转角，结合，，计算即可．
（2）先证明四边形是矩形，再利用等腰直角三角形的性质，结合一组邻边相等的矩形是正方形证明即可．
【详解】（1）根据题意，得旋转角，
∵，，
∴，
故．
（2）根据题意，得旋转角，
∵，，
∴，
∵，，
∴，，
∴，
∵，，

∴，
∴，
∴，
∴四边形是矩形，
∵，
∴四边形是正方形．
【点睛】本题考查了旋转的性质，矩形的判断，正方形的判断，等腰直角三角形的性质，熟练掌握矩形的判断，正方形的判断，等腰直角三角形的性质是解题的关键．
7．(1)①②③或①③④（写出一种情况即可）
(2)见解析
【分析】（1）根据两三角形全等的判定条件，选择合适的条件即可；
（2）根据（1）中所选的条件，进行证明即可．
【详解】（1）解：根据题意，可以选择的条件为：①②③；
或者选择的条件为：①③④；
（2）证明：当选择的条件为①②③时，
，
，
即，
在和中，
，
；
当选择的条件为①③④时，
，
，
即，
在和中，
，
．
【点睛】本题考查了全等三角形的判定，熟知全等三角形的判定条件是解题的关键．
8．作图：见解析；；；；被平行四边形一组对边所截，截得的线段被对角线中点平分
【分析】根据线段垂直平分线的画法作图，再推理证明即可并得到结论．
【详解】解：如图，即为所求；

证明：∵四边形是平行四边形，
∴．
∴ ．
∵垂直平分，
∴．
又．
∴．
∴．
故答案为：；；；
由此得到命题：过平行四边形对角线中点的直线被平行四边形一组对边所截，截得的线段被对角线中点平分，
故答案为：被平行四边形一组对边所截，截得的线段被对角线中点平分．
【点睛】此题考查了平行四边形的性质，作线段的垂直平分线，全等三角形的判定和性质，熟练掌握平行四边形的性质及线段垂直平分线的作图方法是解题的关键．
9．(1)见解析
(2)矩形，证明见解析
【分析】（1）由平行四边形的性质得出，，，，证出，，由证明，即可得出结论；
（2）由全等三角形的性质得出，，证出，由已知得出，，即可证出四边形是平行四边形．
【详解】（1）解：证明：∵四边形是平行四边形，
∴，，，，
∴，，
∵和的平分线、分别交、于点E、F，
∴，，
∴，
在和中，
，
∴．
（2）证明：∵，
∴，，
∴，
∴，
∵点G、H分别为、的中点，
∴，，
∴四边形是平行四边形
∵，G为的中点，
∴，
∴四边形是矩形．
【点睛】本题考查了平行四边形的判定与性质、全等三角形的判定与性质、平行线的判定与性质；熟练掌握平行四边形的性质与判定，证明三角形全等是解决问题的关键．
10．(1)二
(2)见解析
【分析】（1）根据证明过程即可求解．
（2）利用全等三角形的判定及性质即可求证结论．
【详解】（1）解：则小虎同学的证明过程中，第二步出现错误，
故答案为：二．
（2）证明：∵，
，
在和中，
，
，
，
在和中，
，
，
．
【点睛】本题考查了全等三角形的判定及性质，熟练掌握其判定及性质是解题的关键．
11．(1)见解析
(2)见解析
【分析】（1）连接，交于点，证明，推出四边形为平行四边形，得到，即可得证；
（2）先证明四边形是菱形，得到，进而得到，即可得证．
【详解】（1）证明：连接，交于点，

∵四边形是平行四边形，
∴，
∵，
∴，
又，
∴，
∴，
∴四边形为平行四边形，
∴，
∴；
（2）∵四边形是平行四边形，
∴，
∴，
∵，
∴，
∴，
∴四边形是菱形，
∴，
∴，
∴平行四边形是菱形．
【点睛】本题考查平行四边形的判定和性质，菱形的判定和性质．熟练掌握相关知识点，是解题的关键．
12．（1）②①，证明见解析（或①②，证明见解析）（2）
【分析】（1）一：已知条件为②，结论为①与相切；连接，先证出，再根据平行线的性质可得，然后根据圆的切线的判定即可得证；二：已知条件为①与相切，结论为②；连接，先证出，再根据圆的切线的性质可得，然后根据平行线的性质即可得证；
（2）连接，先解直角三角形求出的长，再根据等边三角形的判定与性质可得的长，从而可得的长，然后根据圆周角定理可得，最后根据阴影部分的面积等于直角梯形的面积减去扇形的面积即可得．
【详解】解：（1）一：已知条件为②，结论为①与相切，证明如下：
如图，连接，

，
，
弦平分，
，
，
，
，
，
又是的半径，
与相切；
二：已知条件为①与相切，结论为②，证明如下：
如图，连接，

，
，
弦平分，
，
，
，
与相切，
，
；
（2）如图，连接，

，，
，，
，
又，
，
是等边三角形，
，
，
由圆周角定理得：，
则阴影部分的面积为
．
【点睛】本题考查了圆的切线的判定与性质、解直角三角形、扇形的面积、圆周角定理等知识点，熟练掌握圆的切线的判定与性质是解题关键．
13．(1)
(2)见详解
(3)见详解
【分析】（1）先证明，再证明是线段的垂直平分线，即有，即是等边三角形，问题得解；
（2）根据垂直可得，又根据，可得，即可证明；
（3）过H点作于点K，先表示出，根据是线段的垂直平分线，可得，即可得，进而可得，则有，结合，，可得，再证明，即可证明．
【详解】（1）∵，
∴，
∵，，
∴，
∴，
∵、是两个等腰直角三角形，
∴，，
∴，
∴，
∴等腰直角中，，
∴是线段的垂直平分线，
∴，
∴，即是等边三角形，
∴；
（2）在（1）中有，，
∴，
又∵，
∴，
∴；
（3）过H点作于点K，如图，

∵，，
∴，
∴，即是等腰，
∴，
∵，，，
∴，
∵是线段的垂直平分线，
∴，
在（1）中已证明，
∴，
∵，
∴，
∵，
∴，
∴，
∵，，
∴，
∵，，
∴，
∴，
∴，
∴．
【点睛】本题主要考查了等腰三角形的性质性质，相似三角形的判定与性质，等边三角形的判定与性质，作出科学的辅助线，是解答本题的关键．
14．(1)证明见解析
(2)证明见解析
【分析】（1）根据矩形的性质和折叠的性质证明，，由此即可证明得到，进而推出，再由，即可证明四边形是平行四边形；
（2）由（1）的结论可得，进一步证明，再证明，即可证明．
【详解】（1）证明：∵四边形是矩形，
∴，
由折叠的性质可得 ，
∴，
∵，，
∴，
∴，
∴，
∴，
又∵，
∴四边形是平行四边形；
（2）证明：∵四边形是平行四边形，
∴，
由折叠的性质可得，
∴，
∵，
∴，
又∵，
∴，
∴．
【点睛】本题主要考查了矩形于折叠问题，平行四边形的性质与判定，全等三角形的性质与判定等等，熟练掌握相关知识是解题的关键．
15．(1)四边形是菱形，理由见解析
(2)见解析
【分析】（1）过点A作于F，于G，先由角平分线性质得，再证明，得，证明，得，从而得出，再根据平行线性质与角平分线定义证明，得，从而得，即可得出结论；
（2）连接，过点A作于H，作于G，证明，得，证明，得，证明，得，从而得，根据平行线等分线段定理即可得出结论．
【详解】（1）解：四边形是菱形，理由如下：
过点A作于F，于G，如图1，

∵平分，，，
∴，
∵，
∴，
∴，
∵，
∴，
∴，
∴，即，
∵平分，
∴
∵
∴
∴
∴
∴，
∴四边形是菱形．
（2）证明：连接，过点A作于H，作于G，如图2，

∵平分，，，
∴，
∵，
∴，
∴，
∵，，
∴，，
∵， ，
∴，
∴，
∴，
∴，即，
∵，，
∴，
∴，
∴，
∵，，
∴，
∵，
∴．
【点睛】本题考查角平分线性质，菱形的判定，全等三解形的判定与性质，垂直定理，平行线等分线段定理，熟练掌握相关性质与判定是解题的关键．
16．(1)见解析
(2)是等腰三角形，理由见解析
(3)
【分析】（1）连接，根据圆周角定理得出，根据已知得出，根据得出，进而根据对等角相等，以及三角形内角和定理可得，即可得证；
（2）根据题意得出，则，证明，得出，等量代换得出，即可得出结论；
（3）根据，，设，则，等边对等角得出，则．
【详解】（1）证明：如图所示，连接，

∵，
∴，
∵，
∴，
∵，
∴，
∵
∴，
即，又是的直径，
∴是的切线；
（2）∵，是的直径，
∴，，
∴，
∵，，
∵，
∴，
又，
∴，
∴是等腰三角形，
（3）∵，，
设，则，
∴，
∴．
【点睛】本题考查了切线的判定，等腰三角形的性质与判定，圆周角定理，熟练掌握以上知识是解题的关键．
17．（1）见解析；（2）见解析；（3）是直角三角形，证明见解析．
【分析】（1）根据中位线定理即可求出，利用等腰三角形的性质即可证明；
（2）根据中位线定理即可求出和，通过第（1）问的结果进行等量代换即可证明；
（3）根据中位线定理推出和从而求出，证明是等边三角形，利用中点求出，从而求出度数，即可求证的形状.
【详解】证明：（1）的中点，是的中点，
.
同理，.
，
.
.
（2）的中点，是的中点，
，
.
同理，.
由（1）可知，
.
（3）是直角三角形，证明如下：
如图，取的中点，连接，，
是的中点，
，.
同理，，.
，
.
.
，
，
.
，
.
又，
是等边三角形，
.
又，
.
，
.
是直角三角形.
故答案为：是直角三角形.
【点睛】本题考查了三角形的中位线定理，等腰三角形的性质，等边三角形的性质以及直角三角形的判定，解题的关键在于灵活运用中位线定理.
18．(1)证明见详解
(2)，理由见解析
【分析】（1）由折叠的性质可得，根据题意可得，再设，然后表示出、，再由锐角三角函数求出即可；
（2）由折叠的性质可知，，从而可得出，进而得到，，由（1）知，可得，在中求出的正切值即可解答．
【详解】（1）证明：由折叠的性质可得，
，
四边形是矩形，
，
，
，
设，则，，
，
即，
，
解得，
根据勾股定理可得，
，
即，
．
解得，
，
，
点为的中点．
（2）解：，理由如下：
连接，如图：
由折叠的性质可知，，
，，
，
，
，
由（1）知，可得，
，
设，则，，
，
，
在中，，
，
，
．
【点睛】本题考查矩形的性质，折叠的性质，勾股定理，锐角三角函数，熟练掌握以上知识是解题关键．
19．(1)的度数为
(2)矩形，理由见详解
【分析】（1）根据点是的中点，沿所在的直线折叠，可得是等腰三角形，根据三角形的外角的性质即可求解；
（2）如图所示，连接，点是上的一点，根据矩形和折叠的性质可得四边形是平行四边形，如图所示，连接，，过点作于点，可证四边形是平行四边形，再根据折叠的性质得，由此即可求证．
【详解】（1）解：∵四边形是矩形，点是的中点，
∴，
∵沿所在的直线折叠，的对应点分别为，，
∴，
∴，则是等腰三角形，
∴，
∵，即，
∴，
∴的度数为．
（2）解：如图所示，连接，点是上的一点，

∵四边形是矩形，
∴，，即，
∵沿所在的直线折叠，的对应点分别为，，
∴，，是的角平分线，
由（1）可知，，
∴，
∴，且，
∴四边形是平行四边形，则，，
如图所示，连接，，过点作于点，

∵点是的中点，，
∴点是线段的中点，则，
∴在中，
，
∴，
∴，，
∵沿所在的直线折叠，的对应点分别为，，
∴，，，
在中，
，
∴，
∴，，
∴，
∴，
∴四边形是平行四边形，
∵，
∴平行四边形是矩形．
【点睛】本题主要考查矩形的性质，矩形的判定，折叠的性质，全等三角形的判定和性质的综合，掌握矩形折叠的性质，全等三角形的判定和性质，图形结合分析是解题的关键．
20．(1)点在线段的垂直平分线上
(2)①证明见解析，②
【分析】（1）根据菱形的性质及垂直平分线的判定证明即可；
（2）①根据菱形的性质得出，再由各角之间的关系得出，由含30度角的直角三角形的性质求解即可；③连接．利用等边三角形的判定和性质得出，再由正切函数及全等三角形的判定和性质及勾股定理求解即可．
【详解】（1）解：如图，点在线段的垂直平分线上．
理由如下：连接．
∵四边形是菱形，对角线相交于点，
．
，
，
∴点在线段的垂直平分线上．

（2）①证明：如图，∵四边形是菱形，
，
，，
，
，
．
，
．
，
，
，
．
在中，，
．
．
，
；

②如图，连接．
，
∴是等边三角形．
∵，
∴，
在中，，
，
．
，，
，
．
，
，
．
在中，，
由勾股定理得，
．

【点睛】题目主要考查菱形的性质，全等三角形的判定和性质，线段垂直平分线的判定和性质及解直角三角形，理解题意，综合运用这些知识点是解题关键．
21．(1)
(2)①；②的长为14或11或8或0
【分析】（1）根据平移的性质可得四边形、四边形是平行四边形，再由已知推导出是的平分线，由等腰三角形的性质可得，过点作交于点，求出，再由，所以；
（2）①证明，则；
②过点作交于，由等积法可得，求出，分三种情况讨论：当时，；当点与点重合时，，此时，当时，，在中，，可得；当时，，过点作交于，所以，能求出，，则；当时，，当点在上时，，此时点与点重合，此时．
【详解】（1）解：当点与点重合时，，
由平移可知，，，
四边形、四边形是平行四边形，
，，
，
，
，
，
，
，
是的平分线，
，
，
如图1，过点作交于点，

，
，
，
，
；
（2）解：①，理由如下：
如图2，，，，
，
；
②如图2，过点作交于，

由①可知，
，
当时，
，
，
，
，
当点与点重合时，，此时，
当时，，在中，，
；
当时，，
，
，
过点作交于，
，
，，
，
，
，
，
；
当时，
，
，
，
，
当点在上时，，此时点与点重合，
；
综上所述：的长为14或11或8或0．
【点睛】本题考查几何变换的综合应用，熟练掌握三角形平移的性质，旋转的性质，三角形全等的判定及性质，等腰三角形的性质，分类讨论是解题的关键．
22．(1)①；②；
(2)见解析；
(3)见解析
【分析】（1）①根据，结合圆周角定理求的度数；②构造直角三角形；
（2）只要说明点到圆上、和另一点的距离相等即可；
（3）根据，构造一条线段等于，利用三角形全等来说明此线段和相等．
【详解】（1）解：①，，
，
．
②连接，过作，垂足为，

，，
是等腰直角三角形，且，
，，
是等腰直角三角形，
，
在直角三角形中，，
．
（2）证明：延长交圆于点，则，

，
，
，
，
，
，
，
为该圆的圆心．
（3）证明：过作的垂线交的延长线于点，连接，延长交圆于点，连接，，

，
，
是等腰直角三角形，
，
，，
，
是直径，
，
，
，
，
，
，
，
必有一个点的位置始终不变，点即为所求．
【点睛】本题考查了圆周角定理，还考查了勾股定理和三角形全等的知识，对于（3）构造一条线段等于是关键．