模块二 知识全整合专题4 图形的性质 第10讲 与圆有关的计算（含解析） -最新中考数学二轮专题复习训练

这是一份模块二 知识全整合专题4 图形的性质 第10讲 与圆有关的计算（含解析） -最新中考数学二轮专题复习训练，共41页。试卷主要包含了知识全整合等内容，欢迎下载使用。
专题4 图形的性质
第10讲 与圆有关的计算
一、圆内正多边形的计算
1．正三角形（等边三角形）
在⊙中△是正三角形，有关计算在中进行：；
2．正四边形（正方形）
四边形的有关计算在中进行，：
3．正六边形
六边形的有关计算在中进行，．
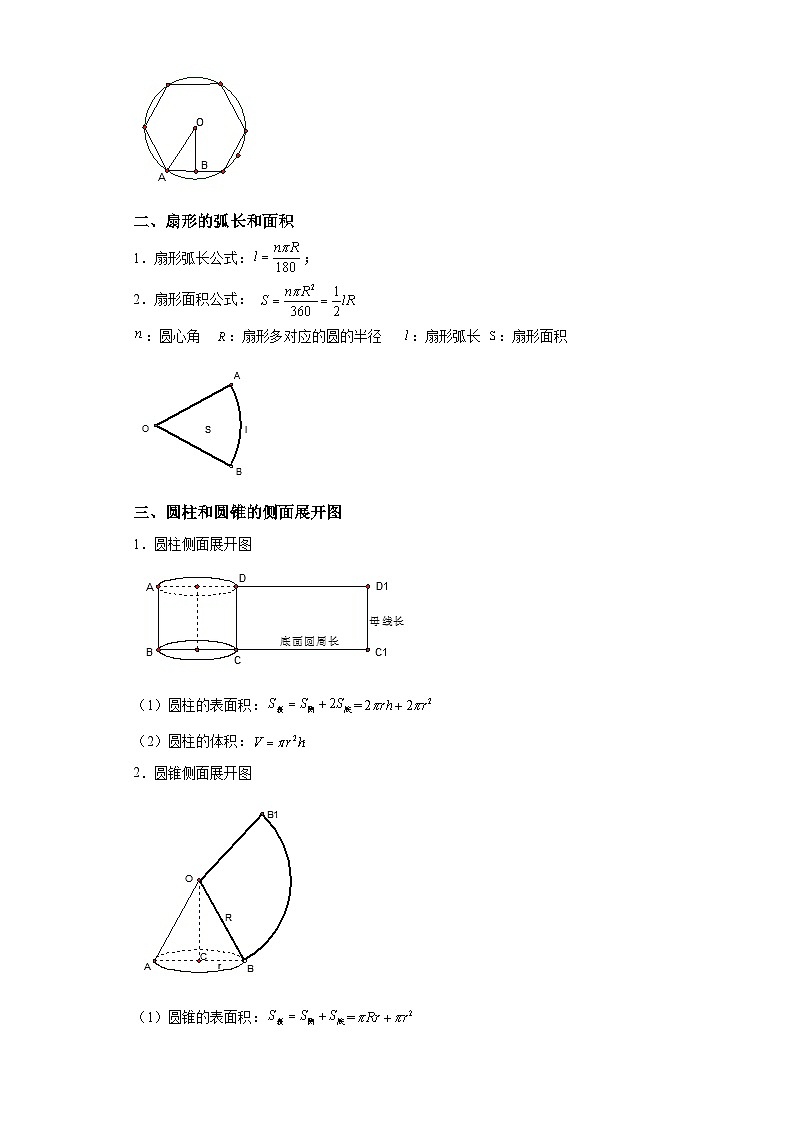
二、扇形的弧长和面积
1．扇形弧长公式：；
2．扇形面积公式：
：圆心角 ：扇形多对应的圆的半径 ：扇形弧长 ：扇形面积
三、圆柱和圆锥的侧面展开图
1．圆柱侧面展开图
（1）圆柱的表面积：=
（2）圆柱的体积：
2．圆锥侧面展开图
（1）圆锥的表面积：=
（2）圆锥的体积：
《义务教育数学课程标准》2022年版，学业质量要求：
1．能用尺规作圆的内接正方形和内接正六边形；
2．了解正多边形的概念及正多边形与圆的关系；
3．会计算圆的弧长、扇形的面积；
【例1】
（2023·湖南娄底·统考中考真题）
1．如图，正六边形的外接圆的半径为2，过圆心O的两条直线、的夹角为，则图中的阴影部分的面积为（ ）

A．B．C．D．
【变1】
2023·浙江杭州·统考中考真题）
2．如图，六边形是的内接正六边形，设正六边形的面积为，的面积为，则 ．

【例1】
（2023·辽宁沈阳·统考中考真题）
3．如图，四边形内接于，的半径为，，则的长是（ ）

A．B．C．D．
【变1】
（2023·湖北黄石·统考中考真题）
4．“神舟”十四号载人飞行任务是中国空间站建造阶段的首次载人飞行任务，也是空间站在轨建造以来情况最复杂、技术难度最高、航天员乘组工作量最大的一次载人飞行任务．如图，当“神舟”十四号运行到地球表面P点的正上方的F点处时，从点F能直接看到的地球表面最远的点记为Q点，已知，，则圆心角所对的弧长约为 km（结果保留）．

【例1】
（2023·湖北鄂州·统考中考真题）
5．如图，在中，，，，点为的中点，以为圆心，长为半径作半圆，交于点，则图中阴影部分的面积是（ ）

A．B．C．D．
【变1】
（2023·黑龙江绥化·统考中考真题）
6．如图，的半径为，为的弦，点为上的一点，将沿弦翻折，使点与圆心重合，则阴影部分的面积为 ．（结果保留与根号）

【例1】
（2023·山东聊城·统考中考真题）
7．如图，该几何体是由一个大圆锥截去上部的小圆锥后剩下的部分．若该几何体上、下两个圆的半径分别为1和2，原大圆锥高的剩余部分为，则其侧面展开图的面积为（ ）

A．B．C．D．
【变1】
（2023·内蒙古·统考中考真题）
8．如图，正六边形的边长为2，以点A为圆心，为半径画弧，得到扇形（阴影部分）．若扇形正好是一个圆锥的侧面展开图，则该圆锥的底面圆的半径是 ．

一、选择题
（2023·四川德阳·统考中考真题）
9．已知一个正多边形的边心距与边长之比为，则这个正多边形的边数是（ ）
A．4B．6C．7D．8
（2023·福建·统考中考真题）
10．我国魏晋时期数学家刘徽在《九章算术注》中提到了著名的“割圆术”，即利用圆的内接正多边形逼近圆的方法来近似估算，指出“割之弥细，所失弥少．割之又割，以至于不可割，则与圆周合体，而无所失矣”．“割圆术”孕育了微积分思想，他用这种思想得到了圆周率的近似值为3.1416．如图，的半径为1，运用“割圆术”，以圆内接正六边形面积近似估计的面积，可得的估计值为，若用圆内接正十二边形作近似估计，可得的估计值为（ ）
A．B．C．3D．
（2023·浙江台州·统考中考真题）
11．如图，的圆心O与正方形的中心重合，已知的半径和正方形的边长都为4，则圆上任意一点到正方形边上任意一点距离的最小值为（ ）．

A．B．2C．D．
（2023·安徽·统考中考真题）
12．如图，正五边形内接于，连接，则（ ）

A．B．C．D．
（2023·山东青岛·统考中考真题）
13．如图，四边形是的内接四边形，，．若的半径为5，则的长为（ ）

A．B．C．D．
（2023·内蒙古通辽·统考中考真题）
14．如图，在扇形中，，平分交于点D，点C是半径上一动点，若，则阴影部分周长的最小值为（ ）

A．B．C．D．
（2023·湖北恩施·统考中考真题）
15．如图，等圆和相交于A，B两点，经过的圆心，若，则图中阴影部分的面积为（ ）
A．B．C．D．
（2023·山东东营·统考中考真题）
16．如果圆锥侧面展开图的面积是，母线长是，则这个圆锥的底面半径是（ ）
A．3B．4C．5D．6
（2023·内蒙古赤峰·统考中考真题）
17．某班学生表演课本剧，要制作一顶圆锥形的小丑帽．如图，这个圆锥的底面圆周长为，母线长为30，为了使帽子更美观，要粘贴彩带进行装饰，其中需要粘贴一条从点A处开始，绕侧面一周又回到点A的彩带（彩带宽度忽略不计），这条彩带的最短长度是（ ）
v
A．B．C．D．
二、填空题
（2023·陕西·统考中考真题）
18．如图，正八边形的边长为2，对角线、相交于点．则线段的长为 ．

（2023·江苏盐城·统考中考真题）
19．如图，在中，，，，将绕点逆时针旋转到的位置，点的对应点首次落在斜边上，则点的运动路径的长为 .

（2023·湖南岳阳·统考中考真题）
20．如图，在中，为直径，为弦，点为的中点，以点为切点的切线与的延长线交于点．

（1）若，则的长是 （结果保留）；
（2）若，则 ．
（2023·吉林·统考中考真题）
21．如图①，A，B表示某游乐场摩天轮上的两个轿厢．图②是其示意图，点O是圆心，半径r为，点A，B是圆上的两点，圆心角，则的长为 ．（结果保留）

（2023·青海西宁·统考中考真题）
22．如图，边长为的正方形内接于，分别过点A，D作⊙O的切线，两条切线交于点P，则图中阴影部分的面积是 ．

（2023·内蒙古·统考中考真题）
23．如图，正方形的边长为2，对角线相交于点，以点为圆心，对角线的长为半径画弧，交的延长线于点，则图中阴影部分的面积为 ．

2023·湖南娄底·统考中考真题）
24．如图，在中，，，边上的高，将绕着所在的直线旋转一周得到的几何体的表面积为 ．

（2023·江苏苏州·统考中考真题）
25．如图，在中，，垂足为．以点为圆心，长为半径画弧，与分别交于点．若用扇形围成一个圆锥的侧面，记这个圆锥底面圆的半径为；用扇形围成另一个圆锥的侧面，记这个圆锥底面圆的半径为，则 ．（结果保留根号）

（2023·湖南湘西·统考中考真题）
26．如图，是等边三角形的外接圆，其半径为4．过点B作于点E，点P为线段上一动点（点P不与B，E重合），则的最小值为 ．

三、解答题
（2023·湖北襄阳·统考中考真题）
27．如图，在中，，是的中点，与相切于点，与交于点，，是的直径，弦的延长线交于点，且．

(1)求证：是的切线；
(2)若，，求的长．
（2023·湖南益阳·统考中考真题）
28．如图，线段与相切于点B，交于点M，其延长线交于点C，连接，，D为上一点且的中点为M，连接，．

(1)求的度数；
(2)四边形是否是菱形？如果是，请证明：如果不是，请说明理由；
(3)若，求的长．
（2023·山东东营·统考中考真题）
29．如图，在中，，以为直径的交于点D，，垂足为E．
(1)求证：是的切线；
(2)若，，求的长．
（2023·浙江衢州·统考中考真题）
30．如图，在中，，O为边上一点，连结，以为半径的半圆与边相切于点D，交边于点E．

(1)求证：；
(2)若，，①求半圆的半径；②求图中阴影部分的面积．
（2023·江苏南通·统考中考真题）
31．如图，等腰三角形的顶角，和底边相切于点，并与两腰，分别相交于，两点，连接，．

(1)求证：四边形是菱形；
(2)若的半径为2，求图中阴影部分的面积．
参考答案：
1．C
【分析】如图，连接，标注直线与圆的交点，由正六边形的性质可得：，，三点共线，为等边三角形，证明扇形与扇形重合，可得，从而可得答案．
【详解】解：如图，连接，标注直线与圆的交点，
由正六边形的性质可得：，，三点共线，为等边三角形，

∴，，
∴，
∴扇形与扇形重合，
∴，
∵为等边三角形，，过作于，
∴，，，
∴；
故选C
【点睛】本题考查的是正多边形与圆，扇形面积的计算，勾股定理的应用，熟记正六边形的性质是解本题的关键．
2．2
【分析】连接，首先证明出是的内接正三角形，然后证明出，得到，，进而求解即可．
【详解】如图所示，连接，

∵六边形是的内接正六边形，
∴，
∴是的内接正三角形，
∵，，
∴，
∵，
∴，
∴，
同理可得，，
又∵，
∴，
∴，
由圆和正六边形的性质可得，，
由圆和正三角形的性质可得，，
∵，
∴．
故答案为：2．
【点睛】此题考查了圆内接正多边形的性质，正六边形和正三角形的性质，全等三角形的性质和判定等知识，解题的关键是熟练掌握以上知识点．
3．C
【分析】根据圆内接四边形的性质得到，由圆周角定理得到，根据弧长的公式即可得到结论．
【详解】解：四边形内接于，，
，
，
的长．
故选：．
【点睛】本题考查的是弧长的计算，圆内接四边形的性质和圆周角定理，掌握圆内接四边形的对角互补是解题的关键．
4．
【分析】设，由是的切线，可得，由此构建方程求出r,再利用弧长公式求解．
【详解】解：设，
由题意，是的切线，
∴，
∵，
∴，
∴，
∴的长．
故答案为：．
【点睛】本题考查解直角三角形的应用，弧长公式等知识，解题的关键是学会利用参数构建方程求解．
5．C
【分析】连接，，作交于点，首先根据勾股定理求出的长度，然后利用解直角三角形求出、的长度，进而得到是等边三角形，，然后根据角直角三角形的性质求出的长度，最后根据进行计算即可．
【详解】解：如图所示，连接，，作交于点

∵在中，，，，
∴，
∵点为的中点，以为圆心，长为半径作半圆，
∴是半圆的直径，
∴，
∵，
∴，，
又∵，
∴，
∴是等边三角形，
∴，
∵，，
∴，
∴．
故选：C．
【点睛】本题考查了角直角三角形的性质，解直角三角形，等边三角形的性质和判定，扇形面积，勾股定理等知识，正确添加辅助线，熟练掌握和灵活运用相关知识是解题的关键．
6．
【分析】根据折叠的性质得出是等边三角形，则，，根据阴影部分面积即可求解．
【详解】解：如图所示，连接，设交于点

∵将沿弦翻折，使点与圆心重合，
∴，
又
∴，
∴是等边三角形，
∴，，
∴,
∴阴影部分面积
故答案为：．
7．C
【分析】根据展开面积大圆锥侧面积与小圆锥侧面积之差计算即可．
【详解】根据题意，补图如下：

∵，
∴，
∴，
∴，
∴，
∴侧面展开图的面积为，
故选C．
【点睛】本题考查了圆锥的侧面积计算，三角形相似的判定和性质，熟练掌握圆锥的侧面积计算是解题的关键．
8．
【分析】首先确定扇形的圆心角的度数，然后利用圆锥的底面圆周长是扇形的弧长计算即可．
【详解】解：∵正六边形的外角和为，
∴每一个外角的度数为，
∴正六边形的每个内角的度数为，
设这个圆锥底面圆的半径是r，
根据题意得，，
解得，
故答案为：．
【点睛】本题考查正多边形和圆及圆锥的计算，解题的关键是求得正六边形的内角的度数，并理解圆锥的母线长是扇形的半径，圆锥的底面圆周长是扇形的弧长．
9．B
【分析】如图，A为正多边形的中心，为正多边形的边，，为正多边形的半径，为正多边形的边心距，由可得，可得，而，可得为等边三角形，从而可得答案．
【详解】解：如图，A为正多边形的中心，为正多边形的边，，为正多边形的半径，为正多边形的边心距，

∴，，，
∴，
∴，即，
∴，
∴，而，
∴为等边三角形，
∴，
∴多边形的边数为：，
故选B
【点睛】本题考查的是正多边形与圆，锐角三角函数的应用，熟练的利用数形结合的方法解题是关键．
10．C
【分析】根据圆内接正多边形的性质可得，根据30度的作对的直角边是斜边的一半可得，根据三角形的面积公式即可求得正十二边形的面积，即可求解．
【详解】解：圆的内接正十二边形的面积可以看成12个全等的等腰三角形组成，故等腰三角形的顶角为，设圆的半径为1，如图为其中一个等腰三角形，过点作交于点于点，
∵，
∴，
则，
故正十二边形的面积为，
圆的面积为，
用圆内接正十二边形面积近似估计的面积可得，
故选：C．
【点睛】本题考查了圆内接正多边形的性质，30度的作对的直角边是斜边的一半，三角形的面积公式，圆的面积公式等，正确求出正十二边形的面积是解题的关键．
11．D
【分析】设正方形四个顶点分别为，连接并延长，交于点，由题意可得，的长度为圆上任意一点到正方形边上任意一点距离的最小值，求解即可．
【详解】解：设正方形四个顶点分别为，连接并延长，交于点，过点作，如下图：

则的长度为圆上任意一点到正方形边上任意一点距离的最小值，
由题意可得：，
由勾股定理可得：，
∴，
故选：D
【点睛】此题考查了圆与正多边形的性质，勾股定理，解题的关键是熟练掌握圆与正多边形的性质，确定出圆上任意一点到正方形边上任意一点距离的最小值的位置．
12．D
【分析】先计算正五边形的内角，再计算正五边形的中心角，作差即可．
【详解】∵，
∴，
故选D．
【点睛】本题考查了正五边形的外角，内角，中心角的计算，熟练掌握计算公式是解题的关键．
13．C
【分析】连接，根据圆内接四边形的性质得出，再根据三角形的内角和求出，进而得出，最后根据弧长公式即可求解．
【详解】解：连接，
∵四边形是的内接四边形，，
∴，
∵，
∴，
∴，
∴，
故选：C．

【点睛】本题主要考查了圆的内接四边形，圆周角定理，三角形的内角和，弧长公式，解题的关键是掌握圆的内接四边形对角互补，同弧所对的圆周角是圆心角的一半，三角形的内角和为，弧长．
14．A
【分析】由于是定值，只需求解的最小值即可，作点D关于对称点，连接、、，则最小值为的长度，即阴影部分周长的最小最小值为．利用角平分线的定义可求得，进而利用勾股定理和弧长公式求得和即可．
【详解】解：如图，作点D关于对称点，连接、、，

则，，，
∴，当A、C、共线时取等号，此时，最小，即阴影部分周长的最小，最小值为．
∵平分，，
∴，
∴，
在中，，
∴，
又，
∴阴影部分周长的最小值为，
故选：A．
【点睛】本题考查弧长公式、勾股定理、角平分线的定义、轴对称性质，能利用轴对称性质求解最短路径问题是解答的关键．
15．D
【分析】先证明，再把阴影部分面积转换为扇形面积，最后代入扇形面积公式即可．
【详解】如图，连接，，
∵等圆和相交于A，B两点
∴,
∵和是等圆
∴
∴是等边三角形
∴
∵,,
∴
∴．
故选：D．
【点睛】本题考查了相交弦定理，全等的判定及性质，扇形的面积公式，转化思想是解题的关键．
16．A
【分析】根据圆锥侧面积公式，进行计算即可求解．
【详解】解：设这个圆锥的底面半径是，依题意，
∴
故选：A．
【点睛】本题考查了求圆锥底面半径，熟练掌握圆锥侧面积公式是解题的关键．
17．B
【分析】根据圆锥的底面圆周长求得半径为，根据母线长求得展开后的扇形的圆心角为，进而即可求解．
【详解】解：∵这个圆锥的底面圆周长为，
∴
解得：
∵
解得：
∴侧面展开图的圆心角为
如图所示，即为所求，过点作，
∵，，则
∵，则
∴，，

故选：B．
【点睛】本题考查了圆锥侧面展开图的圆心角的度数，勾股定理解直角三角形，求得侧面展开图的圆心角为解题的关键．
18．
【分析】根据正八边形的性质得出四边形是矩形，、是等腰直角三角形，，再根据矩形的性质以及直角三角形的边角关系求出，，即可．
【详解】解：如图，过点作于，由题意可知，四边形是矩形，、是等腰直角三角形，，

在中，，，
，
同理，
，
故答案为：．
【点睛】本题考查正多边形和圆，掌握正八边形的性质以及直角三角形的边角关系是正确解答的前提．
19．
【分析】首先证明是等边三角形，再根据弧长公式计算即可．
【详解】解：在中，∵，，，
∴，
由旋转的性质得，，
，
∴是等边三角形，
∴，
∴点的运动路径的长为．
故答案为：．
【点睛】本题考查了旋转变换，含直角三角形的性质，等边三角形的判定和性质，弧长公式等知识，解题的关键是证明是等边三角形．
20．
【分析】（1）连接，根据点为的中点，根据已知条件得出，然后根据弧长公式即可求解；
（2）连接，根据垂径定理的推论得出，是的切线，则,得出，根据平行线分线段成比例得出，设，则，勾股定理求得,J进而即可求解．
【详解】解：（1）如图，连接，

∵点为的中点，
∴，
又∵，
∴，
∴，
∵，
∴，
∴，
故答案为：．
（2）解：如图，连接，

∵点为的中点，
∴，
∴，
∵是的切线，
∴,
∴
∴，
∵，
∴，
设，则，，
∴，，
∴．
故答案为：．
【点睛】本题考查了垂径定理，圆周角定理，切线的性质，弧长公式，平行线分线段成比例定理等知识，综合性较强，熟练掌握和灵活运用相关知识是解题的关键．
21．
【分析】利用弧长公式直接计算即可．
【详解】∵半径，圆心角，
∴，
故答案为：．
【点睛】本题考查了弧长计算，熟练掌握弧长公式，并规范计算是解题的关键．
22．
【分析】连接，，证明四边形是正方形，由勾股定理求得，根据阴影部分面积求解即可．
【详解】解：如图所示，连接，，

∵、是的切线，
∴，，
∵四边形是正方形，
∴，，
∴，
∴四边形是正方形，
∵，
∴，
∴，
∴阴影部分面积
故答案为：．
【点睛】本题考查切线的性质，正方形的判定与性质，扇形的面积，勾股定理等知识，熟练掌握切线的性质、正方形的判定得出圆的半径是解题的关键．
23．
【分析】根据正方形的性质得出阴影部分的面积为扇形的面积，然后由勾股定理得出，再由扇形的面积公式求解即可．
【详解】解：正方形，
∴，，
∴，
∵正方形的边长为2，
∴
∴阴影部分的面积为扇形的面积，即，
故答案为：．
【点睛】题目主要考查正方形的性质及扇形的面积公式，理解题意，将阴影部分面积进行转化是解题关键．
24．
【分析】由圆锥的侧面展开图是扇形，可得圆锥的侧面积公式，再根据题干数据进行计算即可．
【详解】解：由题意可得：旋转后的几何体是两个共底面的圆锥，
∵边上的高，
∴底面圆的周长为：，
∵，，
∴几何体的表面积为．
故答案为：．
【点睛】本题考查的是圆锥的侧面积的计算，几何体的形成，熟记圆锥的侧面积公式是解本题的关键．
25．##
【分析】由，，，，，，，，求解，，证明，可得，再分别计算圆锥的底面半径即可．
【详解】解：∵在中，，，
∴，，
∵，，
∴，，
∴，
∵，
∴，
∴，，
解得：，，
∴；
故答案为：
【点睛】本题考查的是平行四边形的性质，勾股定理的应用，锐角三角函数的应用，扇形的弧长的计算，圆锥的底面半径的计算，熟记圆锥的侧面展开图的扇形弧长等于底面圆的周长是解本题的关键．
26．6
【分析】过点P作，连接并延长交于点F，连接，根据等边三角形的性质和圆内接三角形的性质得到，，然后利用含角直角三角形的性质得到，进而求出，然后利用代入求解即可．
【详解】如图所示，过点P作，连接并延长交于点F，连接

∵是等边三角形，
∴
∵是等边三角形的外接圆，其半径为4
∴，，
∴
∴
∵
∴
∴
∵，
∴
∴
∴的最小值为的长度
∵是等边三角形，，
∴
∴的最小值为6．
故答案为：6．
【点睛】此题考查了圆内接三角形的性质，等边三角形的性质，含角直角三角形的性质等知识，解题的关键是熟练掌握以上知识点．
27．(1)见解析
(2)
【分析】（1）连接，过点作于点，根据等腰三角形的性质得为的平分线，再根据与相切于点，是的直径得，进而根据切线的判定可得到结论；
（2）过点作于点，先证得到，进而得到，再证得到，然而在中利用三角函数可求出，进而得为等边三角形，据此得，，则，最后得到弧长公式即可得到答案．
【详解】（1）证明：连接，过点作于点，
，是的中点，
为的平分线，
与相切于点，是的直径，
为的半径，
，
又，
，
即为的半径，
是的切线；
（2）解：过点作于点，
点为的圆心，
，
在和中，
，
，
，
，
，
，
，是的中点，
，
又，
，
，
，
在和中，
，
，
，
在中，，
，
，
，
，
又，
为等边三角形，
，
，
．
【点睛】此题主要考查了切线的判定和性质，等腰三角形的性质，全等三角形的判定和性质，等边三角形的判定和性质，弧长的计算公式，熟练掌握切线的判定和性质，全等三角形的判定和性质是解答此题的关键．
28．(1)
(2)是菱形，证明见解析
(3)的长为．
【分析】（1）如图，连接，证明，而，可得，再结合等腰三角形的性质可得答案；
（2）先证明，即，而，求解，可得，证明，可得，再证明，可得，从而可得结论；
（3）如图，连接，，交于，证明为等边三角形，可得，证明，，求解，再利用弧长公式进行计算即可．
【详解】（1）解：如图，连接，

∵线段与相切于点B，
∴，而，
∴，
∵，
∴；
（2）四边形是菱形，理由如下：
∵的中点为M，，
∴，即，而，
∴，
∴，
∵的中点为M，为直径，
∴，
∴，
∵，，
∴，
∴，
∴，
∴四边形是菱形．
（3）如图，连接，，交于，

∵，，
∴为等边三角形，
∴，
∴，
∵菱形，，
∴，，
∴，
∵，
∴，
∴，
∴，
，
∴的长为．
【点睛】本题考查的是全等三角形的判定与性质，等腰三角形的判定与系数，等边三角形的判定与性质，菱形的判定与性质，弧，弦，圆心角之间的关系，圆周角定理的应用，切线的性质，弧长的计算，作出合适的辅助线是解本题的关键．
29．(1)见解析；
(2)．
【分析】（1）如图：，然后根据等边对等角可得、即，再根据可得，进而得到即可证明结论；
（2）如图：连接，有圆周角定理可得，再解直角三角形可得，进而得到，然后说明，最后根据弧长公式即可解答．
【详解】（1）证明：如图：连接

∵，
∴,
∵，
∴,
∴,
∴,
∴。
∵，
∴，
∴，
∵是的半径，
∴是的切线．
（2）解：如图：连接
∵是的直径，
∴,
在中，，，
∴，
∴，
∴，
∵，
∴，
∴，
∴．
【点睛】本题主要考查了圆的切线证明、圆周角定理、解直角三角形、等腰三角形的性质等知识点，灵活运用相关知识是解答本题的关键．
30．(1)证明过程见解析
(2)①2；②
【分析】（1）连接，由切线的性质得出，证明，再由全等三角形的判定即可得出结论；
（2）①证出，再由直角三角形的性质即可求解；
②由勾股定理求出，，由三角形面积公式和扇形的面积公式求解即可．
【详解】（1）证明：如图，连接，
∵是的切线，点D为切点，
∴，
∵，，，
∴，
∴；

（2）解：①∵，
∴，
∵，
∴，
∴，
又∵，
∴，
在中，，
∴，
∵，
∴，
∴，
∴半圆O的半径为2；
②在中，，，
∴，
∴，
∵，
∴，
∴．
【点睛】本题考查切线的性质、全等三角形的判定与性质、扇形的面积公式、锐角三角函数及勾股定理，熟练掌握切线的性质是解题的关键．
31．(1)见解析
(2)
【分析】（1）连接，根据切线的性质可得，然后利用等腰三角形的三线合一性质可得，从而可得和都是等边三角形，最后利用等边三角形的性质可得，即可解答；
（2）连接交于点，利用菱形的性质可得，，，然后在中，利用勾股定理求出的长，从而求出的长，最后根据图中阴影部分的面积扇形的面积菱形的面积，进行计算即可解答．
【详解】（1）证明：连接，

和底边相切于点，
，
，，
，
，，
和都是等边三角形，
，，
，
四边形是菱形；
（2）解：连接交于点，

四边形是菱形，
，，，
在中，，
，
，
图中阴影部分的面积扇形的面积菱形的面积
，
图中阴影部分的面积为．
【点睛】本题考查了切线的性质，扇形面积的计算，等腰三角形的性质，菱形的判定与性质，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．