



所属成套资源:2025高考数学【专题复习】考点突破和专题检测
专题16 任意角与弧度制及三角函数的概念6题型分类-备战2025年高考数学一轮专题复习全套考点突破和专题检测
展开
这是一份专题16 任意角与弧度制及三角函数的概念6题型分类-备战2025年高考数学一轮专题复习全套考点突破和专题检测,文件包含专题16任意角与弧度制及三角函数的概念6题型分类-备战2025年高考数学一轮专题复习全套考点突破和专题检测原卷版docx、专题16任意角与弧度制及三角函数的概念6题型分类-备战2025年高考数学一轮专题复习全套考点突破和专题检测解析版docx等2份试卷配套教学资源,其中试卷共56页, 欢迎下载使用。
1、角的概念
(1)任意角:①定义:角可以看成平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形;
②分类:角按旋转方向分为正角、负角和零角.
(2)所有与角α终边相同的角,连同角α在内,构成的角的集合是.
(3)象限角:使角的顶点与原点重合,角的始边与x轴的非负半轴重合,那么,角的终边在第几象限,就说这个角是第几象限角;如果角的终边在坐标轴上,就认为这个角不属于任何一个象限.
(4)象限角的集合表示方法:
2、弧度制
(1)定义:把长度等于半径长的弧所对的圆心角叫做1弧度的角,用符号rad表示,读作弧度.正角的弧度数是一个正数,负角的弧度数是一个负数,零角的弧度数是0.
(2)角度制和弧度制的互化:,,.
(3)扇形的弧长公式:,扇形的面积公式:.
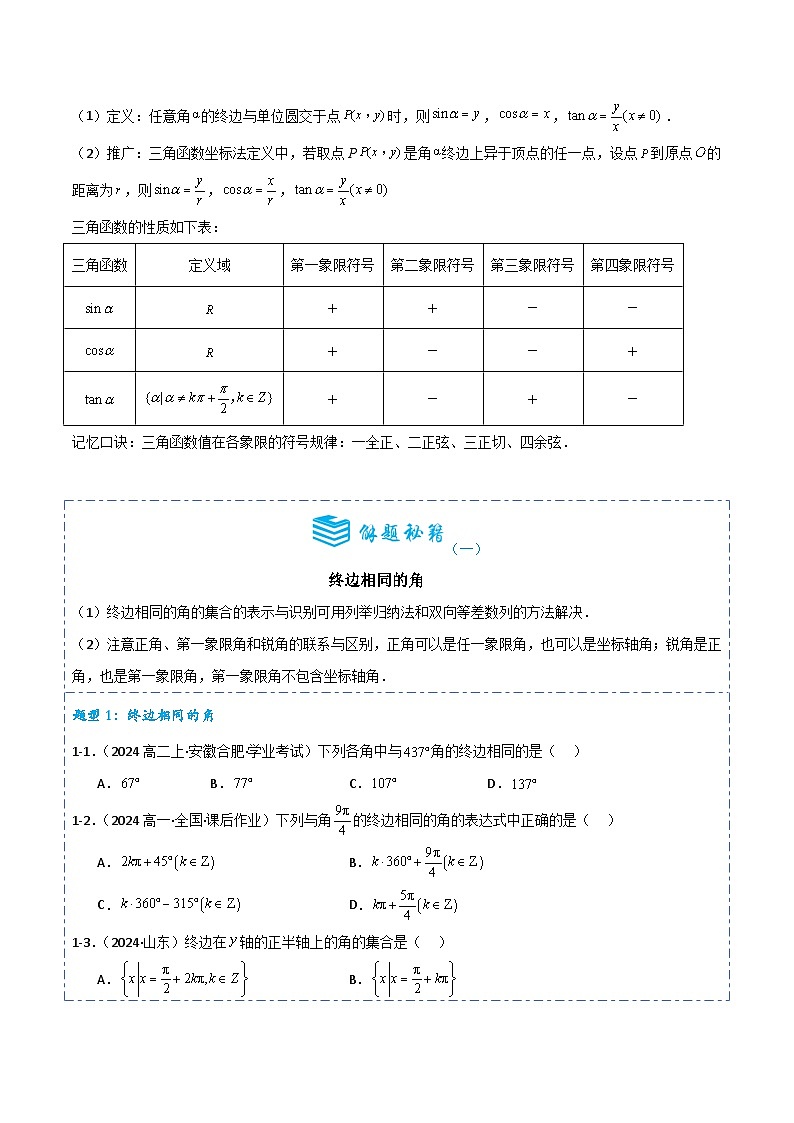
3、任意角的三角函数
(1)定义:任意角的终边与单位圆交于点时,则,,.
(2)推广:三角函数坐标法定义中,若取点P是角终边上异于顶点的任一点,设点到原点的距离为,则,,
三角函数的性质如下表:
记忆口诀:三角函数值在各象限的符号规律:一全正、二正弦、三正切、四余弦.
一、单选题
1.(2024·全国)沈括的《梦溪笔谈》是中国古代科技史上的杰作,其中收录了计算圆弧长度的“会圆术”,如图,是以O为圆心,OA为半径的圆弧,C是AB的中点,D在上,.“会圆术”给出的弧长的近似值s的计算公式:.当时,( )
A.B.C.D.
2.(2024高三上·安徽合肥·阶段练习)已知扇形的圆心角弧度为2,所对弦长为6,则该扇形的面积为( )
A.B.C.D.
3.(2024高三·全国·专题练习)在平面直角坐标系中,角的顶点为原点,以轴的非负半轴为始边,终边经过点,则下列各式的值恒大于0的有( )个.
①;②;③;④.
A.0B.1C.2D.3
4.(2024·新疆·一模)已知集合,则集合的元素个数为( )
A.3B.2C.4D.5
5.(2024高三上·浙江·阶段练习)我国魏晋时期的数学家刘徽创造性的提出了“割圆术”,刘徽认为圆的内接正边形随着边数的无限增大,圆的内接正边形的周长就无限接近圆的周长,并由此求得圆周率的近似值.如图当时,圆内接正六边形的周长为,故,即.运用“割圆术”的思想,下列估算正确的是( )
A.时,B.时,
C.时,D.时,
6.(2024高三上·河北邢台·期末)已知锐角的顶点在原点,始边在轴非负半轴,现将角的终边绕原点逆时针转后,交以原点为圆心的单位圆于点,则的值为( )
A.B.C.D.
7.(2024高三上·辽宁·阶段练习)2023年8月8日,第31届世界大学生夏季运动会(成都世界大学生运动会)完美收官.在倒计时100天时,成都大运会发布了官方体育图标——“十八墨宝”.这组“水墨熊猫”以大熊猫“奇一”为原型,将中国体育与中国书画、中国国宝的融合做到了极致.“十八般武艺”造就“十八墨宝”,花式演绎十八项体育竞技,代表了体操、游泳、羽毛球等18个成都大运会竞赛项目,深受广大人民喜爱.其中,射箭的水墨熊猫以真实的射箭运动为原型,拉满弓箭时,弓臂为圆弧形,弧中点到弦中点的距离为2cm,弦长为8cm,则弓形的面积约为(参考数据:,)( )
A.B.C.D.
8.(2024高三·全国·专题练习)集合中的角所表示的范围(阴影部分)是( )
A. B.
C. D.
9.(2024·四川绵阳·模拟预测)月牙泉,古称沙井,俗名药泉,自汉朝起即为“敦煌八景”之一,得名“月泉晓澈”,因其形酷似一弯新月而得名.如图所示,某月牙泉模型的边缘都可以看作是圆弧,两段圆弧可以看成是的外接圆和以AB为直径的圆的一部分,若,AB的长约为,则该月牙泉模型的面积约为( )
A.B.
C.D.
10.(2024高三上·重庆·阶段练习)“莱洛三角形”是机械学家莱洛研究发现的一种曲边三角形,它在很多特殊领域发挥了超常的贡献值.“莱洛三角形”是分别以正三角形的顶点为圆心,以其边长为半径作圆弧,由这三段圆弧组成的曲边三角形(如图所示).现以边长为4的正三角形作一个“莱洛三角形”,则此“莱洛三角形”的面积为( )
A.B.C.D.
11.(2024高三上·河北承德·期中)甲、乙两个圆锥的母线长相等,侧面展开图的圆心角之和为,圆锥的高分别为和,侧面积分别为和,若,则( )
A.2B.C.D.
12.(2024高三上·安徽·期中)扇子是引风用品,夏令必备之物.我国传统扇文化源远流长,是中华文化的一个组成部分.历史上最早的扇子是一种礼仪工具,后来慢慢演变为纳凉、娱乐、观赏的生活用品和工艺品.扇子的种类较多,受大众喜爱的有团扇和折扇.如图1是一把折扇,是用竹木做扇骨,用特殊纸或绫绢做扇面而制成的.完全打开后的折扇为扇形(如图2),若图2中,,分别在,上,,的长为,则该折扇的扇面的面积为( )
图1 图2
A.B.C.D.
13.(2024·河北·模拟预测)已知两圆锥的底面积分别为、,其侧面展开图中圆心角之和为,则两圆锥的母线长之和的最小值为( )
A.B.C.D.
14.(2024高三上·河南·期中)已知一个圆锥的侧面展开图是一个圆心角为的扇形,若该圆锥底面圆的半径为1,则该圆锥的体积为( )
A.B.C.D.
15.(2024高三上·福建·期中)如图是杭州2023年第19届亚运会会徽,名为“潮涌”,主体图形由扇面、钱塘江、钱江潮头、赛道、互联网符号及象征亚奥理事会的太阳图形六个元素组成,集古典美和现代美于一体,富有东方神韵和时代气息.其中扇面的圆心角为,从里到外半径以1递增,若这些扇形的弧长之和为(扇形视为连续弧长,中间没有断开),则最小扇形的半径为( )
A.6B.8C.9D.12
16.(2024高三上·安徽合肥·阶段练习)若扇形的周长等于40cm,则扇形面积的最大值是( )cm2.
A.400B.200C.100D.50
17.(2024·全国·模拟预测)甲、乙两个圆锥的底面半径相等,均为,侧面展开图的圆心角之和为,表面积之和为.则底面半径的最大值为( )
A.B.C.D.
18.(2024高一下·河北张家口·期中)如图,已知扇形的周长为,当该扇形的面积取最大值时,弦长( )
A.B.C.D.
19.(2024高三上·广东·学业考试)已知角的顶点为坐标原点,始边为x轴的正半轴,终边过点(3,4),则角的正切值为( )
A.B.C.D.
20.(2024高三上·重庆渝北·阶段练习)已知角终边上有一点,则是( )
A.第一象限角B.第二象限角
C.第三象限角D.第四象限角
21.(2024高三·全国·专题练习)已知角的始边与x轴的非负半轴重合,终边过点,则的值为( )
A.B.C.D.
22.(2024·辽宁·一模)已知角的终边上一点的坐标为,则的最小正值为( )
A.B.C.D.
23.(2024高三·全国·专题练习)若角α是第二象限角,则角2α的终边不可能在( )
A.第一、二象限B.第二、三象限
C.第三、四象限D.第一、四象限
24.(2024高三上·湖北黄冈·期中)若角满足=(k∈Z),则的终边一定在( )
A.第一象限或第二象限或第三象限
B.第一象限或第二象限或第四象限
C.第一象限或第二象限或x轴非正半轴上
D.第一象限或第二象限或y轴非正半轴上
25.(2024高一下·河南焦作·期中)已知角的终边与的终边重合,则的终边不可能在( )
A.第一象限B.第二象限C.第三象限D.第四象限
26.(2024高一下·陕西榆林·阶段练习)若角是第一象限角,则是( )
A.第一象限角B.第二象限角
C.第一或第三象限角D.第二或第四象限角
27.(2024高一下·陕西渭南·阶段练习)已知点是第二象限的点,则的终边位于( )
A.第一象限B.第二象限C.第三象限D.第四象限
28.(2024高三上·河南许昌·期末)在平面直角坐标系中,点位于第( )象限
A.一B.二C.三D.四
29.(2024·河南·模拟预测)已知是第二象限角,则点(,)所在的象限是( )
A.第一象限B.第二象限C.第三象限D.第四象限
30.(2024·河南·模拟预测)已知是第二象限角,则点所在的象限是( )
A.第一象限B.第二象限C.第三象限D.第四象限
31.(2024高三下·江西·阶段练习)已知点是角终边上一点,若,则( )
A.B.C.D.
32.(2024高一·全国·课后作业)设,角的终边与圆的交点为,那么( )
A.B.C.D.
33.(2024·北京丰台·三模)已知点的坐标为,将绕坐标原点逆时针旋转至,则点的纵坐标为( )
A.B.C.D.1
34.(2024高三·全国·对口高考)如果点P在角的终边上,且,则点P的坐标是( )
A.B.C.D.
35.(2024高三下·湖南邵阳·学业考试)已知 是角终边上的一点,则( )
A.B.C.D.
二、多选题
36.(2024高二下·广东·期末)在平面直角坐标系中,点绕点O逆时针旋转后到达点,若,则可以取( )
A.B.C.D.
37.(2024高三上·重庆沙坪坝·阶段练习)已知角的终边落在第二象限,则下列不等式一定成立的是( )
A.B.C.D.
三、填空题
38.(2024高三·全国·对口高考)①若角与角的终边相同,则与的数量关系为 ;②若角与角的终边关于x轴对称,则与的数量关系为 ;③若角与角的终边关于y轴对称,则与的数量关系为 ;④若角与角的终边在一条直线上,则与的数量关系为 ;⑤如果是第一象限的角,那么是第 象限的角.
39.(2024·山东)某中学开展劳动实习,学生加工制作零件,零件的截面如图所示.O为圆孔及轮廓圆弧AB所在圆的圆心,A是圆弧AB与直线AG的切点,B是圆弧AB与直线BC的切点,四边形DEFG为矩形,BC⊥DG,垂足为C,tan∠ODC=,,EF=12 cm,DE=2 cm,A到直线DE和EF的距离均为7 cm,圆孔半径为1 cm,则图中阴影部分的面积为 cm2.
40.(2024·全国·模拟预测)已知直线与圆交于,两点,则劣弧所对应的扇形的面积为 .
41.(2024高三·全国·专题练习)已知扇形的周长为40,则当扇形的面积最大时,它的半径和圆心角分别为 .
42.(2024·北京)若点关于轴对称点为,写出的一个取值为 .
43.(2024高三上·北京顺义·期中)已知命题:若为第一象限角,且,则.能说明命题为假命题的一组的值可以是 , .
44.(2024高三上·重庆·阶段练习)若扇形的半径为2,面积为,则扇形的周长为 .
45.(2024高一·全国·课后作业)如图所示,在平面直角坐标系中,动点P,Q从点出发在单位圆上运动,点P按逆时针方向每秒钟转弧度,点Q按顺时针方向每秒钟转弧度,则P,Q两点在第2019次相遇时,点P的坐标为 .
四、解答题
46.(2024高三·全国·专题练习)已知一扇形的圆心角为α,半径为R,弧长为l.
(1)若α=60°,R=10 cm,求扇形的弧长l;
(2)已知扇形的周长为10 cm,面积是4 cm2,求扇形的圆心角;
(3)若扇形周长为20 cm,当扇形的圆心角α为多少弧度时,这个扇形的面积最大?
47.(2024高一·全国·课后作业)如图,点是圆上的点.
(1)若,,求劣弧的长;
(2)已知扇形的周长为,求这个扇形的面积取得最大值时圆心角的大小.
48.(2024高一下·江西赣州·阶段练习)已知一扇形的圆心角为,半径为,弧长为.
(1)已知扇形的周长为,面积是,求扇形的圆心角;
(2)若扇形周长为,当扇形的圆心角为多少弧度时,这个扇形的面积最大?并求此扇形的最大面积.
49.(2024高三·全国·专题练习)已知角终边经过点,且.求的值.
三角函数
定义域
第一象限符号
第二象限符号
第三象限符号
第四象限符号
+
+
-
-
+
-
-
+
+
-
+
-
(一)
终边相同的角
(1)终边相同的角的集合的表示与识别可用列举归纳法和双向等差数列的方法解决.
(2)注意正角、第一象限角和锐角的联系与区别,正角可以是任一象限角,也可以是坐标轴角;锐角是正角,也是第一象限角,第一象限角不包含坐标轴角.
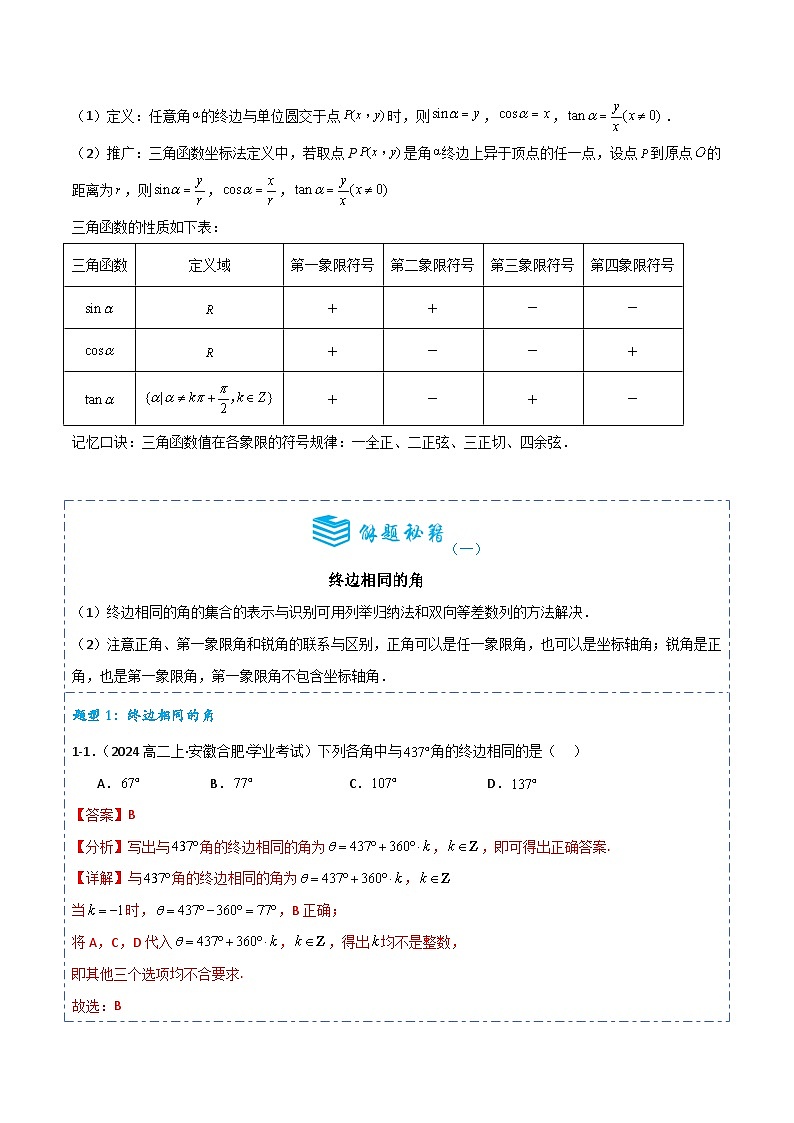
题型1:终边相同的角
1-1.(2024高二上·安徽合肥·学业考试)下列各角中与角的终边相同的是( )
A.B.C.D.
1-2.(2024高一·全国·课后作业)下列与角的终边相同的角的表达式中正确的是( )
A.B.
C.D.
1-3.(2024·山东)终边在轴的正半轴上的角的集合是( )
A.B.
C.D.
1-4.(2024高一·全国·专题练习)若角的终边与角的终边相同,则在内与角的终边相同的角是 .
(二)
角的象限问题
图象法
在平面直角坐标系中,作出已知角并根据象限角的定义直接判断已知角是第几象限角
转化法
先将已知角化为k·360°+α(0°≤α
相关试卷
这是一份专题26 数列的概念6题型分类-备战2025年高考数学一轮专题复习全套考点突破和专题检测,文件包含专题26数列的概念6题型分类-备战2025年高考数学一轮专题复习全套考点突破和专题检测原卷版docx、专题26数列的概念6题型分类-备战2025年高考数学一轮专题复习全套考点突破和专题检测解析版docx等2份试卷配套教学资源,其中试卷共60页, 欢迎下载使用。
这是一份专题18 三角恒等变换7题型分类-备战2025年高考数学一轮专题复习全套考点突破和专题检测,文件包含专题18三角恒等变换7题型分类-备战2025年高考数学一轮专题复习全套考点突破和专题检测原卷版docx、专题18三角恒等变换7题型分类-备战2025年高考数学一轮专题复习全套考点突破和专题检测解析版docx等2份试卷配套教学资源,其中试卷共79页, 欢迎下载使用。
这是一份专题08 函数的图象6题型分类-备战2025年高考数学一轮专题复习全套考点突破和专题检测,文件包含专题08函数的图象6题型分类-备战2025年高考数学一轮专题复习全套考点突破和专题检测原卷版docx、专题08函数的图象6题型分类-备战2025年高考数学一轮专题复习全套考点突破和专题检测解析版docx等2份试卷配套教学资源,其中试卷共122页, 欢迎下载使用。









