

河北省沧州市东光县五校联考2024-2025学年九年级上学期11月期中数学试题(无答案)
展开
这是一份河北省沧州市东光县五校联考2024-2025学年九年级上学期11月期中数学试题(无答案),共7页。
本试卷共8页.总分120分,考试时间120分钟.
注意事项:1.仔细审题,工整作答,保持卷面整洁.
2.考生完成试卷后,务必从头到尾认真检查一遍.
一、选择题(本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.一元二次方程用直接开平方法可转化为两个一元一次方程,其中一个一元一次方程,则另一个一元一次方程( )
A.B.C.D.
2.二次函数的图象与y轴的交点坐标为( )
A.(0,2)B.(0,1)C.(0,3)D.(0,-1)
3.把分别标着7,4,4,5,4,1,7,5这些数的八张卡片打乱后反扣在桌子上,从中任意摸一张,摸到可能性最大的数是( )
A.1B.4C.5D.7
4.如图,△DEF是由△ABC绕着点O顺时针旋转得到的,以下说法不一定正确的是( )
A.∠COF=∠BOEB.∠BAC=∠EDFC.OC=OFD.BC=DF
5.已知关于x的一元二次方程有两个不相等的实数根,则k的取值范围为( )
A.k>0且k≠1B.k≥0且k≠1C.k≥0D.k>0
6.将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上,点A,B的读数分别为85°,31°,则∠ACB的度数是( )
A.54°B.27°C.56°D.28°
7.如图,扇形OAB是圆锥的侧面展开图,点O,A,B在格点上.若小正方形方格的边长为2cm,则这个圆锥的底面半径是( )
A.B.C.D.
8.嘉淇去商场购物,购买后,商家有一个抽奖答谢活动,共有m张奖券,其中含奖项的奖券有n张,每名已购物的顾客只能抽去取一次,嘉淇抽之前有8名顾客已抽过奖券,中奖的有3人,则嘉淇中奖的概率为( )
A.B.C.D.
9.抛物线与抛物线关于原点对称,则的值为( )
A.-6B.8C.6D.9
10.如图,在△ABC中,∠ACB=90°,BC=1,,将△ABC绕着点A逆时针旋转90°得到△ADE,则图中阴影部分的面积是( )
A.B.C.D.
11.已知二次函数(a,b,c为常数,a≠0)的图象如图所示,有下列四个结论,其中正确的是( )
①一元二次方程的根为,;
②若点,在该抛物线上,则;
③对于任意实数m,都有;
④若(p为常数,p>0)的根为整数,则p的值只有两个
A.①②B.①③C.③④D.①③④
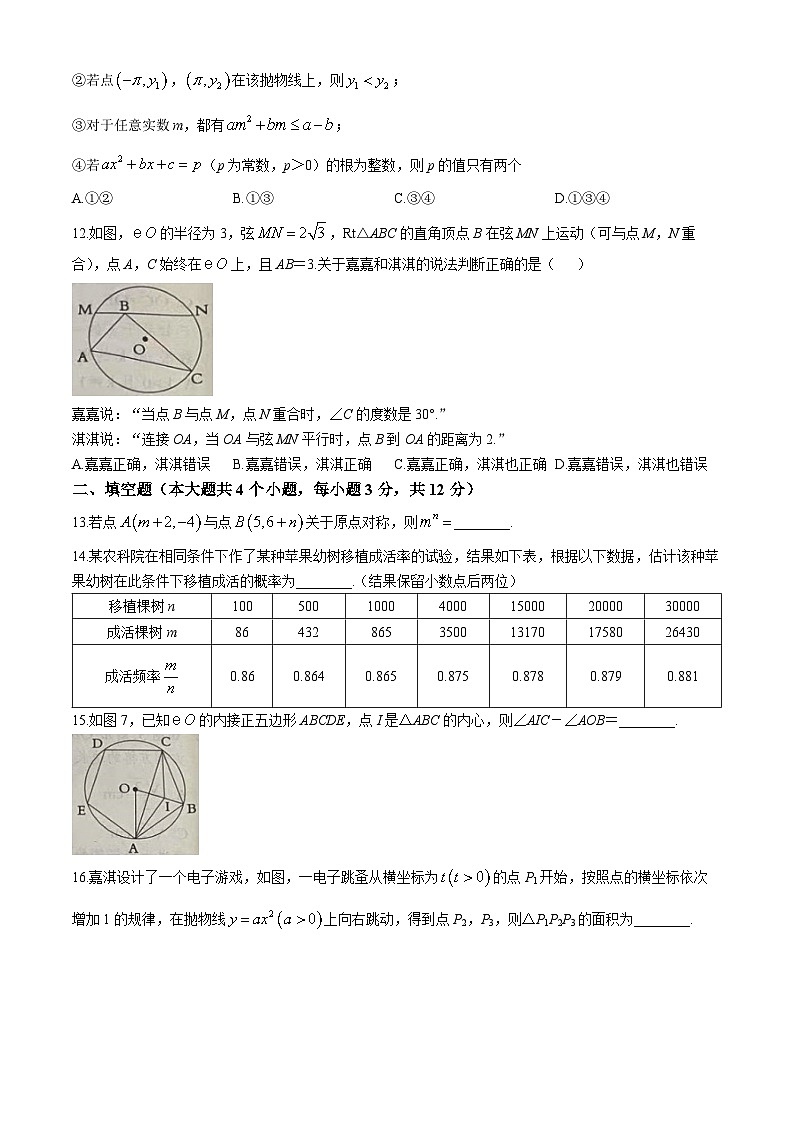
12.如图,的半径为3,弦,Rt△ABC的直角顶点B在弦MN上运动(可与点M,N重合),点A,C始终在上,且AB=3.关于嘉嘉和淇淇的说法判断正确的是( )
嘉嘉说:“当点B与点M,点N重合时,∠C的度数是30°.”
淇淇说:“连接OA,当OA与弦MN平行时,点B到OA的距离为2.”
A.嘉嘉正确,淇淇错误B.嘉嘉错误,淇淇正确C.嘉嘉正确,淇淇也正确D.嘉嘉错误,淇淇也错误
二、填空题(本大题共4个小题,每小题3分,共12分)
13.若点与点关于原点对称,则________.
14.某农科院在相同条件下作了某种苹果幼树移植成活率的试验,结果如下表,根据以下数据,估计该种苹果幼树在此条件下移植成活的概率为________.(结果保留小数点后两位)
15.如图7,已知的内接正五边形ABCDE,点I是△ABC的内心,则∠AIC-∠AOB=________.
16.嘉淇设计了一个电子游戏,如图,一电子跳蚤从横坐标为的点P1开始,按照点的横坐标依次增加1的规律,在抛物线上向右跳动,得到点P2,P3,则△P1P2P3的面积为________.
三、解答题(本大题共8个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
17. (本小题满分8分)如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别为,,.
(1)作△ABC关于原点O的中心对称图形△DEF(点A,B,C的对应点分别为点D,E,F);
(2)将△ABC绕着原点O逆时针旋转90°得到△PQR(点A,B,C的对应点分别为点P,Q,R),请画出△PQR,并写出点A的对应点点P的坐标.
18.(本小题满分8分)一个小正方体的展开图如图所示,已知正方体相对两个面上的数相同,且不相对两个面上的数值不相等.
(1)求出符合要求的x的值;
(2)已知一抛物线顶点的横、纵坐标正好是小正方体相邻两个面的数值,且该抛物线经过的另外一点横、纵坐标正好是小正方体的其他相邻的两个面的数值,判断是否在该抛物线上?
19.(本小题满分8分)如图1,有一个质地均匀且四个面上分别标有数字“1”“2”“3”“4”的正四面体骰子,小明与小红按照以下规则进行游戏活动:两人轮流掷这枚骰子,骰子着地的数字是几,就将棋子前进几格,开始棋子在数字“1”的那一格.例如:小明先掷骰子,所掷骰子着地一面所示数字为3,则棋子前进到数字4那一格.
图1 图2
(1)小明掷出骰子,数字“6”着地是________;
A.不可能事件B.必然事件C.随机事件
(2)小明先掷骰子,小红再掷。补全图2中的树状图,并分析第一轮结束后,棋子前进到数字“6”那一格的概率.
20.(本小题满分8分)如图,在△ABC中,CA=CB,以BC为直径的⊙O分别与AB,AC相交于点D,E,过点D作,垂足为F.
(1)求证:DF是⊙O的切线;
(2)分别延长CB,FD相交于点G,∠A=60°,⊙O的半径为6,求阴影部分的周长.
21.(本小题满分9分)素材1:下图是拟建中的一个温室平面设计图纸,图纸上1个单位长度代表实际距离1米,温室ABCD(BC>CD)是一个矩形,其周长为120,准备在它的四周铺设道路,左右两条纵向道路的宽度都为1,上边横向道路的宽度为1,下边横向道路的宽度为3,中间部分(阴影部分)种植草莓,种植面积为720.
素材2:道路的路面造价是70元/平方米;经市场调查,草莓培育一年可产果,已知每平方米的草莓销售平均利润为100元;其余费用为3万元.
任务1:(1)实际中温室的长不能大于35米,通过计算说明拟建的温室是否达标;
任务2:(2)求经过1年后,温室年净利润为多少?(净利润=草莓销售的总利润-路面造价费用-其余费用)
22.(本小题满分9分)某公司生产一种建筑材料,生产费用y(万元)由材料费用、人工费用和制造费用三部分组成.已知该公司每年的材料费用(万元)与生产吨数x(吨)成正比,制造费用(万元)与生产吨数x(吨)的平方成正比,人工费用为固定费用1000万元,试行中得到了下表中的数据.
(1)求y与x的函数解析式;
(2)已知卖出x吨该建筑材料的单价为P万元/吨,其中(a为常数).设出售x吨时的利润为w万元
①求w与x的函数解析式;
②如果生产出来的产品全部卖掉,并且当生产吨数是150吨时,所获利润最大,求此时P的值.
23.(本小题满分10分)如图1,在平行四边形ABCD中,∠D=135°,,过点C作边AB的垂线,交直线AB于点H,点O在直线AB上,半圆O以O为圆心,直径为EF,且EF=BH.将半圆O连同直径EF一起沿直线AB向左平移.
图1 图2 备用图
(1)半圆O的半径为________cm;
(2)当半圆O与CH相切,切点为H时,如图2所示,设点M为半圆O上一点,点N为线段BC上一点,求MN的最大值和最小值分别是多少;
(3)当半圆O平移到与CH相切时,半圆O连同直径EF一起绕着点H继续以每秒5°的速度逆时针旋转,旋转时间为9秒时,判断半圆O与直线BC的位置关系,并给出证明.
24.(本小题满分12分)如图,抛物线与抛物线交于点,且分别与y轴交于点D,E,过点B作x轴的平行线,分别交两条抛物线于点A,C.
(1)直接写出a,m的值;
(2)嘉嘉说:可由向左平移3个单位长度,再向上平移3个单位长度得到.
琪琪说:无论x为何值,y2恒小于0.
请选择其中一人的说法进行说理;
(3)推断以A,D,C,E为顶点的四边形是哪种特殊的四边形,并直接写出抛物线与在该四边形内部(包括边界)的部分的整点(横、纵坐标都为整数)个数;
(4)作直线AD,将直线AD向下平移n(n>0)个单位长度后得到直线l,直线l与抛物线,相交,直接写出直线l与抛物线,有三个交点时n的值.题号
一
二
三
17
18
19
20
21
22
23
24
得分
移植棵树n
100
500
1000
4000
15000
20000
30000
成活棵树m
86
432
865
3500
13170
17580
26430
成活频率
0.86
0.864
0.865
0.875
0.878
0.879
0.881
生产吨数(吨)
50
70
生产费用(万元)
1500
1840
相关试卷
这是一份河北省沧州市东光县五校联考2024-2025学年七年级上学期10月月考数学试卷(含答案),共12页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
这是一份河北省沧州市东光县东光县五校联考2024-2025学年七年级上学期10月月考数学试题(无答案),共4页。试卷主要包含了选择题.,填空题,解答题等内容,欢迎下载使用。
这是一份河北省沧州市东光县东光县五校联考2024-—2025学年八年级上学期10月月考数学试题(无答案),共6页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。









