

2025年高考数学一轮复习讲义(知识梳理+真题自测+考点突破+分层检测)专题01集合(新高考专用)(原卷版+解析)
展开【知识梳理】2
【真题自测】3
【考点突破】8
【考点1】集合的基本概念8
【考点2】集合间的基本关系11
【考点3】集合的运算14
【分层检测】18
【基础篇】18
【能力篇】25
【培优篇】28
考试要求:
1.了解集合的含义,理解元素与集合的属于关系,能在自然语言、图形语言的基础上,用符号语言刻画集合.
2.理解集合间包含与相等的含义,能识别给定集合的子集.
3.在具体情境中,了解全集与空集的含义.
4.理解两个集合的并集、交集与补集的含义,会求两个简单集合的并集、交集与补集.
5.能使用Venn图表达集合间的基本关系与基本运算.
知识梳理
1.元素与集合
(1)集合中元素的三个特性:确定性、互异性、无序性.
(2)元素与集合的关系是属于或不属于,表示符号分别为∈和∉.
(3)集合的三种表示方法:列举法、描述法、图示法.
(4)常用数集及记法
2.集合间的基本关系
(1)子集:一般地,对于两个集合A,B,如果集合A中任意一个元素都是集合B中的元素,就称集合A为集合B的子集.记作A⊆B(或B⊇A).
(2)真子集:如果集合A⊆B,但存在元素x∈B,且x∉A,就称集合A是集合B的真子集,记作AB(或BA).
(3)相等:若A⊆B,且B⊆A,则A=B.
(4)空集的性质:∅是任何集合的子集,是任何非空集合的真子集.
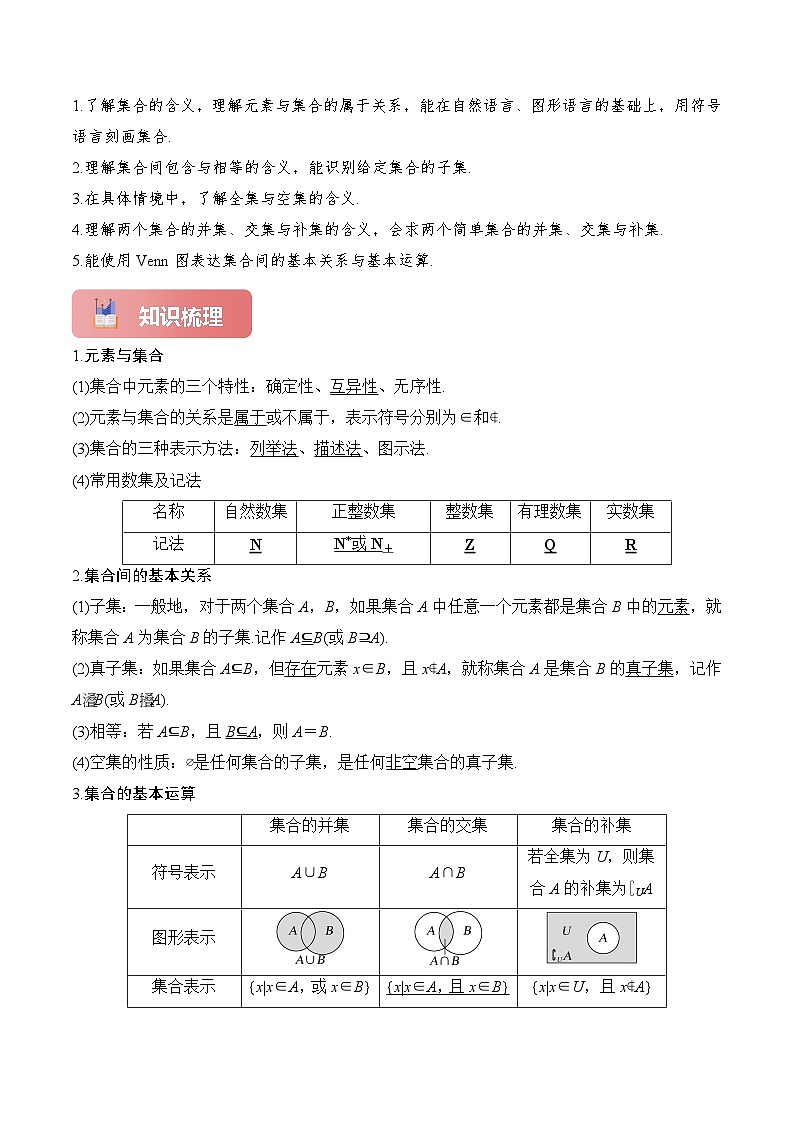
3.集合的基本运算
4.集合的运算性质
(1)A∩A=A,A∩∅=∅,A∩B=B∩A.
(2)A∪A=A,A∪∅=A,A∪B=B∪A.
(3)A∩(∁UA)=∅,A∪(∁UA)=U,∁U(∁UA)=A.
1.若有限集A中有n个元素,则A的子集有2n个,真子集有2n-1个,非空子集有2n-1个,非空真子集有2n-2个.
2.注意空集:空集是任何集合的子集,是非空集合的真子集.
3.A⊆B⇔A∩B=A⇔A∪B=B⇔∁UA⊇∁UB.
4.∁U(A∩B)=(∁UA)∪(∁UB),∁U(A∪B)=(∁UA)∩(∁UB).
真题自测
一、单选题
1.(2023·全国·高考真题)设全集,集合,( )
A.B.
C.D.
2.(2023·全国·高考真题)已知等差数列的公差为,集合,若,则( )
A.-1B.C.0D.
3.(2023·全国·高考真题)设集合,集合,,则( )
A.B.
C.D.
4.(2023·全国·高考真题)已知集合,,则( )
A.B.C.D.
5.(2023·全国·高考真题)设集合,,若,则( ).
A.2B.1C.D.
6.(2022·全国·高考真题)已知集合,则( )
A.B.C.D.
7.(2022·全国·高考真题)设全集,集合,则( )
A.B.C.D.
8.(2022·全国·高考真题)设全集,集合M满足,则( )
A.B.C.D.
9.(2022·全国·高考真题)若集合,则( )
A.B.C.D.
10.(2021·全国·高考真题)设集合,则( )
A.B.C.D.
11.(2021·全国·高考真题)已知集合,,则( )
A.B.C.D.
12.(2021·全国·高考真题)设集合,则( )
A.B.
C.D.
考点突破
【考点1】集合的基本概念
一、单选题
1.(2023·江苏·一模)设,,则( )
A.B.C.D.
2.(2023·北京海淀·模拟预测)设集合,若,则实数m=( )
A.0B.C.0或D.0或1
二、多选题
3.(22-23高一下·湖南邵阳·开学考试)若对任意,,则称为“影子关系”集合,下列集合为“影子关系”集合的是( )
A.B.C.D.
4.(2021·全国·模拟预测)设集合,若,,,则运算可能是( )
A.加法B.减法C.乘法D.除法
三、填空题
5.(2024·辽宁葫芦岛·一模)已知集合,.若,则实数的取值集合为 .
6.(2023·湖北·二模)已知X为包含v个元素的集合(,).设A为由X的一些三元子集(含有三个元素的子集)组成的集合,使得X中的任意两个不同的元素,都恰好同时包含在唯一的一个三元子集中,则称组成一个v阶的Steiner三元系.若为一个7阶的Steiner三元系,则集合A中元素的个数为 .
反思提升:
1.研究集合问题时,首先要明确构成集合的元素是什么,即弄清该集合是数集、点集,还是其他集合;然后再看集合的构成元素满足的限制条件是什么,从而准确把握集合的含义.
2.利用集合元素的限制条件求参数的值或确定集合中元素的个数时,要注意检验集合中的元素是否满足互异性.
【考点2】集合间的基本关系
一、单选题
1.(2024·全国·模拟预测)若集合,,则集合的真子集的个数为( )
A.0B.1C.2D.3
2.(2024·全国·模拟预测)已知集合,.若,则的取值范围是( )
A.B.
C.D.
二、多选题
3.(23-24高一上·陕西西安·期中)下列说法正确的是( )
A.
B.集合
C.函数的值域为
D.在定义域内单调递增
4.(2024·甘肃定西·一模)设集合,则( )
A.
B.的元素个数为16
C.
D.的子集个数为64
三、填空题
5.(2024·全国·模拟预测)已知全集,集合,.若,则的最大值为 .
6.(2021·山东淄博·模拟预测)已知数列为等差数列,数列为等比数列.若集合,集合,集合(,),且,则 .
反思提升:
1.若B⊆A,应分B=∅和B≠∅两种情况讨论.
2.已知两个集合间的关系求参数时,关键是将两个集合间的关系转化为元素或区间端点间的关系,进而求得参数范围.注意合理利用数轴、Venn图帮助分析及对参数进行讨论.求得参数后,一定要把端点值代入进行验证,否则易增解或漏解.
【考点3】集合的运算
一、单选题
1.(2024·全国·模拟预测)已知集合,,则( )
A.B.C.D.
2.(2024·全国·模拟预测)已知集合,,则( )
A.B.C.D.
二、多选题
3.(2022·重庆·模拟预测)已知全集,集合,则关于的表达方式正确的有( )
A.B.
C.D.
4.(23-24高三上·海南省直辖县级单位·阶段练习)图中阴影部分所表示的集合是( )
A.B.C.D.
三、填空题
5.(2020·江苏南通·模拟预测)某单位周一、周二、周三开车上班的职工人数分别是14,10,8.若这三天中至少有一天开车上班的职工人数是20,则这三天都开车上班的职工人数至多是 .
6.(2024·黑龙江哈尔滨·一模)设表示不超过的正整数集合,表示k个元素的有限集,表示集合A中所有元素的和,集合,则 ;若,则m的最大值为 .
反思提升:
1.进行集合运算时,首先看集合能否化简,能化简的先化简,再研究其关系并进行运算.
2.数形结合思想的应用:
(1)离散型数集或抽象集合间的运算,常借助Venn图求解;
(2)连续型数集的运算,常借助数轴求解,运用数轴时要特别注意端点是实心还是空心.
分层检测
【基础篇】
一、单选题
1.(2023·重庆·三模)已知集合,,则下列关系正确的是( )
A.B.C.D.
2.(2024·浙江·二模)已知集合,,若,则满足集合的个数为( )
A.4B.6C.7D.8
3.(2024·全国·模拟预测)若集合,则( )
A.B.
C.D.
4.(2024·贵州贵阳·模拟预测)若集合,其中且,则实数m的取值范围是( )
A.B.C.D.
二、多选题
5.(2024·广西·二模)若集合和关系的Venn图如图所示,则可能是( )
A.
B.
C.
D.
6.(20-21高一上·广东深圳·阶段练习)1872年德国数学家戴德金从连续性的要求出发,用有理数的“分割”来定义无理数(史称“戴德金分割”),并把实数理论建立在严格的科学基础上,从而结束了无理数被认为“无理”的时代,也结束了数学史上的第一次大危机.将有理数集划分为两个非空的子集与,且满足中的每一个元素都小于中的每一个元素,则称为戴德金分割.试判断下列选项中,可能成立的是( )
A.若,则满足戴德金分割
B.若为戴德金分割,则没有最大元素,有一个最小元素
C.若为戴德金分割,则有一个最大元素,有一个最小元素
D.若为戴德金分割,则没有最大元素,也没有最小元素
7.(23-24高一上·重庆永川·期中)下列说法正确的是( )
A.集合,,,若则或
B.设全集为,若,则
C.集合
D.“和都是无理数”是“是无理数”的必要不充分条件
三、填空题
8.(23-24高三下·上海浦东新·阶段练习)已知集合,全集,则 .
9.(2024·山东临沂·一模)集合,,则 .
10.(2020·江苏·一模)若,,则下图中阴影表示的集合为 .
四、解答题
11.(2023·河南·模拟预测)设集合,
.
(1)求;
(2)从下面(1)(2)中选择一个作为已知条件,求实数的取值范围.
①;②;③.
注:如果选择多个条件分别解答,按第一个解答计分.
12.(2023·黑龙江佳木斯·模拟预测)已知集合,集合.
(1)若,求实数m的取值范围;
(2)命题,命题,若p是q成立的充分不必要条件,求实数m的取值范围.
【能力篇】
一、单选题
1.(2023·四川·模拟预测)已知集合,则( )
A.B.C.D.
二、多选题
2.(2022·河北衡水·模拟预测)将函数的图象向左平移个单位,得到函数的图象,若在上为增函数,则的值可能为( )
A.B.2C.3D.4
三、填空题
3.(2024·河南·模拟预测)已知集合,若,则的最小值为 .
四、解答题
4.(2023·河南·模拟预测)已知数列是首项为1的等差数列,数列是公比为2的等比数列,且.
(1)求数列的通项公式;
(2)设表示不超过的最大整数(如:),求集合中元素的个数.
【培优篇】
一、单选题
1.(2023·上海普陀·一模)设、、、、是均含有个元素的集合,且,,记,则中元素个数的最小值是( )
A.B.C.D.
二、多选题
2.(21-22高三上·江苏徐州·阶段练习)函数的定义域为,值域为,下列结论中一定成立的结论的序号是( )
A.B.C.D.
三、填空题
3.(2022·上海青浦·二模)已知集合,其中且,函数,且对任意,都有,则的值是
成套的课件成套的教案成套的试题成套的微专题尽在高中数学同步资源大全QQ群552511468也可联系微信fjshuxue加入百度网盘群1.5T一线老师必备资料一键转存自动更新永不过期
名称
自然数集
正整数集
整数集
有理数集
实数集
记法
N
N*或N+
Z
Q
R
集合的并集
集合的交集
集合的补集
符号表示
A∪B
A∩B
若全集为U,则集合A的补集为∁UA
图形表示
集合表示
{x|x∈A,或x∈B}
{x|x∈A,且x∈B}
{x|x∈U,且x∉A}
专题01 集合(新高考专用)
目录
【知识梳理】2
【真题自测】3
【考点突破】8
【考点1】集合的基本概念8
【考点2】集合间的基本关系11
【考点3】集合的运算14
【分层检测】18
【基础篇】18
【能力篇】25
【培优篇】28
考试要求:
1.了解集合的含义,理解元素与集合的属于关系,能在自然语言、图形语言的基础上,用符号语言刻画集合.
2.理解集合间包含与相等的含义,能识别给定集合的子集.
3.在具体情境中,了解全集与空集的含义.
4.理解两个集合的并集、交集与补集的含义,会求两个简单集合的并集、交集与补集.
5.能使用Venn图表达集合间的基本关系与基本运算.
知识梳理
1.元素与集合
(1)集合中元素的三个特性:确定性、互异性、无序性.
(2)元素与集合的关系是属于或不属于,表示符号分别为∈和∉.
(3)集合的三种表示方法:列举法、描述法、图示法.
(4)常用数集及记法
2.集合间的基本关系
(1)子集:一般地,对于两个集合A,B,如果集合A中任意一个元素都是集合B中的元素,就称集合A为集合B的子集.记作A⊆B(或B⊇A).
(2)真子集:如果集合A⊆B,但存在元素x∈B,且x∉A,就称集合A是集合B的真子集,记作AB(或BA).
(3)相等:若A⊆B,且B⊆A,则A=B.
(4)空集的性质:∅是任何集合的子集,是任何非空集合的真子集.
3.集合的基本运算
4.集合的运算性质
(1)A∩A=A,A∩∅=∅,A∩B=B∩A.
(2)A∪A=A,A∪∅=A,A∪B=B∪A.
(3)A∩(∁UA)=∅,A∪(∁UA)=U,∁U(∁UA)=A.
1.若有限集A中有n个元素,则A的子集有2n个,真子集有2n-1个,非空子集有2n-1个,非空真子集有2n-2个.
2.注意空集:空集是任何集合的子集,是非空集合的真子集.
3.A⊆B⇔A∩B=A⇔A∪B=B⇔∁UA⊇∁UB.
4.∁U(A∩B)=(∁UA)∪(∁UB),∁U(A∪B)=(∁UA)∩(∁UB).
真题自测
一、单选题
1.(2023·全国·高考真题)设全集,集合,( )
A.B.
C.D.
2.(2023·全国·高考真题)已知等差数列的公差为,集合,若,则( )
A.-1B.C.0D.
3.(2023·全国·高考真题)设集合,集合,,则( )
A.B.
C.D.
4.(2023·全国·高考真题)已知集合,,则( )
A.B.C.D.
5.(2023·全国·高考真题)设集合,,若,则( ).
A.2B.1C.D.
6.(2022·全国·高考真题)已知集合,则( )
A.B.C.D.
7.(2022·全国·高考真题)设全集,集合,则( )
A.B.C.D.
8.(2022·全国·高考真题)设全集,集合M满足,则( )
A.B.C.D.
9.(2022·全国·高考真题)若集合,则( )
A.B.C.D.
10.(2021·全国·高考真题)设集合,则( )
A.B.C.D.
11.(2021·全国·高考真题)已知集合,,则( )
A.B.C.D.
12.(2021·全国·高考真题)设集合,则( )
A.B.
C.D.
参考答案:
1.A
【分析】根据整数集的分类,以及补集的运算即可解出.
【详解】因为整数集,,所以,.
故选:A.
2.B
【分析】
根据给定的等差数列,写出通项公式,再结合余弦型函数的周期及集合只有两个元素分析、推理作答.
【详解】
依题意,等差数列中,,
显然函数的周期为3,而,即最多3个不同取值,又,
则在中,或,
于是有,即有,解得,
所以,.
故选:B
3.A
【分析】由题意逐一考查所给的选项运算结果是否为即可.
【详解】由题意可得,则,选项A正确;
,则,选项B错误;
,则或,选项C错误;
或,则或,选项D错误;
故选:A.
4.C
【分析】方法一:由一元二次不等式的解法求出集合,即可根据交集的运算解出.
方法二:将集合中的元素逐个代入不等式验证,即可解出.
【详解】方法一:因为,而,
所以.
故选:C.
方法二:因为,将代入不等式,只有使不等式成立,所以.
故选:C.
5.B
【分析】
根据包含关系分和两种情况讨论,运算求解即可.
【详解】因为,则有:
若,解得,此时,,不符合题意;
若,解得,此时,,符合题意;
综上所述:.
故选:B.
6.B
【分析】方法一:求出集合后可求.
【详解】[方法一]:直接法
因为,故,故选:B.
[方法二]:【最优解】代入排除法
代入集合,可得,不满足,排除A、D;
代入集合,可得,不满足,排除C.
故选:B.
【整体点评】方法一:直接解不等式,利用交集运算求出,是通性通法;
方法二:根据选择题特征,利用特殊值代入验证,是该题的最优解.
7.D
【分析】解方程求出集合B,再由集合的运算即可得解.
【详解】由题意,,所以,
所以.
故选:D.
8.A
【分析】先写出集合,然后逐项验证即可
【详解】由题知,对比选项知,正确,错误
故选:
9.D
【分析】求出集合后可求.
【详解】,故,
故选:D
10.B
【分析】根据交集、补集的定义可求.
【详解】由题设可得,故,
故选:B.
11.C
【分析】分析可得,由此可得出结论.
【详解】任取,则,其中,所以,,故,
因此,.
故选:C.
12.B
【分析】根据交集定义运算即可
【详解】因为,所以,
故选:B.
【点睛】本题考查集合的运算,属基础题,在高考中要求不高,掌握集合的交并补的基本概念即可求解.
考点突破
【考点1】集合的基本概念
一、单选题
1.(2023·江苏·一模)设,,则( )
A.B.C.D.
2.(2023·北京海淀·模拟预测)设集合,若,则实数m=( )
A.0B.C.0或D.0或1
二、多选题
3.(22-23高一下·湖南邵阳·开学考试)若对任意,,则称为“影子关系”集合,下列集合为“影子关系”集合的是( )
A.B.C.D.
4.(2021·全国·模拟预测)设集合,若,,,则运算可能是( )
A.加法B.减法C.乘法D.除法
三、填空题
5.(2024·辽宁葫芦岛·一模)已知集合,.若,则实数的取值集合为 .
6.(2023·湖北·二模)已知X为包含v个元素的集合(,).设A为由X的一些三元子集(含有三个元素的子集)组成的集合,使得X中的任意两个不同的元素,都恰好同时包含在唯一的一个三元子集中,则称组成一个v阶的Steiner三元系.若为一个7阶的Steiner三元系,则集合A中元素的个数为 .
参考答案:
1.B
【分析】分别分析两个集合中的元素所代表的意思即可判断选项.
【详解】解:因为,因为,
所以集合是由所有奇数的一半组成,
而集合是由所有整数的一半组成,故.
故选:B
2.C
【分析】根据元素与集合的关系,分别讨论和两种情况,求解并检验集合的互异性,可得到答案.
【详解】设集合,若,
,或,
当时,,此时;
当时,,此时;
所以或.
故选:C
3.ABD
【分析】根据“影子关系”集合的定义逐项分析即可.
【详解】根据“影子关系”集合的定义,
可知,,为“影子关系”集合,
由,得或,当时,,故不是“影子关系”集合.
故选:ABD
4.AC
【分析】先由题意设出,,然后分别计算,,,,即可得解.
【详解】由题意可设,,其中,,,,
则,,所以加法满足条件,A正确;,当时,,所以减法不满足条件,B错误;
,,所以乘法满足条件,C正确;,当时,,所以除法不满足条件,D错误.
故选:AC.
5.
【分析】
根据,得到集合的元素都是集合的元素,即可求得的值.
【详解】由题意,所以或,则或,
所以实数的取值集合为.
故答案为:.
6.7
【分析】令,列举出所有三元子集,结合组成v阶的Steiner三元系定义,确定中元素个数.
【详解】由题设,令集合,共有7个元素,
所以的三元子集,如下共有35个:
、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、,
因为中集合满足X中的任意两个不同的元素,都恰好同时包含在唯一的一个三元子集,所以中元素满足要求的有:
、、、、、、,共有7个;
、、、、、、,共有7个;
、、、、、、,共有7个;
、、、、、、,共有7个;
、、、、、、,共有7个;
、、、、、、,共有7个;
、、、、、、,共有7个;
、、、、、、,共有7个;
、、、、、、,共有7个;
、、、、、、,共有7个;
、、、、、、,共有7个;
、、、、、、,共有7个;
、、、、、、,共有7个;
、、、、、、,共有7个;
、、、、、、,共有7个;
共有15种满足要求的集合A,但都只有7个元素.
故答案为:7
反思提升:
1.研究集合问题时,首先要明确构成集合的元素是什么,即弄清该集合是数集、点集,还是其他集合;然后再看集合的构成元素满足的限制条件是什么,从而准确把握集合的含义.
2.利用集合元素的限制条件求参数的值或确定集合中元素的个数时,要注意检验集合中的元素是否满足互异性.
【考点2】集合间的基本关系
一、单选题
1.(2024·全国·模拟预测)若集合,,则集合的真子集的个数为( )
A.0B.1C.2D.3
2.(2024·全国·模拟预测)已知集合,.若,则的取值范围是( )
A.B.
C.D.
二、多选题
3.(23-24高一上·陕西西安·期中)下列说法正确的是( )
A.
B.集合
C.函数的值域为
D.在定义域内单调递增
4.(2024·甘肃定西·一模)设集合,则( )
A.
B.的元素个数为16
C.
D.的子集个数为64
三、填空题
5.(2024·全国·模拟预测)已知全集,集合,.若,则的最大值为 .
6.(2021·山东淄博·模拟预测)已知数列为等差数列,数列为等比数列.若集合,集合,集合(,),且,则 .
参考答案:
1.D
【分析】先求集合A,确定即可求解.
【详解】因为,,所以,
所以集合的真子集的个数为.
故选:D.
2.D
【分析】根据对数函数单调性求集合A,由题意可知,即可得结果.
【详解】由题意可得,
因为,则,所以.
故选:D.
3.BD
【分析】根据空集的定义判断A,根据集合元素的特征判断B,根据所给函数解析式判断C,将函数写成分段函数、再分析函数在各段的单调性即可判断D.
【详解】对于A:或,故A错误;
对于B:,
又,令,所以,,
即,
所以,故B正确;
对于C:因为,所以的值域为,故C错误;
对于D:,
因为在上单调递增,在上单调递增,
且为连续函数,所以在上单调递增,故D正确;
故选:BD
4.BCD
【分析】解二次不等式化简集合,进而求得集合,利用集合的交并运算与常用数集的定义,结合集合子集个数的求法逐一分析各选项即可得解.
【详解】对于ABC,因为,
所以,即,
所以有个元素,故A错误,BC正确;
对于D,而有个元素,所以的子集个数为,故D正确.
故选:BCD.
5.
【分析】先求集合,对分类讨论,并结合,数形结合求出的取值范围,注意端点值能否取到.
【详解】因为,
当时,,若,则.
在数轴上表示出集合,,如图,
则;
当时,,此时不成立,
当时,,此时不成立.
综上,的最大值为.
故答案为:
6.5
【解析】根据题意判断出,根据等比数列的性质可得,根据等差数列的性质,列出等式(或),求出即可.
【详解】由,其中,,
可得,则,令,或可得,①
令中的,根据等差数列的性质可得,
所以,②
根据①②得出,所以;
令中的,根据等差数列的性质可得,
所以,③
根据①③得出,所以;
同理令中的,根据等差数列的性质可得,
所以,与①联立可;
令中的,根据等差数列的性质可得,
所以,与①联立可;综上所述.
故答案为:.
【点睛】本题主要考查等差数列、等比数列的性质与集合相等,关键点是判断出,根据等比数列的性质可得,根据等差数列的性质,列出等式(或),考查学生分析问题、解决问题的能力.
反思提升:
1.若B⊆A,应分B=∅和B≠∅两种情况讨论.
2.已知两个集合间的关系求参数时,关键是将两个集合间的关系转化为元素或区间端点间的关系,进而求得参数范围.注意合理利用数轴、Venn图帮助分析及对参数进行讨论.求得参数后,一定要把端点值代入进行验证,否则易增解或漏解.
【考点3】集合的运算
一、单选题
1.(2024·全国·模拟预测)已知集合,,则( )
A.B.C.D.
2.(2024·全国·模拟预测)已知集合,,则( )
A.B.C.D.
二、多选题
3.(2022·重庆·模拟预测)已知全集,集合,则关于的表达方式正确的有( )
A.B.
C.D.
4.(23-24高三上·海南省直辖县级单位·阶段练习)图中阴影部分所表示的集合是( )
A.B.C.D.
三、填空题
5.(2020·江苏南通·模拟预测)某单位周一、周二、周三开车上班的职工人数分别是14,10,8.若这三天中至少有一天开车上班的职工人数是20,则这三天都开车上班的职工人数至多是 .
6.(2024·黑龙江哈尔滨·一模)设表示不超过的正整数集合,表示k个元素的有限集,表示集合A中所有元素的和,集合,则 ;若,则m的最大值为 .
参考答案:
1.C
【分析】解绝对值不等式求出集合,求函数的定义域求得集合.由此求出,从而得到.
【详解】由题意,得,,所以,所以.
故选:C.
2.B
【分析】首先解对数不等式求出集合,再解一元二次不等式求出集合,最后根据并集的定义计算可得.
【详解】由得,解得,
所以.
由解得,即,
所以.
故选:B.
3.AB
【分析】根据补集的概念及分式不等式及其解法即可求解.
【详解】由题意得,,
所以,
故AB正确,CD错误,
故选:AB.
4.AC
【分析】利用维恩图,根据交并补的混合运算即可得到答案.
【详解】如图,
对于A,,则,故A正确;
对于B,,则,故B错误;
对于C,,,故,故C正确;
对于D,,故D错误,
故选:AC.
5.6
【分析】将原问题转化为Venn图的问题,然后结合题意确定这三天都开车上班的职工人数至多几人即可.
【详解】如图所示,(a+b+c+x)表示周一开车上班的人数,(b+d+e+x)表示周二开车上班人数,(c+e+f+x)表示周三开车上班人数,x表示三天都开车上班的人数,
则有:
,
即,
即,当时,x的最大值为6,
即三天都开车上班的职工人数至多是6.
故答案为:6
【点睛】本题主要考查Venn图的应用,数形结合的数学思想等知识,意在考查学生的转化能力和计算求解能力.
6. 22
【分析】
根据定义,结合等差数列的前项和公式进行求解即可.
【详解】
当时,表示有2个元素的集合,,
因为,且有2个元素,
所以或或,所以;
由题中定义可知:,
于是由
,
而,
即,又因为,
所以m的最大值为,
故答案为:;
【点睛】
关键点睛:本题的关键是理解题中定义,运用等差数列的前项和公式.
反思提升:
1.进行集合运算时,首先看集合能否化简,能化简的先化简,再研究其关系并进行运算.
2.数形结合思想的应用:
(1)离散型数集或抽象集合间的运算,常借助Venn图求解;
(2)连续型数集的运算,常借助数轴求解,运用数轴时要特别注意端点是实心还是空心.
分层检测
【基础篇】
一、单选题
1.(2023·重庆·三模)已知集合,,则下列关系正确的是( )
A.B.C.D.
2.(2024·浙江·二模)已知集合,,若,则满足集合的个数为( )
A.4B.6C.7D.8
3.(2024·全国·模拟预测)若集合,则( )
A.B.
C.D.
4.(2024·贵州贵阳·模拟预测)若集合,其中且,则实数m的取值范围是( )
A.B.C.D.
二、多选题
5.(2024·广西·二模)若集合和关系的Venn图如图所示,则可能是( )
A.
B.
C.
D.
6.(20-21高一上·广东深圳·阶段练习)1872年德国数学家戴德金从连续性的要求出发,用有理数的“分割”来定义无理数(史称“戴德金分割”),并把实数理论建立在严格的科学基础上,从而结束了无理数被认为“无理”的时代,也结束了数学史上的第一次大危机.将有理数集划分为两个非空的子集与,且满足中的每一个元素都小于中的每一个元素,则称为戴德金分割.试判断下列选项中,可能成立的是( )
A.若,则满足戴德金分割
B.若为戴德金分割,则没有最大元素,有一个最小元素
C.若为戴德金分割,则有一个最大元素,有一个最小元素
D.若为戴德金分割,则没有最大元素,也没有最小元素
7.(23-24高一上·重庆永川·期中)下列说法正确的是( )
A.集合,,,若则或
B.设全集为,若,则
C.集合
D.“和都是无理数”是“是无理数”的必要不充分条件
三、填空题
8.(23-24高三下·上海浦东新·阶段练习)已知集合,全集,则 .
9.(2024·山东临沂·一模)集合,,则 .
10.(2020·江苏·一模)若,,则下图中阴影表示的集合为 .
四、解答题
11.(2023·河南·模拟预测)设集合,
.
(1)求;
(2)从下面(1)(2)中选择一个作为已知条件,求实数的取值范围.
①;②;③.
注:如果选择多个条件分别解答,按第一个解答计分.
12.(2023·黑龙江佳木斯·模拟预测)已知集合,集合.
(1)若,求实数m的取值范围;
(2)命题,命题,若p是q成立的充分不必要条件,求实数m的取值范围.
参考答案:
1.B
【分析】根据数集的定义,求解方程,得出集合,即可得出答案.
【详解】若,解可得,或或,
所以.
若,则,所以,
所以.
故选:B.
2.D
【分析】根据包含关系,写出所有满足条件的集合A即可得解.
【详解】因为,
所以可以是,共8个,
故选:D
3.D
【分析】根据一元二次不等式的解集确定集合,根据对数函数的定义域确定集合,再根据集合的交集运算得结果.
【详解】因为集合,
则.
故选:D.
4.A
【分析】借助元素与集合的关系计算即可得.
【详解】由题意可得,解得.
故选:A.
5.ACD
【分析】根据Venn图可知,依次判定选项即可.
【详解】根据Venn图可知,
对于A,显然,故A正确;
对于B,,则,故B错误;
对于C,,则,故C正确;
对于D,,或,
则,故D正确.
故选:ACD
6.BD
【分析】A选项,,A错;BD选项,可举出例子;C选项,推理出,C错误.
【详解】A选项,,故,A错误;
B选项,设,满足,
此时为戴德金分割,且没有最大元素,有一个最小元素,B正确;
C选项,若有一个最大元素,有一个最小元素,则,故C错误;
D选项,设,满足没有最大元素,也没有最小元素,D正确.
故选:BD
7.BC
【分析】对于A:由,得出或等于2,分别求解,然后验证互异性即可判断为错;对于B:由集合间的包含关系和补集的概念判断正确;对于C:令集合中的,即可判定为正确;对于D,取特值即可判定为错误.
【详解】对于A:由,
若或1,
当时,不满足互异性,舍去,当时,,不满足互异性,舍去;
若或2,
当时,合题意,当时,,合题意,
故或2,A错误;
对于B:若,则,B正确;
对于C:令集合中的,得,故C正确;
对于D:不是无理数,若为无理数,可取,和不都是无理数,故“和都是无理数”是“是无理数”的既不充分也不必要条件,故D错.
故选:BC.
8.
【分析】利用集合的补集求解.
【详解】解:集合,全集,
所以,
故答案为:
9.
【分析】首先解对数不等式求出集合,再解分式不等式求出集合,最后根据补集、交集的定义计算可得.
【详解】由,可得,则,
所以,
由,可得,等价于,解得,
所以,
所以,所以.
故答案为:
10.
【分析】根据韦恩图表示的是,再利用交集的定义计算即可.
【详解】解:韦恩图表示的是,由,,则.
故答案为:
【点睛】本题考查交集的运算,韦恩图的应用,属于基础题.
11.(1);
(2)答案见解析
【分析】(1)解不等式结合集合的运算计算即可;
(2)结合所选条件判定集合间的关系,注意分类讨论解含参不等式一一计算即可.
【详解】(1)由,得,
由,即,
所以;
(2)因为的两根分别为,
若选择①,由(1)得,,故.
当,即时,,满足题意;
当,即时,,
由,得,解得,所以;
当,即时,,不满足.
综上可知,实数的取值范围为.
若选择②,由(1)得,,故,
当,即时,,满足题意;
当,即时,,
由,得,解得,所以;
当,即时,,
由,得,解得,所以.
综上可知,实数的取值范围为.
若选择③,由(1)得,
当,即时,,满足题意;
当,即时,,此时成立,
满足题意,所以;
当,即时,,显然不满足.
综上可知,实数的取值范围为.
12.(1)
(2)
【分析】(1)根据一元二次不等式化简,即可由交集为空集,分情况讨论,
(2)根据真子集,即可列不等式求解.
【详解】(1)由得,
由,
①若,即时,,符合题意;
②若,即时,需或,解得.
综上,实数m的取值范围为.
(2)由已知A是B的真子集,知,且两个端点不同时取等号,解得.
由实数m的取值范围为.
【能力篇】
一、单选题
1.(2023·四川·模拟预测)已知集合,则( )
A.B.C.D.
二、多选题
2.(2022·河北衡水·模拟预测)将函数的图象向左平移个单位,得到函数的图象,若在上为增函数,则的值可能为( )
A.B.2C.3D.4
三、填空题
3.(2024·河南·模拟预测)已知集合,若,则的最小值为 .
四、解答题
4.(2023·河南·模拟预测)已知数列是首项为1的等差数列,数列是公比为2的等比数列,且.
(1)求数列的通项公式;
(2)设表示不超过的最大整数(如:),求集合中元素的个数.
参考答案:
1.A
【分析】根据列举法求解集合和求解一元二次不等式的解法即可求解.
【详解】,
若要,
则需,
所以解得
所以,
所以.
故选:.
2.AB
【分析】根据给定条件求出函数的解析式,进而求出的含有数0的单调区间,再借助集合的包含关系列式作答.
【详解】依题意,,由,得:,
于是得的一个单调递增区间是,因在上为增函数,
因此,,即有,解得,
所以,选项C,D不满足,选项A,B满足.
故选:AB
3.
【分析】由可得,解出集合后结合集合的关系计算即可得.
【详解】由,故,
由,得,
故有,即,即,
即的最小值为.
故答案为:.
4.(1)
(2)36
【分析】(1)设出公差,得到方程组,求出公差和,从而得到数列的通项公式;
(2)先得到,进而求出当时,,又,故,依次类推,直至当时,,故,结合集合中的元素互异,求出集合中元素个数.
【详解】(1)设等差数列的公差为,
由题意可知,
因为,
所以,
解得,所以,
,故.
(2)因为,所以,所以.
因为,
所以当时,,则,又,故;
当时,,则,故;
当时,,则,故;
当时,,则,故,
依次类推,当时,,则,故,
由于集合中的元素互异,需要减去重复出现的元素,
所以集合中元素的个数为
个.
【培优篇】
一、单选题
1.(2023·上海普陀·一模)设、、、、是均含有个元素的集合,且,,记,则中元素个数的最小值是( )
A.B.C.D.
二、多选题
2.(21-22高三上·江苏徐州·阶段练习)函数的定义域为,值域为,下列结论中一定成立的结论的序号是( )
A.B.C.D.
三、填空题
3.(2022·上海青浦·二模)已知集合,其中且,函数,且对任意,都有,则的值是 .
参考答案:
1.A
【分析】设、、、是集合互不相同的元素,分析可知,然后对的取值由小到大进行分析,验证题中的条件是否满足,即可得解.
【详解】解:设、、、是集合互不相同的元素,若,则,不合乎题意.
①假设集合中含有个元素,可设,则,
,这与矛盾;
②假设集合中含有个元素,可设,,
,,,满足题意.
综上所述,集合中元素个数最少为.
故选:A.
【点睛】关键点点睛:本题考查集合元素个数的最值的求解,解题的关键在于对集合元素的个数由小到大进行分类,对集合中的元素进行分析,验证题中条件是否成立即可.
2.ACD
【分析】先研究值域为时函数的定义域,再研究使得值域为得函数的最小值的自变量的取值集合,研究函数值取1,2时对应的自变量的取值,由此可判断各个选项.
【详解】由于,
,,,,
即函数的定义域为
当函数的最小值为1时,仅有满足,所以,故D正确;
当函数的最大值为2时,仅有满足,所以,故C正确;
即当时,函数的值域为,故,故不一定正确,故A正确,B错误;
故选:ACD
【点睛】关键点睛:本题考查函数的定义域及其求法,解题的关键是通过函数的值域求出函数的定义域,再利用元素与集合关系的判断,集合的包含关系判断,考查了学生的逻辑推理与转化能力,属于基础题.
3.或3.
【分析】先判断区间与的关系可得,再分析时定义域与值域的关系,根据函数的单调性可确定定义域与值域的区间端点的不等式,进而求得和即可.最后分析当时,,从而确定定义域与值域的关系,列不等式求解即可
【详解】先判断区间与的关系,因为,故或.因为当,即时,由题意,当时,,故不成立;故.
再分析区间与的关系,因为,故或.
①当,即时,因为在区间上为减函数,故当, ,因为,而,故此时,即,因为,故即,故,解得,因为,故.此时区间在左侧,在右侧.故当时,,因为,故,所以 ,此时,故,解得,因为,故;
②当时,在区间上单调递减,易得,故此时且,即且,所以,故,故,即,,因为,故;
综上所述,或3
故答案为:或3
成套的课件成套的教案成套的试题成套的微专题尽在高中数学同步资源大全QQ群552511468也可联系微信fjshuxue加入百度网盘群1.5T一线老师必备资料一键转存自动更新永不过期
名称
自然数集
正整数集
整数集
有理数集
实数集
记法
N
N*或N+
Z
Q
R
集合的并集
集合的交集
集合的补集
符号表示
A∪B
A∩B
若全集为U,则集合A的补集为∁UA
图形表示
集合表示
{x|x∈A,或x∈B}
{x|x∈A,且x∈B}
{x|x∈U,且x∉A}
2025年高考数学一轮复习讲义(知识梳理+真题自测+考点突破+分层检测)专题47椭圆(新高考专用)(原卷版+解析): 这是一份2025年高考数学一轮复习讲义(知识梳理+真题自测+考点突破+分层检测)专题47椭圆(新高考专用)(原卷版+解析),共56页。
2025年高考数学一轮复习讲义(知识梳理+真题自测+考点突破+分层检测)专题43直线的方程(新高考专用)(原卷版+解析): 这是一份2025年高考数学一轮复习讲义(知识梳理+真题自测+考点突破+分层检测)专题43直线的方程(新高考专用)(原卷版+解析),共47页。
2025年高考数学一轮复习讲义(知识梳理+真题自测+考点突破+分层检测)专题35数列求和(新高考专用)(原卷版+解析): 这是一份2025年高考数学一轮复习讲义(知识梳理+真题自测+考点突破+分层检测)专题35数列求和(新高考专用)(原卷版+解析),共52页。












