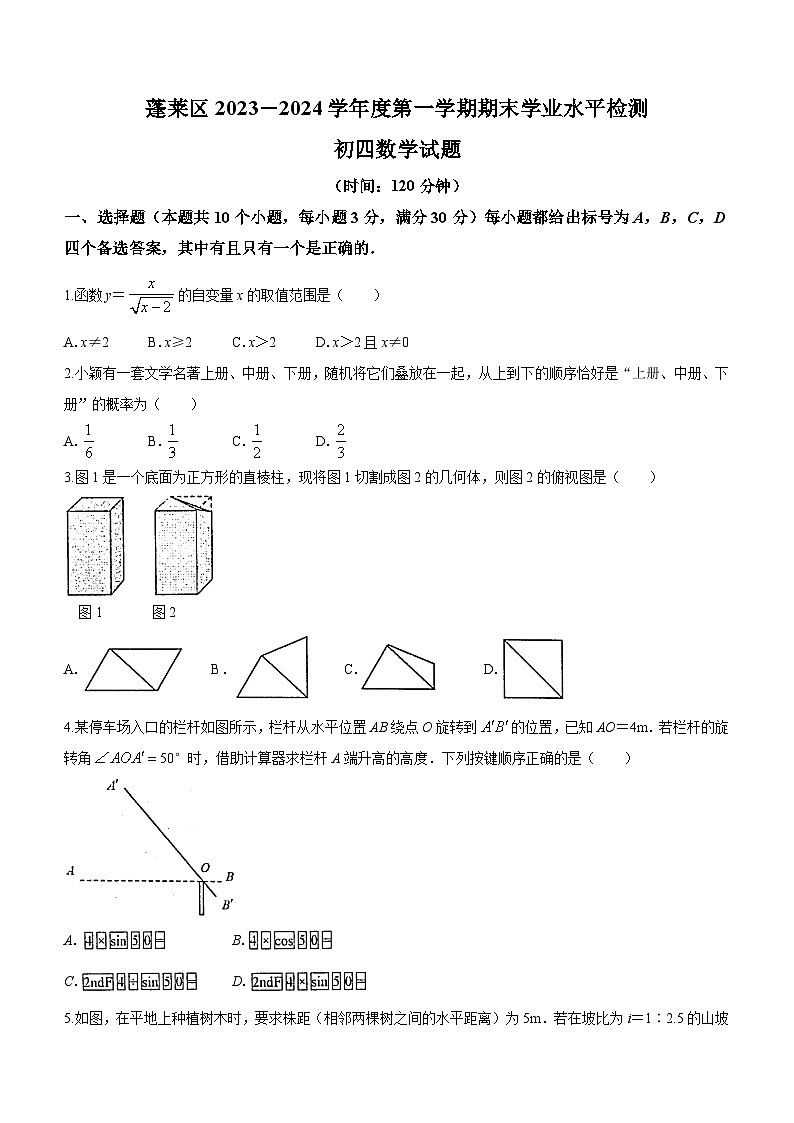
2023-2024学年山东省烟台市蓬莱区九年级（上）期末数学试卷（五四学制）

这是一份2023-2024学年山东省烟台市蓬莱区九年级（上）期末数学试卷（五四学制），共15页。试卷主要包含了填空题，解答题等内容，欢迎下载使用。
（时间：120分钟）
一、选择题（本题共10个小题，每小题3分，满分30分）每小题都给出标号为A，B，C，D四个备选答案，其中有且只有一个是正确的．
1.函数y＝的自变量x的取值范围是（ ）
A.x≠2B.x≥2C.x＞2D.x＞2且x≠0
2.小颖有一套文学名著上册、中册、下册，随机将它们叠放在一起，从上到下的顺序恰好是“上册、中册、下册”的概率为（ ）
A.B.C.D.
3.图1是一个底面为正方形的直棱柱，现将图1切割成图2的几何体，则图2的俯视图是（ ）
图1 图2
A. B．C.D.
4.某停车场入口的栏杆如图所示，栏杆从水平位置AB绕点O旋转到的位置，已知AO＝4m．若栏杆的旋转角50°时，借助计算器求栏杆A端升高的高度．下列按键顺序正确的是（ ）
A.B.
C.D.
5.如图，在平地上种植树木时，要求株距（相邻两棵树之间的水平距离）为5m．若在坡比为i＝1∶2.5的山坡上种树，也要求株距为5m，那么相邻两棵树间的坡面距离为（ ）
B.5mC.mD.10m
6.将矩形纸片ABCD如图所示进行裁剪，所裁剪出的扇形与圆刚好能够做成一个圆锥．若BC＝9cm，则AB的长为（ ）
A.5cmC.6cmD.7cm
7.函数y＝与y＝－k2＋k在同一直角坐标系中的图象可能是（ ）
A.B.C.D.
8.某仿古墙上原有一个矩形的窗洞，现要将它改为一个圆弧形的窗洞，圆弧所在的圆外接于矩形，如图．已知矩形的宽为1m，高为m，则改建后窗洞的圆弧长是（ ）
A.B.C.D.
9.下列有关圆的一些结论：
①任意三点可以确定一个圆；
②相等的圆心角所对的弧相等；
③平分弦的直径垂直于弦，并且平分弦所对的弧；
= 4 \* GB3 ④圆内接四边形对角互补；
⑤三角形的外心到三角形三个顶点的距离都相等；
⑥直角三角形的内心在斜边的中点上．
正确的个数是（ ）
A.1个B.2个C.3个D.4个
10.如图，△ABC是等腰直角三角形，∠A＝90°，AB＝6，点P是AB边上一动点（点P与点A重合），以AP为边作正方形APDE，设AP＝x，正方形APDE与△ABC重合部分（阴影部分）的面积为y则下列能大致反映y与x的函数关系的图象是（ ）
A.B.C.D.
二、填空题（本题共6个小题，每小题3分，满分18分）
11.在△ABC中，∠A、∠B均为锐角，且，则△ABC的形状为 ．
12.二次函数y＝ax2＋bx＋c （a≠0），经过点（1，0），对称轴l如图所示，若M＝a＋b－c，N＝2a－b，P＝a＋c，则M，N，P中，值小于0的数有 ．
13.烟台高铁南站段修建过程中需要经过一座小山．如图，施工方计划沿AC方向开挖隧道，为了加快施工速度，要在小山的另一侧D（A，C，D共线）处同时施工，测得∠CAB＝30°，AB＝4km，∠ABD＝105°，则BD的长为 ．
14.如图，是由一个大圆和四个相同的小圆组成的如图所示的图案，若小圆的半径为2，则阴影部分的面积为 ．
15.如图，一次函数y＝2x与反比例函数y＝的图象交于A，B两点，动点M在以C（2，0）为圆心，半径为1的⊙C上，N是AM的中点，已知ON长的最大值为，则k的值为 ．
16.如图，在△ABC中，点P从点A出发向点C运动，在运动过程中，设x表示线段AP的长，y表示线段BP的长，y与x之间的函数关系如图②所示，其中，L为曲线部分的最低点，则△ABC的面积为 ．

图 = 1 \* GB3 ① 图②
三、解答题（本大题共9个题，满分72分．解答题要写出必要的计算步骤或文字说明或说理过程）
17.（本题满分6分）先化简，再求值：，其中．
18.（本题满分7分）如图，有四张背面完全相同的卡片A，B，C，D，其中正面分别写着四个不同的函数表达式，将四张卡片洗匀正面朝下随机放在桌面上．
（1）从四张卡片中随机摸出一张，摸出的卡片上的函数y随x的增大而减小的概率是 ；
（2）小亮和小强用这四张卡片做游戏，规则如下：两人同时从四张卡片中各随机抽出一张，若抽出的两张卡片上的函数增减性相同，则小亮胜；若抽出的两张卡片上的函数增减性不同，则小强胜．这个游戏公平吗？请说明理由．
19.（本题满分7分）我国非常重视职业教育，某职业技术学校开设：A（旅游管理）、B（信息技术）、C（酒店管理）、D（汽车维修）四个专业．为了解中学生对这些专业的喜爱程度，特进行了随机抽样调查，每个被调查的学生从这四个专业中选择一个且只能选择一个，调查结果绘制成如下两幅不完整的统计图．
根据图中信息，解答下列问题：
（1）本次被调查的学生有 人；
（2）统计图中D（汽车维修）专业所对应的圆心角的度数为 ，请补全条形统计图；
（3）从选择D（汽车维修）专业的甲、乙、丙、丁四名同学中随机抽取两人去某汽车维修店观摩学习．请用列表法或画树状图的方法求出恰好抽到甲、乙两名同学的概率．
20.（本题满分7分）如图，一个零件形如一个圆柱体削去底面圆的四分之一部分的柱体，底面圆的半径为2cm．
（1）请画出该零件的三视图；
（2）若用该零件的俯视图围成一个圆锥，求这个圆锥的高．
21.（本题满分7分）如图，希望中学的教学楼AB和综合楼CD之间生长着一棵高度为12.88米的白杨树EF，且其底端B，D，F在同一直线上，BP＝FD＝40米．在综合实践活动课上，小明打算借助这棵树的高度测算出综合楼的高度，他在教学楼顶A处测得点C的仰角为9°，点E的俯角为16°．
问小明能否运用以上数据，得到综合楼的高度？若能，请求出其高度（结果精确到0.01米）；若不能，说明理由．（解答过程中可直接使用表格中的数据哟！）
22.（本题满分7分）如图，在平面直角坐标系中，⊙M与x轴的正半轴交于A、B两点，与y轴的正半轴相切于点C，连接MA、AC，已知⊙M半径为2，∠AMC＝60°，双曲线（x＞0）经过圆心M．
（1）求双曲线的解析式；
（2）求直线BC的解析式．
23.（本题满分9分）某公司营销A，B两种产品，根据市场调研，确定两条信息：
信息1：销售A种产品所获利润y（万元）与所售产品x（吨）之间存在二次函数关系，如图所示．
信息2：销售B种产品所获利润y（万元）与销售产品x（吨）之间存在正比例函数关系y＝0.3x．根据以上信息，解答下列问题：
（1）求二次函数的表达式；
（2）该公司准备购进A、B两种产品共10吨，请设计一个营销方案，使销售A、B两种产品获得的利润之和最大，最大利润是多少万元？
24.（本题满分10分）如图，AB是⊙O的直径，AC是弦，D是的中点，CD与AB交于点E．F是AB延长线上的一点，且CF为⊙O的切线．
（1）试判断线段CF与EF的数量关系，并说明理由；
（2）连接BD，取BD的中点G，连接AG．若CF＝4，BF＝2，求AG的长．
25.（本题满分12分）如图，已知抛物线y＝ax2＋bx＋c（a≠0）过点C（0，－4）．顶点为M（3，－），与x轴交于A、B两点．以AB为直径作圆，记作⊙D．
（1）求抛物线解析式及点D的坐标；
（2）猜测直线CM与⊙D的位置关系，并证明你的猜想；
（3）抛物线对称轴上是否存在点P，若将线段CP绕点P逆时针旋转90°，使点C的对应点恰好落在抛物线上？若能，求点P的坐标；若不能，说明理由．
备用图
2023－2024学年度第一学期期末学业水平考试
初四数学试题参考答案及评分建议
一、选择题（每小题3分，满分36分）
二、填空题（每小题3分，满分18分）
11.等边三角形 12. M，N 13. km 14. 15. 16.
三、解答题（共9道题，满分72分）
19.计算（本题满分6分）
解：
＝
＝ ………………………………1分
＝ ………………………………3分
x＝×＋－×＋＝＝． ………………………5分
∴原式＝． ………………………………………………6分
18.（本题满分7分）
（1） …………………………………………………………………2分
（2）不公平 ……………………………………………………………………3分
树状图或列表（略） …………………………………………………5分
抽出的两张卡片上的函数增减性相同的概率是 ；抽出的两张卡片上的函数增减性不同的概率是 ……………………………………6分
＞，∴不公平 ． ………………………………………………………7分
19.（本题满分7分）
（1）100 …………………………………………………………1分
（2）54°， …………………………………………………………………2分
补充条形统计图中，B（信息技术）专业的人数为：
100－20－35－15＝30（人） …………………………………………3分
（3）画树状图如下：
………………………………………6分
共有12种等可能的结果，其中恰好抽到甲、乙两名同学的结果有2种，
∴恰好抽到甲、乙两名同学的概率为． …………………………………7分
20.（本题满分7分）
（1）图略 …………………………………………………………3分
（2）求出圆锥底面圆的半径为 ………………………5分
求出圆锥的高为 ………………………………………………7分
21.（本题满分7分）
解：小明能运用以上数据，得到综合楼的高度， ………………………1分
理由如下：作EG⊥AB，垂足为G，作AH⊥CD，垂足为H，如图：
由题意知，EG＝ BF＝ 40米，EF＝ BG＝ 12.88米，
∠HAE＝ 16°＝ ∠AEG＝ 16°，∠CAH ＝9°， ………………………………2分
在Rt△AEG中，
tan ∠AEG＝， …………………………3分
∴tan 16°＝，
即0.287≈，
∴AG ＝ 40×0.287＝11.48（米），…………4分
∴AB ＝ AG＋BG＝11.48＋12.88＝ 24.36（米），
∴HD＝ AB ＝24.36米， ………………………………………………………5分
在Rt△ACH中，AH ＝BD＝ BF＋FD＝80米，
tan∠CAH ＝，
∴tan9°＝ ，即0.158≈，
∴CH ＝80×0.158＝ 12.64（米）， …………………………………………6分
∴CD＝CH＋HD ＝ 12.64＋24.36＝ 37.00（米），
则综合楼的高度约是37.00米． ………………………………………7分
22.（本题满分7分）
（1）如图，过点M作MN⊥x轴于N，
∴∠MNO＝90°，
∵⊙M切y轴于C，
∴∠OCM＝90°，
∵∠CON＝90°，
∴∠CON＝∠OCM＝∠ONM＝90°，
∴四边形OCMN是矩形，
∴AM＝CM＝2，∠CMN＝90°，
∵∠AMC＝60°，
∴∠AMN＝30°，
在Rt△ANM中，MN＝AM•cs∠AMN＝2× ＝ ，
∴M（2， ）， …………………………………………………………2分
∵双曲线y＝ （x＞0）经过圆心M，
∴k＝2× ＝2
∴双曲线的解析式为y＝ （x＞0）； ………………………………3分
（2）如图，过点B，C作直线，
由（1）知，四边形OCMN是矩形，
∴CM＝ON＝2，OC＝MN＝ ，
∴C（0， ）， ………………………………………………………4分
在Rt△ANM中，∠AMN＝30°，AM＝2，
∴AN＝1，
∵MN⊥AB，MN过圆心
∴BN＝AN＝1，OB＝ON＋BN＝3，
∴B（3，0）， ………………………………………………………………5分
设直线BC的解析式为y＝k'x＋b，
∴ ，
∴ ，
∴直线BC的解析式为y＝ x＋ ． ……………………………7分
23. （本题满分9分）
解：（1）根据题意，设销售A种产品所获利y与销售产品x之间的函数关系式为
………1分
将（1，1.4）、（3，3.6）代入解析式，
得： ………………2分
解得： ………………3分
∴销售A种产品获利润y与销售产品x之间的函数关系式为；……………4分
设购进A产品m吨，购进B产品（10－m）吨，
销售A、B两种产品获得的利润之和为W万元， ……………5分
则W＝， ……………6分
＝，
＝， ……………7分
∵
∴当m＝6时，W取得最大值，最大值 为6.6万元， ……………8分
答：购进A产品6吨，购进B产品4吨，销售A、B两种产品获得的利润之和最大，最大利润是6.6万元． ………………………………9分
24.（本题满分10分）
（1）FC＝F …………………………………………………………1分
证明：如图，连接OC，OD．
∵CF是⊙O的切线，
∴∠FCE＋∠OCD＝90°， ……………………2分
∵AB是直径，D是的中点，
∴∠DOE＝90°， ………………………………3分
∴∠OED＋∠ODC＝90°，
∵OC＝OD，
∴∠OCD＝∠ODC，
∴∠FCE＝∠FEC，
∴FC＝FE， ……………………………………5分
（2）解：过点G作GH⊥AB于点H． ………………………6分
设OA＝OD＝OC＝OB＝r，则OF＝r＋2，
在Rt△COF中，42＋r2＝（r＋2）2，
∴r＝3， …………………………………………………………7分
∵GH⊥AB，
∴∠GHB＝90°，
∵∠DOE＝90°，
∴∠GHB＝∠DOE，
∴GH∥DO，
∴，
∵G为BD的中点，
∴BG＝BD，
∴BH＝BO＝，GH＝OD＝， …………………………………………8分
∴AH＝AB－BH＝6－＝， …………………………………………9分
∴AG＝． ………………………10分
25.（本题满分12分）
解：（1）解：设抛物线为，
∵过点，
∴，
解得：，
∴抛物线的解析式为， ……………………………………2分
令y＝0，则，
解得：，，
∴，
∴，
∴，
∴； …………………………………………………3分
（2）连接CD，DM如图所示：
由抛物线的解析式得：，，
∵，∴

，
∴，
∴， ……………………………………………5分
∵CD＝5，则点C在圆上．
∴直线与⊙D相切； ……………………………………7分
（3）存在点P，理由如下： ……………………………………………8分
假设存在点P，设点，过点C作对称轴，过点作对称轴，则
根据题意得，
∴，
∴四边形为矩形，
∴，
∵
∴≌，
∴，
∴
∵点在抛物线上，
∴，
解得：或，
∴或． …………………………………………12分
题号
1
2
3
4
5
6
7
8
9
10
答案
C
A
D
A
C
C
A
A
B
C