辽宁省葫芦岛市兴城市2024-2025学年八年级上学期期中考试数学试卷

这是一份辽宁省葫芦岛市兴城市2024-2025学年八年级上学期期中考试数学试卷，文件包含辽宁省兴城市24-24第一学期11月阶段测试八年数学试卷pdf、24-25八上阶段测试二数学人教版答案1docx等2份试卷配套教学资源，其中试卷共16页， 欢迎下载使用。
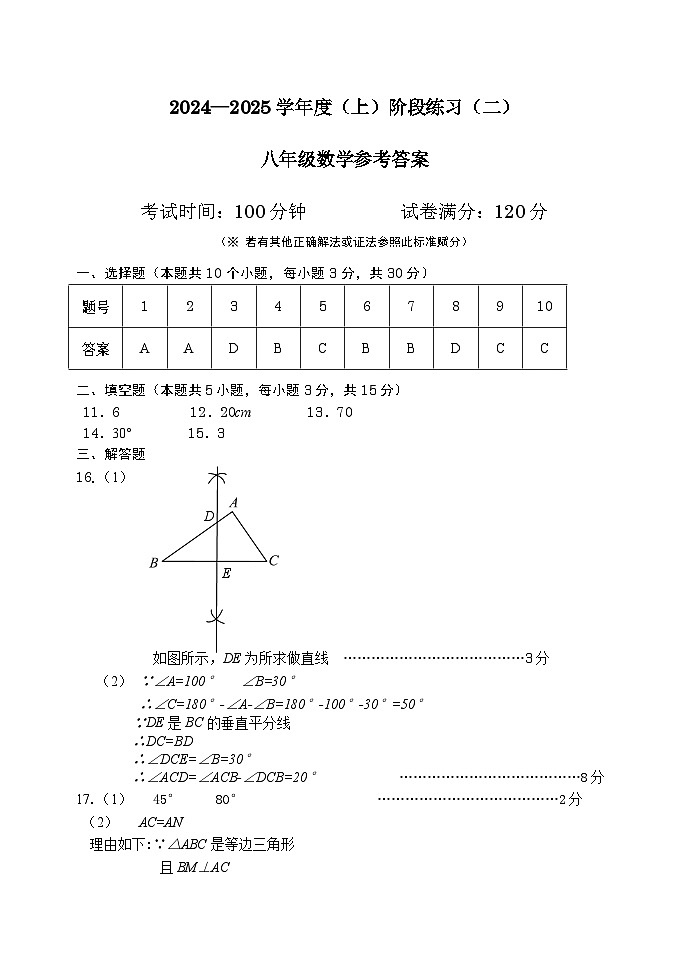
考试时间：100分钟 试卷满分：120分
（※ 若有其他正确解法或证法参照此标准赋分）
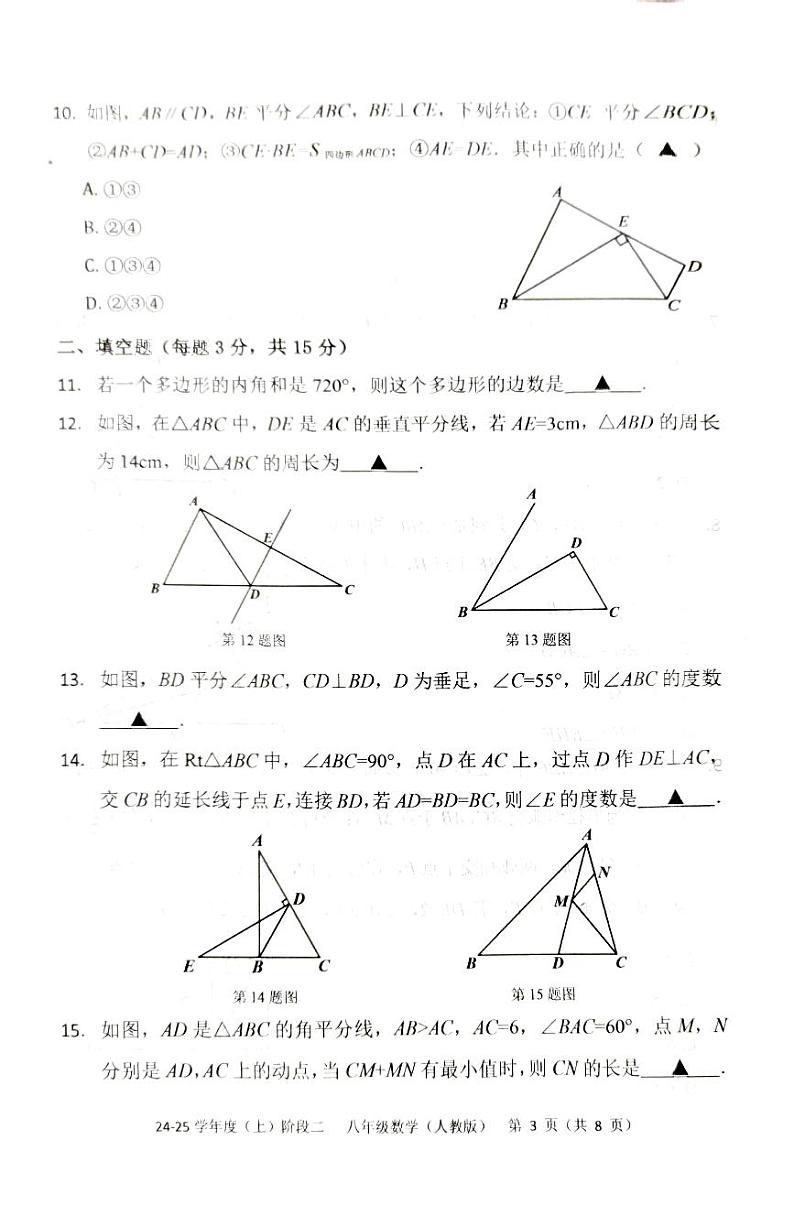
选择题（本题共10个小题，每小题3分，共30分）
二、填空题（本题共5小题，每小题3分，共15分）
11．6 12．20cm 13．70
14．30° 15．3
三、解答题
16．（1）
D
E

如图所示，DE为所求做直线 …………………………………3分
（2） ∵∠A=100° ∠B=30°
∴∠C=180°-∠A-∠B=180°-100°-30°=50°
∵DE是BC的垂直平分线
∴DC=BD
∴∠DCE=∠B=30°
∴∠ACD=∠ACB-∠DCB=20° …………………………………8分
17.（1） 45° 80° …………………………………2分
（2） AC=AN
理由如下:∵△ABC是等边三角形
且BM⊥AC
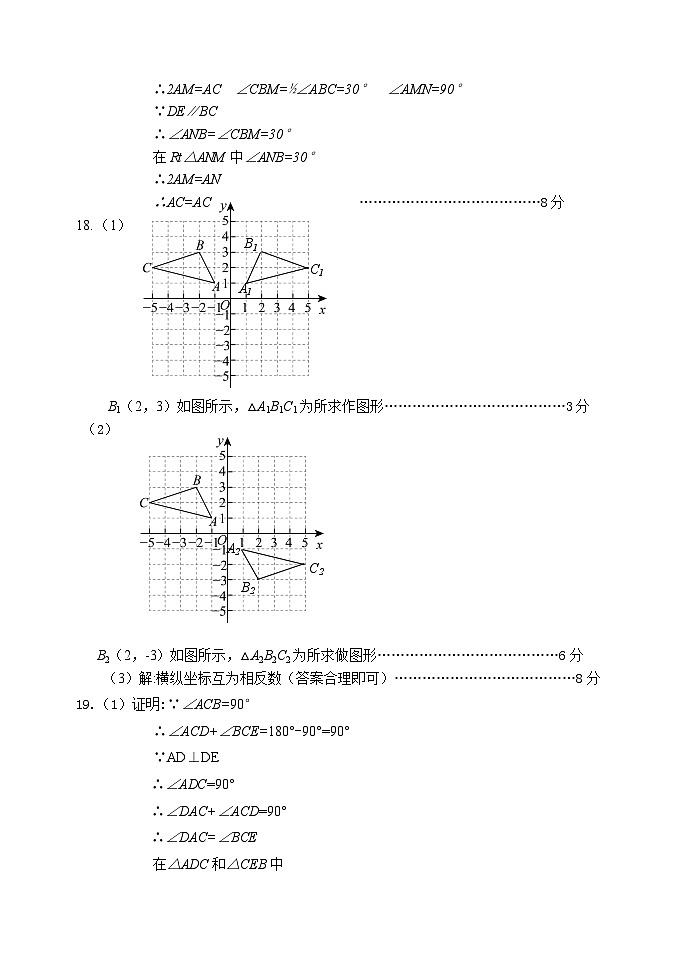
∴2AM=AC ∠CBM=½∠ABC=30° ∠AMN=90°
∵DE∥BC
∴∠ANB=∠CBM=30°
在Rt△ANM中∠ANB=30°
∴2AM=AN
∴AC=AC …………………………………8分
B1
（1）
C1
A1
B1（2，3）如图所示，△A1B1C1为所求作图形…………………………………3分
（2）
C2
A2
B2



B2（2，-3）如图所示，△A2B2C2为所求做图形…………………………………6分
（3）解:横纵坐标互为相反数（答案合理即可）…………………………………8分
19.（1）证明:∵∠ACB=90°
∴∠ACD+∠BCE=180°-90°=90°
∵AD⊥DE
∴∠ADC=90°
∴∠DAC+∠ACD=90°
∴∠DAC=∠BCE
在△ADC和△CEB中
∠DAC=∠BCE
∠ADC=∠CEB
AC=BC
∴△ADC≌△CEB（AAS） …………………………………4分
（2）∵△ADC≌△CEB
∴CE=AD=3×3=9，CD=BE=7×3=21
∴DE=CD+CE=21+9=30
答：两堵木墙之间的距离是30cm. …………………………………8分
20.解： ∵五边形ABCDE每个内角相等
∴∠ABC=∠AED=∠BAE=108° …………………………………2分
又∵EF平分∠AED
∴∠AEF=½∠AED=54° …………………………………4分
∵AB=BM
∴∠BAM=∠BMA= ½（180°-∠ABC） =36° …………………………6分
∴∠EFB=360°-∠AEF-∠EAB-∠B=360°-54°-108°-108°=90°
∴∠FNM=90°-∠M=90°-36°=54° …………………………9分 21.（1）证明:∵AB=AC且AD⊥BC
∴∠BAD=½∠BAC=60°
又∵AD=AB
∴△ABD是等边三角形 …………………………………4分
（2）由（1）知∠CAD=½∠BAC=60°
△ABD是等边三角形
∴∠ABD=60°=∠CAD
AD=BD
又∵∠ADB-∠ADE=∠EDF-∠ADE
∴∠BDE=∠ADF
在△BDE和△ADF中
BD=AD
∠BDE=∠ADF
∠ABD=∠CAD
∴△BDE≌△ADF（ASA）
∴BE=AF，DE=DF
∴AE+AF=AE+BE=AB
∴AE+DE+DF+AF=AB+DE+DF=16 …………………………………10分
（1）证明:延长CG交AB于点H
∵AC=BC，CG平分∠ACB
∴CH⊥AB，AH=BH
∴CH是AB的垂直平分线
即：点G在AB的垂直平分线上. …………………………………3分
(2) 补全图形 …………………………………5分
∵∠ACB=90°, AC=BC
∴∠CAB=∠CBA=45°
∵AD⊥AB
∴∠DAB=90°
∴∠DAC=∠DAB-∠CAB=90°-45°=45°
∴∠DAC=∠ACG
∵点E为AC中点
∴AE=CE
在△ADE和△CGE中
∠DAC=∠ACG
AE=CE
∠AED=∠CEG
∴△ADE≌△CGE（ASA）
∴AD=CG …………………………………8分
∵AD=AF
∴CG=AF
又∵CG平分∠ACB
∴∠BCG=∠ACG=½∠ACB=45°
∴∠BCG=∠CAB
在△BCG和△CAF中
CG=AF
∠BCG=∠CAB
BC=CA
∴△BCG≌△CAF（SAS）
∴∠CGB=∠AFC …………………………………11分
∵ ∠CFB+∠AFC=180°
∴∠CFB+∠CGB=180° ……………………………12分
23.（1）①选择丞丞同学
∵在BF上截取FQ=FC, 连接DQ
在△DFQ和△EFC中
QF=CF
∠QFD∠CFE
DF=EF
∴△DFQ≌△EFC（SAS）
∴∠DQF=∠ECF
∴CE∥DQ
∵CE∥AB
∴DQ∥AB
∴∠ABC=∠DQB
又∵BD∥AC
∴∠DBC=∠ACB
∵AB=AC
∴∠ABC=∠ACB
∴∠DBC=∠DQB
∵∠DQB+∠DQC=180°
∴∠DBC+∠BCE=180° …………………………………3分
②选择霖霖同学
过点E作EM∥AC交BC延长线于点M
∴∠M=∠ACB
∵BD∥AC
∴BD∥EM
∴∠M=∠ACB=∠DBC
∵AB∥CE
∴∠ABC=∠ECM
∵AB=AC
∴∠ABC=∠ACB
∴∠DBC=∠ECM
∵∠ECM+∠BCE=180°
∴∠DBC+∠BCE=180° 图（1）
图（2）
第25题图
图（1）
图（2）
第25题图
…………………………………3分
（2）过点D作DQ∥BE，交BC于Q点
∵DQ∥BE
∴∠QDE=∠DEA
∵点P是DE的中点
∴PD=PE
在△DPQ和△BPE中
∠QDE=∠DEA
PD=PE
∠DPQ=∠BPE
∴△DPQ≌△BPE（ASA）
∴DQ=BE
又∵DQ∥BE且△ABC为等边三角形
∴△CDQ为等边三角形
∴CQ=DQ=BE
又∵DM⊥CQ
∴CQ=2CM
即BE=2CM …………………………………7分
（3）过点A作AQ∥BD，交DM于点Q
∵AQ∥BD
∴∠QAB=∠ABD
∵点F是AB的中点
∴AF=BF
在△AFQ和△DFB中
∠AFQ=∠DFB
AF=BF
∠QAB=∠ABD
∴△AFQ≌△DFB
∴∠QAB=∠DBA
DB=AQ
∵△ABC是等腰直角三角形
∴AB=AC
∠ABC=∠CAB=45°
即∠CAQ+∠QAB=45°
又∵∠DBM=90°
∴∠DBA+∠CBM=45°
由上可知∠QAB=∠DBA
∴∠CAQ=∠CBM
∵△DBM为等腰直角三角形
∴DB=BM=AQ
在△ACQ和△BCM中
AC=BC
∠CAQ=∠CBM
AQ=BM
∴△ACQ≌△BCM
∴CM=CQ
∠ACQ=∠BCM
∵∠ACQ+∠QCB=90°
∴∠BCM+∠QCB=90°
即∠QCM=90°
∴△QCM为等腰直角三角形
∵S△ABC -S△DBM =8
∴S△CMQ =8
∴S△CMQ
∴CM=4 …………………………………12分 题号
1
2
3
4
5
6
7
8
9
10
答案
A
A
D
B
C
B
B
D
C
C