山东省聊城市茌平区2024-2025学年九年级上学期期中考试数学试题

这是一份山东省聊城市茌平区2024-2025学年九年级上学期期中考试数学试题，文件包含山东省聊城市茌平区2024-2025学年九年级上学期期中考试数学试题docx、期中考试九年级数学试题pdf、九年级期中卷数学答案docx、期中考试九年级数学答案卷pdf等4份试卷配套教学资源，其中试卷共17页， 欢迎下载使用。
填空
11.4m
12.36
13.1或7
14.66°
15.5或
16.
三．解答
17（8’）（1）计算：cs30°+tan45°﹣tan60°•cs245°．
【解答】解：原式＝+1﹣×（）2
＝+1+×
＝+1﹣
＝1．…………………………………………………………………………4’
(2)．计算：
【解答】解：原式＝
＝
＝
＝1．…………………………………………………………………………8’
18．（8’）如图，在平面直角坐标系中，△ABC的顶点坐标分别为A（﹣2，2），B（﹣4，0），C（﹣4，﹣4），在y轴右侧，以原点O为位似中心画一个△A'B'C'，使它与△ABC位似，且相似比是1：2．
（1）请画出△A'B'C'；
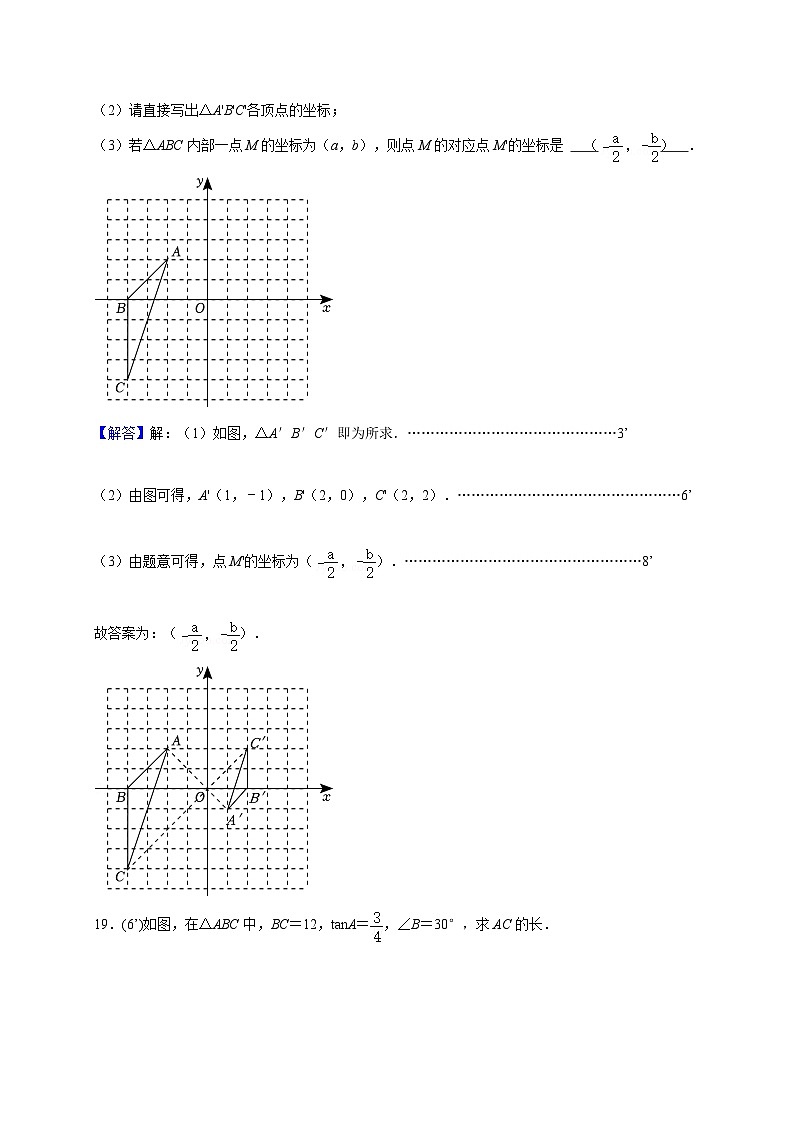
（2）请直接写出△A'B'C'各顶点的坐标；
（3）若△ABC内部一点M的坐标为（a，b），则点M的对应点M'的坐标是 （） ．
【解答】解：（1）如图，△A′B′C′即为所求．………………………………………3’
（2）由图可得，A'（1，﹣1），B'（2，0），C'（2，2）．…………………………………………6’
（3）由题意可得，点M'的坐标为（）．……………………………………………8’
故答案为：（）．
19．(6’)如图，在△ABC中，BC＝12，tanA＝，∠B＝30°，求AC的长．
【解答】1解：如图所示，过点C作CD⊥AB于D，
在Rt△DBC中，∠BDC＝90°，∠B＝30°，BC＝12，
∴，…………………………………………………2’
在Rt△ADC中，∠ADC＝90°，，
∴，
∴AD＝8，…………………………………………………4’
∴．…………………………………………………6’
20.(8’)如图，矩形ABCD中，E为BC上一点，DF⊥AE于F，若AB＝6，AD＝12，BE＝8，求DF的长．
【解答】解：∵DF⊥AE，
∴∠AFD＝90°．
∴∠B＝∠AFD＝90°．
又∵AD∥BC，
∴∠DAE＝∠AEB．
∴△ABE∽△DFA．…………………………………………………4’
∴，
∵AB＝6，BE＝8，∠B＝90°，
∴AE＝10．
∴．
∴DF＝7.2．…………………………………………………8’
21．(8’)在⊙O中，CD是直径，弦AB⊥CD，垂足为点E，连结AC，AD．
（1）求证：∠C＝∠BAD．
（2）若∠C＝30°，OC＝3，求AD的长度．
【解答】（1）证明：∵CD是直径，弦AB⊥CD，
∴，
∴∠C＝∠BAD；…………………………………………………4’
（2）解：如图，连接OA，
∵∠AOD＝2∠C＝2×30°＝60°，
∵OA＝OD，
∴△AOD等边三角形，
∴AD＝OC＝3．…………………………………………………8’
22(10’)．白云寺景区位于河南省新乡市辉县市西部三十公里的太行山下，寺内外共六棵千年银杏树，为唐代所植，树冠如盖，锦廷有上千平米，与古色古香的寺院相映成趣．千百年来这六棵银杏树，虽几经战火的劫难仍迥然纥立，默默守护着这座古守院，成为当地的一大景观和研究太行山植被的活化石．某校致学社团的同学们想要利用所学的知识测量某棵银杏树的高度，他们分成了三个小组并分别设计了不同的方案，测量方案与数据如下表：
（1）第 二 小组的数据无法算出银杏树的高度；
（2）请选择其中一个方案及其测量数据求出银杏树的高度．（结果精确到1m考考数据：sin37°＝0.60，cs37°≈0.80，tan37°≈0.75）
【解答】解：（1）由测量数据可知，第一组和第三组均可以计算出银杏树的高度，第二组仅给∠AGE＝37°，
∠BGE＝45°，还需要测量出一条边的数据，才可以计算出银杏树的高度；
故答案为：二．…………………………………………………3’
（2）①选择第一小组
由题意：∠B＝90°，∠ADB＝45°，
∴AB＝BD，…………………………………………………4’
设AB＝x米，
∵CD＝12m，
∴CB＝CD+BD＝（12+x）米，…………………………………6’
∵∠C＝37°，
∴，…………………………8’
∴x＝36，…………………………………………………10’
答：银杏树的高度约为36米；
②选择第三小组
由题意：∠B＝∠PFE＝90°，∠AFB＝45°，
∴AB＝BF，
∵EF＝9m，∠P＝37°，
∴，
∴PF＝12，
设AB＝x米，
∴BP＝PF+BF＝（12+x）米，
∴，
∴x＝36，
答：银杏树的高度约为36米．
23(12’)．如图，已知AB是⊙O的直径，点C，D在⊙O上，且BC＝CD．点E是线段AB延长线上一点，连接EC并延长交射线AD于点F．∠FEG的平分线EH交射线AC于点H，∠H＝45°．
（1）求证：EF是⊙O的切线；
（2）若BE＝2，CE＝4，求AF的长．
【解答】（1）证明：如图，连接OC，
∵OA＝OC，
∴∠OAC＝∠OCA，
∵BC＝CD，
∴弧BC=弧CD
∴∠DAC＝∠BAC，
∴∠OCA＝∠DAC，
∴OC∥AF，
∴∠OCE＝∠F…………………………………………………3’
∵EH平分∠FEG，
∴∠FEH＝∠GEH，
∵∠GEH＝∠H+∠BAC，∠FEH＝∠F+∠BAF，
∴2∠H+2∠BAC＝∠F+∠BAF，
∴∠BAF＝2∠BAC，
∴∠F＝2∠H＝90°，
∴∠OCE＝∠F＝90°，
即OC⊥EF，
∵OC是半径，
∴EF是⊙O的切线；…………………………………………………6’
解：设圆O半径为r，则OE=OB+BE=r+2
∵OC2+CE2=OE2
∴r2+42=(r+2)2
解得r=3
∴EA=AB+BE=8,OE=5…………………………………………………9’
∵AD∥OC
∴即
∴FA=…………………………………………………12’
24(12’)．如图，四边形ABCD和四边形AEFG都是正方形，C，F，G三点在一直线上，连接AF并延长交边CD于点M．
（1）求证：△MFC∽△MCA；
（2）求证△ACF∽△ABE；
（3）若DM＝1，CM＝2，求正方形AEFG的边长．
【解答】解：（1）∵四边形ABCD是正方形，四边形AEFG是正方形，
∴∠ACD＝∠AFG＝45°，
∵∠CFM＝∠AFG，
∴∠CFM＝∠ACM＝45°，
∵∠CMF＝∠AMC，
∴△MFC∽△MCA；………………………………………3’
（2）∵四边形ABCD是正方形，
∴∠ABC＝90°，∠BAC＝45°，
∴AC＝AB，
同理可得AF＝，
∴，
∵∠EAF＝∠BAC＝45°，
∴∠CAF+∠CAE＝∠BAE+∠CAE＝45°，
∴∠CAF＝∠BAE，
∴△ACF∽△ABE；………………………………………7’
（3）∵DM＝1，CM＝2，
∴AD＝CD＝1+2＝3，
∴AM＝，
∵△MFC∽△MCA，
∴，即，
∴FM＝，
∴AF＝AM﹣FM＝，
∴AF＝，
即正方形AEFG的边长为．………………………………………12’
声明：试题解析著作权属所有，未经书面同意，不得复制发布日期：2024/10/23 21:01:00；用户：初数30；邮箱：huide030@xyh.cm；学号：375370441
2
3
4
5
6
7
8
9
10
B
D
A
B
B
B
C
C
D
A
课题
测量银杏树AB的高度
测量工具
测量角度的仪器、皮尺等
测量小组
第一小组
第二小组
第三小组
测量方案示意图



说明
点C、D在点B的正西方向
GH是银杏树旁的房屋
EF是银杏树正西方向的指路牌，借助EF进行测量，使P、E、A三点在一条直线上，点P、F在点B的正西方向
测量数据
∠C＝37°，
∠ADB＝45°，
CD＝12m．
∠AGE＝37°，
∠BGE＝45°．
EF＝9m，∠P＝37°
∠AFB＝45°