2023-2024学年浙江省杭州市萧山区高桥初中教育集团八年级（上）调研数学试卷（12月份）

这是一份2023-2024学年浙江省杭州市萧山区高桥初中教育集团八年级（上）调研数学试卷（12月份），共8页。试卷主要包含了如果点A等内容，欢迎下载使用。
一．选择题（共10小题，30分）
1．已知三角形两条边的长分别为2、3，则第三条边的长可以是（ ）
A．1B．3C．5D．7
2．如果点A（a，2）在第二象限，那么a，b的取值范围是（ ）
A．a＞0B．a≥0C．a＜0D．a≤0
3．下列图形中，不一定是轴对称图形的是（ ）
A．线段B．角
C．直角三角形D．等腰三角形
4．若x＜y，则mx＞my成立的条件是（ ）
A．m＜0B．m≤0C．m＞0D．m≥0
5．能把一个任意三角形分成面积相等的两部分的是三角形的（ ）
A．角平分线B．中线C．高线D．边的中垂线
6．下列选项中，可以用来证明命题“若a2＞1，则a＞1”是假命题的反例是（ ）
A．a＝﹣2B．a＝﹣1C．a＝1D．a＝2
7．在一次函数y＝kx+b的图像上有两个点A（1，m），B（﹣2，n），则m与n的大小关（ ）
A．m＞nB．m＜nC．m＝nD．无法确定
8．如图，在△ABC中，AD是角平分线，AE是高，已知∠BAC＝2∠B，∠B＝4∠DAE，那么∠C的度数为（ ）
A．75°B．72°C．70°D．60°
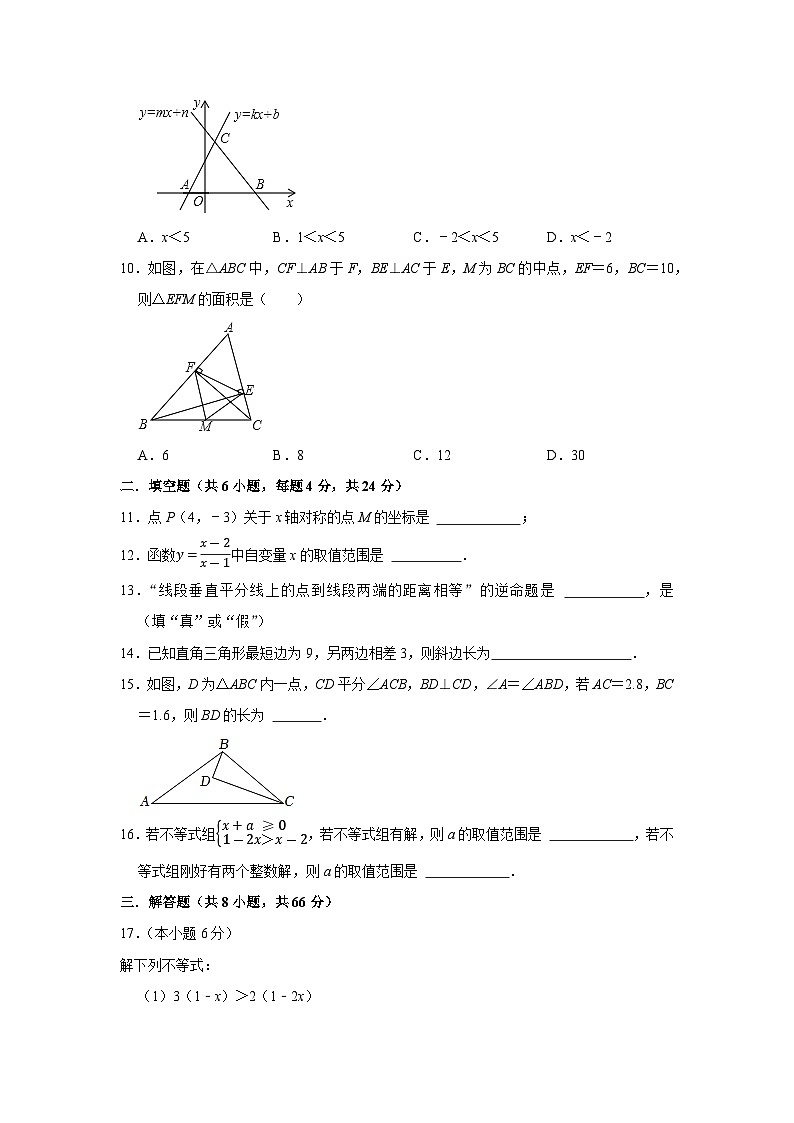
9．如图，直线y＝kx+b交x轴于点A（﹣2，0），直线y＝mx+n交x轴于点B（5，0），这两条直线相交于点C（2，c），则关于x的不等式组kx+b＜0mx+n＞0的解集为（ ）
A．x＜5B．1＜x＜5C．﹣2＜x＜5D．x＜﹣2
10．如图，在△ABC中，CF⊥AB于F，BE⊥AC于E，M为BC的中点，EF＝6，BC＝10，则△EFM的面积是（ ）
A．6B．8C．12D．30
二．填空题（共6小题，每题4分，共24分）
11．点P（4，﹣3）关于x轴对称的点M的坐标是 ；
12．函数y=x-2x-1中自变量x的取值范围是 ．
13．“线段垂直平分线上的点到线段两端的距离相等”的逆命题是 ，是 （填“真”或“假”）
14．已知直角三角形最短边为9，另两边相差3，则斜边长为 ．
15．如图，D为△ABC内一点，CD平分∠ACB，BD⊥CD，∠A＝∠ABD，若AC＝2.8，BC＝1.6，则BD的长为 ．
16．若不等式组x+a≥01-2x＞x-2，若不等式组有解，则a的取值范围是 ，若不等式组刚好有两个整数解，则a的取值范围是 ．
三．解答题（共8小题，共66分）
17．（本小题6分）
解下列不等式：
（1）3（1﹣x）＞2（1﹣2x）
（2）3-5x＞x-2(2x-1)3x-24＞2.5-x2．
18．（本小题6分）
已知：如图，∠1＝∠2，∠C＝∠E，AC＝AE，求证：△ABC≌△ADE．
19．（本小题6分）
如图，一次函数y＝kx+b的图象与过点A（1，4）和B（-2，-2）
（1）求函数解析式；
（2）其图像与x轴，y轴分别交于点C，点D，求线段CD的长
20．（本小题8分）
（1）请用直尺和圆规作∠B的角平分线交AC于点D，再过点D用尺规做BC的垂线角BC于E
（2）若∠A=90°，AB＝6，AC＝8，在（1）情况下，求CD的长．
21．（本小题8分）
已知一次函数y＝（m+1）x+3﹣m．
（1）若该函数时一次函数，则m应满足什么条件；
（2）在（1）的前提下，若其图像不经过第四象限，求m的取值范围；
（3）在（1）的前提下，若点A（a，b），B（a+1，c）在其图象上，求证：c-b-m=1
22．（本小题10分）
某校八年级举行迎亚运演讲比赛，购买A、B两种笔记本作为奖品，这两种笔记本的单价分别是12元和8元，他们准备购买这两种笔记本共30本，并且购买的A种笔记本的数量要少于B种笔记本数量的34，但又不少于B种笔记本数量的14．如果设他们买A种笔记本x本，买这两种笔记本共花费y元．
（1）请写出y（元）关于x（本）的函数关系式，并求出自变量x的取值范围；
（2）请问购买这两种笔记本各多少时花费最少？最少费用是多少元？
（3）商店为了促销，决定仅对A种类型的笔记本每本优惠a元销售（4＜a＜6），B种类型笔记本售价不变．请问此时购买这两种笔记本各多少时，花费最少？
23．（本小题10分）
如图，C为线段AE上一动点，（不与点A、E重合），在AE同侧分别作正△ABC和正△CDE，AD与BE交于点O，AD与BC交于点P，BE与CD交于点Q，连接PQ．
（1）求证：AD＝BE
（2）求证：△CQP是等边三角形
（3）若改变C的位置，其余条件都不变，点P恰好为BC的中点时，请问Q是否也为CD的中点，并说明理由．
24．（本小题12分）
已知直线l：y＝mx+n﹣1，有下列四个结论：
①当n＝5，m=-43时，原点到l的距离为3；
②当m＝﹣1时，直线l与直线l1：y＝2x+4的交点在第二象限，则n的范围为﹣1＜n＜5；
③当m＝n时，直线l经过定点（1，﹣1）；
④当m＝n＜0时，直线l与x轴交于点A，OA的长度始终大于1．
请你分别判断四个结论的真假，并给出理由．
参考答案与试题解析
一．选择题
二．填空题（共6小题）
三．解答题（共8小题）
17．解：（1）x＞﹣1，
（2）3-5x＞x-2(2x-1)①3x-24＞2.5-x2②，
由①得：x＜12；
由②得：x＞125，
则原不等式组无解．
18．证明：∵∠1＝∠2，
∴∠1+∠EAB＝∠2+∠EAB，
即∠CAB＝∠EAD，
在△ABC和△ADE中
∠C=∠EAC=AE∠CAB=∠EAD，
∴△ABC≌△ADE（ASA）．
19．解：（1）一次函数解析式为y＝2x+2；
（2）CD=5
20．（2）CD=254
21．解：（1）m≠﹣1
（2）3＞m＞-1
c-b=[(m+1)a+3-m]-[(m+1)(a+1)+3-m]
c-b=m+1
c-b-m=1
∴c-b-m=1
22．解：（1）依题意得：y＝12x+8（30﹣x）
即y＝4x+240
且x＜34（30﹣x）和x≥14（30﹣x）
解得6≤x＜907．
所以，y（元）关于x（本）的函数关系式为：y＝4x+240
自变量x的取值范围是6≤x＜907，x为整数；
（2）对于一次函数y＝4x+240
∵y随x的增大而增大，且6≤x＜907，x为整数，
故当x为6时，y的值最小，
此时，30﹣x＝30﹣6＝24，y＝4×6+240＝264（元）
因此，当买A种笔记本6本、B种笔记本24本时，所花费用最少，为264元；
（3）设他们买A种笔记本x本，B种笔记本（30﹣x）本，
则y＝（12﹣a）x+8（30﹣x），
∴y＝（4﹣a）x+240，
∴当a＜4时，x＝6，即买A种笔记本6本，B种笔记本24本，花费最少，
当a＝4时，6≤x＜，买A种笔记本6到12本，B种笔记本24到18本，花费＝240，
当a＞4时，x＝12，y最小，买A种笔记本12本，B种笔记本18本，花费最少．
23．证明：（1）∵△ABC和△CDE是正三角形，
∴AC＝BC，CD＝CE，∠ACB＝∠DCE＝60°，
∵∠ACD＝∠ACB+∠BCD，∠BCE＝∠DCE+∠BCD，
∴∠ACD＝∠BCE，
∴△ADC≌△BEC（SAS），
∴AD＝BE；
（2）∵ADC≌△BEC，
∴∠ACP＝∠BCQ，AC＝BC，∠CAP＝∠CBQ，
∴△APC≌△BQC（ASA）；
（3）∵P为BC中点
∴AP⊥BC
∴∠APC=90°=∠BQC
∴∠EQC=90°
∴Q为CD中点
24．解：①③错误，②④正确．理由如下：
①当n＝5，m=-43时，直线l对应的函数表达式为y=-43x+4．
令x＝0，得y＝4，令y＝0，得x＝3，
所以直线l与两坐标轴的交于点（3，0）和点（0，4），
所以直线l与两坐标轴交点围成的三角形的斜边长是32+42=5，
所以直线l到原点的距离为125，故①错误．
②当m＝﹣1时，直线l对应的函数表达式为y＝﹣x+n﹣1．
联立y=-x+n-1y=2x+4，得x=n-53y=2n+23．
因为直线l与直线l1的交点在第二象限，
所以x=n-53＜0y=2n+23＞0，
解得﹣1＜n＜5，故②正确．
③当m＝n时，直线l对应的函数表达式为y＝mx+m﹣1，
所以当x＝﹣1时，y＝﹣m+m﹣1＝﹣1，
所以直线l经过定点（﹣1，﹣1），故③错误．
④当m＝n＜0时，直线l经过第二、三、四象限，
所以直线l与x轴交于负半轴上的点A，
所以当y＝0时，0＝mx+n﹣1，解得x=1-nm．
当m＝n时，x=1m-1．
又因为m＜0，
所以1m-1＜0，即点A离原点的距离大于1，
所以OA的长度始终大于1，故④正确．
综上所述，①③错误，②④正确．
1
2
3
4
5
6
7
8
9
10
B
C
D
A
B
A
B
D
D
C
11
12
13
14
15
16
（4，3）
x≠1
到线段两端距离相等的点在这条线段的垂直平分线上
真
15
0.6
a＞-1
1≤a＜2