河南省濮阳市2024-2025学年八年级上学期11月期中考试数学试题

这是一份河南省濮阳市2024-2025学年八年级上学期11月期中考试数学试题，共12页。试卷主要包含了试题卷上不要答题，请用0，7米等内容，欢迎下载使用。

注意事项：
1.本卷分试题卷和答题卡两部分，试题卷共6页，三大题，满分120分，考试时间100 分钟；
2.试题卷上不要答题，请用0.5毫米黑色签字水笔直接把答案写在答题卡上，答在试题卷上的答案无效；
3.答题前，考生务必将本人所在学校、姓名、考场、座号、准考证号填写在答题卡第一面的指定位置上.
一、选择题 (每小题3分，共30分)
1.汉字是世界上最美的文字，形美如画、有的汉字是轴对称图形，下面四个汉字中是轴对称图形的是
2.如图，为了估计池塘两岸A，B间的距离，在池塘的一侧选取点P，测得PA=14 米，PB=9米，那么A ，B间的距离不可能是
A.6米
B.27米
C.8.7米
D.18米
3.若点A(a,3)与B(2,b)关于x轴对称,则点M(a,b)所在的象限是
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.如图的大桥是一座斜拉式大桥，斜拉式大桥多采用三角形结构，使其不易变形，这种做法的依据是
A.三角形的不稳定性
B.三角形的稳定性
C.四边形的不稳定性
D. 四边形的稳定性
八年级数学 第1页 (共6页) A 16° 11.54° C.48° D.72°
6.一副三角板按如图所示的位置叠放在一起，则图中∠α的度数是
A. 15°
B.10°
C. 5°
D.20°
7. 工人师傅常常利用角尺构造全等三角形的方法来平分一个角，如图，在∠AOB的两边OA、OB 上分别在取OC=OD，移动角尺，使角尺两边相同的刻度分别与点C、D重合，这时过角尺顶点 M的射线OM就是∠AOB的平分线，这里构造全等三角形的依据是
A. SSS
B. ASA
C. AAS
D. SAS
8.如图，如果△ABC≌△FED，那么下列结论错误的是
A. EC=BD
B. EF∥AB
C. DF=BD
D. AC∥FD
9.用一条宽相等的足够长的纸条，打一个结，如图1所示，然后轻轻拉紧、压平就可以得到如图2所示的正五边形ABCDE，则∠AFB的度数为
A.75° B.60° C.70° D.72°
10.如图,在△ABC中,AB=10,BC=8,AC=5,直线m是△ABC中AB边的垂直平分线,点P是直线m上的一动点，则△APC 周长的最小值为
A.10
B.13
C.18
D.15
八年级数学 第2页 (共6页)二、填空题(每小题3分，共15分)
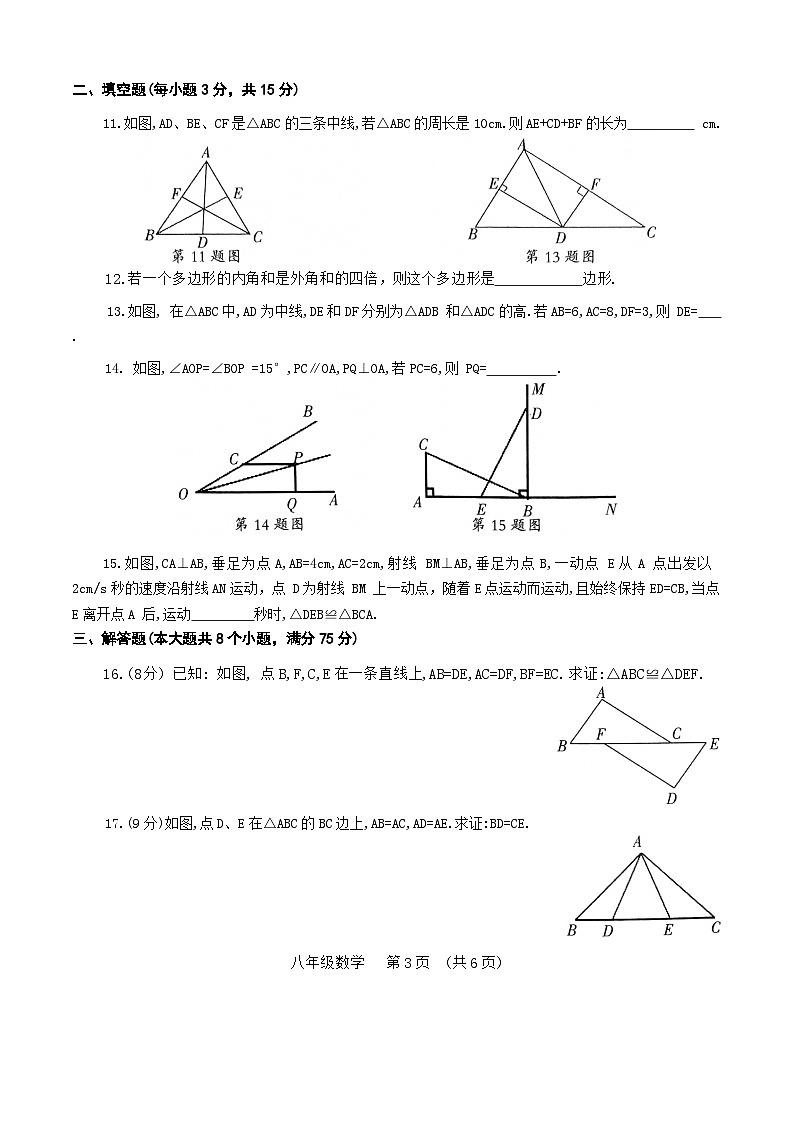
11.如图,AD、BE、CF是△ABC的三条中线,若△ABC的周长是10cm.则AE+CD+BF的长为 cm.
12.若一个多边形的内角和是外角和的四倍，则这个多边形是 边形.
13.如图, 在△ABC中,AD为中线,DE和DF分别为△ADB 和△ADC的高.若AB=6,AC=8,DF=3,则 DE= .
14. 如图,∠AOP=∠BOP =15°,PC∥OA,PQ⊥OA,若PC=6,则 PQ= .
15.如图,CA⊥AB,垂足为点A,AB=4cm,AC=2cm,射线 BM⊥AB,垂足为点B,一动点 E从A 点出发以 2cm/s秒的速度沿射线AN运动，点 D为射线 BM 上一动点，随着E点运动而运动,且始终保持ED=CB,当点E离开点A 后,运动 秒时,△DEB≌△BCA.
三、解答题(本大题共8个小题，满分75分)
16.(8分) 已知: 如图, 点B,F,C,E在一条直线上,AB=DE,AC=DF,BF=EC. 求证:△ABC≌△DEF.
17.(9分)如图,点D、E在△ABC的BC边上,AB=AC,AD=AE.求证:BD=CE.
八年级数学 第3页 (共6页)18.(9分) △ABC在平面直角坐标系中的位置如图所示.
(1)写出点A、B、C关于y轴的对称点. A₁、B₁、C₁的坐标；
(2)作出与 △ABC关于x轴对称的 △A₂B₂C₂ ;
(3)求出 △ABC的面积.
19.(9分) 如图，某游乐园有两个长度相等的滑梯BC与EF，滑梯BC的高AC与滑梯EF水平方向 DF的长度相等，∠DEF=30°. 国家安全部门针对滑梯类儿童游乐设备进行了安全范围内的考量，并作出了严格的安全界限：在滑行方向上，要求整体滑行区与水平面的夹角应不大于40°.请问滑梯BC与滑梯EF是否符合国家规定? 请说明理由.
(9分)如图,在 △ABC中,( CD⊥AB于点D,CE平分. ∠BCA交AB于点 E, ∠A=30°,
∠B=60°.
(1)求∠ACE的度数;
(2)求∠DCE 的度数.
八年级数学 第4页 (共6页)21.(10分)
(1)如图1,在△ABC中,已知点O是内角∠ABC、∠ACB的平分线的交点,若∠A=58°,求∠BOC的度数.
(2)如图2,在△ABC中,已知点O是外角∠CBE、∠BCF的平分线的交点,若∠A=α,求∠BOC 的度数(用含有α的式子表示).
22. (10分)阅读下面材料
【问题情境】
课外兴趣小组活动时，老师提出了如下问题：
如图①.在△ABC中,若AB=12,AC=8,求BC边上的中线AD取值范围.
小明在组内经过合作交流，得到了如下的解决方法：延长AD到点 E，使DE=AD，请根据小明方法思考：
(1)由已知和作图能得到△ADC≌△EDB的理由是 ;
A. HL B. SSS C. AAS D. SAS
(2)由三角形三边的关系可求得AD长的取值范围是 ；
解后反思：题中出现“中点”“中线”等条件，可考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集中到一个三角形中.
(3)【初步运用】
如图②,AD是△ABC的中线,BE交AC于E,交AD 于F,且AE=EF若EF=5,EC=3,求线段BF的长.
八年级数学 第5页 (共6页)23.(11分)如图,在 △ABC中， ∠C=90°,,AD平分 ∠CAB,DE⊥AB3于E,点F在边AC上,连接DF.
(1)求证: AC=AE;
(2)若 DF=DB,AB=5,AF=3,,求 BE 的长度;
(3)若 DF=DB,AB=m,AF=n,，直接写出BE的长度(用含 m，n的代数式表示)。
八年级数学 第6页 (共6页)
八年级数学期中考试
参考答案
一、选择题(每小题3分，共30分)
1.C 2.B 3.D 4.B 5.C 6.A 7.A 8.C 9.D 10.B
二．填空题(每小题3分，共15分)
11. 5 12.十 13.4 14.3 15. 1或3
三．解答题（共75分）
16.(8分) 证明：∵BF＝EC，
∴BF+FC＝EC+FC，即BC＝EF． ……………3分
在△ABC和△DEF中，
AB=DEAC=DFBC=EF， ……………6分
∴△ABC≌△DEF（SSS）． ……………8分
17. (9分)
证明：如图，过点A作AP⊥BC于P． ……………1分
∵AB＝AC，
∴BP＝CP； ……………3分
同理DP＝EP， ……………5分
∴BP﹣DP＝CP﹣EP， ……………7分
即BD＝CE.(方法不唯一，其它方法同样给分) ……………9分

18.（9分）解：（1）A1（2， 3），B1（3， 2），C1（1， 1）；
……………3分

（2）如图所示，△A2B2C2即为所求； ……………6分
（3）△ABC的面积为2×2-12×1×2-12×1×2-12×1×1=32．
……………9分
19.（9分） 解：在Rt△ABC和Rt△DEF中，
BC=EFAC=DF，
∴Rt△ABC≌Rt△DEF（HL）， ……………4分
∴∠DEF＝∠ABC＝30°， ……………6分
∴∠DFE＝90°﹣30°＝60°． ……………7分
∵∠ABC＜40°，∠DFE＞40°，
∴滑梯BC符合国家规定，滑梯EF不符合国家规定．
……………9分
20.（9分） 解：（1）在△ABC中，∠A＝30°，∠B＝60°，
∴∠ACB＝180°﹣∠A﹣∠B＝180°﹣30°﹣60°＝90°，
……………3分
∵CE是△ABC的角平分线，
∴∠ACE=12∠ACB＝12×90°＝45°； ……………5分
（2）∵CD⊥AB，
∴∠ADC＝90°， ……………7分
∴∠ACD＝90°﹣∠A＝90°﹣30°＝60°， ……………8分
∴∠DCE＝∠ACD﹣∠ACE
＝60°﹣45°＝15°． ……………9分
21．（10分）解：（1）∵∠ABC、∠ACB的平分线的交点，
∴∠OBC=12∠ABC，∠OCB=12∠ACB，
∴∠OBC+∠OCB=12（∠ABC+∠ACB）， ……………2分
∵∠A+∠ABC+∠ACB＝180°，∠A＝58°，
∴∠ABC+∠ACB＝180°﹣∠A＝122°，
∴∠OBC+∠OCB＝61°， ……………4分
∵∠BOC+∠OBC+∠OCB＝180°，
∴∠BOC＝180°﹣（∠OBC+∠OCB）＝180°﹣61°＝119°；
……………5分
（2）∵BO平分∠EBC，CO平分∠FCB，
∴∠OBC=12∠EBC，∠OCB=12∠FCB，
∵∠EBC＝180°﹣∠ABC，∠FCB＝180°﹣∠ACB，
∴∠OBC＝90°-12∠ABC，∠OCB＝90°-12∠ACB，
∴∠OBC+∠OCB＝180°-12（∠ABC+∠ACB）， ……………7分
∵∠A+∠ABC+∠ACB＝180°，∠A＝α°，
∴∠ABC+∠ACB＝180°﹣α，
∵∠OBC+∠OCB＝180°-12（180°﹣α）＝90°+12α．
……………9分
∵∠BOC+∠OBC+∠OCB＝180°，
∴∠BOC＝180°﹣（∠OBC+∠OCB）＝180°﹣（90°+12α）＝90°-12α．
……………10分
22．（10分）
解：（1）D ……………2分
（2）2＜AD＜10； ……………4分
（3）解：延长AD到G，使DG＝AD，连接BG，……………5分
由（1）知△ADC≌△GDB，
∴∠G＝∠DAC，
BG＝AC， ……………6分
∵AE=EF=5,CE=3,
∴AC=AE+CE=8,
∴BG＝8, ……………7分
∵AE＝EF，
∴∠DAC＝∠AFE， ……………8分
∵∠G＝∠DAC，
∴∠G＝∠AFE，
又∵∠BFG＝∠AFE，
∴∠G＝∠BFG， ……………9分
∴BF＝BG＝8． ……………10分
23．（11分）（1）证明：∵∠C＝90°，
∴DC⊥AC，
又∵DE⊥AB，AD平分∠CAB，
∴DC＝DE. …………2分

在Rt△ACD和Rt△AED中，
∵AD=ADDC=DE ，
∴Rt△ACD≌Rt△AED（HL）， …………4分
∴AC＝AE； …………5分
（2）解：
在Rt△CDF和Rt△EDB中，
∵DF=DBDC=DE ，
∴Rt△CDF≌Rt△EDB（HL），
∴CF＝BE， …………7分
∵AB＝AE+BE，AE＝AC，
∴AB＝AC+BE＝AF+CF+BE＝AF +2BE，
∵AB＝5，AF＝3，
∴BE=12(AB - AF)=12×(5-3)=1 …………9分
（3）BE= 12 (m-n) …………11分