2025年中考数学一轮复习题型分类练习专题28 菱形的性质与判定【十四大题型】（2份，原卷版+解析版）

这是一份2025年中考数学一轮复习题型分类练习专题28 菱形的性质与判定【十四大题型】（2份，原卷版+解析版），文件包含2025年中考数学一轮复习题型分类练习专题28菱形的性质与判定十四大题型原卷版docx、2025年中考数学一轮复习题型分类练习专题28菱形的性质与判定十四大题型解析版docx等2份试卷配套教学资源，其中试卷共121页， 欢迎下载使用。
TOC \ "1-3" \h \u
\l "_Tc1078" 【题型1 根据菱形的性质求周长、角度、线段长、面积、坐标】 PAGEREF _Tc1078 \h 2
\l "_Tc14507" 【题型2 菱形的判定定理的理解】 PAGEREF _Tc14507 \h 3
\l "_Tc15708" 【题型3 证明四边形是菱形】 PAGEREF _Tc15708 \h 4
\l "_Tc21065" 【题型4 根据菱形的性质与判定求线段长】 PAGEREF _Tc21065 \h 5
\l "_Tc20216" 【题型5 根据菱形的性质与判定求角度】 PAGEREF _Tc20216 \h 6
\l "_Tc31036" 【题型6 根据菱形的性质与判定求面积】 PAGEREF _Tc31036 \h 8
\l "_Tc24940" 【题型7 根据菱形的性质与判定解决多结论问题】 PAGEREF _Tc24940 \h 9
\l "_Tc23575" 【题型8 与菱形有关的新定义问题】 PAGEREF _Tc23575 \h 10
\l "_Tc22996" 【题型9 与菱形有关的规律探究问题】 PAGEREF _Tc22996 \h 13
\l "_Tc16656" 【题型10 与菱形有关的动点问题】 PAGEREF _Tc16656 \h 14
\l "_Tc11503" 【题型11 菱形与一次函数综合】 PAGEREF _Tc11503 \h 16
\l "_Tc31686" 【题型12 菱形与反比例函数综合】 PAGEREF _Tc31686 \h 17
\l "_Tc12886" 【题型13 菱形与一次函数、反比例函数综合】 PAGEREF _Tc12886 \h 18
\l "_Tc22042" 【题型14 菱形与二次函数综合】 PAGEREF _Tc22042 \h 20
【知识点 菱形的性质与判定】
菱形的定义：有一组邻边相等的平行四边形叫做菱形.
菱形的性质：
1）具有平行四边形的所有性质；
2）四条边都相等；
3）两条对角线互相垂直，且每条对角线平分一组对角.
4）菱形既是中心对称图形，又是轴对称图形，菱形的对称中心是菱形对角线的交点，菱形的对称轴是菱形对角线所在的直线，菱形的对称轴过菱形的对称中心.
菱形的判定：
1）A
对角线互相垂直的平行四边形是菱形.
2）一组邻边相等的平行四边形是菱形.
3）四条边相等的四边形是菱形.
【解题思路】判定一个四边形是菱形时，可先说明它是平行四边形，再说明它的一组邻边相等或它的对角线互相垂直，也可直接说明它的四条边都相等或它的对角线互相垂直平分．
菱形的面积公式：S=ah=对角线乘积的一半（其中a为边长，h为高）.
菱形的周长公式：周长l=4a（其中a为边长）.
【题型1 根据菱形的性质求周长、角度、线段长、面积、坐标】
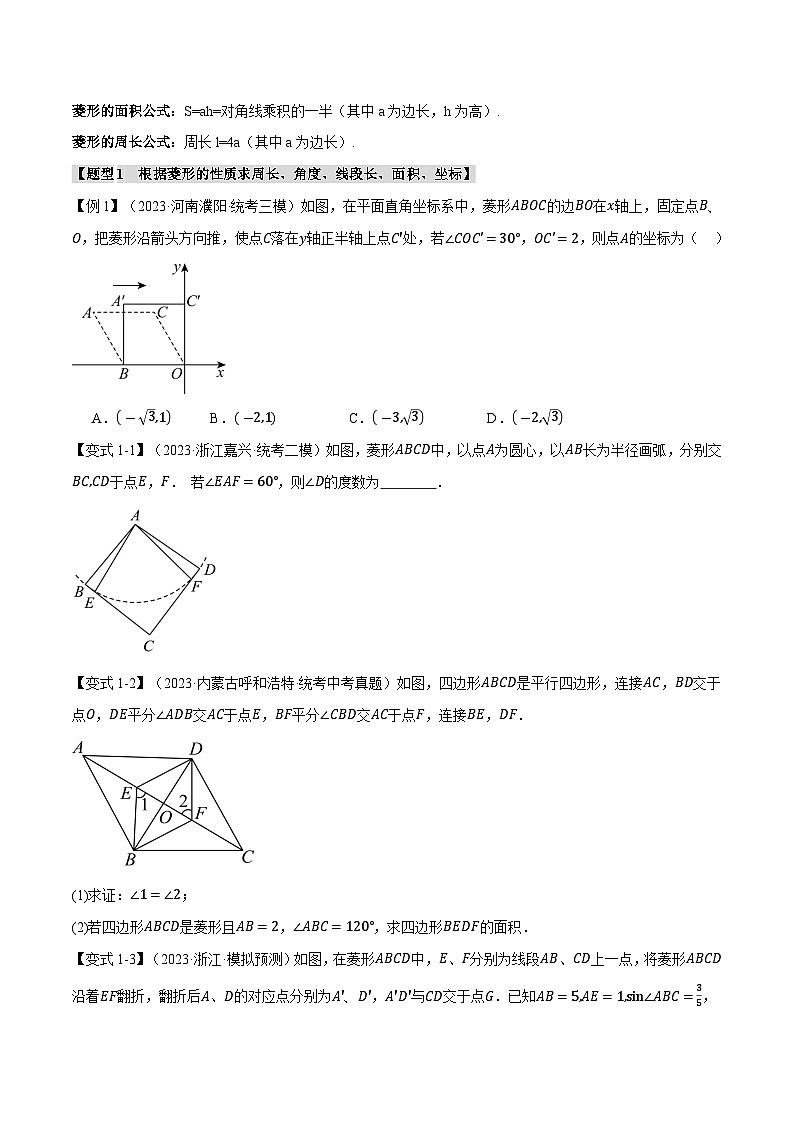
【例1】（2023·河南濮阳·统考三模）如图，在平面直角坐标系中，菱形ABOC的边BO在x轴上，固定点B、O，把菱形沿箭头方向推，使点C落在y轴正半轴上点C'处，若∠COC'=30°，OC'=2，则点A的坐标为（ ）

A．-3,1B．-2,1C．-3,3D．-2,3
【变式1-1】（2023·浙江嘉兴·统考二模）如图，菱形ABCD中，以点A为圆心，以AB长为半径画弧，分别交BC,CD于点E，F． 若∠EAF=60°，则∠D的度数为 ．

【变式1-2】（2023·内蒙古呼和浩特·统考中考真题）如图，四边形ABCD是平行四边形，连接AC，BD交于点O，DE平分∠ADB交AC于点E，BF平分∠CBD交AC于点F，连接BE，DF．
(1)求证：∠1=∠2；
(2)若四边形ABCD是菱形且AB=2，∠ABC=120°，求四边形BEDF的面积．
【变式1-3】（2023·浙江·模拟预测）如图，在菱形ABCD中，E、F分别为线段AB、CD上一点，将菱形ABCD沿着EF翻折，翻折后A、D的对应点分别为A'、D'，A'D'与CD交于点G．已知AB=5,AE=1,sin∠ABC=35，若EF∥AD,A'G= 若∠EFD=135°,A'G= ．

【题型2 菱形的判定定理的理解】
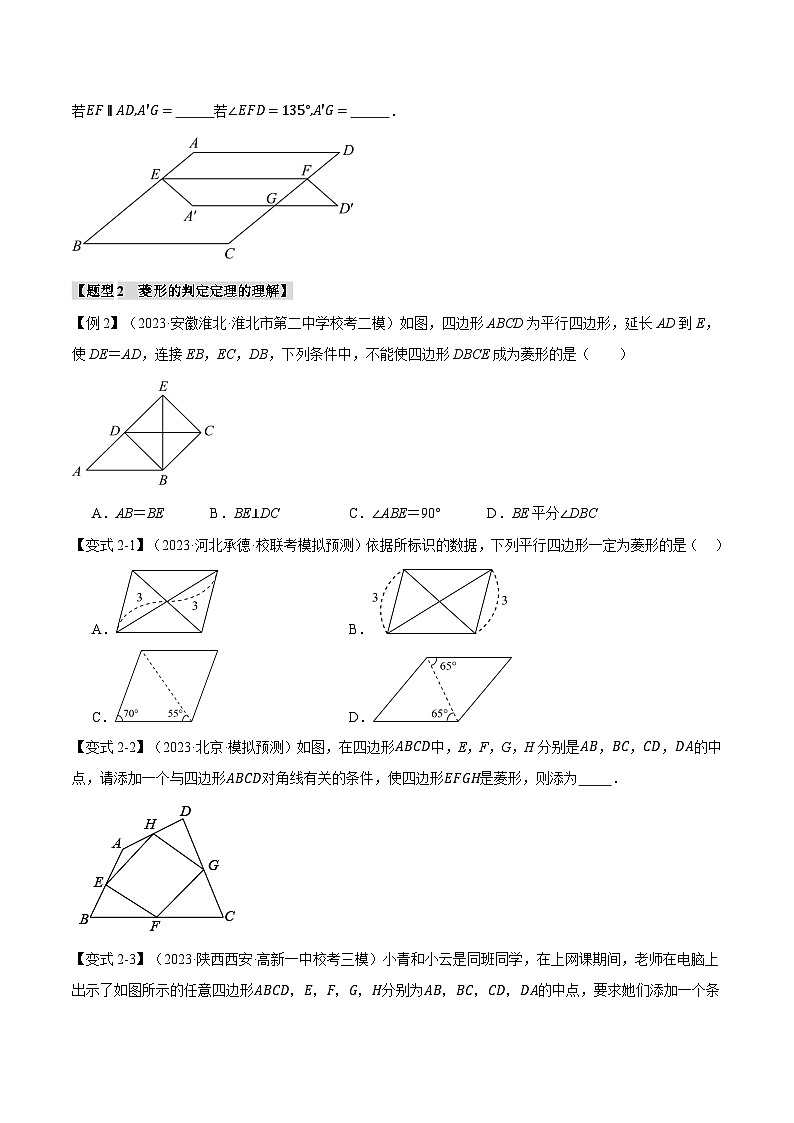
【例2】（2023·安徽淮北·淮北市第二中学校考二模）如图，四边形ABCD为平行四边形，延长AD到E，使DE＝AD，连接EB，EC，DB，下列条件中，不能使四边形DBCE成为菱形的是（ ）
A．AB＝BEB．BE⊥DCC．∠ABE＝90°D．BE平分∠DBC
【变式2-1】（2023·河北承德·校联考模拟预测）依据所标识的数据，下列平行四边形一定为菱形的是（ ）
A． B．
C． D．
【变式2-2】（2023·北京·模拟预测）如图，在四边形ABCD中，E，F，G，H分别是AB，BC，CD，DA的中点，请添加一个与四边形ABCD对角线有关的条件，使四边形EFGH是菱形，则添为 ．
【变式2-3】（2023·陕西西安·高新一中校考三模）小青和小云是同班同学，在上网课期间，老师在电脑上出示了如图所示的任意四边形ABCD，E，F，G，H分别为AB，BC，CD，DA的中点，要求她们添加一个条件使得四边形EFGH为菱形，小青添加的条件是AC=BD，小云添加的条件是EG⊥HF，则下列说法正确的是（ ）
A．小青和小云都正确B．小青正确，小云错误
C．小青错误，小云正确D．小青和小云都错误
【题型3 证明四边形是菱形】
【例3】（2023·湖南岳阳·统考二模）已知：如图，在▱ABCD中，点E，F分别在AD，BC上，BE平分∠ABC．请从以下三个条件：①AE=BF；②AB=EF；③AB∥EF中，选择一个合适的条件，使四边形ABFE为菱形．

(1)你添加的条件是_______（填序号）；
(2)添加了条件后，请证明四边形ABFE为菱形．
【变式3-1】（2023·陕西西安·校考二模）如图，AB∥CD，连接BC，请用尺规作图法，分别在AB，CD上求作E，F，连接CE，BF，使得四边形CEBF是菱形．（保留作图痕迹，不写作法）
【变式3-2】（2023·浙江杭州·校考二模）已知：如图，在平行四边形ABCD中，∠ABC 的平分线交AD于点E，点F是BE的中点，连接AF并延长交BC于点G，连接EG，CF．

(1)求证：四边形AEGB是菱形；
(2)若tan∠ABC=3，CD=8，AD=10，求CF的长．
【变式3-3】（2023·江西吉安·校考三模）如图，在△ABC中，AB=BC=4，∠C=30°，D是BC上的动点，以D为圆心，DC的长为半径作圆交AC于点E，F，G分别是AB，AE上的点，将△AFG沿FG折叠，点A与点E恰好重合．

(1)如图1，若CD=83-12，证明⊙D与直线AB相切；
(2)如图2，若⊙D经过点B，连接ED．
①BE的长是 ；
②判断四边形BFED的形状，并证明．
【题型4 根据菱形的性质与判定求线段长】
【例4】（2023·浙江温州·校联考模拟预测）如图，在Rt△ABC中，∠ACB=90°，AE平分∠CAB交CB于点E，CD⊥AB于点D，交AE于点G，过点G作GF∥BC交AB于F，连接EF．
(1)求证：CG=CE；
(2)若AC=3cm，BC=4cm，求线段DG的长度．
【变式4-1】（2023·甘肃兰州·统考中考真题）如图，矩形ABCD的对角线AC与BD相交于点O，CD∥OE，直线CE是线段OD的垂直平分线，CE分别交OD，AD于点F，G，连接DE．

(1)判断四边形OCDE的形状，并说明理由；
(2)当CD=4时，求EG的长．
【变式4-2】（2023·陕西西安·校考二模）如图，在菱形ABCD中，∠ABC=60°，AD=6，对角线AC、BD相交于点O，点E在线段AC上，且AE=2，点F为线段BD上的一个动点，则EF+ 12 BF的最小值为 ．
【变式4-3】（2023·广东惠州·统考二模）如图，把矩形ABCD沿AC折叠，使点D与点E重合，AE交BC于点F，过点E作EG∥CD交AC于点G，交CF于点H，连接DG．

(1)试判断四边形ECDG的形状，并加以证明；
(2)连接ED交AC于点O，求证：DC2=OC⋅AC；
(3)在（2）的条件下，若DG=6，AG=145，求CG的值．
【题型5 根据菱形的性质与判定求角度】
【例5】（2023·江苏泰州·统考二模）如图1，将Rt△ABC∠A=90°纸片按照下列图示方式折叠：①将△ABD沿BD折叠，使得点A落在BC边上的点M处，折痕为BD；②将△BEF沿EF折叠，使得点B与点D重合，折痕为EF；③将△DEF沿DF折叠，点E落在点E'处，展开后如图2，BD、PF、DF、DP为图1折叠过程中产生的折痕．
(1)求证：DP∥BC；
(2)若DE'落在DM的右侧，求∠C的范围；
(3)是否存在∠C使得DE与∠MDC的角平分线重合，如存在，请求∠C的大小；若不存在，请说明理由．
【变式5-1】（2023·湖北襄阳·校考一模）如图，▱ABCD中，AB=AD，点E是AB上一点，连接CE、DE，且BC=CE，若∠BCE=40°，则∠ADE= ．
【变式5-2】（2023·黑龙江哈尔滨·统考中考真题）已知四边形ABCD是平行四边形，点E在对角线BD上，点F在边BC上，连接AE，EF，DE=BF，BE=BC．

(1)如图①，求证△AED≌△EFB；
(2)如图②，若AB=AD，AE≠ED，过点C作CH∥AE交BE于点H，在不添加任何轴助线的情况下，请直接写出图②中四个角（∠BAE除外），使写出的每个角都与∠BAE相等．
【变式5-3】（2023·安徽合肥·统考三模）如图，在四边形ABCD中，∠ABC=120°，对角线BD平分∠ABC，BD=BC，E为BD上一点，且BA=BE，连接AC交BD于点F，G为BC上一点，满足BF=BG，连接EG交AC于点H，连接BH．

(1)①求证：∠EHF=60°；
②若H为EG中点，求证：AF2=2EF⋅EB；
(2)若AC平分∠DAB，请直接写出∠ECA与∠ACB的关系：________________．
【题型6 根据菱形的性质与判定求面积】
【例6】（2023·贵州遵义·统考一模）小明学习菱形时，对矩形ABCD进行了画图探究AD>AB，其作法和图形如下：
①连接BD；
②分别以点B，D为圆心，大于BD长的一半为半径作弧，两弧相交于M，N两点，作直线MN交BD于点O，交AD于点E，交BC于点F；
③连接BE，DF．
(1)根据以上作法，判断四边形BFDE的形状，并说明理由；
(2)若AB=4，AD=8，求四边形BFDE的面积．
【变式6-1】（2023下·内蒙古包头·九年级统考期末）如图，某同学剪了两条宽均为3的纸条，交叉叠放在一起，且它们的交角为60°，则它们重叠部分的面积为（ ）．
A．3B．23C．36D．6
【变式6-2】（2023·广西玉林·统考模拟预测）在矩形ABCD中，两条对角线AC,BD相交于点O，C作AM∥BD,CN∥BD，且AM=CN=BD，连接MN．
(1)判断四边形AMNC的形状，并说明理由；
(2)若AB=6,∠ACB=30°，求四边形AMNC的面积．
【变式6-3】（2023下·广东珠海·八年级校考期中）已知：如图，AD是△ABC的角平分线，DE∥AC交AB于点E，DF∥AB交AC于点F．

(1)求证：四边形AEDF是菱形；
(2)若AE=13，AD=24，试求四边形AEDF的面积．
【题型7 根据菱形的性质与判定解决多结论问题】
【例7】（2023·山东青岛·模拟预测）如图，菱形ABCD中，∠BAD=60°，AC与BD交于点O，E为CD延长线上一点，且CD=DE，连结BE，分别交AC，AD于点F，G，连结OG， ①OG=12AB②S四边形ODGF=S△ABF③由点A、B、D、E构成的四边形是菱形；④S△ACD=2S△ABG中正确的结论是（ ）
A．①③B．②④C．①②③D．①②③④
【变式7-1】（2023·山东青岛·山东省青岛第二十六中学校考二模）如图，将矩形ABCD沿AE折叠，点D的对应点落在BC上点F处，过点F作FG∥CD，连接EF，DG，下列结论中正确的有( )
①∠ADG=∠AFG；②四边形DEFG是菱形；③DG2=12AE•EG；④若AB=4，AD=5，则CE=1．
A．①②③④B．①②③C．①③④D．①②
【变式7-2】（2023·黑龙江佳木斯·统考三模）如图，在Rt△ABC中，AB=CB，BE⊥AC，∠BAC的平分线AD交BE于点G，BO⊥AD于点O，交AC于点F，连接GF，DF．下列结论：①tan∠BAD=12；②四边形BDFG是菱形；③CE=(2+1)GE；④S四边形GDFE=S△AEG．上述结论中正确的序号是（ ）

A．①②③B．②③④C．①②④D．①②③④
【变式7-3】（2023·山东泰安·统考二模）如图，正△ABC的边长为2，沿△ABC的边AC翻折得△ADC，连接BD交AC于点O，点M为BC上一动点，连接AM，射线AM绕点A逆时针旋转60°交BC于点N，连接MN、OM．以下四个结论：①△AMN是等边三角形：②MN的最小值是3；③当MN最小时S△CMN=18S菱形ABCD；④当OM⊥BC时，OA2=DN⋅AB．正确的是（ ）

A．①②③B．①②④C．①③④D．①②③④
【题型8 与菱形有关的新定义问题】
【例8】（2023下·安徽六安·二模）阅读短文，解决问题
定义：三角形的一个角与菱形的一个角重合，且菱形的这个角的对角顶点在三角形的这个角的对边上，则称这个菱形为该三角形的“亲密菱形”．例如：如图1，四边形AEFD为菱形，∠BAC与∠DAE重合，点F在BC上，则称菱形AEFD为△ABC的“亲密菱形”．
如图2，在Rt△ABC中，∠B＝90°，AF平分∠BAC，交BC于点F，过点F作FD∥AC，EF∥AB．
(1)求证：四边形AEFD为△ABC的“亲密菱形”；
(2)若AC＝12，FC＝26，求四边形AEFD的周长；
(3)如图3，M、N分别是DF、AC的中点，连接MN．若MN＝3，求AD2＋CF2的值．
【变式8-1】（2023·广西崇左·统考二模）筝形的定义：两组邻边分别相等的四边形叫做筝形．
(1)根据筝形的定义，写出一种学过的满足筝形的定义的四边形：______；
(2)如图1，在正方形ABCD中，E是对角线BD延长线上一点，连接AE，CE．求证：四边形ABCE是筝形：
(3)小明学习筝形后对筝形非常感兴趣，购买了一只风筝，通过测量它的主体（如图2）得AB=AD，BC=DC，发现它是一个筝形，还得到AB=18cm，BC=40cm，∠ABC=120°，求筝形ABCD的面积．
【变式8-2】（2023·陕西渭南·统考二模）【定义新知】
定义：有两个相邻内角互余的四边形称为邻余四边形，这两个角的夹边称为邻余线．
(1)如图1，在5×4的方格中，点A、B在格点上，请画出一个符合条件的邻余四边形ABEF，使得AB是邻余线，点E、F在格点上；
【问题研究】
(2)如图2，已知四边形ABCD是以AB为邻余线的邻余四边形，AB=20，AD=8，BC=4，∠ADC=135°，求CD的长；
【问题解决】
(3)如图3是某公园的一部分，四边形ABCD是平行四边形，对角线AC、BD交于点O，点E在OC上，△BOC是一个人工湖，OQ是湖上的一座桥，现公园规划人员要在桥上修建一个湖心亭M，若EM的延长线与OB的交点为F，按规划要求M是EF的中点．已知BC=200米，AC=240米，CQ=60米，OE=2EC，且四边形BCEF始终是以BC为邻余线的邻余四边形．规划人员经过思考后，在图纸上找出AB的中点N，连接EN，与OB、OQ的交点分别是点F和点M的位置．请问，按照规划人员的方法修建的湖心亭M是否符合规划的要求？请说明理由．
【变式8-3】（2023·江苏盐城·统考一模）定义：若四边形中某个顶点与其它三个顶点距离相等，则这个四边形叫做等距四边形，这个顶点叫做这个四边形的等距点．

(1)判断：一个内角为60°的菱形________等距四边形．（填“是”或“不是”）
(2)如图2，在5×5的网格图中有A、B两点，请在答题卷给出的两个网格图上各找出C、D两个格点，使得以A、B、C、D为顶点的四边形以A为等距点的“等距四边形”，画出相应的“等距四边形”（互不全等），并写出该等距四边形的端点均为非等距点的对角线长．端点均为非等距点的对角线长为________．
(3)如图，在海上A，B两处执行任务的两艘巡逻艇，根据接到指令A，B两艇同时出发，A艇直接回到驻地O，B艇到C岛执行某项任务后回到驻地O（在C岛执行任务的时间忽略不计），已知A，B，C三点到O点的距离相等，AO∥BC，BC=100km，tanA=32，若A艇速度为65km/h，试问B艇的速度是多少时，才可以和A艇同时回到驻地？
【题型9 与菱形有关的规律探究问题】
【例9】（2023·贵州铜仁·校考一模）如图，菱形ABCD中，∠ABC=120°，AB=1，延长CD至A1，使DA1=CD，以A1C为一边，在BC的延长线上作菱形A1CC1D1，连接AA1，得到△ADA1；再延长C1D1至A2，使D1A2=C1D1，以A2C1为一边，在CC1的延长线上作菱形A2C1C2D2，连接A1A2，得到△A1D1A2…按此规律，得到△A2021D2021A2022，记△ADA1的面积为S1，△A1D1A2的面积为S2⋅⋅⋅，△A2021D2021A2022的面积为S2022，则S2022= ．

【变式9-1】（2023·山东泰安·校考模拟预测）如图，ΔABC是边长为1的等边三角形，分别取AC，BC边的中点D，E，连接DE，作EF∥AC得到四边形EDAF，它的周长记作C1；分别取EF，BE的中点D1，E1连接D1E1，作E1F1∥EF，得到四边形E1D1FF1，它的周长记作C2，照此规律作下去，则C2021等于 ．
【变式9-2】（2023·四川广安·模拟预测）如图，在菱形ABCD中，边长为1，∠A=60°，顺次连接菱形ABCD各边中点，可得四边形A1B1C1D1；顺次连接四边形A1B1C1D1各边中点，可得四边形A2B2C2D2；顺次连接四边形A2B2C2D2各边中点，可得四边形A3B3C3D3；按此规律继续下去，…，则四边形A2023B2023C2023D2023的面积是 ．
【变式9-3】（2023·黑龙江绥化·三模）如图，边长为1的菱形ABCD中，∠DAB=60°．连接对角线AC，以AC为边作第二个菱形ACEF，使∠FAC=60°．连接AE，再以AE为边作第三个菱形AEGH使∠HAE=60°…按此规律所作的第n个菱形的边长是 ．

【题型10 与菱形有关的动点问题】
【例10】（2023·河南周口·校考三模）如图，在菱形OABC中，∠BCO=60°，点C-3,0，点D在对角线BO上，且OD=2BD，点E是射线AO上一动点，连接DE,F为x轴上一点（F在DE左侧)，且∠EDF=60°，连接EF，当△DEF的周长最小时，点E的坐标为（ ）

A．1,3B．-1,-3C．12,32D．0,0
【变式10-1】（2023·福建泉州·校联考模拟预测）如图，已知AB=8，P为线段AB上的一个动点，分别以AP，PB为边在AB的同侧作菱形APCD和菱形PBFE，点P，C，E在一条直线上，∠DAP=60°．M，N分别是对角线AC，BE的中点．当点P在线段AB上移动时，点M，N之间的距离最短为 ．

【变式10-2】（2023·陕西咸阳·校考三模）如图，在菱形ABCD中，对角线AC、BD相交于点O，点E、F分别是OD、OC上的两个动点，且EF=4，P是EF的中点，连接OP、PC、PD，若AC=12,BD=16，则PC+14PD的最小值为 ．

【变式10-3】（2023·江苏淮安·统考三模）如图，已知菱形ABCD中，∠ABC=120°，AB=4，点E为CD边上一动点(不含端点)，射线AE交∠BCD外角平分线于点F，连接AC、BF，BF交AC于点H，交DC于点G．

(1)求出∠ACF的度数；
(2)当CF=2时，求BF的长；
(3)当E是CD中点时，试说明EF=14AF；
(4)在点E运动过程中，CGGE的值是否发生改变？请说明理由．
【题型11 菱形与一次函数综合】
【例11】（2023·江苏盐城·校考三模）如图，菱形ABCD的顶点A(1,0)、B(7,0)在x轴上，∠DAB=60°，点E在边BC上且横坐标为8，点F为边CD上一动点，y轴上有一点P(0,-533)．当点P到EF所在直线的距离取得最大值时，点F的坐标为 ．

【变式11-1】（2023·山东青岛·统考三模）如图，在平面直角坐标系中，四边形OA1B1C1，A1A2B2C2，A2A3B3C3，都是菱形，点A1，A2，A3，…，都在x轴上，点C1，C2，C3，…都在直线y=33x+33上，且∠C1OA1=∠C2A1A2=∠C3A2A3=⋅⋅⋅=60°，OA1=1则点B2023的坐标是 ．
【变式11-2】（2023·重庆沙坪坝·重庆南开中学校考二模）如图，在菱形ABCD中，对角线AC，BD交于点O，AC=6，BD=4，动点P从点A出发，沿着折线A→O→B运动，速度为每秒1个单位长度，到达B点停止运动，设点P的运动时间为t秒，△PAD的面积为y．

(1)直接写出y关于t的函数表达式，并注明自变量t的取值范围；
(2)在直角坐标系中画出y与t的函数图象，并写出它的一条性质；
(3)根据图象直接写出当y≤4时t的取值范围．
【变式11-3】（2023·安徽滁州·校考模拟预测）如图，在平面直角坐标系中，直线l1:y=-12x+6分别与x轴、y轴交于点B、C，且与直线l2:y=12x交于点A．
(1)分别求出点A、B、C的坐标；
(2)若D是线段OA上的点，且△COD的面积为12，求直线CD的函数表达式；
(3)在2的条件下，设P是射线CD上的点，在平面内是否存在点Q，使以O、C、P、Q为顶点的四边形是菱形？若存在，直接写出点Q的坐标．
【题型12 菱形与反比例函数综合】
【例12】（2023·浙江嘉兴·统考二模）如图，平面直角坐标系中，菱形ABCD的顶点A,C在反比例函数y=kx(k0与菱形的边BC交于点E．

(1)求点C的坐标和反比例函数y=kxx>0的表达式；
(2)如图2，连接OC，OE求出△COE的面积；
(3)点P为y=kxx>0图像上的一动点，过点P做PH⊥x轴于点H，若点P使得△AOM和△BPH相似，请直接写出点P的横坐标．
【题型13 菱形与一次函数、反比例函数综合】
【例13】（2023·江西鹰潭·统考二模）如图，一次函数y=-13x-2的图象分别交x轴、y轴于A、B两点，P为AB的中点，PC⊥x轴于点C，延长PC交反比例函数y=kxx0的图像相交于A3,4，B-4,n两点，与x轴相交于点C．

(1)求m和n的值；
(2)若点Pe,f在该反比例函数的图像上，且它到y轴的距离小于3，则f的取值范围是 ；（直接写出答案）
(3)以AC为边在右侧作菱形ACDE．使点D在x轴正半轴上，点E在第一象限，双曲线交DE于点F，连接AF,CF，则△ACF的面积为 ．（直接写出答案）
【变式13-3】（2023·广东佛山·校考一模）如图，点A在双曲线y=kx（k>0，x>0）上，点B在直线l：y=mx-2b（m>0，b>0）上，A与B关于x轴对称，直线l与y轴交于点C，当四边形AOCB是菱形时，有以下结论：①Ab,3b②当b=2时，k=43③m=33④S四边形AOCB=2b2则所有正确结论的序号是 ．
【题型14 菱形与二次函数综合】
【例14】（2023·山东青岛·统考二模）如图1，在菱形ABCD中，AC、BD交于点E，BD=16厘米，点F在CE上，EF=3厘米．点P、Q分别从A、E两点同时出发，点P以k厘米/秒的速度沿AE向点E匀速运动，用时8秒到达点E；点Q以m厘米/秒的速度沿EB向点E匀速运动，设运动的时间为x秒0≤x≤8，△EFQ的面积为y1平方厘米，△PEQ的面积为y2平方厘米．

(1)图2中的线段OH是y1与x的函数图象，则y1与x的函数关系式为________，m的值为________；
(2)图2中的抛物线是y2与x的函数图象，其顶点坐标是4,12，求点P的速度及对角线AC的长；
(3)在图2中，点G是x轴正半轴上一点（0