

所属成套资源:2025年中考数学一轮复习核心考点精讲 (2份,原卷版+解析版)
2025年中考数学一轮复习核心考点精讲专题28 轴对称、平移、旋转(2份,原卷版+解析版)
展开
这是一份2025年中考数学一轮复习核心考点精讲专题28 轴对称、平移、旋转(2份,原卷版+解析版),文件包含2025年中考数学一轮复习核心考点精讲专题28轴对称平移旋转原卷版docx、2025年中考数学一轮复习核心考点精讲专题28轴对称平移旋转解析版docx等2份试卷配套教学资源,其中试卷共61页, 欢迎下载使用。
1.理解轴对称图形与中心对称图形概念;
2.掌握图形的平移的性质及有关计算;
3.掌握图形的旋转性质并运用其性质进行有关的计算;
4.掌握位似的性质。
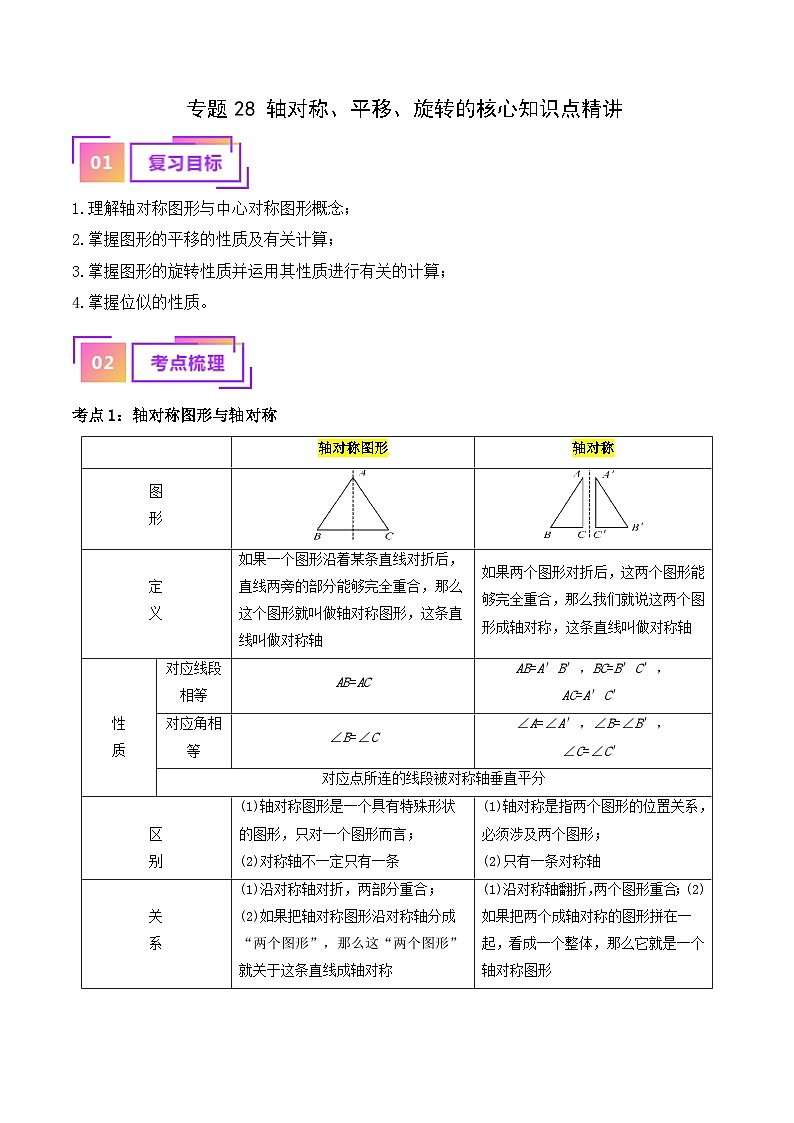
考点1:轴对称图形与轴对称
1.常见的轴对称图形: 等腰三角形、矩形、菱形、正方形、圆.
2.折叠的性质:折叠的实质是轴对称,折叠前后的两图形全等,对应边和对应角相等.
3.作某点关于某直线的对称点的一般步骤
1)过已知点作已知直线(对称轴)的垂线,标出垂足;2)在这条直线另一侧从垂足除法截取与已知点到垂足的距离相等的线段,那么截点就是这点关于该直线的对称点.
4.作已知图形关于某直线的对称图形的一般步骤
1)作出图形的关键点关于这条直线的对称点;
2)把这些对称点顺次连接起来,就形成了一个符合条件的对称图形.
考点2:图形的平移
1.定义:在平面内,一个图形由一个位置沿某个方向移动到另一个位置,这样的图形运动叫做平移.平移不改变图形的形状和大小.
2.三大要素: 一是平移的起点,二是平移的方向,三是平移的距离.
3.性质:
1)平移前后,对应线段平行且相等、对应角相等;2)各对应点所连接的线段平行(或在同一条直线上)且相等;3)平移前后的图形全等.
4.作图步骤:
1)根据题意,确定平移的方向和平移的距离;2)找出原图形的关键点;3)按平移方向和平移距离平移各个关键点,得到各关键点的对应点;4)按原图形依次连接对应点,得到平移后的图形.
考点3:图形的旋转
1.定义:在平面内,一个图形绕一个定点沿某个方向(顺时针或逆时针)转过一个角度,这样的图形运动叫旋转.这个定点叫做旋转中心,转过的这个角叫做旋转角.
2.三大要素:旋转中心、旋转方向和旋转角度.
3.性质:
1)对应点到旋转中心的距离相等;2)每对对应点与旋转中心所连线段的夹角等于旋转角;
3)旋转前后的图形全等.
4.作图步骤:1)根据题意,确定旋转中心、旋转方向及旋转角;2)找出原图形的关键点;3)连接关键点与旋转中心,按旋转方向与旋转角将它们旋转,得到各关键点的对应点;4)按原图形依次连接对应点,得到旋转后的图形.
【注意】旋转是一种全等变换,旋转改变的是图形的位置,图形的大小关系不发生改变,所以在解答有关旋转的问题时,要注意挖掘相等线段、角,因此特殊三角形性质的运用、锐角三角函数建立的边角关系起着关键的作用.
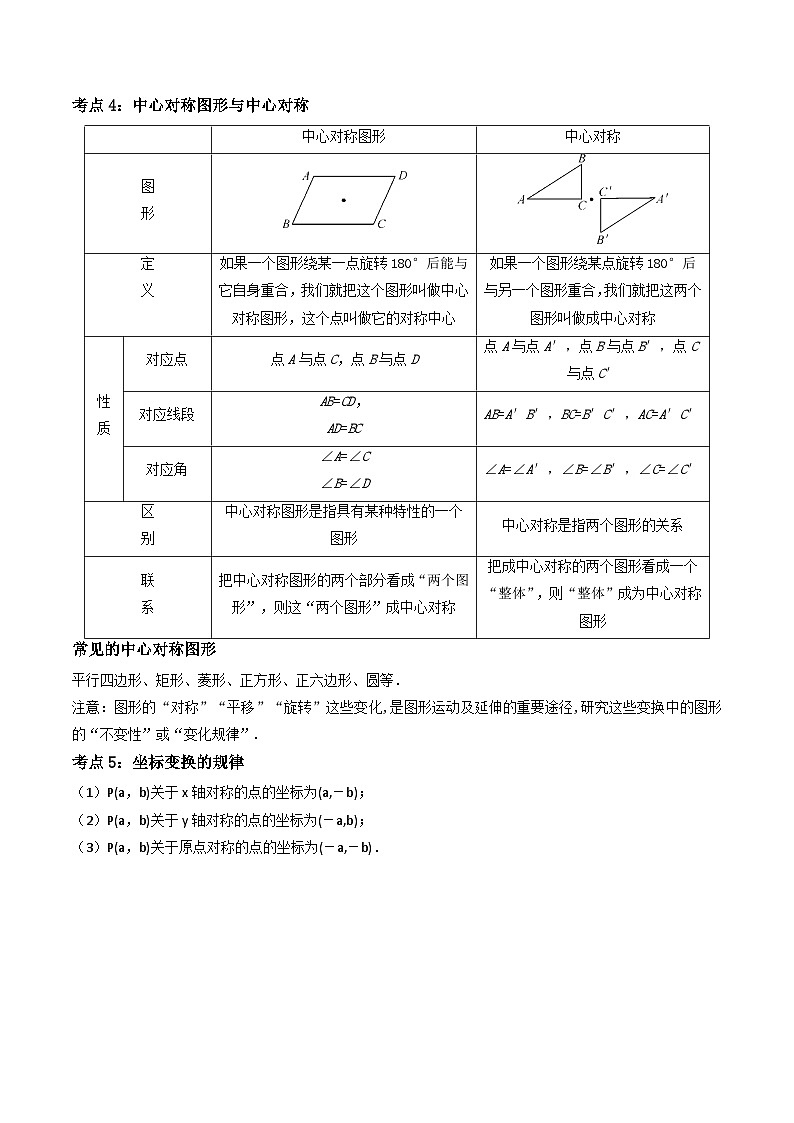
考点4:中心对称图形与中心对称
常见的中心对称图形
平行四边形、矩形、菱形、正方形、正六边形、圆等.
注意:图形的“对称”“平移”“旋转”这些变化,是图形运动及延伸的重要途径,研究这些变换中的图形的“不变性”或“变化规律”.
考点5:坐标变换的规律
(1)P(a,b)关于x轴对称的点的坐标为(a,-b);
(2)P(a,b)关于y轴对称的点的坐标为(-a,b);
(3)P(a,b)关于原点对称的点的坐标为(-a,-b).
【题型1:平移、旋转与轴对称的识别】
【典例1】(2023•苏州)古典园林中的花窗通常利用对称构图,体现对称美.下面四个花窗图案,既是轴对称图形又是中心对称图形的是( )
A.B.
C.D.
【变式1-1】(2023•泰州)书法是我国特有的优秀传统文化,其中篆书具有象形特征,充满美感.下列“福”字的四种篆书图案中,可以看作轴对称图形的是( )
A.B.C.D.
【变式1-2】(2023•广西)下列数学经典图形中,是中心对称图形的是( )
A. B.C.D.
【变式1-3】(2023•宜昌)我国古代数学的许多创新与发明都曾在世界上有重要影响.下列图形“杨辉三角”“中国七巧板”“刘徽割圆术”“赵爽弦图”中,中心对称图形是( )
A.B.
C.D.
【题型2:平移、旋转与轴对称性质的应用】
【典例2】(2023•无锡)如图,△ABC中,∠BAC=55°,将△ABC逆时针旋转α(0°<α<55°),得到△ADE,DE交AC于F.当α=40°时,点D恰好落在BC上,此时∠AFE等于( )
A.80°B.85°C.90°D.95°
【变式2-1】(2023•南充)如图,将△ABC沿BC向右平移得到△DEF,若BC=5,BE=2,则CF的长是( )
A.2B.2.5C.3D.5
【变式2-2】(2023•牡丹江)在以“矩形的折叠”为主题的数学活动课上,某位同学进行了如下操作:
第一步:将矩形纸片的一端,利用图①的方法折出一个正方形ABEF,然后把纸片展平;
第二步:将图①中的矩形纸片折叠,使点C恰好落在点F处,得到折痕MN,如图②.
根据以上的操作,若AB=8,AD=12,则线段BM的长是( )
A.3B.C.2D.1
【变式2-3】(2023•宁夏)如图,在△ABC中,∠BAC=90°,AB=AC,BC=2.点D在BC上,且BD:CD=1:3.连接AD,线段AD绕点A顺时针旋转90°得到线段AE,连接BE,DE.则△BDE的面积是( )
A.B.C.D.
【题型3:图形变化与点坐标变化】
【典例3】(2023•海南)如图,在平面直角坐标系中,点A在y轴上,点B的坐标为(6,0),将△ABO绕着点B顺时针旋转60°,得到△DBC,则点C的坐标是( )
A.(3,3)B.(3,3)C.(6,3)D.(3,6)
【变式3-1】(2023•金华)如图,两盏灯笼的位置A,B的坐标分别是(﹣3,3),(1,2),将点B向右平移2个单位,再向上平移1个单位得到点B′,则关于点A,B′的位置描述正确的是( )
A.关于x轴对称B.关于y轴对称
C.关于原点O对称D.关于直线y=x对称
【变式3-2】(2023•青岛)如图,将线段AB先向左平移,使点B与原点O重合,再将所得线段绕原点旋转180°得到线段A′B′,则点A的对应点A′的坐标是( )
A.(2,﹣3)B.(﹣2,3)C.(3,﹣2)D.(﹣3,2)
【变式3-3】(2023•聊城)如图,在直角坐标系中,△ABC各点坐标分别为A(﹣2,1),B(﹣1,3),C(﹣4,4).先作△ABC关于x轴成轴对称的△A1B1C1,再把△A1B1C1平移后得到△A2B2C2.若B2(2,1),则点A2坐标为( )
A.(1,5)B.(1,3)C.(5,3)D.(5,5)
【变式3-4】(2023•朝阳)如图,在平面直角坐标系中,已知点A(2,2),B(4,1),以原点O为位似中心,相似比为2,把△OAB放大,则点A的对应点A′的坐标是( )
A.(1,1)B.(4,4)或(8,2)
C.(4,4)D.(4,4)或(﹣4,﹣4)
【题型4:与平移、旋转与轴对称相关的网格作图】
【典例4】(2023•达州)如图,网格中每个小正方形的边长均为1,△ABC的顶点均在小正方形的格点上.
(1)将△ABC向下平移3个单位长度得到△A1B1C1,画出△A1B1C1;
(2)将△ABC绕点C顺时针旋转90度得到△A2B2C2,画出△A2B2C2;
(3)在(2)的运动过程中请计算出△ABC扫过的面积.
【变式4-1】(2023•宜昌)如图,在方格纸中按要求画图,并完成填空.
(1)画出线段OA绕点O顺时针旋转90°后得到的线段OB,连接AB;
(2)画出与△AOB关于直线OB对称的图形,点A的对称点是C;
(3)填空:∠OCB的度数为 .
【变式4-2】(2023•宁波)在4×4的方格纸中,请按下列要求画出格点三角形(顶点均在格点上).
【变式4-3】(2023•黑龙江)如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(2,﹣1),B(1,﹣2),C(3,﹣3).
(1)将△ABC向上平移4个单位,再向右平移1个单位,得到△A1B1C1,请画出△A1B1C1;
(2)请画出△ABC关于y轴对称的△A2B2C2;
(3)将△A2B2C2绕着原点O顺时针旋转90°,得到△A3B3C3,求线段A2C2在旋转过程中扫过的面积(结果保留π).
一.选择题(共8小题)
1.在学习图案与设计这一节课时,老师要求同学们利用图形变化设计图案,下列设计的图案中既是中心对称图形又是轴对称图形的是( )
A. B.C. D.
2.在《生活中的平移现象》的数学讨论课上,小明和小红先将一块三角板描边得到△ABC,后沿着直尺BC方向平移3cm,再描边得到到△DEF,连接AD.如图,经测量发现△ABC的周长为16cm,则四边形ABFD的周长为( )
A.16cmB.22cmC.20cmD.24cm
3.如图,△ABC与△A'B'C'关于直线l对称,连接AA',BB',CC',其中BB′分别交AC,A′C于点D,D',下列结论:①AA'∥BB';②∠ADB=∠A′D′B′;③直线l垂直平分 AA';④直线AB与A'B'的交点不一定在直线l上.其中正确的是( )
A.①②③B.②③④C.①②④D.①③④
4.如图,在长方形ABCD中,AB=5,BC=3,将长方形沿BE折叠,使得点A落在CD边上F处,则AE的长是( )
A.B.C.D.2
5.如图,将△ABC绕点A逆时针旋转30°得到△AB′C′,若∠C′=45°,且AB′⊥BC于点E,则∠BAC的度数为( )
A.60°B.75°C.45°D.50°
6.如图,点E是正方形ABCD的边DC上一点,把△ADE绕点A顺时针旋转90°到△ABF的位置.若四边形AECF的面积为36,DE=2,则AF的长为( )
A.6B.C.8D.
7.如图,Rt△ABC中,∠ACB=90°,BC=4,AC=3,将△ABC绕点B逆时针旋转得△A'BC',若点C'在AB上,则AA'的长为( )
A.B.4C.D.5
8.如图,在等腰△AOB中,OA=AB,∠OAB=120°,OA边在x轴上,将△AOB绕原点O逆时针旋转120°,得到△A'OB',若,则点A的对应点A'的坐标为( )
A.(﹣1,﹣1)B.(﹣1,)C.(﹣1,2)D.(﹣1,)
二.填空题(共7小题)
9.若点A(2,﹣3)关于坐标原点的对称点是B,则点B的坐标为 .
10.如图,已知四边形ABCD是长方形,点E、F分别在线段AB、CD上,将四边形AEFD沿EF翻折得到四边形A'EFD',若∠CFD'=36°,则∠DFE= .
11.如图,将长为6,宽为4的长方形ABCD先向右平移2,再向下平移1,得到长方形A'B'CD',则阴影部分的面积为 .
12.线段AB两端点的坐标分别为A(2,4),B(5,2),若将线段AB平移,使得点B的对应点为点C(3,﹣1).则平移后点A的对应点的坐标为 .
13.如图,有一块长方形区域,AD=2AB,现在其中修建两条长方形小路,每条小路的宽度均为1米,设AB边的长为x米,则图中空白区域的面积为 .
14.如图,在Rt△ABC中,∠BAC=30°,BC=3,将△ABC绕点A顺时针旋转90°得到△AB′C′,则BB′= .
15.如图,在平面直角坐标系中,将点P(2,3)绕原点O旋转90°得到点P′,则点P′的坐标为 .
三.解答题(共3小题)
16.如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).
(1)请画出△ABC绕点O逆时针旋转90°后的△A1B1C1,并写出A1的坐标;
(2)求(1)中C点旋转到C1点所经过的路径长(结果保留π).
17.如图所示,点O是等边△ABC内的任一点,连接OA,OB,OC,∠AOB=150°,∠BOC=120°,将△BOC绕点C按顺时针方向旋转60°得△ADC.
(1)求∠DAO的度数;
(2)用等式表示线段OA,OB,OC之间的数量关系,并证明.
18.如图,在△ABC中,∠ACB=90°,AC=BC,D是AB边上一点(点D与A,B不重合),连结CD,将线段CD绕点C逆时针旋转90°得到线段CE,连结DE交BC于点F,连接BE.
(1)求证:△ACD≌△BCE;
(2)当∠BDE=25°时,求∠BEF的度数.
一.选择题(共7小题)
1.如图,将长方形ABCO放置于平面直角坐标系中,点O与原点重合,点A,C分别在y轴和x轴上,点B(8,4),连接BO,并将△ABO沿BO翻折至长方形ABCO所在平面,点A的对称点为点E,则点E的坐标为( )
A.B.
C.D.
2.如图,将周长为8的△ABC沿BC方向向右平移2个单位长度得到△DEF,则四边形ABFD的周长为( )
A.10B.12C.14D.16
3.如图,正方形ABCD,边长AB=2,对角线AC、BD相交于点O,将直角三角板的直角顶点放在点O处,三角板两边足够长,与BC、CD交于E、F两点,当三角板绕点O旋转时,线段EF的最小值为( )
A.1B.2C.D.2
4.如图,平面直角坐标系中,点B在第一象限,点A在x轴的正半轴上,∠AOB=∠B=30°,OA=2.将△AOB绕点O逆时针旋转90°,点B的对应点B'的坐标是( )
A.B.C.D.
5.如图,菱形ABCD,点A,B,C,D均在坐标轴上,∠ADC=120°,点A的坐标为(﹣4,0),点E是CD的中点,点P是OC上的一动点,则PD+PE的最小值是( )
A.4B.C.D.
6.如图,将正方形纸片ABCD沿PQ折叠,使点C的对称点E落在边AB上,点D的对称点为点F,EF为交AD于点G,连接CG交PQ于点H,连接CE.下列四个结论中:①△PBE∽△QFG;②S△CEG=S△CBE+S四边形CDQH;③EC平分∠BEG;④EG2﹣CH2=GQ•GD,正确的是( )
A.①②③B.①③④C.①②④D.②③④
7.如图,在矩形ABCD中,AB=8,BC=10,点E、F分别是边AB、BC上一动点,将△BEF沿EF折叠,若点B恰好落在AD边上的点G处,设EF=x,则x的取值范围为( )
A.B.C.D.
二.填空题(共6小题)
8.如图,在Rt△ABC中,∠ABC=90°,∠C=65°,将△ABC绕点B逆时针旋转至△EBD,使点C落在边AC上的D处,则∠EBA= .
9.如图,将△ABC绕点A顺时针旋转60°得到△AED,若线段AB=5,则BE的长度为 .
10.如图,△ABC中,∠CAB=70°,在同一平面内,将△ABC绕点A旋转到△AED的位置,使CD∥AB,则∠BAE的度数为 .
11.如图,在等边△ABC中,AB=6,点P是边BC上的动点,将△ABP绕点A逆时针旋转60°得到△ACQ,点D是AC边的中点,连接DQ,则DQ的最小值是 .
12.如图,正方形ABCD中,AB=4,点P为射线AD上一个动点.连接BP,把△ABP沿BP折叠,当点A的对应点A'刚好落在线段BC的垂直平分线上时,AP的长为 .
13.如图,已知四边形ABCD是边长为4的正方形,点E是BC边的中点,连接DE,将△DCE沿DE翻折得到△DC'E,连接AC′,则AC′的长为 .
三.解答题(共2小题)
14.如图,在△ABC中,∠ACB=30°,将△ABC绕点C顺时针旋转60°得到△DEC,连接AE.求证:AB=AE.
15.[教材呈现]下面是华师版九年级上册数学教材第76页的部分内容.
如图,E是矩形ABCD的边CB上的一点,AF⊥DE于点F,AB=3,AD=2,CE=1,证明△AFD∽△DCE,并计算点A到直线DE的距离(结果保留根号).
结合图①,完成解答过程.
[拓展]
(1)在图①的基础上,延长线段AF交边CD于点G,如图②,则FG的长为 ;
(2)如图③,E、F是矩形ABCD的边AB、CD上的点,连结EF,将矩形ABCD沿EF翻折,使点D的对称点D'与点B重合,点A的对称点为点A'.若AB=4,AD=3,则EF的长为 .
1.(2023•常州)在平面直角坐标系中,若点P的坐标为(2,1),则点P关于y轴对称的点的坐标为( )
A.(﹣2,﹣1)B.(2,﹣1)C.(﹣2,1)D.(2,1)
2.(2023•自贡)下列交通标志图案中,既是中心对称图形又是轴对称图形的是( )
A. B. C. D.
3.(2023•天津)如图,把△ABC以点A为中心逆时针旋转得到△ADE,点B,C的对应点分别是点D,E,且点E在BC的延长线上,连接BD,则下列结论一定正确的是( )
A.∠CAE=∠BED B.AB=AEC.∠ACE=∠ADE D.CE=BD
4.(2023•通辽)如图,将△ABC绕点A逆时针旋转到△ADE,旋转角为α(0°<α<180°),点B的对应点D恰好落在BC边上,若DE⊥AC,∠CAD=24°,则旋转角α的度数为( )
A.24°B.28°C.48°D.66°
5.(2023•黄石)如图,已知点A(1,0),B(4,m),若将线段AB平移至CD,其中点C(﹣2,1),D(a,n),则m﹣n的值为( )
A.﹣3B.﹣1C.1D.3
6.(2023•绍兴)在平面直角坐标系中,将点(m,n)先向右平移2个单位,再向上平移1个单位,最后所得点的坐标是( )
A.(m﹣2,n﹣1)B.(m﹣2,n+1)C.(m+2,n﹣1)D.(m+2,n+1)
7.(2022•福建)如图,现有一把直尺和一块三角尺,其中∠ABC=90°,∠CAB=60°,AB=8,点A对应直尺的刻度为12.将该三角尺沿着直尺边缘平移,使得△ABC移动到△A′B′C′,点A′对应直尺的刻度为0,则四边形ACC′A′的面积是( )
A.96B.96C.192D.160
8.(2022•张家界)如图所示的方格纸(1格长为一个单位长度)中,△AOB的顶点坐标分别为A(3,0),O(0,0),B(3,4).
(1)将△AOB沿x轴向左平移5个单位,画出平移后的△A1O1B1(不写作法,但要标出顶点字母);
(2)将△AOB绕点O顺时针旋转90°,画出旋转后的△A2O2B2(不写作法,但要标出顶点字母);
(3)在(2)的条件下,求点B绕点O旋转到点B2所经过的路径长(结果保留π).
轴对称图形
轴对称
图
形
定
义
如果一个图形沿着某条直线对折后,直线两旁的部分能够完全重合,那么这个图形就叫做轴对称图形,这条直线叫做对称轴
如果两个图形对折后,这两个图形能够完全重合,那么我们就说这两个图形成轴对称,这条直线叫做对称轴
性
质
对应线段相等
AB=AC
AB=A′B′,BC=B′C′,
AC=A′C′
对应角相等
∠B=∠C
∠A=∠A′,∠B=∠B′,
∠C=∠C′
对应点所连的线段被对称轴垂直平分
区
别
(1)轴对称图形是一个具有特殊形状的图形,只对一个图形而言;
(2)对称轴不一定只有一条
(1)轴对称是指两个图形的位置关系,必须涉及两个图形;
(2)只有一条对称轴
关
系
(1)沿对称轴对折,两部分重合;
(2)如果把轴对称图形沿对称轴分成“两个图形”,那么这“两个图形”就关于这条直线成轴对称
(1)沿对称轴翻折,两个图形重合;(2)如果把两个成轴对称的图形拼在一起,看成一个整体,那么它就是一个轴对称图形
中心对称图形
中心对称
图
形
定
义
如果一个图形绕某一点旋转180°后能与它自身重合,我们就把这个图形叫做中心对称图形,这个点叫做它的对称中心
如果一个图形绕某点旋转180°后与另一个图形重合,我们就把这两个图形叫做成中心对称
性
质
对应点
点A与点C,点B与点D
点A与点A′,点B与点B′,点C与点C′
对应线段
AB=CD,
AD=BC
AB=A′B′,BC=B′C′,AC=A′C′
对应角
∠A=∠C
∠B=∠D
∠A=∠A′,∠B=∠B′,∠C=∠C′
区
别
中心对称图形是指具有某种特性的一个图形
中心对称是指两个图形的关系
联
系
把中心对称图形的两个部分看成“两个图形”,则这“两个图形”成中心对称
把成中心对称的两个图形看成一个“整体”,则“整体”成为中心对称图形
相关试卷
这是一份考点22图形的变换(平移、旋转、轴对称)(精讲)-2024年中考数学一轮复习之核心考点精讲精练(全国通用)原卷版+解析版,文件包含考点22图形的变换平移旋转轴对称精讲原卷版docx、考点22图形的变换平移旋转轴对称精讲解析版docx等2份试卷配套教学资源,其中试卷共68页, 欢迎下载使用。
这是一份考点22图形的变换(平移、旋转、轴对称)(精练)-2024年中考数学一轮复习之核心考点精讲精练(全国通用)原卷版+解析版,文件包含考点22图形的变换平移旋转轴对称精练原卷版-2024年中考数学一轮复习之核心考点精讲精练全国通用docx、考点22图形的变换平移旋转轴对称精练解析版docx等2份试卷配套教学资源,其中试卷共57页, 欢迎下载使用。
这是一份中考数学一轮复习考点过关练习专题28 轴对称、平移、旋转的核心知识点精讲(讲义)(2份打包,原卷版+含解析),文件包含中考数学一轮复习考点过关练习专题28轴对称平移旋转的核心知识点精讲讲义原卷版全国通用doc、中考数学一轮复习考点过关练习专题28轴对称平移旋转的核心知识点精讲讲义含解析全国通用doc等2份试卷配套教学资源,其中试卷共61页, 欢迎下载使用。










