2025年中考数学一轮复习精品讲义第02讲 整式与因式分解（2份，原卷版+解析版）

这是一份2025年中考数学一轮复习精品讲义第02讲 整式与因式分解（2份，原卷版+解析版），文件包含2025年中考数学一轮复习精品讲义第02讲整式与因式分解原卷版docx、2025年中考数学一轮复习精品讲义第02讲整式与因式分解解析版docx等2份试卷配套教学资源，其中试卷共82页， 欢迎下载使用。

TOC \ "1-3" \h \z \u \l "_Tc150724342" 一、考情分析
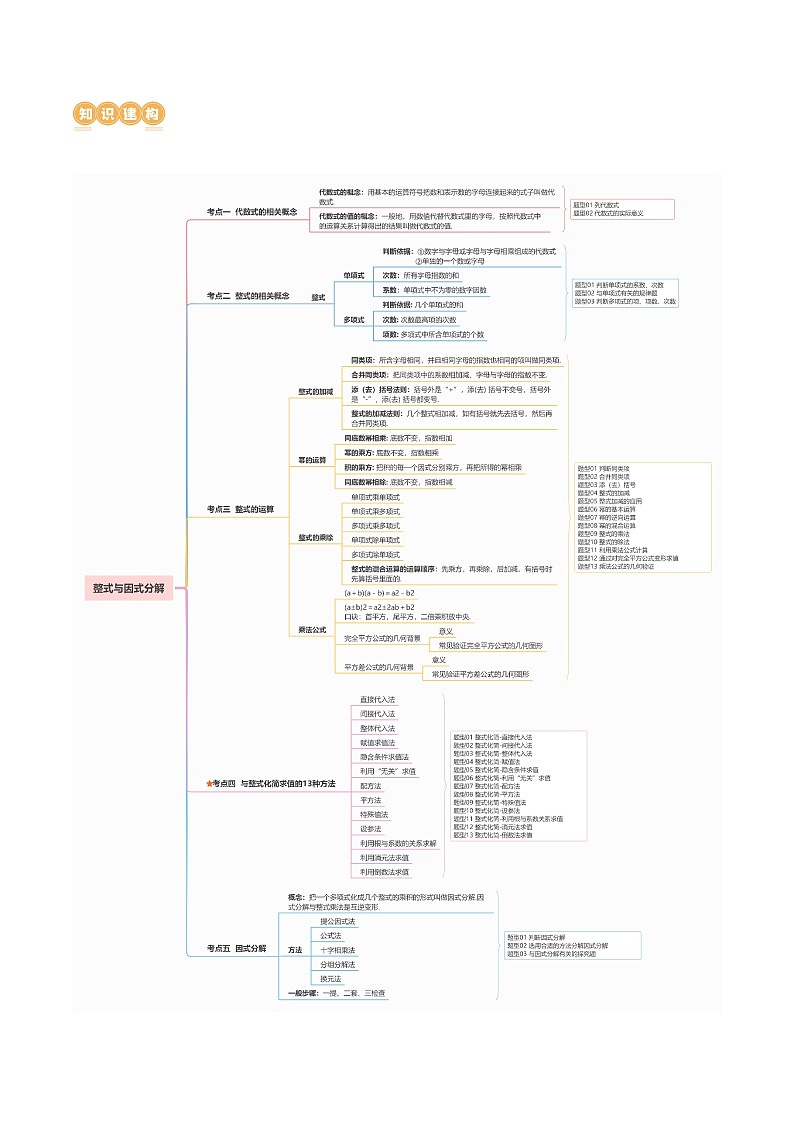
二、知识建构
\l "_Tc150724343" 考点一 代数式的相关概念 PAGEREF _Tc150724343 \h 4
\l "_Tc150724344" 题型01 列代数式 PAGEREF _Tc150724344 \h 4
\l "_Tc150724345" 题型02 代数式的实际意义 PAGEREF _Tc150724345 \h 4
\l "_Tc150724346" 考点二 整式的相关概念 PAGEREF _Tc150724346 \h 5
\l "_Tc150724347" 题型01 判断单项式的系数、次数 PAGEREF _Tc150724347 \h 5
\l "_Tc150724348" 题型02 与单项式有关的规律题 PAGEREF _Tc150724348 \h 6
\l "_Tc150724349" 题型03 判断多项式的项、项数、次数 PAGEREF _Tc150724349 \h 6
\l "_Tc150724350" 考点三 整式的运算 PAGEREF _Tc150724350 \h 7
\l "_Tc150724351" 题型01 判断同类项 PAGEREF _Tc150724351 \h 10
\l "_Tc150724352" 题型02 合并同类项 PAGEREF _Tc150724352 \h 11
\l "_Tc150724353" 题型03 添（去）括号 PAGEREF _Tc150724353 \h 11
\l "_Tc150724354" 题型04 整式的加减 PAGEREF _Tc150724354 \h 11
\l "_Tc150724355" 题型05 整式加减的应用 PAGEREF _Tc150724355 \h 12
\l "_Tc150724356" 题型06 幂的基本运算 PAGEREF _Tc150724356 \h 13
\l "_Tc150724357" 题型07 幂的逆向运算 PAGEREF _Tc150724357 \h 14
\l "_Tc150724358" 题型08 幂的混合运算 PAGEREF _Tc150724358 \h 14
\l "_Tc150724359" 题型09 整式的乘法 PAGEREF _Tc150724359 \h 15
\l "_Tc150724360" 题型10 整式的除法 PAGEREF _Tc150724360 \h 15
\l "_Tc150724361" 题型11 利用乘法公式计算 PAGEREF _Tc150724361 \h 16
\l "_Tc150724362" 题型12 通过对完全平方公式变形求值 PAGEREF _Tc150724362 \h 16
\l "_Tc150724363" 题型13 乘法公式的几何验证 PAGEREF _Tc150724363 \h 17
\l "_Tc150724364" 考点四 整式化简求值（高频考点） PAGEREF _Tc150724364 \h 19
\l "_Tc150724365" 题型01 整式化简-直接代入法 PAGEREF _Tc150724365 \h 20
\l "_Tc150724366" 题型02 整式化简-间接代入法 PAGEREF _Tc150724366 \h 20
\l "_Tc150724367" 题型03 整式化简-整体代入法 PAGEREF _Tc150724367 \h 20
\l "_Tc150724368" 题型04 整式化简-赋值法 PAGEREF _Tc150724368 \h 20
\l "_Tc150724369" 题型05 整式化简-隐含条件求值 PAGEREF _Tc150724369 \h 21
\l "_Tc150724370" 题型06 整式化简-利用“无关”求值 PAGEREF _Tc150724370 \h 21
\l "_Tc150724371" 题型07 整式化简-配方法 PAGEREF _Tc150724371 \h 21
\l "_Tc150724372" 题型08 整式化简-平方法 PAGEREF _Tc150724372 \h 21
\l "_Tc150724373" 题型09 整式化简-特殊值法 PAGEREF _Tc150724373 \h 21
\l "_Tc150724374" 题型10 整式化简-设参法 PAGEREF _Tc150724374 \h 22
\l "_Tc150724375" 题型11 整式化简-利用根与系数关系求值 PAGEREF _Tc150724375 \h 22
\l "_Tc150724376" 题型12 整式化简-消元法求值 PAGEREF _Tc150724376 \h 22
\l "_Tc150724377" 题型13 整式化简-倒数法求值 PAGEREF _Tc150724377 \h 22
\l "_Tc150724378" 考点五 因式分解 PAGEREF _Tc150724378 \h 22
\l "_Tc150724379" 题型01 判断因式分解 PAGEREF _Tc150724379 \h 23
\l "_Tc150724380" 题型02 选用合适的方法因式分解 PAGEREF _Tc150724380 \h 24
\l "_Tc150724381" 题型03 与因式分解有关的探究题 PAGEREF _Tc150724381 \h 24
考点一 代数式的相关概念
代数式的概念：用基本的运算符号把数和表示数的字母连接起来的式子叫做代数式.
代数式的值的概念：一般地，用数值代替代数式里的字母，按照代数式中的运算关系计算得出的结果叫做代数式的值.
1. 代数式中不含有=、<、>、≠等.
2. 单独的一个数或一个字母也是代数式.
3. 列代数式时注意事项：
①仔细辨别词义． 列代数式时，要先认真审题，抓住关键词语，仔细辨析词义．如“除”与“除以”，“平方的差（或平方差）”与“差的平方”的词义区分．
②分清数量关系．要正确列代数式，只有分清数量之间的关系．
③注意运算顺序．列代数式时，一般应在语言叙述的数量关系中，先读的先写，不同级运算的语言，且又要体现出先低级运算，要把代数式中代表低级运算的这部分用括号括起来．
④规范书写格式．列代数时要按要求规范地书写．像数字与字母、字母与字母相乘可省略乘号不写，数与数相乘必须写乘号；除法可写成分数形式，带分数与字母相乘需把代分数化为假分数，书写单位名称什么时不加括号，什么时要加括号．注意代数式括号的适当运用．
⑤正确进行代换．列代数式时，有时需将题中的字母代入公式，这就要求正确进行代换．
题型01 列代数式
【例1】（2023吉林长春中考真题）2023长春马拉松于5月21日在南岭体育场鸣枪开跑，某同学参加了7.5公里健康跑项目，他从起点开始以平均每分钟x公里的速度跑了10分钟，此时他离健康跑终点的路程为 公里．（用含x的代数式表示）
【变式1-1】（2023江苏中考真题）若圆柱的底面半径和高均为 QUOTE a a，则它的体积是 （用含 QUOTE a a的代数式表示）．
题型02 代数式的实际意义
【例2】（2023河北中考真题）代数式 QUOTE -7x -7x的意义可以是（ ）
A． -7与x的和B．-7与x的差C．-7与x的积D．-7与x的商
【变式2-1】（2020·内蒙古通辽·中考真题）下列说法不正确的是( )
A． QUOTE 2a 2a是2个数a的和B． QUOTE 2a 2a是2和数a的积
C． QUOTE 2a 2a是单项式D． QUOTE 2a 2a是偶数
考点二 整式的相关概念
1.由定义可知，单项式中只含有乘法运算.
2.一个单项式中只含有字母因数时，它的系数是1或者-1，不能认为是0. 一个单项式是一个常数时，它的系数就是它本身.确定一个单项式的系数，要注意包含在它前面的符号.例如：-（3x）的系数是-3.
3.圆周率 SKIPIF 1 < 0 π是常数，当它出现在单项式中时，应将其作为系数的一部分，而不能当成字母.
4.单项式的指数只和字母的指数有关，与系数的指数无关.如单项式－25x2y3z4的次数是2＋3＋4=9而不是14.
5.由定义可知，多项式中可以含有:乘法、加法、减法运算.
6. 多项式有统一的次数，但是没有统一的系数，多项式中的每一项有自己的系数.
7. 多项式通常以它的次数和项数来命名，称几次（最高次项的次数）几项（多项式项数）式.
题型01 判断单项式的系数、次数
【例1】（2023·江西·统考中考真题）单项式 QUOTE -5ab -5ab的系数为 ．
【变式1-1】（2023·广东·模拟预测）单项式-πxy32的系数是 ．
【变式1-2】（2023·广东·统考模拟预测）已知一个单项式的系数是2，次数是3，则这个单项式可以是（ ）
A．-2xy2B．3x2C．2xy3D．2x3
题型02 与单项式有关的规律题
【例2】（2023·云南·统考中考真题）按一定规律排列的单项式：，第n个单项式是（ ）A．nB．C．D．
【变式2-1】（2022·云南·中考真题）按一定规律排列的单项式：x，3x2，5x3，7x4，9x5，……，第n个单项式是（ ）
A．(2n-1)xnB．(2n+1)xnC．(n-1)xnD．(n+1)xn
【变式2-2】（2022·云南昆明·统考三模）按一定规律排列的代数式：2，-4x2，8x4，-16x6，32x8，……，第n个单项式是（ ）
A．-1n2nx2n-2B．-1n-12nx2n-2C．-1n-12nx2nD．-1n-12nx2n-2
【变式2-3】（2022·云南昆明·昆明市一模）按一定规律排列的单项式：3b2，5a2b2，7a4b2，，11a8b2，…，第8个单项式是（ ）
A．17a14b2B．17a8b4C．15a7b14D．152a14b2
【变式2-4】（2022·云南文山·统考二模）一组按规律排列的单项式：-4x，7x2，，13x4，-16x5，…，根据其中的规律，第12个单项式是（ ）
A．-31x12B．34x12C．37x12D．-40x11
通过观察与归纳，分别找出单项式的系数和次数的规律是解决此类问题的关键．
题型03 判断多项式的项、项数、次数
【例3】（2023·广东茂名一模）多项式a3+2ab+a-3的次数和常数项分别是( )A．6，3B．6，-3C．3，-3D．3，3
【变式3-1】（2023·江西赣州市模拟预测）下列说法正确的是（ ）
A．2πmn的系数是2πB．-82ab2的次数是5次
C．xy3+3x2y-4的常数项为4D．11x2-6x+5是三次三项式
【变式3-2】（2023·广东茂名·校考一模）多项式ab-13πa2b+3最高次项的系数是 ，次数是 ．
考点三 整式的运算
1.所有常数项都是同类项.
2.“同类项口诀”：①两同两无关，识别同类项: ②一相加二不变，合并同类项.
“两同”：一是所含字母相同；二是相同字母的指数也相同，这两点也是判断同类项的标准，缺一不可.
“两无关”：一是与系数大小无关；二是与所含字母的顺序无关.
“一相加”：系数相加作为结果的系数.“二不变”：字母连同字母指数不变.
3.合并同类项一定要完全、彻底，不能有漏项，而且合并同类项结果可能是单项式，也可能是多项式.
4.去括号只是改变式子形式，但不改变式子的值，它属于多项式的恒等变形．
5.去括号和添括号是两种相反的变形，因此可以相互检验正误.
1．幂的乘方法则的条件是“幂”的乘方，结论是“底数不变，指数相乘”．这里的“底数不变”是指“幂”的底数“a”不变．例如：(a3)2=a6，其中，“幂”的底数是“a”，而不是“a2”，指数相乘是指“3×2”．
2．同底数幂的乘法和幂的乘方在应用时，不要发生混淆．
3．式子(a+b)2不可以写成a2 +b2，因为括号内的a与b是“加”的关系，不是“乘”的关系．
4．应用积的乘方时，特别注意观察底数含有几个因式都分别乘方；要特别注意系数及系数符号，对于系数是负数的要多加注意.
整式的混合运算的运算顺序：先乘方，再乘除，后加减，有括号时先算括号里面的.
完全平方公式的几何背景
1.意义：运用几何图形直观理解、解决完全平方公式的推导过程，通过几何图形之间的数量关系对完全平方公式做出几何解释．
2. 常见验证完全平方公式的几何图形
结论：（a+b）2＝a2+2ab+b2．（用大正方形的面积等于边长为a和边长为b的两个正方形与两个长宽分别是a，b的长方形的面积和作为相等关系）
平方差公式的几何背景
1.意义：运用几何图形直观理解、解决平方差公式的推导过程，通过几何图形之间的数量关系对平方差公式做出几何解释．
2. 常见验证平方差公式的几何图形
结论：(a＋b)(a－b)＝a2－b2
题型01 判断同类项
【例1】（2022·湖南湘潭·中考真题）下列整式与ab2为同类项的是（ ）
A．a2bB．-2ab2C．abD．
【变式1-1】（2023·浙江绍兴·一模）下列每组中的两个代数式，属于同类项的是（ ）
A．7a2b和3ab2B．37x2y和-2x2yC．x2yz和x2yD．3x2和3y2
题型02 合并同类项
【例2】（2023·四川自贡·中考真题）计算： ．
【变式2-1】（2022·山东淄博·中考真题）计算的结果是（ ）
A．﹣7a6b2B．﹣5a6b2C．a6b2D．7a6b2
题型03 添（去）括号
【例3】（2023·河北衡水·校考模拟预测）关于-a-b进行的变形或运算：①-a-b=-a+b；②-a-b2=a+b2；③-a-b=a-b；④-a-b3=-a-b3．
其中不正确的是（ ）
A．①②B．③④C．①③D．②④
【变式3-1】（2022·河北邯郸·校联考三模）等号左右两边一定相等的一组是（ ）
A．-a+b=-a+b B．a3=a+a+a
C．-2a+b=-2a-2bD．-a-b=-a-b
题型04 整式的加减
【例4】（2022·西藏·中考真题）下列计算正确的是（ ）
A．2ab﹣ab＝abB．2ab+ab＝2a2b2
C．4a3b2﹣2a＝2a2bD．﹣2ab2﹣a2b＝﹣3a2b2
【变式4-1】（2022·浙江杭州·校考二模）化简（2a﹣b）﹣（2a+b）的结果为（ ）
A．2bB．﹣2bC．4aD．-4a
【变式4-2】（2023·浙江金华·一模）如图是一道关于整式运算的例题及正确的解答过程，其中A，B是两个关于x的二项式．
(1)二项式A为________，二项式B为________．
(2)当x为何值时，A与B的值相等？
【变式4-3】（2022·河北保定·一模）已知：整式A=(2x-3)+(3x+5)．
(1)化简整式A；
(2)若2A+B=5x+6，
①求整式B；
②在“”的“□”内，填入“+，-，×，÷”中的一个运算符号，经过计算发现，结果是不含一次项的整式，请你写出一个符合要求的算式，并计算出结果．

整式的加减运算的实质就是合并同类项.主要的理论依据是：去括号法则，合并同类项法则，以及分配率.因此关于整式加减的一般步骤为：①列出代数式；②去括号；③找出同类项；④合并同类项.需要注意的是整式加减的最后结果中：①不能含有同类项，要合并到不能再合并为止；
②不能出现带分数，带分数要化成假分数.
涉及整式加减运算的常见题型还有代数式求值，这类题目的一般步骤：①代数式化简；②代入计算；③对于某些特殊的代数式，可采用“整体代入”进行计算.做题时特别要注意的是在整式的加减运算过程中，不多项，不漏项，交换项的位置时，要注意连同符号一起交换.
题型05 整式加减的应用
【例5】（2022·内蒙古包头·中考真题）若一个多项式加上3xy+2y2-8，结果得2xy+3y2-5，则这个多项式为 ．
【变式5-1】（2023·湖南长沙·校考三模）已知有2个完全相同的边长为a、b的小长方形和1个边长为m、n的大长方形，小明把这2个小长方形按如图所示放置在大长方形中，小明经过推事得知，要求出图中阴影部分的周长之和，只需知道a、b、m、n中的一个量即可，则要知道的那个量是（ ）
A．aB．bC．mD．n
【变式5-2】（2023·河北邯郸·二模）如图，两个三角形的面积分别是6和4，对应阴影部分的面积分别是m和n，则m﹣n等于（ ）
A．2B．3C．4D．5
【变式5-3】（2023·四川德阳·中考真题）在初中数学文化节游园活动中，被称为“数学小王子”的王小明参加了“智取九宫格”游戏比赛，活动规则是：在九宫格中，除了已经填写的三个数之外的每一个方格中，填入一个数，使每一横行、每一竖列以及两条对角线上的3个数之和分别相等，且均为m．王小明抽取到的题目如图所示，他运用初中所学的数学知识，很快就完成了这个游戏，则m= ．
【变式5-4】（2022·四川乐山·中考真题）如果一个矩形内部能用一些正方形铺满，既不重叠，又无缝隙，就称它为“优美矩形”，如图所示，“优美矩形”ABCD的周长为26，则正方形d的边长为 ．
【变式5-5】（2022·浙江金华·中考真题）如图1，将长为2a+3，宽为2a的矩形分割成四个全等的直角三角形，拼成“赵爽弦图”（如图2），得到大小两个正方形．
(1)用关于a的代数式表示图2中小正方形的边长．
(2)当a=3时，该小正方形的面积是多少？
【变式5-6】（2023·江苏盐城·景山中学校考三模）三角形的一边长为2a+b，第二边比第一边长a+2b，第三边长为3a+3b．
(1)用代数式表示三角形的周长；
(2)当a=3，b=2时，求三角形的周长．
题型06 幂的基本运算
【例6】（2023·安徽·中考真题）下列计算正确的是（ ）
A．a4+a4=a8B．a4⋅a4=a16C．a44=a16D．
【变式6-1】（2023·湖北武汉·中考真题）计算2a23的结果是（ ）
A．B．C．D．8a6
【变式6-2】（2023·黑龙江绥化·中考真题）下列计算中，结果正确的是（ ）
A．(-pq)3=p3q3B．x⋅x3+x2⋅x2=x8
C．25=±5D．a23=a6
【变式6-3】（2023·湖南·中考真题）计算12x32的结果正确的是（ ）
A．x6B．14x6C．D．
【变式6-4】（2023·江苏泰州·中考真题）若a≠0，下列计算正确的是（ ）
A．(-a)0=1B．a6÷a3=a2C．a-1=-aD．
【变式6-5】（2023·内蒙古·中考真题）下列各式计算结果为a5的是（ ）
A．a32B．a10÷a2C．D．
题型07 幂的逆向运算
【例7】（2023·四川德阳·中考真题）已知3x=y，则3x+1=（ ）
A．yB．1+yC．3+yD．3y
【变式7-1】（2023·江苏镇江·中考真题）如图，在甲、乙、丙三只袋中分别装有球29个、29个、5个，先从甲袋中取出2x个球放入乙袋，再从乙袋中取出(2x+2y)个球放入丙袋，最后从丙袋中取出2y个球放入甲袋，此时三只袋中球的个数相同，则2x+y的值等于（ ）

A．128B．64C．32D．16
【变式7-2】（2023·湖南湘潭·模拟预测）若3m=4，9n=7，则3m-2n= ．
【变式7-3】（2023·河北·模拟预测）若43x=2021,47y=2021，则代数式xy与x+y之间关系是 ．
【变式7-4】（2023·河南焦作·一模）已知2x=8，则2x-3的值为 ．
题型08 幂的混合运算
【例8】（2023·浙江温州·中考真题）化简a4⋅(-a)3的结果是（ ）
A．a12B．C．D．-a7
【变式8-1】（2023·湖南常德·校考一模）计算：x23⋅x-3=（ ）
A．B．x3C．D．-x18
【变式8-2】（2023·湖北襄阳·模拟预测）a32÷a⋅a3+a2= ．

幂的运算首先要熟练掌握幂的四条基本性质，要做到不但会直接套用公式，还要能逆用. 其次要注意要求的代数式与已知条件的联系，没明显关系时常常逆用公式将其分解. 第三幂的底数是常数且指数中有常数也有未知数时，通常把常数的整数指数幂化成常数作为其它幂的系数，然后进行其它运算（例：已知22x+3－22x+1=48，求x的值）. 第四底数不同而指数可变相同的，可通过比较底数确定其大小关系，还可通过积的乘方的逆运算相乘.
题型09 整式的乘法
【例9】（2023·陕西·中考真题）计算：（ ）
A．3x4y5B．-3x4y5C．3x3y6D．-3x3y6
【变式9-1】（2022·陕西西安·校考三模）计算：（3m﹣1）（m+5）．
【变式9-2】（2022·重庆·校联考一模）计算题
(1)3ab2-2ab⋅ab
(2)x-2yx2-xy+4y2

当我们遇到多项式与多项式相乘或者是单项式与单项式相乘时，字母前的系数可以先进行相乘，然后再把相同的字母进行相乘，这样分类不容易出错，也能提高大家的计算效率.
题型10 整式的除法
【例10】（2023·江苏扬州·中考真题）若，则括号内应填的单项式是( )
A．aB．2aC．abD．2ab
【变式10-1】（2023·山东青岛·中考真题）计算：8x3y÷2x2= ．
【变式10-2】（2023·北京·模拟预测）计算：4x4-x3+23x2÷-2x2．
【变式10-3】（2022·吉林·中考真题）下面是一道例题及其解答过程的一部分，其中A是关于m的多项式．请写出多项式A，并将该例题的解答过程补充完整．
题型11 利用乘法公式计算
【例11】（2023·甘肃兰州·中考真题）计算：x+2yx-2y-y3-4y．
【变式11-1】（2023·青海西宁·中考真题）计算：(2a-3)2-(a+5)(a-5)．
【变式11-2】（2023·天津·中考真题）计算的结果为 ．
【变式11-3】（2023·江西·中考真题）计算：（a+1）2﹣a2= ．

1.应用完全平方公式计算时，应注意以下几个问题：
①公式中的a，b可是单项式，也可以是多项式；
②对形如两数和（或差）的平方的计算，都可以用这个公式；
③对于三项的可以把其中的两项看做一项后，也可以用完全平方公式．
2.应用平方差公式计算时，应注意以下几个问题：
①左边是两个二项式相乘，并且这两个二项式中有一项完全相同，另一项互为相反数；
②右边是相同项的平方减去相反项的平方；
③公式中的a和b可以是具体数，也可以是单项式或多项式；
④对形如两数和与这两数差相乘的算式，都可以运用这个公式计算，且会比用多项式乘以多项式法则简便．
题型12 通过对完全平方公式变形求值
【例12】（2022·山东滨州·中考真题）若m+n=10，mn=5，则的值为 ．
【变式12-1】（2022·四川德阳·中考真题）已知（x+y）2=25，（x﹣y）2=9，则xy= ．
【变式12-2】（2023·广东云浮·一模）若a+b=3，，则ab等于（ ）
A．2B．1C．﹣2D．﹣1
【变式12-3】（2022·湖北荆门·中考真题）已知x+1x＝3，求下列各式的值：
(1)（x﹣1x）2；(2)x4+1x4．

乘法公式求值类的题目，关键在于恒等变形，反复利用平方差公式和完全平方公式，结合公式中各项的情况，做出相应的变形.
题型13 乘法公式的几何验证
【例13】（2023·四川攀枝花·中考真题）我们可以利用图形中的面积关系来解释很多代数恒等式．给出以下4组图形及相应的代数恒等式：
①a+b2=a2+2ab+b2 ②a-b2=a2-2ab+b2

③ ④(a-b)2=(a+b)2-4ab
其中，图形的面积关系能正确解释相应的代数恒等式的有（ ）
A．1个B．2个C．3个D．4个
【变式13-1】（2022·贵州六盘水·中考真题）如图，学校劳动实践基地有两块边长分别为a，b的正方形秧田A，B，其中不能使用的面积为M．
(1)用含a，M的代数式表示A中能使用的面积___________；
(2)若，a-b=5，求A比B多出的使用面积．
【变式13-2】（2022·湖北随州·中考真题）《几何原本》是古希腊数学家欧几里得的一部不朽著作，是数学发展史的一个里程碑．在该书的第2幕“几何与代数”部分，记载了很多利用几何图形来论证的代数结论，利用几何给人以强烈印象将抽象的逻辑规律体现在具体的图形之中．
(1)我们在学习许多代数公式时，可以用几何图形来推理，观察下列图形，找出可以推出的代数公式，（下面各图形均满足推导各公式的条件，只需填写对应公式的序号）
公式①：a+b+cd=ad+bd+cd
公式②：a+bc+d=ac+ad+bc+bd
公式③：a-b2=a2-2ab+b2
公式④：a+b2=a2+2ab+b2
图1对应公式______，图2对应公式______，图3对应公式______，图4对应公式______；
(2)《几何原本》中记载了一种利用几何图形证明平方差公式a+ba-b=a2-b2的方法，如图5，请写出证明过程；（已知图中各四边形均为矩形）
(3)如图6，在等腰直角三角形ABC中，∠BAC=90°，D为BC的中点，E为边AC上任意一点（不与端点重合），过点E作EG⊥BC于点G，作EH⊥ADF点H过点B作BF//AC交EG的延长线于点F．记△BFG与△CEG的面积之和为S1，△ABD与△AEH的面积之和为．
①若E为边AC的中点，则S1S2的值为_______；
②若E不为边AC的中点时，试问①中的结论是否仍成立？若成立，写出证明过程；若不成立，请说明理由．

思路：利用求面积的两种方法（公式法与补割法），列式（公式法求面积=补割法求面积），化简求解.
考点四 整式化简求值（高频考点）
1.直接代入法：把已知字母的值直接代入代数式计算求值.
2.间接代入法：将已知的代数式化简后，再将已知字母的值代入化简后的代数式中计算求值.
3.整体代入法：①观察已知代数式和所求代数式的关系.
②利用提公因式法、平方差公式、完全平方公式将已知代数式和所求代数式进行变形，使它们成倍分关系.
③把已知代数式看成一个整式代入所求代数式中计算求值．
4.赋值求值法：指代数式中的字母的取值由答题者自己确定，然后求出所提供的代数式的值的一种方法．这是一种开放型题目，答案不唯一.在赋值时，要注意取值范围，选择合适的代数式的值．
5.隐含条件求值法：先通过隐含条件求出字母值，然后化简再求值．
例如：①若几个非负数的和为0，则每个非负数的值均为0
②已知两个单项式为同类项，通过求次数中未知数的值，进而带入到代数式中计算求值.
6.利用“无关”求值：
①若一个代数式的值与某个字母的取值无关时需先对原式进行化简，则可得出该无关字母的系数为0；
②若给定字母写错得出正确答案，则该代数式的值与该字母无关．
7.配方法：若已知条件含有完全平方式，则可通过配方，把条件转化成几个平方和的形式，再利用非负数的性质来确定字母的值，从而求得结果．
8.平方法：在直接求值比较困难时，有时也可先求出其平方，再求平方值的平方根，但要注意最后结果的符号．
9.特殊值法：有些试题，用常规方法直接求解比较困难，若根据答案中所提供的信息，选择某些特殊情况进行分析，或选择某些特殊值进行计算，把一般形式变为特殊形式进行判断，这时常常会使题目变得十分简单．
10.设参法：遇到比值的情况，可对比值整体设参数，把每个字母用参数表示，然后代入计算即可．
11.利用根与系数的关系求解：如果代数式可以看作某两个“字母”的轮换对称式，而这两个“字母”又可能看作某个一元二次方程的根，可以先用根与系数的关系求得其和、积式，再整体代入求值．
12. 利用消元法求值：若已知条件以比值的形式出现，则可利用比例的性质设比值为一个参数，或利用一个字母来表示另一个字母．
13. 利用倒数法求值：将已知条件或待求的代数式作倒数变形，从而求出代数式的值．
题型01 整式化简-直接代入法
【例1】（2022·广西梧州·中考真题）若x=1，则3x-2= ．
【变式1-1】已知a是最小的正整数，b是绝对值最小的有理数，c在数轴上对应的点到原点的距离是6，求的值．
题型02 整式化简-间接代入法
【例2】（2022·山东济宁·中考真题）已知a=2+5，b=2-5，求代数式a2b+ab2 的值．
【变式2-1】（2023·湖南·中考真题）先化简，再求值：，其中a=-3,b=13．
【变式2-2】（2021·广西河池·中考真题）先化简，再求值：(x+1)2-x(x+1)，其中x=2021．
题型03 整式化简-整体代入法
【例3】（2023·山东枣庄·中考真题）若x=3是关x的方程ax2-bx=6的解，则2023-6a+2b的值为 ．
【变式3-1】（2023·湖北十堰·中考真题）若x+y=3，y=2，则x2y+xy2的值是 ．
【变式3-2】（2023·四川成都·中考真题）若3ab-3b2-2=0，则代数式1-2ab-b2a2÷a-ba2b，的值为 ．
【变式3-3】（2023·四川凉山·中考真题）已知x2-2x-1=0，则的值等于 ．
题型04 整式化简-赋值法
【例4】（2023·广东江门·一模）化简：，若x是-1≤x≤2的整数，请选择一个合适的数求代数式的值．
【变式4-1】（2022·江苏苏州·校考模拟预测）先化简，再求值：
（1）（a2b﹣2ab2﹣b3）÷b﹣（a+b）（a﹣b），其中a＝1，b＝﹣2．
（2）先化简（1+2x-3）÷，再从﹣1，0，1，2，3中选取一个合适的数作为x的值代入求值．
题型05 整式化简-隐含条件求值
【例5】（2023·湖南衡阳·校联考二模）已知单项式2a4b-2m+7与3a2mbn+2是同类项，则m+n= ．
【变式5-1】（2022·四川绵阳·校联考一模）若多项式xy|m-n|+(n-2)x2y2+1是关于x，y的三次多项式，则mn= ．
【变式5-2】若7的整数部分是a，的小数部分是b，求ab+5b的值．
【变式5-3】（2023·四川成都·一模）若a-2022+b+2022=2，其中a，b均为整数，则a+b= ．
题型06 整式化简-利用“无关”求值
【例6】若(x2+mx+n)(x2-3x+1)的展开式中不含和x3项，求：(1)m、n 的值．
(2)求(m+n)(m2-mn+n2)的值．
【变式6-1】已知多项式M=x2+5x-a，N=-x+2，P=x3+3x2+5，且M·N+P的值与x的取值无关，求字母a的值．
【变式6-2】有这样一道题：计算13x2-3x2+3xy-35y2+83x2+3xy+25y2的值，其中x=-12，y=2．甲同学把“x=-12”错抄成了“x=12”，他的计算结果也是正确的，你知道这是怎么回事吗？
题型07 整式化简-配方法
【例7】已知a2＋b2＋2a－4b＋5＝0，求2a2＋4b－3的值．
【变式7-1】已知x2-2x+y2+8y+17=0，求(x+y)2的值．
题型08 整式化简-平方法
【例8】（2023·云南昆明·云南师范大学实验中学校考模拟预测）已知x+1x=6，则x2+1x2=（ ）
A．38B．36C．34D．32
【变式8-1】已知x+y=7且xy=12，则当x题型09 整式化简-特殊值法
【例9】若(2-x)3=a0+a1x+a2x2+a3x3，则a0+a22-a1+a32的值为 ．
【变式9-1】已知实数a，b满足a⋅b=1，那么1a2+1+1b2+1的值为（ ）
A．14B．12C．1D．2
题型10 整式化简-设参法
【例10】（2023·广东湛江·校考一模）已知a2=b3=c4≠0,则a+bc的值为( )
A．45B．54C．2D．12
【变式10-1】（2023·上海·一模）已知ab=23，那么代数式b-aa+b的值是 ．
题型11 整式化简-利用根与系数关系求值
【例11】（2023·江西九江·校考一模）已知a，b是一元二次方程x2-2x-1=0的两个实数根，则a+b+ab的值为 ．
【变式11-1】（2023·河北衡水·三模）已知x1，x2是关于x的方程的两实数根，且x1+x2=-2，x1⋅x2=1，则a的值为 ，ba的值是 ．
【变式11-2】（2023·云南临沧·三模）已知一元二次方程x2-5x-6=0的两根分别为a，b，则1a+1b的值为（ ）
A．-16B．16C．56D．-56
题型12 整式化简-消元法求值
【例12】如果ab=2，则a2-ab+b2a2+b2= ( )
A．45B．1C．35D．2
【变式12-1】若a+2b=9c，a-2b=5c，则2a2+3b2+7c2a2-4b2+9c2= ．
题型13 整式化简-倒数法求值
【例13】若22y2+3y+7的值为14，则14y2+6y-1的值为( )．
A．1B．－1C．-17D．15
【变式13-1】已知xx2+1=13，求x2x4+1的值．
考点五 因式分解
1.因式分解分解对象是多项式，分解结果必须是积的形式，且积的因式必须是整式，这三个要素缺一不可；
2.因式分解必须是恒等变形；
3.因式分解必须分解到每个因式都不能分解为止.
4.因式分解与整式乘法是互逆变形，因式分解是把和差化为积的形式，而整式乘法是把积化为和差的形式．
题型01 判断因式分解
【例1】（2023·山东·中考真题）下列各式从左到右的变形，因式分解正确的是（ ）
A．(a+3)2=a2+6a+9B．a2-4a+4=aa-4+4
C．D．
【变式1-1】（2022·湖南永州·中考真题）下列因式分解正确的是（ ）
A．ax+ay=ax+y+1B．3a+3b=3a+b
C．a2+4a+4=a+42D．a2+b=aa+b
题型02 选用合适的方法因式分解
【例2】（2023·河北·中考真题）若k为任意整数，则的值总能（ ）
A．被2整除B．被3整除C．被5整除D．被7整除
【变式2-1】（2023·黑龙江绥化·中考真题）因式分解：x2+xy-xz-yz= ．
【变式2-2】（2023·湖北黄石·中考真题）因式分解：xy-1+41-y= ．
【变式2-3】（2022·四川内江·中考真题）分解因式：a4﹣3a2﹣4＝ ．
【变式2-4】（2023·安徽芜湖·芜湖市第二十九中学校考二模）因式分解：4x2-y2+2y-1= ．

因式分解的关键在于熟练掌握因式分解的两种基本方法：提取公因式法和公式法．因式分解的一般步骤：
题型03 与因式分解有关的探究题
【例3】（2023·河北石家庄·二模）嘉淇上小学时得知“一个数的各个数字之和能被3整除，那么这个数就能被3整除”，她后来做了如下提示：
(1)通过计算验证258能否被3整除；
(2)用嘉淇的方法证明4374能被3整除；
(3)设abcd是一个四位数．a，b，c，d分别为对应数位上的数字，请论证“若a+b+c+d能被3整除，则这个数可以被3整除”．
【变式3-1】（2023·河北衡水·二模）发现两个相邻奇数中，较大奇数与较小奇数的平方差一定是8的倍数．
验证计算52-32的值，并求这个值是8的几倍．
探究设“发现”中较小的奇数为2n+1,请论证“发现”中的结论正确．
【变式3-2】（2023·河北张家口·校考模拟预测）问题情景：将下列完全平方式进行因式分解，将结果直接写在横线上．
x2+2x+1=(x+1)2；4x2-4x+1=(2x-1)2；9x2-30x+25=__________；
探究发现：观察以上多项式，发现：22=4×1×1；(-4)2=4×4×1；(-30)2=4×9×25；
归纳猜想：若多项式ax2+bx+c(a>0,c>0)是完全平方式，则a，b，c之间存在的数量关系为；
验证结论：嘉琪验证归纳猜想中的结论的过程如下，请补全嘉琪的验证过程；
ax2+bx+c(a>0,c>0)
=ax2+bax+c
=a(x+__________)2+__________
∵ax2+bx+c是完全平方式，
∴__________，即．
解决问题：
①若多项式(n+1)x2-(2n+6)x+(n+6)是一个完全平方式，求n的值；
②若多项式9y2+4加上一个含字母y的单项式就能变形为一个完全平方式，请直接写出所有满足条件的单项式．
【变式3-3】（2023·河北石家庄·三模）【提出问题】在数学课上，老师提出一个问题：“任意奇数的平方减去1后都一定是8的倍数吗？”
（1）【解决问题】计算：32-1=______；52-1=______；72-1=______；以上计算结果均______（填“是”或“不是”）8的倍数；
（2）设奇数为2n+1（n为整数），请你先试着回答老师提出的问题，再“论证”你的结论；
（3）【拓展延伸】任意奇数的平方加上1后都一定是______的倍数．
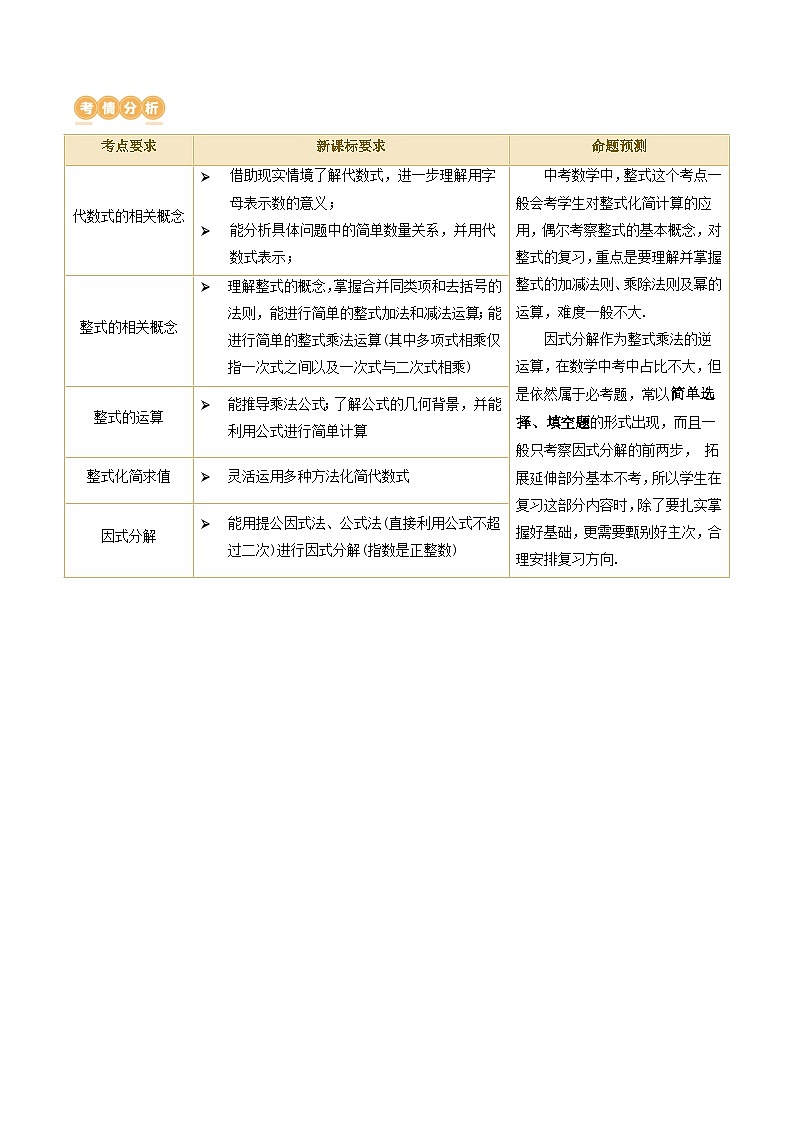
考点要求
新课标要求
命题预测
代数式的相关概念
借助现实情境了解代数式，进一步理解用字母表示数的意义；
能分析具体问题中的简单数量关系，并用代数式表示；
中考数学中，整式这个考点一般会考学生对整式化简计算的应用，偶尔考察整式的基本概念，对整式的复习，重点是要理解并掌握整式的加减法则、乘除法则及幂的运算，难度一般不大.
因式分解作为整式乘法的逆运算，在数学中考中占比不大，但是依然属于必考题，常以简单选择、填空题的形式出现，而且一般只考察因式分解的前两步， 拓展延伸部分基本不考，所以学生在复习这部分内容时，除了要扎实掌握好基础，更需要甄别好主次，合理安排复习方向.
整式的相关概念
理解整式的概念，掌握合并同类项和去括号的法则，能进行简单的整式加法和减法运算；能进行简单的整式乘法运算(其中多项式相乘仅指一次式之间以及一次式与二次式相乘)
整式的运算
能推导乘法公式；了解公式的几何背景，并能利用公式进行简单计算
整式化简求值
灵活运用多种方法化简代数式
因式分解
能用提公因式法、公式法(直接利用公式不超过二次)进行因式分解(指数是正整数)

判断依据
次数
系数与项数
整式
单项式
①数字与字母或字母与字母相乘组成的代数式 ②单独的一个数或字母
所有字母指数的和
系数：单项式中不为零的数字因数
多项式
几个单项式的和
次数最高项的次数
项数：多项式中所含单项式的个数
整式的
加减
同类项
所含字母相同，并且相同字母的指数也相同的项叫做同类项.
合并同类项
把同类项中的系数相加减，字母与字母的指数不变.
添（去）括号法则
括号外是“+”，添(去) 括号不变号，
括号外是“-”，添(去) 括号都变号.
整式的加减法则
几个整式相加减，如有括号就先去括号，然后再合并同类项.
整式的乘除
运算步骤说明
补充说明及注意事项
单项式乘单项式
①将单项式系数相乘作为积的系数;
②相同字母的因式，利用同底数幂的乘法，作为积的一个因式;
③单独出现的字母，连同它的指数，作为积的一个因式.
1）实质:乘法的交换律和同底数幂的乘法法则的综合应用.
2）单项式乘单项式所得结果仍是单项式 .
单项式乘多项式
①先用单项式和多项式的每一项分别相乘；
②再把所得的积相加.
1）单项式乘多项式实质上是转化为单项式乘以单项式
2）单项式乘多项式的结果是多项式，积的项数与原多项式的项数相同.
多项式乘多项式
①先用一个多项式的每一项与另一个多项式的每一项相乘，
②再把所得的积相加．
运用法则时应注意以下两点：
①相乘时，按一定的顺序进行，必须做到不重不漏；
②多项式与多项式相乘，多项式的每一项都应该带上它前面的正负号.且结果仍是多项式，在合并同类项之前，积的项数应等于原多项式的项数之积．
单项式除单项式
①将单项式系数相除作为商的系数；
②相同字母的因式，利用同底数幂的除法，作为商的一个因式；
③只在被除式里含有的字母连同指数不变.

多项式除单项式
①先把这个多项式的每一项除以这个单项式；
②再把所得的商相加

【例题】先去括号，再合并同类项：2A-3B
解：原式=4x-6-9x-15=________________
16
7
4
例先去括号，再合并同类项：m（A）-6(m+1)．
解：m（A）-6(m+1)=m2+6m-6m-6= ．
嘉淇的提示：
258=2×100+5×10+8=2×99+1+5×9+1+8
=2×99+2+5×9+5+8=2×99+5×9+2+5+8
=32×33+5×3+3×5
∵2×33+5×3为整数，5为整数，
∴32×33+5×3能被3整除，3×5能被3整除，∴258能被3整除．