



所属成套资源:2025年中考数学一轮复习讲与 考点精析+真题精讲+题型突破+专题精练(2份,原卷版+解析版)
- 2025年中考数学一轮复习讲与练第四章第三讲 特殊三角形及其性质(含解直角三角形)(考点精析+真题精讲)(2份,原卷版+解析版) 试卷 0 次下载
- 2025年中考数学一轮复习讲与练第四章第三讲 特殊三角形及其性质(含解直角三角形)(题型突破+专题精练)(2份,原卷版+解析版) 试卷 0 次下载
- 2025年中考数学一轮复习讲与练第四章第四讲 全等、相似三角形(题型突破+专题精练)(2份,原卷版+解析版) 试卷 0 次下载
- 2025年中考数学一轮复习讲与练第四章第五讲 几何测量问题(考点精析+真题精讲)(2份,原卷版+解析版) 试卷 0 次下载
- 2025年中考数学一轮复习讲与练第四章第五讲 几何测量问题(题型突破+专题精练)(2份,原卷版+解析版) 试卷 0 次下载
2025年中考数学一轮复习讲与练第四章第四讲 全等、相似三角形(考点精析+真题精讲)(2份,原卷版+解析版)
展开
这是一份2025年中考数学一轮复习讲与练第四章第四讲 全等、相似三角形(考点精析+真题精讲)(2份,原卷版+解析版),文件包含2025年中考数学一轮复习讲与练第4章第四讲全等相似三角形考点精析+真题精讲原卷版docx、2025年中考数学一轮复习讲与练第4章第四讲全等相似三角形考点精析+真题精讲解析版docx等2份试卷配套教学资源,其中试卷共37页, 欢迎下载使用。
第4讲全等、相似三角形
→➊考点精析←
→➋真题精讲←
考向一全等三角形
考向二相似三角形
第4讲全等、相似三角形
→➊考点精析←
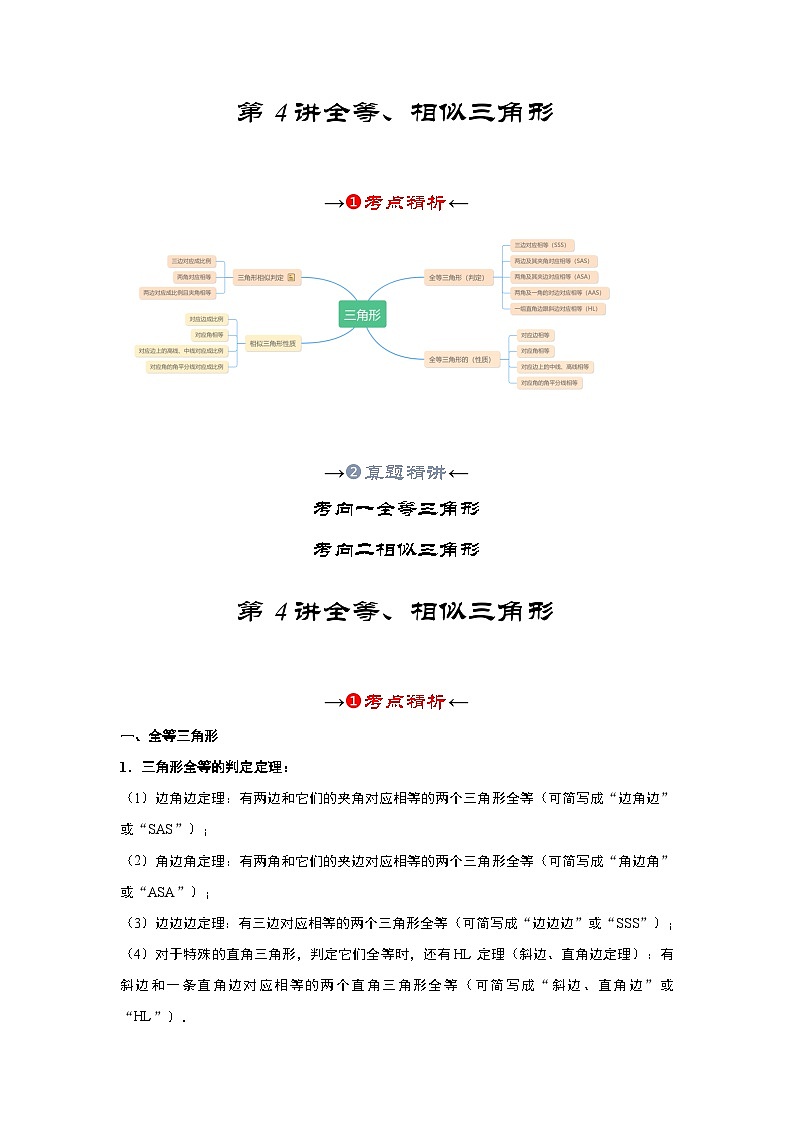
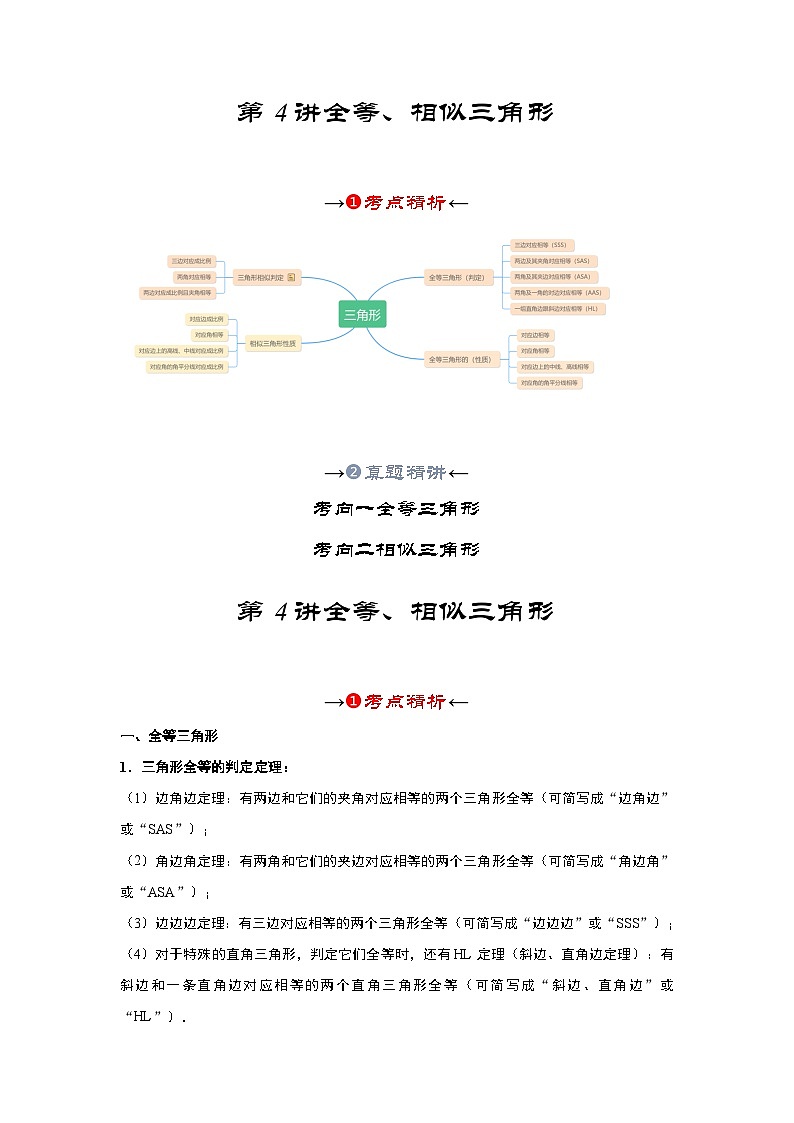
一、全等三角形
1.三角形全等的判定定理:
(1)边角边定理:有两边和它们的夹角对应相等的两个三角形全等(可简写成“边角边”或“SAS”);
(2)角边角定理:有两角和它们的夹边对应相等的两个三角形全等(可简写成“角边角”或“ASA”);
(3)边边边定理:有三边对应相等的两个三角形全等(可简写成“边边边”或“SSS”);
(4)对于特殊的直角三角形,判定它们全等时,还有HL定理(斜边、直角边定理):有斜边和一条直角边对应相等的两个直角三角形全等(可简写成“斜边、直角边”或“HL”).
2.全等三角形的性质:
(1)全等三角形的对应边相等,对应角相等;
(2)全等三角形的周长相等,面积相等;
(3)全等三角形对应的中线、高线、角平分线、中位线都相等.
二、相似三角形的判定及性质
1.定义
对应角相等,对应边成比例的两个三角形叫做相似三角形,相似三角形对应边的比叫做相似比.
2.性质
(1)相似三角形的对应角相等;
(2)相似三角形的对应线段(边、高、中线、角平分线)成比例;
(3)相似三角形的周长比等于相似比,面积比等于相似比的平方.
3.判定
(1)有两角对应相等,两三角形相似;
(2)两边对应成比例且夹角相等,两三角形相似;
(3)三边对应成比例,两三角形相似;
(4)两直角三角形的斜边和一条直角边对应成比例,两直角三角形相似.
【方法技巧】判定三角形相似的几条思路:
(1)条件中若有平行线,可采用相似三角形的判定(1);
(2)条件中若有一对等角,可再找一对等角[用判定(1)]或再找夹边成比例[用判定(2)];
(3)条件中若有两边对应成比例,可找夹角相等;
(4)条件中若有一对直角,可考虑再找一对等角或证明斜边、直角边对应成比例;
(5)条件中若有等腰条件,可找顶角相等,或找一个底角相等,也可找底和腰对应成比例.
→➋真题精讲←
题型一全等三角形
1.(2023·云南·统考中考真题)如图,两点被池塘隔开,三点不共线.设的中点分别为.若米,则( )
A.4米B.6米C.8米D.10米
【答案】B
【分析】根据三角形中位线定理计算即可.
【详解】解∶∵的中点分别为,
∴是的中位线,
∴米,
故选:B.
【点睛】本题考查的是三角形中位线定理,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.
2.(2023·浙江台州·统考中考真题)如图,锐角三角形中,,点D,E分别在边,上,连接,.下列命题中,假命题是( ).
A.若,则B.若,则
C.若,则D.若,则
【答案】A
【分析】由,可得,再由,由无法证明与全等,从而无法得到;证明可得;证明,可得,即可证明;证明,即可得出结论.
【详解】解:∵,
∴,
∵若,
又,
∴与满足“”的关系,无法证明全等,
因此无法得出,故A是假命题,
∵若,
∴,
在和中,
,
∴,
∴,故B是真命题;
若,则,
在和中,
,
∴,
∴,
∵,
∴,故C是真命题;
若,则在和中,
,
∴,
∴,故D是真命题;
故选:A.
【点睛】本题考查等腰三角形的判定和性质,全等三角形的判定和性质,命题的真假判断,正确的命题叫真命题,错误的命题叫假命题,判断命题的真假关键是掌握相关性质定理.
3.(2023·河北·统考中考真题)在和中,.已知,则( )
A.B.C.或D.或
【答案】C
【分析】过A作于点D,过作于点,求得,分两种情况讨论,利用全等三角形的判定和性质即可求解.
【详解】解:过A作于点D,过作于点,
∵,
∴,
当在点D的两侧,在点的两侧时,如图,
∵,,
∴,
∴;
当在点D的两侧,在点的同侧时,如图,
∵,,
∴,
∴,即;
综上,的值为或.
故选:C.
【点睛】本题考查了含30度角的直角三角形的性质,全等三角形的判定和性质,分类讨论是解题的关键.
4.(2023·湖北随州·统考中考真题)如图,在中,,D为AC上一点,若是的角平分线,则___________.
【答案】3
【分析】首先证明,,设,在中,利用勾股定理构建方程即可解决问题.
【详解】解:如图,过点D作的垂线,垂足为P,
在中,∵,
∴,
∵是的角平分线,
∴,
∵,
∴,
∴,,
设,
在中,∵,,
∴,
∴,
∴.
故答案为:3.
【点睛】本题考查了角平分线的性质,全等三角形的判定和性质,勾股定理等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
5.(2023·广东深圳·统考中考真题)如图,在中,,,点D为上一动点,连接,将沿翻折得到,交于点G,,且,则______.
【答案】
【分析】于点M,于点N,则,过点G作于点P,设,根据得出,继而求得,,,再利用,求得,利用勾股定理求得,,故,
【详解】由折叠的性质可知,是的角平分线,,用证明,从而得到,设,则,,利用勾股定理得到即,化简得,从而得出,利用三角形的面积公式得到:.
作于点M,于点N,则,
过点G作于点P,
∵于点M,
∴,
设,则,,
又∵,,
∴,,,
∵,即,
∴,,
在中,,,
设,则
∴
∴,
∵,,,
∴,
∵,,
∴,
∴,
∵,,,,
∴,
∴,
设,则,,
在中,,即,
化简得:,
∴,
∴
故答案是:.
【点睛】本题考查解直角三角形,折叠的性质,全等三角形的判定与性质,角平分线的性质,勾股定理等知识,正确作出辅助线并利用勾股定理列出方程是解题的关键.
6.(2023·云南·统考中考真题)如图,是的中点,.求证:.
【答案】见解析
【分析】根据是的中点,得到,再利用证明两个三角形全等.
【详解】证明:是的中点,
,
在和中,
,
【点睛】本题考查了线段中点,三角形全等的判定,其中对三角形判定条件的确定是解决本题的关键.
7.(2023·四川宜宾·统考中考真题)已知:如图,,,.求证:.
【答案】见解析
【分析】根据平行线的性质得出,然后证明,证明,根据全等三角形的性质即可得证.
【详解】证明:∵,
∴,
∵,
∴
即
在与中
,
∴,
∴.
【点睛】本题考查了全等三角形的性质与判定,熟练掌握全等三角形的性质与判定是解题的关键.
8.(2023·全国·统考中考真题)如图,点C在线段上,在和中,.
求证:.
【答案】证明见解析
【分析】直接利用证明,再根据全等三角形的性质即可证明.
【详解】解:在和中,
∴
∴.
【点睛】本题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定方法是解题的关键.
9.(2023·山东临沂·统考中考真题)如图,.
(1)写出与的数量关系
(2)延长到,使,延长到,使,连接.求证:.
(3)在(2)的条件下,作的平分线,交于点,求证:.
【答案】(1)
(2)见解析
(3)见解析
【分析】(1)勾股定理求得,结合已知条件即可求解;
(2)根据题意画出图形,证明,得出,则,即可得证;
(3)延长交于点,延长交于点,根据角平分线以及平行线的性质证明,进而证明,即可得证.
【详解】(1)解:∵
∴,
∵
∴
即;
(2)证明:如图所示,
∴
∴,
∵,
∴
∵,,
∴
∴
∴
∴
(3)证明:如图所示,延长交于点,延长交于点,
∵,,
∴,
∴
∵是的角平分线,
∴,
∴
∴
∵,
∴,,
∴,
又∵,
∴,
即,
∴,
又,则,
在中,
,
∴,
∴
【点睛】本题考查了全等三角形的与判定,等腰三角形的性质与判定,勾股定理,平行线的性质与判定,熟练掌握全等三角形的性质与判定是解题的关键.
10.(2023·山东聊城·统考中考真题)如图,在四边形中,点E是边上一点,且,.
(1)求证:;
(2)若,时,求的面积.
【答案】(1)见解析
(2)
【分析】(1)由求出,然后利用证明,可得,再由等边对等角得出结论;
(2)过点E作于F,根据等腰三角形的性质和含直角三角形的性质求出和,然后利用勾股定理求出,再根据三角形面积公式计算即可.
【详解】(1)证明:∵,
∴,即,
∴,
在和中,,
∴,
∴,
∴;
(2)解:过点E作于F,
由(1)知,
∵,
∴,
∵,
∴,
∴,,
∴.
【点睛】本题考查了三角形内角和定理,全等三角形的判定和性质,等腰三角形的性质,含直角三角形的性质以及勾股定理等知识,正确寻找证明三角形全等的条件是解题的关键.
题型二相似三角形
11.(2023·重庆·统考中考真题)如图,已知,,若的长度为6,则的长度为( )
A.4B.9C.12D.
【答案】B
【分析】根据相似三角形的性质即可求出.
【详解】解:∵,
∴,
∵,,
∴,
∴,
故选:B.
【点睛】此题考查的是相似三角形的性质,掌握相似三角形的边长比等于相似比是解决此题的关键.
12.(2023·浙江嘉兴·统考中考真题)如图,在直角坐标系中,的三个顶点分别为,现以原点O为位似中心,在第一象限内作与的位似比为2的位似图形,则顶点的坐标是( )
A.B.C.D.
【答案】C
【分析】直接根据位似图形的性质即可得.
【详解】解:∵的位似比为2的位似图形是,且,
,即,
故选:C.
【点睛】本题考查了坐标与位似图形,熟练掌握位似图形的性质是解题关键.
13.(2023·安徽·统考中考真题)如图,点在正方形的对角线上,于点,连接并延长,交边于点,交边的延长线于点.若,,则( )
A.B.C.D.
【答案】B
【分析】根据平行线分线段成比例得出,根据,得出,则,进而可得,根据,得出,根据相似三角形的性质得出,进而在中,勾股定理即可求解.
【详解】解:∵四边形是正方形,,,
∴,,,
∵,
∴
∴,,
∴,
则,
∴,
∵,
∴,
∴
∴,
在中,,
故选:B.
【点睛】本题考查了正方形的性质,平行线分线段成比例,相似三角形的性质与判定,勾股定理,熟练掌握以上知识是解题的关键.
14.(2023·四川内江·统考中考真题)如图,在中,点D、E为边的三等分点,点F、G在边上,,点H为与的交点.若,则的长为( )
A.1B.C.2D.3
【答案】C
【分析】由三等分点的定义与平行线的性质得出,,,是的中位线,易证,得,解得,则.
【详解】解:、为边的三等分点,,
,,,
,是的中位线,
,
,
,
,即,
解得:,
,
故选:C.
【点睛】本题考查了三等分点的定义、平行线的性质、相似三角形的判定与性质、三角形中位线定理等知识;熟练掌握相似三角形的判定与性质是解题的关键.
15.(2023·内蒙古赤峰·统考中考真题)如图,把一个边长为5的菱形沿着直线折叠,使点C与延长线上的点Q重合.交于点F,交延长线于点E.交于点P,于点M,,则下列结论,①,②,③,④.正确的是( )
A.①②③B.②④C.①③④D.①②③④
【答案】A
【分析】由折叠性质和平行线的性质可得,根据等角对等边即可判断①正确;根据等腰三角形三线合一的性质求出,再求出即可判断②正确;由得,求出即可判断③正确;根据即可判断④错误.
【详解】由折叠性质可知:,
∵,
∴.
∴.
∴.
故正确;
∵,,
∴.
∵,
∴.
故正确;
∵,
∴.
∴.
∵,
∴.
故正确;
∵,
∴.
∴.
∴.
∵,
∴.
∴与不相似.
∴.
∴与不平行.
故错误;
故选:A.
【点睛】本题主要考查了折叠的性质,平行线的性质,等腰三角形的性质,相似三角形的判定和性质,菱形的性质等知识,属于选择压轴题,有一定难度,熟练掌握相关性质是解题的关键.
16.(2023·湖北鄂州·统考中考真题)如图,在平面直角坐标系中,与位似,原点O是位似中心,且.若,则点的坐标是___________.
【答案】
【分析】直接利用位似图形的性质得出相似比进而得出对应线段的长.
【详解】解∶设
∵与位似,原点是位似中心,且.若,
∴位似比为,
∴,
解得,,
∴
故答案为:.
【点睛】此题主要考查了位似变换,正确得出相似比是解题关键.
17.(2023·四川乐山·统考中考真题)如图,在平行四边形中,E是线段上一点,连结交于点F.若,则__________.
【答案】
【分析】四边形是平行四边形,则,可证明,得到,由进一步即可得到答案.
【详解】解:∵四边形是平行四边形,
∴,
∴,
∴,
∴,
∵,
∴,
∴.
故答案为:
【点睛】此题考查了平行四边形的性质、相似三角形的判定和性质等知识,证明是解题的关键.
18.(2023·内蒙古·统考中考真题)如图,在中,,将绕点A逆时针方向旋转,得到.连接,交于点D,则的值为________.
【答案】5
【分析】过点D作于点F,利用勾股定理求得,根据旋转的性质可证、是等腰直角三角形,可得,再由,得,证明,可得,即,再由,求得,从而求得,,即可求解.
【详解】解:过点D作于点F,
∵,,,
∴,
∵将绕点A逆时针方向旋转得到,
∴,,
∴是等腰直角三角形,
∴,
又∵,
∴,
∴是等腰直角三角形,
∴,
∵,即,
∵ ,,
∴,
∴,即,
又∵,
∴,
∴,,
∴,
故答案为:5.
【点睛】本题考查旋转的性质、等腰三角形的判定与性质、相似三角形的判定与性质、三角形的面积,熟练掌握相关知识是解题的关键.
19.(2023·四川泸州·统考中考真题)如图,,是正方形的边的三等分点,是对角线上的动点,当取得最小值时,的值是___________.
【答案】
【分析】作点F关于的对称点,连接交于点,此时取得最小值,过点作的垂线段,交于点K,根据题意可知点落在上,设正方形的边长为,求得的边长,证明,可得,即可解答.
【详解】解:作点F关于的对称点,连接交于点,过点作的垂线段,交于点K,
由题意得:此时落在上,且根据对称的性质,当P点与重合时取得最小值,
设正方形的边长为a,则,
四边形是正方形,
,,
,
,
,
,
,
,
,
,
,
当取得最小值时,的值是为,
故答案为:.
【点睛】本题考查了四边形的最值问题,轴对称的性质,相似三角形的证明与性质,正方形的性质,正确画出辅助线是解题的关键.
20.(2023·湖南·统考中考真题)在中,是斜边上的高.
(1)证明:;
(2)若,求的长.
【答案】(1)见解析
(2)
【分析】(1)根据三角形高的定义得出,根据等角的余角相等,得出,结合公共角,即可得证;
(2)根据(1)的结论,利用相似三角形的性质即可求解.
【详解】(1)证明:∵是斜边上的高.
∴,
∴,
∴
又∵
∴,
(2)∵
∴,
又
∴.
【点睛】本题考查了相似三角形的性质与判定,熟练掌握相似三角形的性质与判定是解题的关键.
21.(2023·四川眉山·统考中考真题)如图,中,点E是的中点,连接并延长交的延长线于点F.
(1)求证:;
(2)点G是线段上一点,满足,交于点H,若,求的长.
【答案】(1)见解析
(2)
【分析】(1)根据平行四边形的性质可得,,证明,推出,即可解答;
(2)通过平行四边形的性质证明,再通过(1)中的结论得到,最后证明,利用对应线段比相等,列方程即可解答.
【详解】(1)证明:四边形是平行四边形,
,,
,
是的中点,
,
,
,
∴,
;
(2)解:四边形是平行四边形,
,,
,,
,
,
,
,
,
,
设,则,
可得方程,
解得,
即的长为.
【点睛】本题考查了平行四边形的性质,等腰三角形的判定和性质,相似三角形的判定和性质,熟练运用上述性质证明三角形相似是解题的关键.
22.(2023·上海·统考中考真题)如图,在梯形中,点F,E分别在线段,上,且,
(1)求证:
(2)若,求证:
【答案】见解析
【分析】(1)先根据平行线的性质可得,再根据三角形的全等的判定可得,然后根据全等的三角形的性质即可得证;
(2)先根据全等三角形的性质可得,从而可得,再根据相似三角形的判定可得,然后根据相似三角形的性质即可得证.
【详解】(1)证明:,
,
在和中,,
,
.
(2)证明:,
,
,即,
在和中,,
,
,
由(1)已证:,
,
.
【点睛】本题考查了三角形全等的判定与性质、相似三角形的判定与性质,熟练掌握相似三角形的判定与性质是解题关键.
相关试卷
这是一份2025年中考数学一轮复习讲与练第四章第六讲 尺规作图(考点精析+真题精讲)(2份,原卷版+解析版),文件包含2025年中考数学一轮复习讲与练第4章第六讲尺规作图考点精析+真题精讲原卷版docx、2025年中考数学一轮复习讲与练第4章第六讲尺规作图考点精析+真题精讲解析版docx等2份试卷配套教学资源,其中试卷共38页, 欢迎下载使用。
这是一份2025年中考数学一轮复习讲与练第四章第五讲 几何测量问题(考点精析+真题精讲)(2份,原卷版+解析版),文件包含2025年中考数学一轮复习讲与练第4章第五讲几何测量问题考点精析+真题精讲原卷版docx、2025年中考数学一轮复习讲与练第4章第五讲几何测量问题考点精析+真题精讲解析版docx等2份试卷配套教学资源,其中试卷共34页, 欢迎下载使用。
这是一份2025年中考数学一轮复习讲与练第四章第一讲 直线与角(考点精析+真题精讲)(2份,原卷版+解析版),文件包含2025年中考数学一轮复习讲与练第4章第一讲直线与角考点精析+真题精讲原卷版docx、2025年中考数学一轮复习讲与练第4章第一讲直线与角考点精析+真题精讲解析版docx等2份试卷配套教学资源,其中试卷共21页, 欢迎下载使用。










