广东省深圳市福田区红岭教育集团2024-2025学年上学期九年级数学期中试卷

这是一份广东省深圳市福田区红岭教育集团2024-2025学年上学期九年级数学期中试卷，共30页。试卷主要包含了斗拱是中国古典建筑上的重要部件等内容，欢迎下载使用。
一．选择题（共8小题）
1．斗拱是中国古典建筑上的重要部件．如图是一种斗形构件“三才升”的示意图及其主视图，则它的左视图为（ ）
A．B．C．D．
2．若关于x的一元二次方程x2﹣4x+c＝0有两个相等的实数根，则实数c的值为（ ）
A．﹣16B．﹣4C．4D．16
3．某区为了解初中生近视情况，在全区进行初中生视力的随机抽查，结果如下表．根据抽测结果，下列对该区初中生近视的概率的估计，最合理的是（ ）
A．0.423B．0.400C．0.413D．0.410
4．如图，在平面直角坐标系中，已知点A（﹣1，2）、B（﹣3，﹣1），以原点O为位似中心，相似比为2，把△ABO放大，则点A的对应点A′的坐标是（ ）
A．（﹣6，﹣2）B．（﹣2，4）
C．（﹣6，﹣2）或（6，2）D．（﹣2，4）或（2，﹣4）
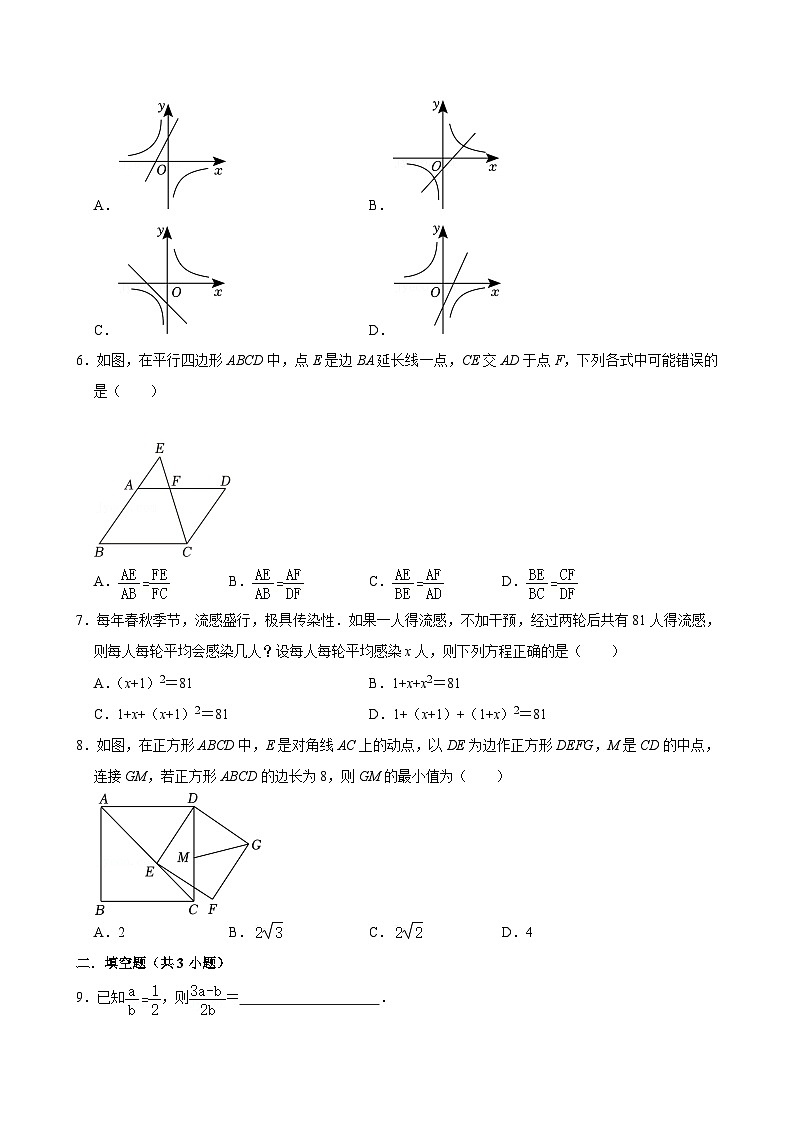
5．在同一平面直角坐标系中，函数y＝﹣kx+k与的大致图象可能为（ ）
A．B．
C．D．
6．如图，在平行四边形ABCD中，点E是边BA延长线一点，CE交AD于点F，下列各式中可能错误的是（ ）
A．B．C．D．
7．每年春秋季节，流感盛行，极具传染性．如果一人得流感，不加干预，经过两轮后共有81人得流感，则每人每轮平均会感染几人？设每人每轮平均感染x人，则下列方程正确的是（ ）
A．（x+1）2＝81B．1+x+x2＝81
C．1+x+（x+1）2＝81D．1+（x+1）+（1+x）2＝81
8．如图，在正方形ABCD中，E是对角线AC上的动点，以DE为边作正方形DEFG，M是CD的中点，连接GM，若正方形ABCD的边长为8，则GM的最小值为（ ）
A．2B．C．D．4
二．填空题（共3小题）
9．已知，则＝ ．
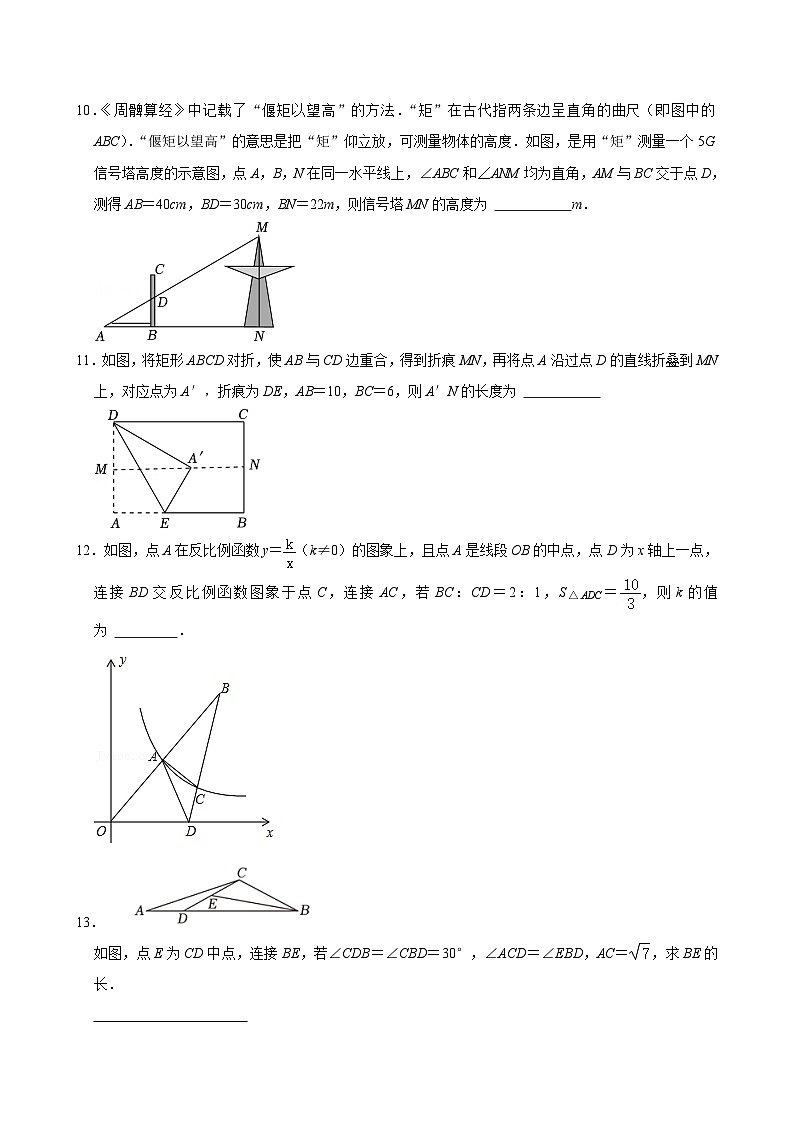
10．《周髀算经》中记载了“偃矩以望高”的方法．“矩”在古代指两条边呈直角的曲尺（即图中的ABC）．“偃矩以望高”的意思是把“矩”仰立放，可测量物体的高度．如图，是用“矩”测量一个5G信号塔高度的示意图，点A，B，N在同一水平线上，∠ABC和∠ANM均为直角，AM与BC交于点D，测得AB＝40cm，BD＝30cm，BN＝22m，则信号塔MN的高度为 m．
11．如图，将矩形ABCD对折，使AB与CD边重合，得到折痕MN，再将点A沿过点D的直线折叠到MN上，对应点为A′，折痕为DE，AB＝10，BC＝6，则A′N的长度为
12．如图，点A在反比例函数y＝（k≠0）的图象上，且点A是线段OB的中点，点D为x轴上一点，连接BD交反比例函数图象于点C，连接AC，若BC：CD＝2：1，S△ADC＝，则k的值为 ．
13．
如图，点E为CD中点，连接BE，若∠CDB＝∠CBD＝30°，∠ACD＝∠EBD，AC＝，求BE的长．

三．解答题（共8小题）
14． 解方程：x2+2x﹣24＝0．
15．2024年10月21日，红岭中学举行了第十三届运动会．本届赛事共设置跳高、跳远、铅球三个项目．赛后随机抽取了部分参赛选手对本次赛事组织进行满意度评分调查，整理后得到下列不完整的图表：
请根据表中提供的信息，解答下列问题：
（1）此次调查共抽取了 名选手，m＝ ，n＝ ；
（2）扇形统计图中，B等级所对应的扇形圆心角度数是 度；
（3）赛后若在三个项目的冠军中随机抽取两人访谈，请用列表或画树状图的方法，求出恰好抽到跳高和跳远冠军的概率．
16．2024年巴黎奥运会顺利闭幕，吉祥物“弗里热”深受奥运迷的喜爱，一商场以20元的进价进一批“弗里热”纪念品，以30元每个的价格售出，每周可以卖出500个，经过市场调查发现，价格每涨5元，就少卖50个．
（1）若商场计划一周的利润达到8000元，并且更大优惠让利消费者，售价应定为多少钱？
（2）因商场改变销售策略，在不改变（1）的销售价格基础上，销售量稳步提升，两周后销售量达到了484个，求这两周的平均增长率．
17．如图，在菱形ABCD中，对角线AC，BD相交于点O，延长CB到点E，使得BE＝BC．连接AE．过点B作BF∥AC，交AE于点F，连接OF．
（1）求证：四边形AFBO是矩形；
（2）若∠E＝30°，OF＝2，求菱形ABCD的面积．
18．如果关于x的一元二次方程ax2+bx+c＝0（a≠0）有两个实数根，且其中一个根为另一个根的2倍，那么称这样的方程为“倍根方程”．例如，一元二次方程x2﹣6x+8＝0的两个根是x1＝2和x2＝4，则方程x2﹣6x+8＝0是“倍根方程”．
（1）根据上述定义，一元二次方程x2+2x﹣8＝0 （填“是”或“不是”）“倍根方程”；
（2）若点（p，q）在双曲线y＝上，请说明关于x的方程px2+3x+q＝0是“倍根方程”；
19．【综合实践】
如图所示，是《天工开物》中记载的三千多年前中国古人利用桔槔在井上汲水的情境（杠杆原理：阻力×阻力臂＝动力×动力臂，如图，即FA×L1＝FB×L2），受桔槔的启发，小杰组装了如图所示的装置．其中，杠杆可绕支点O在竖直平面内转动，支点O距左端L1＝1m，距右端L2＝0.4m，在杠杆左端悬挂重力为80N的物体A．
（1）若在杠杆右端挂重物B，杠杆在水平位置平衡时，重物B所受拉力为 N．
（2）为了让装置有更多的使用空间，小杰准备调整装置，当重物B的质量变化时，L2的长度随之变化．设重物B的质量为xN，L2的长度为y cm．则：
①y关于x的函数解析式是 ．
②完成下表：
a＝ ，b＝ ．
③在直角坐标系中画出该函数的图象．
（3）在（2）的条件下，若点A的坐标为（20，0），B的坐标为（0，2）,在（2）所求得到函数图像中存在点C，使得S△ABC＝46．请直接写出所有满足条件的点C的坐标．
20．【问题背景】已知D、E分别是△ABC的AB边和AC边上的点，且DE∥BC，则△ABC∽△ADE，把△ADE绕着A逆时针方向旋转，连接BD和CE．
如图2，找出图中的另外一组相似三角形 ；
②若AB＝8，AC＝6，BD＝4，则CE＝ ；
【迁移应用】在Rt△ACB和Rt△ADE中，∠BAC＝∠DAE=90°，∠ABC=∠ADE＝60°，AB＝6，AC＝8,点D为线段BC上的一个动点，连接EC
如图3，写出CE比BD的的值及∠DCE的度数，并说明理由。
如图4，点P为DE中点，在点D 从B点运动到C点的过程中，请直接写出点P经过的路径长
【创新应用】如图5：，BC＝4，△ADE是直角三角形，∠DAE＝90°，tan∠ADE＝2，将△ADE绕着点A旋转，连接BE，F是BE上一点，，连接CF，请直接写出CF的取值范围．
红岭教育集团2024-2025学年度第一学期九年级期中考试数学试卷
参考答案与试题解析（请注意：部分答案对不上）
一．选择题（共9小题）
1．斗拱是中国古典建筑上的重要部件．如图是一种斗形构件“三才升”的示意图及其主视图，则它的左视图为（ ）
A．B．C．D．
【分析】左视图是从物体左面看所得到的图形．
【解答】解：从左面看，上面部分是矩形，下面部分是梯形，矩形部分有一条看不见的线，应该画虚线，
故选：C．
【点评】本题考查了三视图的概念，要注意看不见的线应当画虚线．
2．若关于x的一元二次方程x2﹣4x+c＝0有两个相等的实数根，则实数c的值为（ ）
A．﹣16B．﹣4C．4D．16
【分析】根据一元二次方程根的判别式即可解决问题．
【解答】解：因为关于x的一元二次方程x2﹣4x+c＝0有两个相等的实数根，
所以Δ＝（﹣4）2﹣4c＝0，
解得c＝4．
故选：C．
【点评】本题主要考查了根的判别式，熟知一元二次方程根的判别式是解题的关键．
3．某区为了解初中生近视情况，在全区进行初中生视力的随机抽查，结果如下表．根据抽测结果，下列对该区初中生近视的概率的估计，最合理的是（ ）
A．0.423B．0.400C．0.413D．0.410
【分析】利用大量重复实验时的频率课估计概率求解即可．
【解答】解：随着累计抽测学生数的增大，近视的学生数与n的比值逐渐稳定于0.410，
所以对该区初中生近视的概率的估计，最合理的是0.410，
故选：D．
【点评】本题主要考查利用频率估计概率，大量重复实验时，事件发生的频率在某个固定位置左右摆动，并且摆动的幅度越来越小，根据这个频率稳定性定理，可以用频率的集中趋势来估计概率，这个固定的近似值就是这个事件的概率．
4．如图，在平面直角坐标系中，已知点A（﹣1，2）、B（﹣3，﹣1），以原点O为位似中心，相似比为2，把△ABO放大，则点A的对应点A′的坐标是（ ）
A．（﹣6，﹣2）B．（﹣2，4）
C．（﹣6，﹣2）或（6，2）D．（﹣2，4）或（2，﹣4）
【分析】根据在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k，那么位似图形对应点的坐标的比等于k或﹣k计算．
【解答】解：在y轴同侧时，
∵A（﹣1，2），相似比为2，
∴A′（﹣2，4）；
在y轴两侧时，
∵A（﹣1，2），相似比为2，
∴A′（2，﹣4）；
故选：D．
【点评】本题考查的是位似变换，正确记忆相关知识点是解题关键．
5．在同一平面直角坐标系中，函数y＝﹣kx+k与的大致图象可能为（ ）
A．B．
C．D．
【分析】根据一次函数及反比例函数的图象与系数的关系作答．
【解答】解：∵一次函数y＝﹣kx+k＝﹣k（x﹣1），
∴直线经过点（1，0），A、C不合题意；
B、由一次函数的图象经过第一、三、四象限可知k＜0，反比例函数的图象在一、三象限可知k＞0，矛盾，不合题意；
D、由一次函数的图象经过第一、三、四象限可知k＜0，反比例函数的图象在二、四象限可知k＜0，一致，符合题意；
故选：D．
【点评】本题主要考查了反比例函数的图象性质和一次函数的性质，一次函数的图象上点的坐标特征，重点是注意系数k的取值．
6．如图，在平行四边形ABCD中，点E是边BA延长线一点，CE交AD于点F，下列各式中可能错误的是（ ）
A．B．C．D．
【分析】根据平行四边形的性质和相似三角形的性质求解．
【解答】解：∵AD∥BC，
∴＝，所以选项A不符合题意；
∵CD∥BE，
∴＝，
∵AB＝CD，
∴＝，所以选项B不符合题意；
∵AD∥BC，
∴△AEF∽△EBC，
∴＝，
∵AD＝BC，
∴＝，所以选项C不符合题意；
∵CD∥BE，
∴△CDF∽△EBC，
∴＝，所以选项D符合题意．
故选：D．
【点评】此题主要考查了平行线分线段成比例，相似三角形的判定与性质与平行四边形的性质，熟练利用相似三角形的性质是解答本题的关键．
7．每年春秋季节，流感盛行，极具传染性．如果一人得流感，不加干预，经过两轮后共有81人得流感，则每人每轮平均会感染几人？设每人每轮平均感染x人，则下列方程正确的是（ ）
A．（x+1）2＝81B．1+x+x2＝81
C．1+x+（x+1）2＝81D．1+（x+1）+（1+x）2＝81
【分析】设每人每轮平均感染x人，根据经过两轮后共有81人得流感，即可得出关于x的一元二次方程，此题得解．
【解答】解：设每人每轮平均感染x人，
∵1人患流感，一个人传染x人，
∴第一轮传染x人，此时患病总人数为1+x；
∴第二轮传染的人数为（1+x）x，此时患病总人数为1+x+（1+x）x＝（1+x）2，
∵经过两轮后共有81人得流感，
∴可列方程为：（1+x）2＝81．
故选：A．
【点评】本题考查了由实际问题抽象出一元二次方程，找准等量关系，正确列出一元二次方程是解题的关键．
8．如图，在正方形ABCD中，E是对角线AC上的动点，以DE为边作正方形DEFG，M是CD的中点，连接GM，若正方形ABCD的边长为8，则GM的最小值为（ ）
A．4B．C．D．2
【分析】由SAS可证△ADE和△CDG全等得AE＝CG，∠DAC＝∠DCG＝45°，由此得当点E与点A重合时，点G与点C重合，当点E与点C重合时，点G与点K重合，即当点E在线段AC上运动时，点G在线段CK上运动，根据“垂线段最短”可知：当MG⊥CK时，MG为最短，即当点G与点T重合时，MG为最小，最小值为线段MT的长，由∠DAC＝45°，MT⊥CK得△CMT为等腰直角三角形，由等腰直角三角形的性质可得GH的最小值．
【解答】解：连接CG并延长与AD的延长线交于点K，过点M作MT⊥CK于T，如图所示：
∵四边形ABCD和四边形DEFG均为正方形，
∴AD＝CD，DE＝DG，∠ADC＝60°，∠EDG＝90°，∠DAC＝45°，
∴∠ADE+∠EDC＝90°，∠CDG+∠EDC＝90°，
∴∠ADE＝∠CDG，
在△ADE和△CDG中，
，
∴△ADE≌△CDG（SAS），
∴AE＝CG，∠DAC＝∠DCG＝45°，
∴当点E与点A重合时，点G与点C重合，当点E与点C重合时，点G与点K重合，
即当点E在线段AC上运动时，点G在线段CK上运动，
根据“垂线段最短”可知：当MG⊥CK时，MG为最短，
即当点G与点T重合时，MG为最小，最小值为线段MT的长．
∵∠DAC＝45°，MT⊥CK，
∴△CMT为等腰直角三角形，即MT＝CT，
∵AB＝8，点M为CD的中点，
∴MC＝4，
由勾股定理得：MT2+CT2＝MC2，
∴2MT2＝16，
∴MT＝2．
∴GM的最小值为2，
故选：C．
【点评】本题考查了正方形的性质，全等三角形三角形的判定和性质，勾股定理等，理解正方形的性质，熟练掌握全等三角形三角形的判定和性质是解决问题的关键．
9．如图，将矩形ABCD对折，使AB与CD边重合，得到折痕MN，再将点A沿过点D的直线折叠到MN上，对应点为A′，折痕为DE，AB＝10，BC＝6，则A′N的长度为（ ）
A．B．4C．D．3
【分析】由折叠的性质得，AM＝DM＝，∠DMA'＝∠AMA'＝90°，AD＝A'D，由勾股定理求出A'M的长，再证四边形ABNM是矩形，即可求出A′N的长．
【解答】解：由折叠的性质得，AM＝DM＝，∠DMA'＝∠AMA'＝90°，AD＝A'D，
∵四边形ABCD是矩形，
∴AD＝BC，∠A＝∠B＝90°，
∵BC＝6，
∴AD＝6，
∴DM＝3，
在Rt△DMA'中，由勾股定理得A'M＝，
∵∠A＝∠B＝∠AMA'＝90°，
∴四边形ABNM是矩形，
∴MN＝AB＝10，
∴A′N＝MN﹣A'M＝10﹣，
故选：A．
【点评】本题考查了矩形的判定与性质，折叠问题，勾股定理，熟练掌握这些知识点是解题的关键．
二．填空题（共3小题）
10．已知，则＝ ．
【分析】由a、b的关系变形，用一个字母表示另一个，代入即可得解．
【解答】解：∵，
∴b＝2a，
∴＝，
故答案为：．
【点评】本题考查了比例的基本性质，变形求解是解题的关键．
11．《周髀算经》中记载了“偃矩以望高”的方法．“矩”在古代指两条边呈直角的曲尺（即图中的ABC）．“偃矩以望高”的意思是把“矩”仰立放，可测量物体的高度．如图，是用“矩”测量一个5G信号塔高度的示意图，点A，B，N在同一水平线上，∠ABC和∠ANM均为直角，AM与BC交于点D，测得AB＝40cm，BD＝30cm，BN＝22m，则信号塔MN的高度为 16.8 m．
【分析】由题意可知，AN＝22.4m，BD＝0.3m，证明△ABD∽△ANM，得到，即可求出信号塔MN的高度．
【解答】解：∵AB＝40cm＝0.4m，BN＝22m，
∴AN＝AB+BN＝22.4m，
∵∠ABC＝∠ANM＝90°，
∴BC∥MN，
∴△ABD∽△ANM，
∴，
∴，
∴MN＝16.8m，
故答案为：16.8．
【点评】本题考查相似三角形的判定与性质，解答本题的关键是明确题意，利用数形结合的思想解答．
12．如图，点A在反比例函数y＝（k≠0）的图象上，且点A是线段OB的中点，点D为x轴上一点，连接BD交反比例函数图象于点C，连接AC，若BC：CD＝2：1，S△ADC＝，则k的值为 16 ．
【分析】作AE⊥OD于E，CF⊥OD于F．首先证明S△AOC＝S△AOE+S梯形AEFC﹣S△OCF＝S梯形AEFC，由此构建方程即可解决问题；
【解答】解：作AE⊥OD于E，CF⊥OD于F．
∵BC：CD＝2：1，S△ADC＝，
∴S△ACB＝，
∵OA＝AB，
∴B（2m，2n），S△AOC＝S△ACB＝，
∵A、C在y＝上，BC＝2CD，
∴C（m，n），
∵S△AOC＝S△AOE+S梯形AEFC﹣S△OCF＝S梯形AEFC，
∴•（n+n）×m＝，
∴mn＝16，
∵A（m，n），
∴k＝16．
故答案为16
【点评】本题考查反比例函数系数k的几何意义，解题的关键是学会利用参数，构建方程解决问题，本题的突破点是证明S△AOC＝S△AOE+S梯形AEFC﹣S△OCF＝S梯形AEFC．
三．解答题（共8小题）
13．数学实验，能增加学习数学的乐趣，还能经历知识“再创造”的过程，更是培养动手能力，创新能力的一种手段．小强在学习《相似》一章中对“直角三角形斜边上作高”这一基本图形（如图1）产生了如下问题，请同学们帮他解决．
在△ABC中，点D为边AB上一点，连接CD．
（1）初步探究
如图2，若∠ACD＝∠B，求证：AC2＝AD•AB；
（2）尝试应用
如图3，在（1）的条件下，若点D为AB中点，BC＝4，求CD的长；
（3）创新提升
如图4，点E为CD中点，连接BE，若∠CDB＝∠CBD＝30°，∠ACD＝∠EBD，AC＝2，求BE的长．
【分析】（1）由∠A＝∠A，∠ACD＝∠B，证明△ACD∽△ABC，得＝，则AC2＝AD•AB；
（2）设AD＝m，则AD＝BD＝m，AB＝2m，根据相似三角形的性质得＝＝，则AC2＝2m2，求得AC＝m，所以＝＝，而BC＝4，则CD＝BC＝2；
（3）解法一，作BF⊥DC交DC的延长线于点F，设CE＝DE＝n，则CB＝CD＝2n，再证明∠FBC＝30°，所以CF＝CB＝n，求得EF＝2n，BF＝n，则BD＝2n，BE＝n，作CH∥EB交AB的延长线于点H，则△HDC∽△BDE，所以＝＝＝2，则HC＝2n，HD＝4n，再证明△ACD∽△AHC，得＝＝＝，则AD＝AC＝2，AH＝AC＝14，所以HD＝4n＝12，则n＝，求得BE＝．
解法二，取BD中点M，连接CM、EM，则EM∥CB，由∠CDB＝∠CBD＝30°，得CD＝CB，∠EMD＝∠CBD＝30°，则CM⊥BD，∠ADC＝∠BME，可证明△ACD∽△EBM，设CM＝x，则CD＝CB＝2x，BM＝x，所以＝＝，则BE＝AC＝．
【解答】（1）证明：如图2，∵∠A＝∠A，∠ACD＝∠B，
∴△ACD∽△ABC，
∴＝，
∴AC2＝AD•AB．
（2）解：如图3，设AD＝m，
∵点D为AB中点，
∴AD＝BD＝m，AB＝2m，
由（1）得△ACD∽△ABC，
∴＝＝，
∴AC2＝AD•AB＝m×2m＝2m2，
∴AC＝m或AC＝m（不符合题意，舍去），
∴＝＝＝，
∵BC＝4，
∴CD＝BC＝×4＝2，
∴CD的长是2．
（3）解法一：如图4，作BF⊥DC交DC的延长线于点F，则∠F＝90°，
∵点E为CD中点，
∴CE＝DE，
设CE＝DE＝n，
∵∠CDB＝∠CBD＝30°，
∴CB＝CD＝2n，∠BCF＝∠CDB+∠CBD＝60°，
∴∠FBC＝90°﹣∠BCF＝30°，
∴CF＝CB＝n，
∴EF＝CE+CF＝2n，BF＝＝＝n，
∴BD＝2BF＝2n，BE＝＝＝n，
作CH∥EB交AB的延长线于点H，则△HDC∽△BDE，
∴＝＝＝＝2，
∴HC＝2BE＝2n，HD＝2BD＝4n，
∵∠ACD＝∠EBD，∠H＝∠EBD，
∴∠ACD＝∠H，
∵∠A＝∠A，
∴△ACD∽△AHC，
∴＝＝＝＝＝，
∵AC＝2，
∴AD＝AC＝×2＝2，AH＝AC＝×2＝14，
∴HD＝AH﹣AD＝14﹣2＝12，
∴4n＝12，
解得n＝，
∴BE＝×＝，
∴BE的长是．
解法二：如图5，取BD中点M，连接CM、EM，
∵点E为CD中点，
∴DM是△BCD的中位线，
∴EM∥CB，
∵∠CDB＝∠CBD＝30°，
∴CD＝CB，∠EMD＝∠CBD＝30°，
∴CM⊥BD，∠ADC＝∠BME＝180°﹣30°＝150°，
∵∠ACD＝∠EBD，即∠ACD＝∠EBM，
∴△ACD∽△EBM，
∵∠CMB＝90°，∠CBM＝30°，AC＝2，
∴CD＝CB＝2CM，
设CM＝x，则CD＝CB＝2x，
∴BM＝＝＝x，
∴＝＝＝，
∴BE＝AC＝×2＝，
∴BE的长是．
【点评】此题重点考查相似三角形的判定与性质、直角三角形中30°角所对的直角边等于斜边的一半、勾股定理等知识，此题综合性强，难度较大，正确地作出辅助线是解题的关键．
14．（1）计算：；
（2）解方程：x2﹣4x﹣5＝0．
【分析】（1）先计算绝对值、负整数指数幂、零指数幂，再计算加减即可得解；
（2）利用因式分解法解一元二次方程即可．
【解答】解：（1）原式＝
＝；
（2）x2﹣4x﹣5＝0，
因式分解得：（x﹣5）（x+1）＝0，
则x﹣5＝0或x+1＝0，
解得：x1＝5，x2＝﹣1．
【点评】本题考查了实数的混合运算、解一元二次方程，熟练掌握运算方法是解此题的关键．
15．2024年4月21日，达州马拉松暨“跑遍四川”达州站马拉松赛鸣枪开跑，本次赛事以“相约巴人故里，乐跑红色达州”为主题，旨在增强全市民众科学健身意识，推动全民健身活动．本届赛事共设置马拉松，半程马拉松和欢乐跑三个项目．赛后随机抽取了部分参赛选手对本次赛事组织进行满意度评分调查，整理后得到下列不完整的图表：
请根据表中提供的信息，解答下列问题：
（1）此次调查共抽取了 800 名选手，m＝ 40 ，n＝ 5 ；
（2）扇形统计图中，B等级所对应的扇形圆心角度数是 126 度；
（3）赛后若在三个项目的冠军中随机抽取两人访谈，请用列表或画树状图的方法，求出恰好抽到马拉松和欢乐跑冠军的概率．
【分析】（1）先用A等级人数除以它所占的百分比得到调查的总人数，再用总人数乘以C等级所占的百分比得到m的值，然后D等级人数乘以调查的总人数得到n的值；
（2）用360°乘以B等级所占的百分比即可；
（3）用A、B、C分别表示马拉松，半程马拉松和欢乐跑三个项目．则通过画树状图展示所有6种等可能的结果，再找出马拉松和欢乐跑冠军的结果数，然后根据概率公式求解．
【解答】解：（1）此次调查共抽取的选手总人数为440÷55%＝800（名）；
所以m＝800×5%＝40，
所以n%＝＝5%，
即n＝5；
故答案为：800，40，5；
（2）扇形统计图中，B等级所对应的扇形圆心角度数＝360°×＝126°；
故答案为：126；
（3）用A、B、C分别表示马拉松，半程马拉松和欢乐跑三个项目．
画树状图为：
共有6种等可能的结果，其中马拉松和欢乐跑冠军的结果数为2种，
所以恰好抽到马拉松和欢乐跑冠军的概率＝＝．
【点评】本题考查了列表法与树状图法：利用列表法或树状图展示所有可能的结果求出n，再从中选出符合事件A或B的结果数目m，然后利用概率公式求出事件A或B的概率．也考查了统计图．
16．2024年巴黎奥运会顺利闭幕，吉祥物“弗里热”深受奥运迷的喜爱，一商场以20元的进价进一批“弗里热”纪念品，以30元每个的价格售出，每周可以卖出500个，经过市场调查发现，价格每涨5元，就少卖50个．
（1）若商场计划一周的利润达到8000元，并且更大优惠让利消费者，售价应定为多少钱？
（2）因商场改变销售策略，在不改变（1）的销售价格基础上，销售量稳步提升，两周后销售量达到了484个，求这两周的平均增长率．
【分析】（1）设售价应定为x元，则每个利润为（x﹣20）元，销量为个，利用总利润为8000元，列出一元二次方程，解之取符合题意的值即可；
（2）由（1）得：当售价为每个40元时，销量为400个，设这两周的平均增长率为y，根据两周后销售量达到了484个，列出一元二次方程，解之取符合题意的值即可．
【解答】解：（1）设售价应定为x元，则每个利润为（x﹣20）元，销量为个，
由题意得：，
整理得：x2﹣100x+2400＝0，
解得：x1＝40，x2＝60（不符合题意，舍去），
答：商场计划一周的利润达到8000元，并且更大优惠让利消费者，售价应定为40元；
（2）由（1）得：当售价为40元时，销量为400个，
设这两周的平均增长率为y，
由题意得：400（1+y）2＝484，
解得：y1＝0.1＝10%，y2＝﹣2.1（不符合题意，舍去），
答：这两周的平均增长率为10%．
【点评】本题考查了一元二次方程的应用，找准等量关系，正确列出一元二次方程是解题的关键．
17．如图，在菱形ABCD中，对角线AC，BD相交于点O，延长CB到点E，使得BE＝BC．连接AE．过点B作BF∥AC，交AE于点F，连接OF．
（1）求证：四边形AFBO是矩形；
（2）若∠E＝30°，BF＝1，求OF的长．
【分析】（1）证四边形ADBE是平行四边形，再证AE⊥AC，则∠OAF＝90°，然后由矩形的判定即可得出结论；
（2）由矩形的性质得∠AFB＝90°，OF＝AB，所以∠BFE＝90°．又由∠E＝30°，BF＝1，由直角三角形性质得BE＝2BF＝2．在Rt△AEC中，BE＝BC，由直角三角形性质得AB＝BE＝2，即可得出结论．
【解答】（1）证明：∵四边形ABCD是菱形，
∴AD∥BC，AC⊥BD，AD＝BC，
∵BE＝BC，
∴AD＝BE，
∴四边形AEBD是平行四边形，
∴AE∥BD．
∵BF∥AC，
∴四边形AFBO是平行四边形．
∵AC⊥BD，AE∥BD
∴AE⊥AC，
∴∠OAF＝90°，
∴平行四边形AFBO是矩形．
（2）解：由（1）知四边形AFBO是矩形，
∴∠AFB＝90°，OF＝AB，
∴∠BFE＝90°．
又∵∠E＝30°，BF＝1，
∴BE＝2BF＝2．
在Rt△AEC中，BE＝BC，
∴AB＝BE＝2，
∴OF＝2．
【点评】本题考查了矩形的判定与性质、菱形的性质、平行四边形的判定与性质、直角三角形的性质，熟练掌握矩形的判定与性质，菱形的性质、直角三角形的性质是解题的关键．
18．如果关于x的一元二次方程ax2+bx+c＝0（a≠0）有两个实数根，且其中一个根为另一个根的2倍，那么称这样的方程为“倍根方程”．例如，一元二次方程x2﹣6x+8＝0的两个根是x1＝2和x2＝4，则方程x2﹣6x+8＝0是“倍根方程”．
（1）根据上述定义，一元二次方程x2+2x﹣8＝0 不是 （填“是”或“不是”）“倍根方程”；
（2）若点（p，q）在双曲线y＝上，请说明关于x的方程px2+3x+q＝0是“倍根方程”；
（3）若（x﹣2）（mx﹣n）＝0（m≠0）是“倍根方程”，求代数式的值．
【分析】（1）根据“倍根方程”的定义即可得出结论；
（2）方程px2+3x+q＝0化为方程px2+3x+＝0，解方程求得方程的根，根据倍根方程的定义即可求出答案．
（3）根据定义可求出n＝4m或n＝m，代入原式后即可求出答案；
【解答】解：（1）x2+2x﹣8＝0，
（x﹣2）（x+4）＝0，
解得x1＝2，x2＝﹣4，
故一元二次方程x2+2x﹣8＝0 不是“倍根方程”．
（2）∵点（p，q）在双曲线y＝上，
∴q＝，
∴方程px2+3x+q＝0化为方程px2+3x+＝0，
（px+1）（px+2）＝0，
解得x1＝﹣，x2＝﹣，
∴方程px2+3x+q＝0是“倍根方程”．
（3）由（x﹣2）（mx﹣n）＝0（m≠0）是“倍根方程”，
且该方程的两根分别为x＝2和x＝，
∴＝4或＝1，
当n＝4m时，
原式＝＝，
当n＝m时，
原式＝＝1．
故代数式的值为或1．
【点评】本题考查一元二次方程，解题的关键是熟练运用一元二次方程的解法以及正确理解“倍根方程”的定义，本题属于中等题型．
19．【综合实践】
如图所示，是《天工开物》中记载的三千多年前中国古人利用桔槔在井上汲水的情境（杠杆原理：阻力×阻力臂＝动力×动力臂，如图，即FA×L1＝FB×L2），受桔槔的启发，小杰组装了如图所示的装置．其中，杠杆可绕支点O在竖直平面内转动，支点O距左端L1＝1m，距右端L2＝0.4m，在杠杆左端悬挂重力为80N的物体A．
（1）若在杠杆右端挂重物B，杠杆在水平位置平衡时，重物B所受拉力为 200 N．
（2）为了让装置有更多的使用空间，小杰准备调整装置，当重物B的质量变化时，L2的长度随之变化．设重物B的质量为xN，L2的长度为y cm．则：
①y关于x的函数解析式是 ．
②完成下表：
a＝ 4 ，b＝ ．
③在直角坐标系中画出该函数的图象．
（3）在（2）的条件下，将函数图象向右平移4个单位长度，与原来的图象组成一个新的函数图象，记为L．若点A的坐标为（2，0），在L上存在点Q，使得S△OAQ＝9．请直接写出所有满足条件的点Q的坐标．
【分析】（1）根据公式FA×L1＝FB×L2进行计算即可；
（2）①根据公式FA×L1＝FB×L2即可得到；②根据（2）①所求求出a、b的值即可；③先描点，再连线，画出函数图象即可；
（3）先根据面积求出点Q的纵坐标，再根据反比例函数性质和平移的性质求出点Q的坐标即可．
【解答】解：（1）∵FA×L1＝FB×L2，
∴，
∴重物B所受拉力为200N，
故答案为：200；
（2）①∵FA×L1＝FB×L2，
∴，即，
故答案为：；
②由（2）①得，
填表如下：
③函数图象如下所示：
故答案为：4，；
（3）∵点A的坐标为（2，0），
∴OA＝2，
∵S△OAQ＝9，
∴，
∴yQ＝9，
在中，当y＝9时，
∴在函数上满足题意的Q的坐标为，
∵将函数图象向右平移4个单位长度，与原来的图象组成一个新的函数图象，记为L，
∴点，即也在L上，即满足题意的Q的坐标为；
综上所述，点Q的坐标为或．
【点评】本题属于三角形综合题，主要考查了反比例函数的实际运用，正确理解题意是解题的关键．
20．【问题背景】已知D、E分别是△ABC的AB边和AC边上的点，且DE∥BC，则△ABC∽△ADE，把△ADE绕着A逆时针方向旋转，连接BD和CE．
①如图2，找出图中的另外一组相似三角形 △BAD∽△CAE ；
②若AB＝4，AC＝3，BD＝2，则CE＝ ；
【迁移应用】在Rt△ACB中，∠BAC＝90°，∠C＝60°，D、E，M分别是AB、AC、BC中点，连接DE和CM．
①如图3，写出CE和BD的数量关系 BD＝EC ；
②如图4，把Rt△ADE绕着点A逆时针方向旋转，当D落在AM上时，连接CD和CE，取CD中点N，连接MN，若，求MN的长．
【创新应用】如图5：，BC＝4，△ADE是直角三角形，∠DAE＝90°，tan∠ADE＝2，将△ADE绕着点A旋转，连接BE，F是BE上一点，，连接CF，请直接写出CF的取值范围．
【分析】【问题背景】①结论：△BAD∽△CAE．利用两边成比例夹角相等两三角形相似证明；
②利用相似三角形的性质求解；
【迁移应用】①结论：BD＝CE，证明AB＝AC，可得结论；
②连接BD，利用相似三角形的性质，求出BD，再利用三角形的中位线定理求解即可；
【创新应用】如图5中，过点A作AK⊥BC于点K，过点C作CJ⊥AB于点J，连接FJ．通过计算证明FJ∥AE，求出JF，JC，可得结论．
【解答】解：【问题背景】①如图2中，∵△ABC∽△ADE，
∴＝，
∴＝，
∵∠BAC＝∠DAE，
∴∠BAD＝∠CAE，
∴△BAD∽△CAE．
故答案为：△BAD∽△CAE；
②∵△BAD∽△CAE，
∴＝，
∴＝，
∴CE＝．
故答案为：；
【迁移应用】①如图3中，在Rt△ABC中，∠BAC＝90°，∠C＝60°，
∴tan60°＝，
∴AB＝AC，
∵BD＝AB，EC＝AC，
∴BD＝EC．
故答案为：BD＝EC；
②如图4中，连接BD，MN．
∵∠BAC＝∠DAE＝90°，
∴∠BAD＝∠CAE，
∵＝＝，
∴△BAD∽△CAE，
∴＝＝，
∵EC＝2，
∴BD＝6，
∵BM＝CM，DN＝CN，
∴MN＝BD＝3；
【创新应用】如图5中，过点A作AK⊥BC于点K，过点C作CJ⊥AB于点J，连接FJ．
∵AB＝AC＝2，AK⊥BC，
∴BK＝CK＝2，
∴AK＝＝＝4，
∵•BC•AK＝•AB•CJ，
∴CJ＝，
∴AJ＝＝＝，
∴BJ＝AJ＝2﹣＝，
∴BJ：AB＝2：5，
∵BF：BE＝2：5，
∴＝＝，
∴FJ∥AE，
∴△BJF∽△BAE，
∴＝＝，
∴JF＝AE＝，
∴CJ﹣JF≤CF≤FJ+CJ，
∴≤CF≤．
【点评】本题属于相似形综合题，考查了相似三角形的判定和性质，解直角三角形，三角形中位线定理，平行线的判定和性质等知识，解题的关键是学会添加常用辅助线，构造平行线解决问题，属于中考压轴题．
累计抽测的学生数n
100
200
300
400
500
600
800
近视学生数与n的比值
0.423
0.410
0.400
0.401
0.413
0.409
0.410
等级
A
B
C
D
分数段
90﹣100
80﹣89
70﹣79
60﹣69
频数
440
280
m
40
x/N
…
10
20
30
40
50
…
y/cm
…
8
a
2
b
…
累计抽测的学生数n
100
200
300
400
500
600
800
近视学生数与n的比值
0.423
0.410
0.400
0.401
0.413
0.409
0.410
等级
A
B
C
D
分数段
90﹣100
80﹣89
70﹣79
60﹣69
频数
440
280
m
40
x/N
…
10
20
30
40
50
…
y/cm
…
8
a
2
b
…
x/N
…
10
20
30
40
50
…
y/cm
…
8
4
2
…