


福建省莆田第八中学2024-2025学年八年级上学期期中考数学试题
展开
这是一份福建省莆田第八中学2024-2025学年八年级上学期期中考数学试题,文件包含福建省莆田市荔城区莆田第八中学2024-2025学年八年级上学期期中考数学试卷docx、福建省莆田市荔城区莆田第八中学2024-2025学年八年级上学期期中考数学答案docx等2份试卷配套教学资源,其中试卷共9页, 欢迎下载使用。
1—5: BDDCD 6—10: ABBAB
二、填空题(共24分)
11. 稳定 12. 7 13. 14
14. 16 15. 3:4 16. ①②③
三、解答题(共86分).
17.(8分) 解:设此多边形的边数为n,则:
(n﹣2)•180=1440+360,
解得:n=12.
答:这个多边形的边数为12.
18.(8分)证明:过点A作AF⊥BC于点F.
∵AD=AE,AF⊥BC,
∴DF=EF,
∵BD=CE,
∴BF=FC,
∵AF⊥BC,
∴AB=AC.
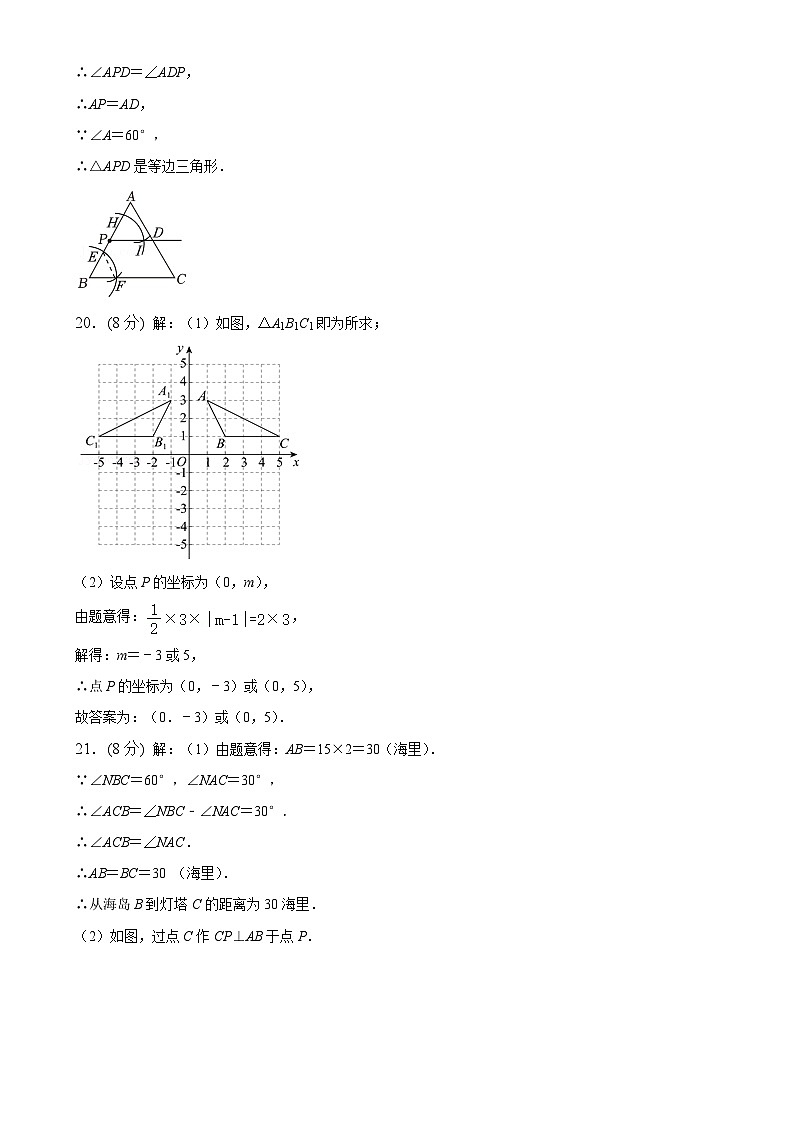
19.(8分) (1)解:作法:1.以点B为圆心,适当长度为半径作弧,分别交AB、BC于点E、F;
2.以点P为圆心,以BE的长为半径作弧,交PA于点H;
3.连接EF,以点H为圆心,以EF长为半径作弧,交前弧于点I;
4.作射线PI交AC于点I,交AC于点D,
则点D就是所求的图形.
证明:由作图得∠APD=∠B,
∴PD∥BC,
∴点D就是所求的图形.
(2)证明:∵PD∥BC,
∴∠APD=∠B,∠ADP=∠C,
∵AB=AC,
∴∠B=∠C,
∴∠APD=∠ADP,
∴AP=AD,
∵∠A=60°,
∴△APD是等边三角形.
20.(8分) 解:(1)如图,△A1B1C1即为所求;
(2)设点P的坐标为(0,m),
由题意得:,
解得:m=﹣3或5,
∴点P的坐标为(0,﹣3)或(0,5),
故答案为:(0.﹣3)或(0,5).
21.(8分) 解:(1)由题意得:AB=15×2=30(海里).
∵∠NBC=60°,∠NAC=30°,
∴∠ACB=∠NBC﹣∠NAC=30°.
∴∠ACB=∠NAC.
∴AB=BC=30 (海里).
∴从海岛B到灯塔C的距离为30海里.
(2)如图,过点C作CP⊥AB于点P.
∴根据垂线段最短,线段CP的长为小船与灯塔C的最短距离,∠BPC=90°.
又∵∠NBC=60°,
∴∠PCB=180°﹣∠BPC﹣∠CBP=30°.
在Rt△CBP中,∠BCP=30°,
∴(海里),
∴AP=AB+BP=30+15=45(海里).
∴航行的时间为45÷15=3(时).
∴若这条船继续向正北航行,上午11时小船与灯塔C的距离最短.
22.(10分) (1)证明:连接BP、CP,
∵点P在BC的垂直平分线上,
∴BP=CP,
∵AP是∠DAC的平分线,
∴DP=EP,
在Rt△BDP和Rt△CEP中,,
∴Rt△BDP≌Rt△CEP(HL),
∴BD=CE;
(2)解:在Rt△ADP和Rt△AEP中,,
∴Rt△ADP≌Rt△AEP(HL),
∴AD=AE,
∵AB=6cm,AC=10cm,
∴6+AD=10﹣AE,
即6+AD=10﹣AD,
解得AD=2cm.
23.(10分) 解:(1)①∵△ABC是“奇妙互余三角形”,∠C>90°,
∴α,β只能是∠A和∠B,
∵2α+β=90°,∠A=60°,
∴2α+60°=90°或2×60°+β=90°,
解得:α=15°,β=﹣30(不合题意舍去),
∴∠B=15°,
故答案为:15°;
②∵△ABC是“奇妙互余三角形”,∠C>90°,
∴α,β只能是∠A和∠B,
∵2α+β=90°,∠A=40°,
∴2α+40°=90°或2×40°+β=90°,
解得:α=25°,β=10°(不合题意舍去),
∴∠B=25°或10°,
∴∠C=180°﹣∠A﹣∠B=115°或130°,
故答案为:115°或130°;
(2)如图,当点P在线段BC上时,此时∠APB>90°,
∵△ABP是“奇妙互余三角形”,
∴2∠BAP+∠ABP=90°或∠BAP+2∠ABP=90°,
即2∠BAP+52°=90°或∠BAP+2×52°=90°,
解得:∠BAP=19°或-14°(不符合题意,舍去),
∴∠APC=∠BAP+∠ABP=71°;
当点P在线段CB的延长线上时,∠APB<90°,如图所示:
此时∠ABC=∠BAP+∠APC=52°,
∵△ABP是“奇妙互余三角形”,
∴2∠BAP+∠APB=90°或∠BAP+2∠APB=90°,
解得:∠BAP=38°或14°,
∴∠APC=∠ABC﹣∠BAP=14°或38°;
综上可知:∠APC的度数为71°或14°或38°.
24.(12分)
解:(1)延长AD到Q,使得DQ=AD,再连接BQ,
∵AD是△ABC的中线,
∴BD=CD,
又∵DQ=AD,∠BDQ=∠CDA,
∴△BDQ≌△CDA(SAS),
∴BQ=CA=5,
在△ABQ中,AB﹣BQ<AQ<AB+BQ,
∴9﹣5<AQ<9+5,
即4<AQ<14,
∴2<AD<7,
故答案为:2<AD<7;
(2)①答:BE=EF+CF.
证明:如图2,延长AD至点G,使GD=ED,连接CG,
∵AD为BC边上的中线,
∴BD=CD,
在△EDB和△GDC中,
BD=CD∠EDB=∠GDCED=GD
∴△EDB≌△GDC(SAS),
∴BE=CG,∠G=∠BED,
∵AF=EF,
∴∠EAF=∠AEF,
∵∠BED=∠AEF
∴∠G=∠BED=∠AEF=∠EAF,
∴CG=AC, ∴BE=AC.
∴BE=AC=AF+CF=EF+CF.
②解:如图,延长AD至点M,使DM=AE,连接BM,
∵AE=DM,
∴AE+ED=DM+ED
即AD=EM,
∵AF=EF,
∴∠AEF=∠EAF,
∴∠BEM=∠AEF=∠CAD,
又由①中已证BE=AC,
∴△ACD≌△EBM(SAS),
∴CD=BM
∵BD=CD=AE=DM
∴BD=DM=BM,
∴△BDM为等边三角形.
∴∠BDM=60°,
∴∠ADC=∠BDM=60°.
则∠ADB的度数为60°.
(14分)
(1)证明:如图1中,∵△CDE为等腰直角三角形,∠DCE=90°.
∴CD=CE,∠DCB+∠ECF=90°,
∵EF⊥BC,
∴∠ECF+∠CEF=90°,
∴∠DCB=∠CEF,
在△DBC和△CEF中,
,
∴△DBC≌△CFE(AAS);
(2)解:如图2中,∵△DBC≌△CFE,
∴BD=CF,BC=EF,
∵△ABC为等腰直角三角形,
∴AB=BC,
∴AB=EF,AD=BF,
在△ABM和△EFM中,
,
∴△ABM≌△EFM(AAS),
∴BM=FM,
∴BF=2BM, ∴AD=2BM;
(3)解:结论:=1.
在EH上截取EQ=DG,连接CQ如图,
在△CDG和△CEQ中
,
∴△CDG≌△CEQ(SAS),
∴CG=CQ,∠DCG=∠ECQ,
∵∠DCG+∠DCB=45°,
∴∠ECQ+∠DCB=45°,
而∠DCE=90°,
∴∠HCQ=45°,
∴∠HCQ=∠HCG,
在△HCG和△HCQ中,
,
∴△HCG≌△HCQ(SAS),
∴HG=HQ,
∴HE=HQ+QE=HG+DG,
∴=1.
相关试卷
这是一份福建省莆田市荔城区莆田第八中学2024-2025学年八年级上学期数学期中考试试卷(无答案),共2页。试卷主要包含了选择题.,填空题.,解答题.等内容,欢迎下载使用。
这是一份福建省莆田中山中学2024-2025学年上学期期中考试九年级数学试题,共6页。
这是一份2024年福建省莆田哲理中学中考一模数学试题,共8页。试卷主要包含了-3的倒数是,如图,数轴上点P表示的数可能是,已知点M等内容,欢迎下载使用。








