




所属成套资源:【讲通练透】2025年新高考数学一轮复习(新教材,含2024高考真题)
第02讲 两条直线的位置关系(八大题型)(讲义)-2025年高考数学一轮复习讲练测(新教材新高考)
展开这是一份第02讲 两条直线的位置关系(八大题型)(讲义)-2025年高考数学一轮复习讲练测(新教材新高考),文件包含第02讲两条直线的位置关系八大题型讲义原卷版docx、第02讲两条直线的位置关系八大题型讲义解析版docx等2份试卷配套教学资源,其中试卷共55页, 欢迎下载使用。
\l "_Tc176520995" 01 考情透视·目标导航 PAGEREF _Tc176520995 \h 2
\l "_Tc176520996" 02 知识导图·思维引航 PAGEREF _Tc176520996 \h 3
\l "_Tc176520997" 03 考点突破·题型探究 PAGEREF _Tc176520997 \h 4
\l "_Tc176520998" 知识点1:直线平行与垂直的判定 PAGEREF _Tc176520998 \h 4
\l "_Tc176520999" 知识点2:三种距离 PAGEREF _Tc176520999 \h 5
\l "_Tc176521000" 解题方法总结 PAGEREF _Tc176521000 \h 5
\l "_Tc176521001" 题型一:两直线位置关系的判定 PAGEREF _Tc176521001 \h 7
\l "_Tc176521002" 题型二:两直线的交点与距离问题 PAGEREF _Tc176521002 \h 9
\l "_Tc176521003" 题型三:有关距离的最值问题 PAGEREF _Tc176521003 \h 14
\l "_Tc176521004" 题型四:点关于点对称 PAGEREF _Tc176521004 \h 23
\l "_Tc176521005" 题型五:点关于线对称 PAGEREF _Tc176521005 \h 25
\l "_Tc176521006" 题型六:线关于点对称 PAGEREF _Tc176521006 \h 27
\l "_Tc176521007" 题型七:线关于线对称 PAGEREF _Tc176521007 \h 29
\l "_Tc176521008" 题型八:直线系方程 PAGEREF _Tc176521008 \h 31
\l "_Tc176521009" 04真题练习·命题洞见 PAGEREF _Tc176521009 \h 33
\l "_Tc176521010" 05课本典例·高考素材 PAGEREF _Tc176521010 \h 34
\l "_Tc176521011" 06易错分析·答题模板 PAGEREF _Tc176521011 \h 37
\l "_Tc176521012" 易错点:两平行直线间的距离公式应用错误 PAGEREF _Tc176521012 \h 37
\l "_Tc176521013" 答题模板:已知两直线平行或垂直求参数 PAGEREF _Tc176521013 \h 37
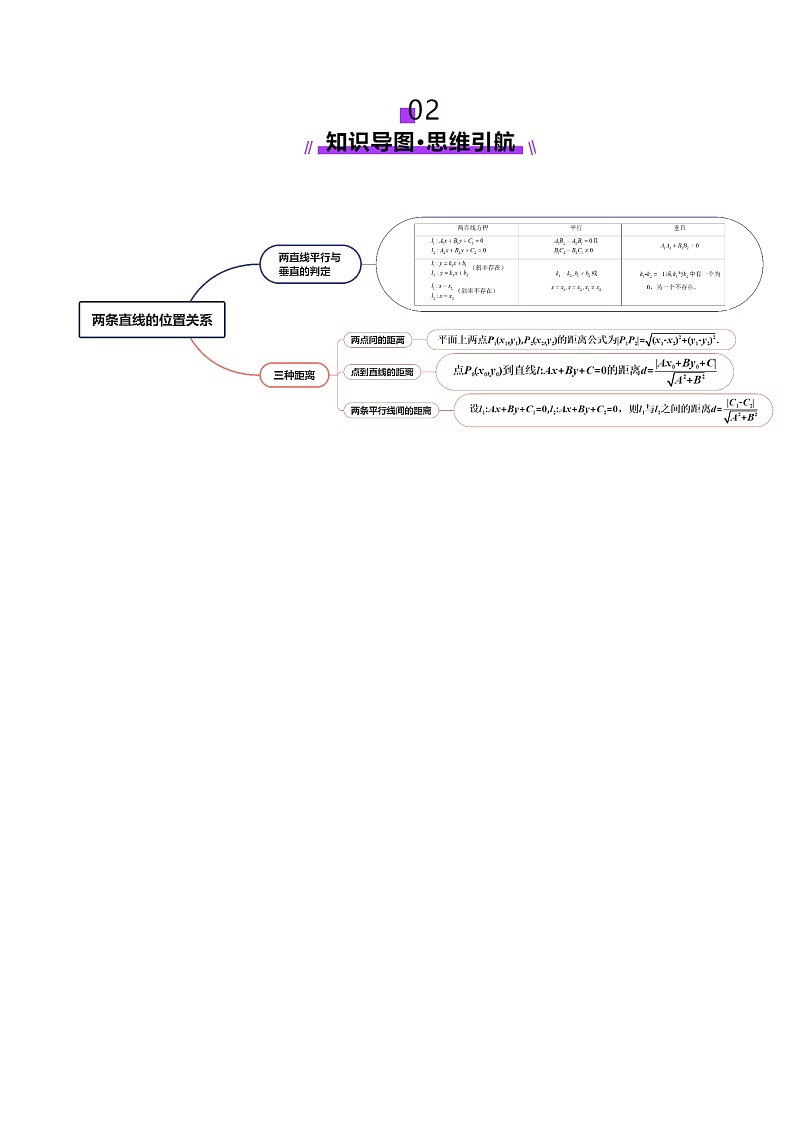
知识点1:直线平行与垂直的判定
两条直线平行与垂直的判定以表格形式出现,如表所示.
【诊断自测】(多选题)已知两条直线,的方程分别为与,下列结论正确的是( )
A.若,则B.若,则两条平行直线之间的距离为
C.若,则D.若,则直线,一定相交
【答案】AD
【解析】两条直线,的方程分别为与,它们不重合,
若,则,得,检验符合,故A选项正确;
若,由A选项可知,:,直线的方程可化为,
故两条平行直线之间的距离为,故B选项不正确;
若,则,得,故C选项不正确;
由A选项知,当时,,所以若,则直线,一定相交,故D选项正确.
故选:AD.
知识点2:三种距离
1、两点间的距离
平面上两点的距离公式为.
特别地,原点O(0,0)与任一点P(x,y)的距离
2、点到直线的距离
点到直线的距离
特别地,若直线为l:x=m,则点到l的距离;若直线为l:y=n,则点到l的距离
3、两条平行线间的距离
已知是两条平行线,求间距离的方法:
(1)转化为其中一条直线上的特殊点到另一条直线的距离.
(2)设,则与之间的距离
注:两平行直线方程中,x,y前面对应系数要相等.
4、双根式
双根式型函数求解,首先想到两点间的距离,或者利用单调性求解.
【诊断自测】(多选题)已知点到直线的距离为3,则实数等于( )
A.0B.C.3D.2
【答案】AB
【解析】依题意,即,解得或.
故选:AB.
解题方法总结
1、点关于点对称
点关于点对称的本质是中点坐标公式:设点关于点的对称点为,则根据中点坐标公式,有
可得对称点的坐标为
2、点关于直线对称
点关于直线对称的点为,连接,交于点,则垂直平分,所以,且为中点,又因为在直线上,故可得,解出即可.
3、直线关于点对称
法一:在已知直线上取两点,利用中点坐标公式求出它们关于已知点对称的两点坐标,再由两点式求出直线方程;
法二:求出一个对称点,再利用两对称直线平行,由点斜式得到所求直线方程.
4、直线关于直线对称
求直线,关于直线(两直线不平行)的对称直线
第一步:联立算出交点
第二步:在上任找一点(非交点),利用点关于直线对称的秒杀公式算出对称点
第三步:利用两点式写出方程
5、常见的一些特殊的对称
点关于轴的对称点为,关于轴的对称点为.
点关于直线的对称点为,关于直线的对称点为.
点关于直线的对称点为,关于直线的对称点为.
点关于点的对称点为.
点关于直线的对称点为,关于直线的对称点为.
6、过定点直线系
过已知点的直线系方程(为参数).
7、斜率为定值直线系
斜率为的直线系方程(是参数).
8、平行直线系
与已知直线平行的直线系方程(为参数).
9、垂直直线系
与已知直线垂直的直线系方程(为参数).
10、过两直线交点的直线系
过直线与的交点的直线系方程:(为参数).
题型一:两直线位置关系的判定
【典例1-1】(湖北省“宜荆荆恩”2024届高三9月起点考试数学试题)已知两条直线,则“”是“”的( )
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
【答案】A
【解析】当时,,则,
所以“”是“”的充分不必要条件.
故选:A
【典例1-2】已知,,直线和垂直,则的最小值为( )
A.B.C.D.
【答案】B
【解析】,,直线,,且,
,即.
则,当且仅当时,等号成立,
故的最小值为8,
故选:B.
【方法技巧】
【解题方法总结】
判断两直线的位置关系可以从斜率是否存在分类判断,也可以按照以下方法判断:一般地,设(不全为0),(不全为0),则:
当时,直线相交;
当时,直线平行或重合,代回检验;
当时,直线垂直,与向量的平行与垂直类比记忆.
【变式1-1】直线与直线相交,则实数的值为( )
A.或B.或
C.且D.且
【答案】D
【解析】由直线与直线相交,得,
即,解得且,
所以实数k的值为且.
故选:D
【变式1-2】点为直线上不同的两点,则直线与直线的位置关系是( )
A.相交B.平行C.重合D.不确定
【答案】A
【解析】由点为直线上不同的两点,
则直线与直线的斜率存在时一定为,
可以把这两个斜率看成直线上两点到原点的斜率的倒数,
由已知可得,则,即两直线不可能平行与重合,则只能相交;
若直线与直线的斜率有一个不存在,则另一个斜率必存在,也能判定两直线相交;
故选:A.
【变式1-3】(2024·高三·广东·开学考试)已知直线,直线,则是的( )
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分又不必要条件
【答案】A
【解析】因为或,
所以是的充分不必要条件.
故选:A.
【变式1-4】(2024·高三·上海宝山·开学考试)已知集合,,则下列结论正确的是( )
A.存在,使得
B.当时,
C.当时,
D.对任意的,都有
【答案】D
【解析】对于A,表示过定点,且斜率不为的直线,
集合表示直线上所有的点,,A错误;
对于B,当时,,,
由得:,,B错误;
对于C,当时,,满足;
当,即时,直线与平行,
,解得:;
综上所述:当时,或,C错误;
对于D,若,则且直线与重合,
,方程组无解,,D正确.
故选:D.
题型二:两直线的交点与距离问题
【典例2-1】(2024·高三·江苏苏州·开学考试)已知直线与直线交于,则原点到直线距离的最大值为( )
A.2B.C.D.1
【答案】B
【解析】因为两直线交于,
则,即,且,则;
由原点到直线的距离
由,
则,当且仅当时,取最大值,此时.
即两直线重合时,原点到直线的距离最大.
故选:B.
【典例2-2】若直线与直线的交点在第一象限,则实数的取值范围是( )
A.B.C.D.
【答案】A
【解析】,即交点为,
因为交点在第一象限,所以.
故选:A
【方法技巧】
两点间的距离,点到直线的距离以及两平行直线间的距离的计算,特别注意点到直线距离公式的结构.
【变式2-1】已知点,,,则的面积为 .
【答案】5
【解析】设边上的高为,则就是点C到AB所在直线的距离.
易知.
由两点式可得边所在直线的方程为,即.
点到直线的距离,
所以的面积为.
故答案为:5
【变式2-2】已知平面上点和直线,点P到直线l的距离为d,则 .
【答案】/4.5
【解析】依题意,直线,而点,
所以.
故答案为:
【变式2-3】已知直线,则点到直线的距离的最大值为 .
【答案】
【解析】直线,即,
由,解得,,所以直线恒过定点,
当直线l与直线AP垂直时,点到直线的距离的最大,
最大值为,
所以点到直线的距离的最大值为,
故答案为:
【变式2-4】已知点,若直线l过点,且A、B到直线l的距离相等,则直线l的方程为 .
【答案】或
【解析】依题意,到直线的距离相等.
的中点为,
当过以及时,
直线的方程为.
直线的斜率为,
当直线过并与平行时,
直线的方程为.
综上所述,直线的方程为或.
故答案为:或
【变式2-5】,与直线平行,则直线与的距离为 .
【答案】
【解析】因为//,所以,解得,
, ,
由两平行直线的距离公式可得:,
故答案为:
【变式2-6】若恰有两组的实数对满足关系式,则符合题意的的值为 .
【答案】/
【解析】可以看成点到直线:的距离,
可以看成点到直线:的距离,
由已知可得,,:不过原点,
又由恰有两组的实数对满足关系式,
所以可以看成有且仅有两条直线满足,直线方程:,
所以满足题意的直线:
第一条是线段的垂直平分线,当:是的垂直平分线时,
因为,所以,符合题意;
第二条只能取自与直线平行的两条直线中的一条,且此时另一条直线过原点,
此时第二条直线的方程为,
所以此时,即,符合题意;
所以.
故答案为:.
【变式2-7】(2024·全国·模拟预测)已知直线和与x轴围成的三角形是等腰三角形,则k的取值不可能为( )
A.B.C.D.
【答案】D
【解析】令直线的倾斜角分别为,则,
当围成的等腰三角形底边在x轴上时,,;
当围成的等腰三角形底边在直线上时,或,
因为,且,解得,
所以,或;
当围成的等腰三角形底边在直线上时,,则.
故选:D.
题型三:有关距离的最值问题
【典例3-1】我国著名数学家华罗庚曾经说过:“数形结合百般好,隔离分家万事休.”事实上有很多代数问题可以转化为几何问题加以解决,根据上述观点,当取得最小值时,实数的值为( )
A.B.3C.D.4
【答案】C
【解析】,
表示平面上点与点,的距离和,
连接,与轴交于,此时直线方程为,
令,则
的最小值为,此时
故选:C.
【典例3-2】设,其中.则的最小值为( )
A.8B.9C.D.
【答案】B
【解析】设,则表示:,
,则直线的方程为,令,则,
所以直线与轴相交于点,
所以,
所以,当点P为时,等号成立,故的最小值为9.
故选:B.
【方法技巧】
数学结合,利用距离的几何意义进行转化.
【变式3-1】已知,,,为四个实数,且,,,则的最小值为( )
A.B.C.D.5
【答案】D
【解析】设,则,
所以
,
而可看做轴上动点与两定点的距离和,如图,
由图可知当运动到时,最小,最小值为,
所以的最小值为.
故选:D
【变式3-2】已知为直线上的一点,则的最小值为( )
A.B.C.4D.
【答案】A
【解析】如图,为点到原点和到点的距离之和,
即.设关于直线对称的点为,则得,即.
易得,当A,,三点共线时,取到最小值,且最小值为.
故选:A.
【变式3-3】的最小值为( )
A.B.C.D.
【答案】D
【解析】由题意知,
,
设,
则的几何意义为的值,
如图,作点关于x轴的对称点,连接,
与x轴的交点即为所求点P,此时取得最小值,为.
而,
即的最小值为,
所以的最小值为.
故选:D
【变式3-4】已知实数,满足,,,则的最小值是 .
【答案】/
【解析】依题意,方程、分别表示以原点为圆心,2、3为半径的圆,
令,即点分别在、上,如图,
显然,,即有,
,取线段中点,连接,则,
因此点在以原点为圆心,为半径的圆上,
而,
即表示点到直线的距离和的倍,
过分别作直线的垂线,垂足分别为,过作垂直于直线于点,
于是,,
,原点到直线的距离,
显然,当且仅当点共线,且点在线段上时取等号,
所以.
故答案为:
【变式3-5】已知点分别在直线与直线上,且,点,,则的最小值为 .
【答案】
【解析】易知,作出图象如下,过点作直线,则,
直线,过作直线,与直线交于点,易知四边形为平行四边形,
故,且到直线的距离等于到的距离,
设,则,解得或(舍,所以,
而,且(定值),
故只需求出的最小值即可,显然,
故的最小值为.
故答案为:.
【变式3-6】(多选题)已知两点,点是直线:上的动点,则下列结论中正确的是( )
A.存在使最小B.存在使最小
C.存在使最小D.存在使最小
【答案】ABD
【解析】对于A:设点关于直线的对称点为,所以,所以,所以,
所以,当且仅当为与交点时满足题意,
又因为,即,
所以,所以,所以,故A正确;
对于B:设,所以,
所以,当且仅当时有最小值,
此时,所以,故B正确;
对于C:如下图,根据与的位置关系可判断出有最大值,无最小值,故C错误;
对于D:因为,取等号时,即为垂直平分线与的交点,
因为垂直平分线方程为,即,
所以,所以,所以,故D正确;
故选:ABD.
【变式3-7】(多选题)已知直线和三点,,,过点C的直线与x轴、y轴的正半轴交于M,N两点.下列结论正确的是( )
A.P在直线l上,则的最小值为
B.直线l上一点使最大
C.当最小时的方程是
D.当最小时的方程是
【答案】BC
【解析】对于A:设点关于直线l的对称点为,
则,解得
,
当三点共线时取最小值.A错误;
对于B:,当三点共线时取最大值,
又,即,
联立,解得,
即直线l上一点使最大,B正确;
对于C:设,
当时,,当时,,
即,
,
当且仅当,即时等号成立,
此时,即,C正确;
对于D:,
当且仅当,即时等号成立,
此时,即,D错误.
故选:BC.
【变式3-8】已知点在直线,点在直线上,且,的最小值为( )
A.B.C.D.5
【答案】D
【解析】由已知表示点Mx1,y1到点的距离,
表示点Nx2,y2到点的距离,
所以,
过点作,垂足为,
因为直线的方程为,,
所以,
又直线与直线平行,,
所以,所以,
所以四边形为平行四边形,所以,
所以,
又,当且仅当三点共线时等号成立,
所以当点为线段与直线的交点时,
取最小值,最小值为,
因为过点与直线垂直的直线的方程为,
联立,可得,
所以点的坐标为,所以,
所以的最小值为,
故选:D.
【变式3-9】过定点A的动直线和过定点B的动直线交于点M,则的最大值是( )
A.B.3C.D.
【答案】C
【解析】由题意知过定点,
动直线即过定点,
对于直线和动直线满足,
故两直线垂直,
因此点M在以为直径的圆上,,
则,
所以,
当且仅当时等号成立,
故的最大值为,
故选:C
【变式3-10】已知,为实数,代数式的最小值是 .
【答案】10
【解析】设点,
则
,
当且仅当分别为连线与两坐标轴的交点时,等号成立.
故答案为:10.
题型四:点关于点对称
【典例4-1】直线l经过点,与x轴、y轴分别交于A,B两点,当P为AB中点时, .
【答案】
【解析】设Aa,0,,
∵P为AB中点,∴,
解得,,
即,,
所以
故答案为:.
【典例4-2】已知,,点是线段的中点,则 .
【答案】
【解析】由中点坐标公式知:,,解得:,,.
故答案为:.
【方法技巧】
求点关于点中心对称的点,由中点坐标公式得
【变式4-1】已知点在轴上,点在轴上,线段的中点的坐标为,则线段的长度为 .
【答案】
【解析】在平面直角坐标系中,,
则为直角三角形,且为斜边,
故.
故答案为:
【变式4-2】设点A在x轴上,点B在y轴上,的中点是,则等于
【答案】
【解析】根据点A在x轴上,点B在y轴上,且的中点是,利用中点坐标公式得到A,B的坐标,再利用两点间的距离公式求解.因为点A在x轴上,点B在y轴上,且的中点是,
所以,
所以,
故答案为:
【变式4-3】已知直线l与直线及直线分别交于点P,Q.若PQ的中点为点,则直线l的斜率为 .
【答案】
【解析】设,则.由点Q在直线上,得,.故.
所以直线l的斜率为,所以
故答案为
【变式4-4】已知直线与直线和的交点分别为,若点是线段的中点,则直线的方程为 .
【答案】
【解析】因为直线与直线和的交点分别为,
设,
因为点是线段的中点,由中点公式可得,
解得,所以直线的斜率为,
所以直线的方程为,即.
故答案为:.
题型五:点关于线对称
【典例5-1】将一张坐标纸对折,如果点与点重合,则点与点 重合.
【答案】
【解析】已知点与点,可知线段的中点为,
且,则线段的中垂线的斜率,
则线段的中垂线方程为,即,
设点关于直线的对称点为,
则,解得,
所以所求点为.
故答案为:.
【典例5-2】点关于直线对称的点的坐标为( )
A.B.C.D.
【答案】D
【解析】设所求对称点的坐标为,
则,解得,
故点关于直线对称的点的坐标为.
故选:D.
【方法技巧】
求点关于直线对称的点
方法一:(一中一垂),即线段的中点M在对称轴上,若直线的斜率存在,则直线的斜率与对称轴的斜率之积为-1,两个条件建立方程组解得点
方法二:先求经过点且垂直于对称轴的直线(法线),然后由得线段的中点,从而得
【变式5-1】若直线和直线关于直线对称,则直线恒过定点( )
A.B. C.D.
【答案】C
【解析】因为直线过定点,
点关于直线对称的点为,
故直线恒过定点.
故选:C
【变式5-2】一条光线从点射出,经直线反射后经过点,则反射光线所在直线的方程为( )
A.B.
C.D.
【答案】B
【解析】设点关于直线的对称点为,
则,化简得,解得,
故反射光线过点,
则反射光线所在直线的方程为.
故选:B.
【变式5-3】在等腰直角三角形ABC中,,点P是边AB上异于A,B的一点,光从点P出发经反射后又回到点P,反射点为Q,R,若光线QR经过的重心,则 .
【答案】
【解析】依题意,以点A为原点,直线AB为x轴,直线AC为y轴建立平面直角坐标系,如图,
则,,,的重心G的坐标为,
设点P的坐标为,,则点P关系y轴对称点,
设点P关于直线对称点,显然直线BC的方程为,
于是,解得,即点,
由光的反射定律知,光线过点,也过点,而光线经过的重心,因此点共线,
则有,整理得,解得,
所以.
故答案为:
题型六:线关于点对称
【典例6-1】直线关于点对称的直线方程为 .
【答案】
【解析】在直线上取点、,
点关于点的对称点为,点关于点的对称点为,
直线的斜率为,
所以,所求直线方程为,即.
故答案为:.
【典例6-2】直线关于点对称的直线方程为 .
【答案】
【解析】在对称直线上任取一点,设关于点对称的点为,由于在直线上,所以,即,
故答案为:
【方法技巧】
求直线l关于点中心对称的直线
求解方法是:在已知直线l上取一点关于点中心对称得,再利用,由点斜式方程求得直线的方程(或者由,且点到直线l及的距离相等来求解).
【变式6-1】直线关于点对称的直线的方程为 .
【答案】
【解析】设为上任意一点,则关于点的对称点为,
因为在直线l上,所以,即直线的方程为.
故答案为:
【变式6-2】直线恒过定点,则直线关于点对称的直线方程为 .
【答案】
【解析】由得:,当时,,;
设直线关于点对称的直线方程为,
,解得:或(舍),
直线关于点对称的直线方程为.
故答案为:.
【变式6-3】在平面直角坐标系xOy中,将直线l沿x轴正方向平移3个单位长度,沿y轴正方向平移5个单位长度,得到直线l1.再将直线l1沿x轴正方向平移1个单位长度,沿y轴负方向平移2个单位长度,又与直线l重合.若直线l与直线l1关于点(2,3)对称,则直线l的方程是 .
【答案】6x-8y+1=0
【解析】根据平移得到l1:y=k(x-3)+5+b和直线:y=kx+3-4k+b,解得k=,再根据对称解得b=,计算得到答案.由题意知直线l的斜率存在,设直线l的方程为y=kx+b,
则直线l1:y=k(x-3)+5+b,平移后的直线方程为y=k(x-3-1)+b+5-2
即y=kx+3-4k+b,∴b=3-4k+b,解得k= ,
∴直线l的方程为y=x+b,直线l1为y=x++b
取直线l上的一点 ,则点P关于点(2,3)的对称点为 ,
,解得b=.
∴直线l的方程是 ,即6x-8y+1=0.
故答案为:6x-8y+1=0
题型七:线关于线对称
【典例7-1】若直线与直线关于直线对称,则直线的一般式方程为 .
【答案】
【解析】设直线上任意一点,则点关于直线对称点,
因为直线与直线关于直线对称,所以在直线上,
即,得到直线的一般式方程为
故答案为:
【典例7-2】直线与直线关于直线对称,则直线的倾斜角是 .
【答案】
【解析】直线,故直线的斜率等于,
设直线的倾斜角等于,则,
且,故,
同理直线的倾斜角为,
所以直线与直线关于直线对称,则直线的倾斜角是.
故答案为:.
【方法技巧】
求直线l关于直线对称的直线
若直线,则,且对称轴与直线l及之间的距离相等.
此时分别为,由,求得,从而得.
若直线l与不平行,则.在直线l上取异于Q的一点,然后求得关于直线对称的点,再由两点确定直线(其中).
【变式7-1】已知直线,直线,若直线关于直线l的对称直线为,则直线的方程为 .
【答案】.
【解析】由题意知,设直线,在直线上取点,
设点关于直线的对称点为,
则, 解得,即,
将代入的方程得,
所以直线的方程为.
故答案为:
【变式7-2】若直线l与直线的夹角平分线为,则直线l的方程为 .
【答案】
【解析】由题意可得直线l与直线关于直线对称,
由于直线上的任意一点关于直线的对称点为,
因为已知直线,则的方程是,即,
故答案为:.
【变式7-3】直线:关于直线:的对称直线方程为 .
【答案】
【解析】设直线关于直线对称的直线为,由,解得,
则点在直线上;
在直线上取一点,设其关于直线对称的点为,
则,解得,即,
所以直线的方程为,即.
故答案为:
【变式7-4】直线关于直线的对称直线的方程为 .
【答案】
【解析】设为所求直线上一点,它关于的对称点为,
则可得,
由题可得在直线上,
所以,整理可得所求的对称直线方程为.
故答案为:.
题型八:直线系方程
【典例8-1】过两直线和的交点且过原点的直线方程为 .
【答案】
【解析】令所求直线为,
又直线过原点,则,
所以所求直线为.
故答案为:
【典例8-2】经过点和两直线;交点的直线方程为 .
【答案】
【解析】设所求直线方程为,
点在直线上,
,
解得,
所求直线方程为,即.
故答案为:.
【方法技巧】
利用直线系方程求解.
【变式8-1】已知两直线和的交点为,则过两点的直线方程为 .
【答案】
【解析】依题意两直线和的交点为,
所以在直线上,
所以过两点所在直线方程为.
故答案为:
【变式8-2】设直线经过和的交点,且与两坐标轴围成等腰直角三角形,则直线的方程为 .
【答案】或
【解析】方法一:由,得,
所以两条直线的交点坐标为(14,10),
由题意可得直线的斜率为1或-1,
所以直线的方程为或,
即或.
方法二:设直线的方程为,整理得,
由题意,得,解得或,
所以直线的方程为或.
故答案为:或.
【变式8-3】已知直线的方程为,求坐标原点到的距离的最大值 .
【答案】
【解析】直线的方程为,即
令,解得:
所以直线恒过定点,
所以原点到直线的距离,即到直线的距离的最大值为.
故答案为:.
1.(2021年全国新高考II卷数学试题)抛物线的焦点到直线的距离为,则( )
A.1B.2C.D.4
【答案】B
【解析】抛物线的焦点坐标为,
其到直线的距离:,
解得:(舍去).
故选:B.
2.(2021年全国高考甲卷数学(文)试题)点到双曲线的一条渐近线的距离为( )
A.B.C.D.
【答案】A
【解析】由题意可知,双曲线的渐近线方程为:,即,
结合对称性,不妨考虑点到直线的距离:.
故选:A.
3.(2020年全国统一高考数学试卷(文科)(新课标Ⅲ))点(0,﹣1)到直线距离的最大值为( )
A.1B.C.D.2
【答案】B
【解析】由可知直线过定点,设,
当直线与垂直时,点到直线距离最大,
即为.
故选:B.
1.已知点和,点P在x轴上,且为直角,求点P的坐标.
【答案】或.
【解析】设,因为,
所以由勾股定理可得,
即,解得或,所以点的坐标是或.
故答案为:或.
2.已知四边形ABCD的四个顶点是,,,,求证:四边形ABCD为矩形.
【解析】因为四个点的横坐标各不相等,所以四边形四条边所在直线的斜率都存在,
所以,,,,
所以,,,
所以四边形四条边两两垂直,所以四边形四个内角都为,
所以四边形是矩形.
3.如图,已知直线与直线,在上任取一点A,在上任取一点B,连接AB,取AB的靠近点A的三等分点C,过点C作的平行线,求与间的距离.
【解析】过A做于D,交于E,如图所示:
因为,且由题意得,
所以,所以,
又直线与间的距离,
所以求与间的距离.
4.三条直线,与相交于一点,求a的值.
【解析】解方程组,得,
∴交点坐标为:(4,﹣2),
代入直线ax+2y+8=0,得4a﹣4+8=0,
∴a=﹣1.
5.已知AO是边BC的中线,用坐标法证明.
【解析】取BC边所在直线为x轴,BC的垂直平分线为y轴,建立直角坐标系,如图
设,(其中),则
,
所以,即证.
6.已知,.
(1)求证:,并求使等式成立的条件.
(2)说明上述不等式的几何意义.
【解析】(1)证明:∵0<x<1,0<y<1,设P(x,y),A(1,0),B(1,1),C(0,1),如图:
则|PO|,|PA|,|PB|,|PC|,
∵|PO|+|PB|≥|BO|,|PA|+|PC|≥|AC|
∴|PO|+|PB|+|PA|+|PC|≥ (当且仅当点P为正方形的对角线AC与OB的交点是取等号),
即x=y时取等号.
∴.
(2)对于(1)中不等式,它的几何意义是:边长为1的正方形内任意一点到四个顶点的距离的和不小于两条对角线的和.
7.已知为任意实数,当变化时,方程表示什么图形?图形有何特点?
【解析】因为方程化简得:
为任意实数,方程表示直线.
因为,
所以当,直线恒成立,
故直线过定点.
易错点:两平行直线间的距离公式应用错误
易错分析: 应用两平行直线间的距离公式一定要注意两平行直线的方程对应x,y的系数相等时,才可利用两平行线间的距离公式求解.
【易错题1】,与直线平行,则直线与的距离为 .
【答案】
【解析】因为//,所以,解得,
, ,
由两平行直线的距离公式可得:,
故答案为:
【易错题2】两平行直线与之间的距离为 .
【答案】/
【解析】由,可得,
所以与之间的距离为.
故答案为:.
答题模板:已知两直线平行或垂直求参数
1、模板解决思路
当需要通过两直线的平行或垂直关系来求解参数的值时,一般的做法是首先考察这两条直线的斜率。
如果两条直线平行,那么它们的斜率相等;如果两条直线垂直,那么它们的斜率之积为-1。
这里需要特别注意,当直线垂直于x轴时,斜率不存在,此时应单独考虑。
2、模板解决步骤
第一步:将两条直线的方程均化成斜截式.
第二步:根据两直线平行或垂直,列出方程(组).
第三步:解方程(组),求出参数的值,由两直线平行求参数后要检验两直线是否重合.
【典型例题1】已知直线,若,则 .
【答案】0
【解析】①当时,②当时,若,可得与重合,不合题意.故.
故答案为:.
【典型例题2】已知直线和垂直且,则的最小值为 .
【答案】
【解析】由题意得,故,
因为,由基本不等式得
,
当且仅当,即时,等号成立.
故答案为:
考点要求
考题统计
考情分析
(1)两条直线的平行与垂直
(2)两直线的交点与距离问题
2022年上海卷第7题,5分
2020年III卷第8题,5分
2020年上海卷第7题,5分
高考对两条直线的位置关系的考查比较稳定,考查内容、频率、题型难度均变化不大,备考时应熟练掌握两条直线的位置关系、距离公式、对称问题等,特别要重视两条直线的位置关系以及点到直线的距离公式这两个考点.
复习目标:
(1)能根据斜率判定两条直线平行或垂直.
(2)能用解方程组的方法求两条直线的交点坐标.
(3)掌握平面上两点间的距离公式、点到直线的距离公式,会求两条平行直线间的距离.
两直线方程
平行
垂直
(斜率存在)
(斜率不存在)
或
或中有一个为0,另一个不存在.
相关试卷
这是一份第05讲 古典概型与概率的基本性质(八大题型)(讲义)-2025年高考数学一轮复习讲练测(新教材新高考),文件包含第05讲古典概型与概率的基本性质八大题型讲义原卷版docx、第05讲古典概型与概率的基本性质八大题型讲义解析版docx等2份试卷配套教学资源,其中试卷共53页, 欢迎下载使用。
这是一份第02讲 排列、组合(十九大题型)(讲义)-2025年高考数学一轮复习讲练测(新教材新高考),文件包含第02讲排列组合十九大题型讲义原卷版docx、第02讲排列组合十九大题型讲义解析版docx等2份试卷配套教学资源,其中试卷共90页, 欢迎下载使用。
这是一份新高考数学一轮复习讲练测第8章第02讲 两条直线的位置关系(八大题型)(讲义)(2份打包,原卷版+解析版),文件包含新高考数学一轮复习讲练测第8章第02讲两条直线的位置关系八大题型讲义原卷版doc、新高考数学一轮复习讲练测第8章第02讲两条直线的位置关系八大题型讲义解析版doc等2份试卷配套教学资源,其中试卷共0页, 欢迎下载使用。












