



第02讲 两条直线的位置关系(八大题型)(讲义)-2024年高考数学一轮复习讲义(新教材新高考)
展开2、精练习题。复习时不要搞“题海战术”,应在老师的指导下,选一些源于课本的变式题,或体现基本概念、基本方法的基本题,通过解题来提高思维能力和解题技巧,加深对所学知识的深入理解。在解题时,要独立思考,一题多思,一题多解,反复玩味,悟出道理。
3、加强审题的规范性。每每大考过后,总有同学抱怨没考好,纠其原因是考试时没有注意审题。审题决定了成功与否,不解决这个问题势必影响到高考的成败。那么怎么审题呢? 应找出题目中的已知条件 ;善于挖掘题目中的隐含条件 ;认真分析条件与目标的联系,确定解题思路 。
4、重视错题。错误是最好的老师”,但更重要的是寻找错因,及时进行总结,三五个字,一两句话都行,言简意赅,切中要害,以利于吸取教训,力求相同的错误不犯第二次。
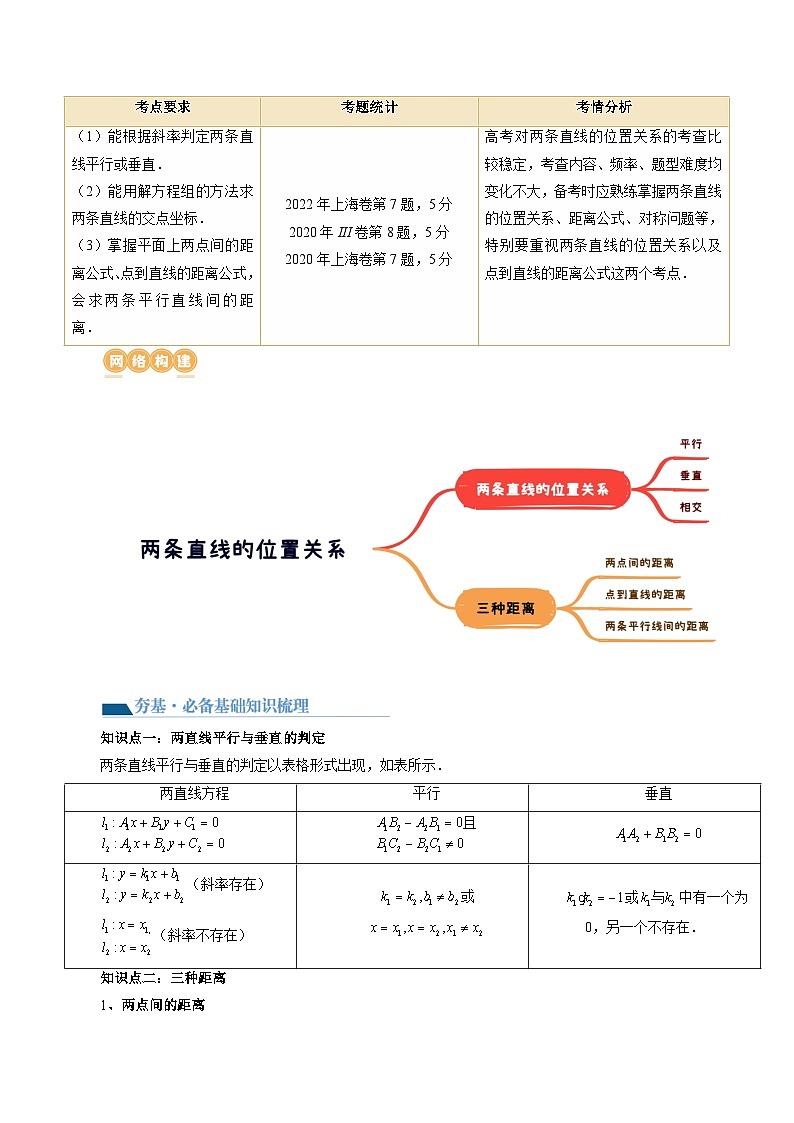
第02讲 两条直线的位置关系
目录
知识点一:两直线平行与垂直的判定
两条直线平行与垂直的判定以表格形式出现,如表所示.
知识点二:三种距离
1、两点间的距离
平面上两点的距离公式为.
特别地,原点O(0,0)与任一点P(x,y)的距离
2、点到直线的距离
点到直线的距离
特别地,若直线为l:x=m,则点到l的距离;若直线为l:y=n,则点到l的距离
3、两条平行线间的距离
已知是两条平行线,求间距离的方法:
(1)转化为其中一条直线上的特殊点到另一条直线的距离.
(2)设,则与之间的距离
注:两平行直线方程中,x,y前面对应系数要相等.
4、双根式
双根式型函数求解,首先想到两点间的距离,或者利用单调性求解.
【解题方法总结】
1、点关于点对称
点关于点对称的本质是中点坐标公式:设点关于点的对称点为,则根据中点坐标公式,有
可得对称点的坐标为
2、点关于直线对称
点关于直线对称的点为,连接,交于点,则垂直平分,所以,且为中点,又因为在直线上,故可得,解出即可.
3、直线关于点对称
法一:在已知直线上取两点,利用中点坐标公式求出它们关于已知点对称的两点坐标,再由两点式求出直线方程;
法二:求出一个对称点,再利用两对称直线平行,由点斜式得到所求直线方程.
4、直线关于直线对称
求直线,关于直线(两直线不平行)的对称直线
第一步:联立算出交点
第二步:在上任找一点(非交点),利用点关于直线对称的秒杀公式算出对称点
第三步:利用两点式写出方程
5、常见的一些特殊的对称
点关于轴的对称点为,关于轴的对称点为.
点关于直线的对称点为,关于直线的对称点为.
点关于直线的对称点为,关于直线的对称点为.
点关于点的对称点为.
点关于直线的对称点为,关于直线的对称点为.
6、过定点直线系
过已知点的直线系方程(为参数).
7、斜率为定值直线系
斜率为的直线系方程(是参数).
8、平行直线系
与已知直线平行的直线系方程(为参数).
9、垂直直线系
与已知直线垂直的直线系方程(为参数).
10、过两直线交点的直线系
过直线与的交点的直线系方程:(为参数).
题型一:两直线位置关系的判定
例1.(2023·高二课时练习)直线与互相垂直,则这两条直线的交点坐标为( )
A.B.
C.D.
【答案】C
【解析】易知直线的斜率为,
由两直线垂直条件得直线的斜率,解得;
联立,解得;
即交点为
故选:C.
例2.(2023·江苏南通·高二江苏省如皋中学校考开学考试)已知过点和点的直线为l1,. 若,则的值为( )
A.B.
C.0D.8
【答案】A
【解析】因为,所以,解得,又,所以,
解得.所以.
故选:A.
例3.(2023·浙江温州·高二乐清市知临中学校考开学考试)设直线,,则是的( )
A.充要条件B.必要不充分条件
C.充分不必要条件D.既不充分也不必要条件
【答案】C
【解析】当时,直线,,
此时,则,所以,故充分性成立;
当时,,解得或,故必要性不成立;
所以“”是“”的充分不必要条件,
故选:C.
变式1.(2023·广东东莞·高三校考阶段练习)直线:与直线:平行, 则( )
A.或B.C.D.
【答案】A
【解析】因为直线:与直线:平行,
所以或,
当时,直线:,直线:,
此时直线与直线平行,满足题意,
当时,直线:,直线:,
此时直线与直线平行,满足题意,
故选:A.
变式2.(2023·全国·高三专题练习)已知直线:,:,则条件“”是“”的( )
A.充分必要条件B.充分不必要条件
C.必要不充分条件D.既不必要也不充分条件
【答案】B
【解析】若,则,
解得或.
故是的充分不必要条件.
故选:B
变式3.(2023·黑龙江牡丹江·牡丹江一中校考三模)已知直线,若,则( )
A.B.0C.1D.2
【答案】B
【解析】因为直线,且,则,
所以.
故选:B
变式4.(2023·全国·高三专题练习)已知A(-1,2),B(1,3),C(0,-2),点D使AD⊥BC,AB∥CD,则点D的坐标为( )
A.B.
C.D.
【答案】D
【解析】设D(x,y),∵AD⊥BC,∴·=-1,∴x+5y-9=0,
∵AB∥CD,∴=,∴x-2y-4=0,由得,,
故选:D.
变式5.(2023·甘肃陇南·高三统考期中)已知的顶点,,其垂心为,则其顶点的坐标为
A.B.C.D.
【答案】A
【解析】为的垂心 ,
又,
直线斜率存在且,
设,则,解得:
本题正确选项:
变式6.(2023·全国·高三专题练习)直线,直线,下列说法正确的是( )
A.,使得B.,使得
C.,与都相交D.,使得原点到的距离为3
【答案】B
【解析】对A,要使,则,所以,解之得,此时与重合,选项A错误;
对B,要使,,,解之得,所以B正确;
对C,过定点,该定点在上,但是当时,与重合,所以C错误;
对D,,化简得,此方程,无实数解,所以D错误.
故选:B.
变式7.(2023·全国·高三对口高考)设分别为中所对边的边长,则直线与直线的位置关系是( )
A.相交但不垂直B.垂直C.平行D.重合
【答案】B
【解析】由题意可知直线与直线的斜率均存在且不为0,
直线的斜率,
直线的斜率,
由正弦定理可得,
所以两直线垂直,
故选:B
【解题方法总结】
判断两直线的位置关系可以从斜率是否存在分类判断,也可以按照以下方法判断:一般地,设(不全为0),(不全为0),则:
当时,直线相交;
当时,直线平行或重合,代回检验;
当时,直线垂直,与向量的平行与垂直类比记忆.
题型二:两直线的交点与距离问题
例4.(2023·全国·高三专题练习)若直线与直线的交点位于第一象限,则直线l的倾斜角的取值范围是( )
A.B.
C.D.
【答案】D
【解析】法一:联立两直线方程,得,解得,
所以两直线的交点坐标为.
因为两直线的交点在第一象限,所以,解得,
设直线l的倾斜角为θ,则,又,所以.
法二:由题意,直线l过定点,
设直线与x轴、y轴的交点分别为.
如图,当直线l在阴影部分(不含边界)运动时,两直线的交点在第一象限,易知,
∴的倾斜角为,的倾斜角为.
∴直线l的倾斜角的取值范围是.
故选:D
例5.(2023·上海浦东新·华师大二附中校考三模)已知三条直线,,将平面分为六个部分,则满足条件的的值共有( )
A.个B.2个C.个D.无数个
【答案】C
【解析】当三条直线交于一点时,可将平面分为六个部分,
联立与,解得,
则将代入中,,解得,
当与平行时,满足要求,此时,
当与平行时,满足要求,此时,
综上,满足条件的的值共有3个.
故选:C
例6.(2023·全国·高三专题练习)若三条直线不能围成三角形,则实数的取值最多有( )
A.个B.个
C.个D.个
【答案】C
【解析】三条直线不能构成三角形 至少有两条直线平行或三条直线相交于同一点.
若∥,则;若∥,则;
若∥,则的值不存在;
若三条直线相交于同一点,
直线和联立:,直线和交点为;
直线和联立:,直线和交点为;
三条直线相交于同一点两点重合或.
故实数的取值最多有个.
故选:C
变式8.(2023·江苏宿迁·高二泗阳县实验高级中学校考阶段练习)若点在直线上,O是原点,则OP的最小值为( )
A.B.2C.D.4
【答案】C
【解析】由题意可知,OP的最小值即为原点到直线的距离,
则.
故选:C
变式9.(2023·吉林长春·高二东北师大附中校考期中)已知点在直线上,则的最小值为( )
A.1B.2C.3D.4
【答案】B
【解析】就是到原点距离,
到原点距离的最小值为
则的最小值为2,
故选:B.
变式10.(2023·高二课时练习)已知点、、,且,则 .
【答案】
【解析】已知点、、,且,
则,解得.
故答案为:.
变式11.(2023·全国·高二专题练习)已知点与点间的距离为,则 .
【答案】9或
【解析】由,
得,
即,解得或.
故答案为:9或.
变式12.(2023·全国·高二课堂例题)已知点,,,则的面积为 .
【答案】5
【解析】设边上的高为,则就是点C到AB所在直线的距离.
易知.
由两点式可得边所在直线的方程为,即.
点到直线的距离,
所以的面积为.
故答案为:5
变式13.(2023·江苏淮安·高二统考期中)已知平面上点和直线,点P到直线l的距离为d,则 .
【答案】/4.5
【解析】依题意,直线,而点,
所以.
故答案为:
变式14.(2023·黑龙江哈尔滨·高三哈尔滨七十三中校考期中)点到直线的距离的最大值是 .
【答案】
【解析】因为直线恒过点,
记,直线为直线,
则当时,此时点到直线的距离最大,
∴点到直线距离的最大值为:
.
故答案为:.
变式15.(2023·高二课时练习)过直线与直线的交点,且到点的距离为1的直线l的方程为 .
【答案】或
【解析】解析:由解得
所以l1,l2的交点为.
显然,直线满足条件;
当直线斜率存在时,设直线方程为,
即,
依题意有,解得.
所以所求直线方程为或.
故答案为:或.
变式16.(2023·江西新余·高二校考开学考试)若点到直线的距离为3,则 .
【答案】
【解析】因为点到直线的距离为3,
可得,即,解得或,
又因为,所以.
故答案为:.
变式17.(2023·全国·高三专题练习)点,到直线l的距离分别为1和4,写出一个满足条件的直线l的方程: .
【答案】或或(填其中一个即可)
【解析】设,,连接MN,则.
以M为圆心,1为半径作圆M,以N为圆心4为半径作圆N,则两圆外切,
所以两圆有3条公切线,即符合条件的直线l有3条.
当公切线的斜率不存在时,显然公切线的方程为.
当公切线的斜率存在时,设公切线的方程为,则有,
由①②得,所以或.
由①及得,由①及得,
所以公切线方程为或.
综上,直线l的方程为或或.
故答案为:或或
变式18.(2023·浙江温州·高二乐清市知临中学校考开学考试)若两条直线与平行,则与间的距离是 .
【答案】/
【解析】两条直线与平行,
解得,
经检验时,,两直线不重合;
所以,
则与间的距离,
故答案为:.
变式19.(2023·江苏宿迁·高二泗阳县实验高级中学校考阶段练习)平行直线与之间的距离为 .
【答案】/0.3
【解析】由题意得即
则平行直线与之间的距离为,
故答案为:
变式20.(2023·新疆·高二校联考期末)已知不过原点的直线与直线平行,且直线与的距离为,则直线的一般式方程为 .
【答案】
【解析】直线不过原点且与平行,可设直线,
与之间的距离,解得:或(舍),
直线的一般式方程为:.
故答案为:.
【解题方法总结】
两点间的距离,点到直线的距离以及两平行直线间的距离的计算,特别注意点到直线距离公式的结构.
题型三:有关距离的最值问题
例7.(2023·北京·高三强基计划)的最小值所属区间为( )
A.B.
C.D.前三个答案都不对
【答案】C
【解析】如图,设.
根据题意,设题中代数式为M,则,
等号当P,Q分别为直线与x轴,y轴交点时取得.
因此所求最小值为13.
故选:C.
例8.(2023·全国·高三专题练习)已知实数,满足,,,则的最小值是 .
【答案】/
【解析】依题意,方程、分别表示以原点为圆心,2、3为半径的圆,
令,即点分别在、上,如图,
显然,,即有,
,取线段中点,连接,则,
因此点在以原点为圆心,为半径的圆上,
而,
即表示点到直线的距离和的倍,
过分别作直线的垂线,垂足分别为,过作垂直于直线于点,
于是,,
,原点到直线的距离,
显然,当且仅当点共线,且点在线段上时取等号,
所以.
故答案为:
例9.(2023·全国·高三专题练习)如图,平面上两点,在直线上取两点使,且使的值取最小,则的坐标为 .
【答案】
【解析】关于直线的对称点为,则有.过作平行于的直线为,由得,即此时直线为.过作,则,则.由于是常数,要使的值取最小,则的值取最小,即三点共线时最小.设,由得,即,解得(舍去.),即.设,则,解得,即,设,.由得,得,解得或(舍去),故.
故答案为:.
变式21.(2023·全国·高二专题练习)已知点分别在直线与直线上,且,点,,则的最小值为 .
【答案】
【解析】易知,作出图象如下,过点作直线,则,
直线,过作直线,与直线交于点,易知四边形为平行四边形,
故,且到直线的距离等于到的距离,
设,则,解得或(舍,所以,
而,且(定值),
故只需求出的最小值即可,显然,
故的最小值为.
故答案为:.
变式22.(2023·全国·高二课堂例题)已知直线过定点M,点在直线上,则的最小值是( )
A.5B.C.D.
【答案】B
【解析】由得,所以直线l过定点,
依题意可知的最小值就是点M到直线的距离,
由点到直线的距离公式可得.
故选:B.
变式23.(2023·全国·高三专题练习)著名数学家华罗庚曾说过:“数形结合百般好,割裂分家万事休.”事实上,有很多代数问题可以转化为几何问题加以解决,如:可以转化为点到点的距离,则的最小值为( ).
A.3B.C.D.
【答案】D
【解析】,
可以看作点到点的距离之和,
作点关于轴的对称点,显然当三点共线时,取到最小值,
最小值为间的距离.
故选:D.
变式24.(2023·贵州·校联考模拟预测)已知,满足,则的最小值为( )
A.B.C.1D.
【答案】B
【解析】
如图,过点作点关于线段的对称点,则.
设,则有,解得,所以.
设,则,所以,
又,所以点到轴的距离为,
所以,可视为线段上的点到轴的距离和到的距离之和.
过作轴,显然有,当且仅当三点共线时,和有最小值.
过点作轴,则即为最小值,与线段的交点,即为最小值时的位置.
因为,所以的最小值为.
故选:B.
变式25.(2023·江西·高三校联考阶段练习)在平面直角坐标系中,已知点,点为直线上一动点,则的最小值是( )
A.B.4C.5D.6
【答案】B
【解析】设点关于直线的对称点为,
则,解得,
所以,
所以,
当且仅当点为线段与直线的交点时等号成立,
所以的最小值是4,
故选:B.
变式26.(2023·高二课时练习)已知点,点P在x轴上使最大,求点P的坐标.
【解析】点关于x轴的对称点为,如图所示,若点不在直线上则,
连接并延长交x轴于点P,即为最大值.
直线的方程是,
即.
令,得.
则点P的坐标是.
变式27.(2023·天津和平·高二天津市汇文中学校考阶段练习)在直线上求一点P,使得:
(1)P到和的距离之差最大;
(2)P到和的距离之和最小.
【解析】(1)画出直线和点和,如图:在两侧,
作B关于直线的对称点,连接,
则直线和直线l的交点即为P,
设D为l上异于P的一点,则 ,
故,
故最大,即此时P到和的距离之差最大,
设,则 ,解得 ,
故直线方程为,联立 ,解得 ,
即;
(2)如图:在同侧,
作C关于直线的对称点,连接,
则直线和直线l的交点即为P,
设E为l上异于P的一点,则 ,
故,
故最小,即此时P到和的距离之和最小.,
设,则 ,解得 ,
故直线方程为,联立 ,解得 ,
即即;
变式28.(2023·全国·高三专题练习)已知函数的图象恒过定点A,圆上的两点,满足,则的最小值为( )
A.B.
C.D.
【答案】C
【解析】由题可知A为(0,1),且P、A、Q三点共线,
设弦PQ的中点为E(x,y),连接OE,则OE⊥PQ,即OE⊥AE,
∴,由此可得E的轨迹方程为,
即E的轨迹是以为圆心,为半径的圆,
设直线l为,
则E到l的最小距离为.
过P、E、Q分别作直线l的垂线,垂足分别为M、R、N,
则四边形MNQP是直角梯形,且R是MN的中点, 则ER是直角梯形的中位线,
∴,
即,
即.
故选:C.
变式29.(2023·江西·高三校联考开学考试)费马点是指三角形内到三角形三个顶点距离之和最小的点.当三角形三个内角均小于120°时,费马点与三个顶点连线正好三等分费马点所在的周角,即该点所对的三角形三边的张角相等且均为120°.根据以上性质,.则的最小值为( )
A.4B.C.D.
【答案】B
【解析】由题意得:的几何意义为点到点的距离之和的最小值,
因为,,
,
所以,故三角形ABC为等腰直角三角形,,
取的中点,连接,与交于点,连接,故,,
因为,所以,故,则,
故点到三角形三个顶点距离之和最小,即取得最小值,
因为,所以,同理得:,,
,
故的最小值为.
故选:B
变式30.(2023·全国·高三专题练习)已知,则的最小值为( )
A.B.C.D.
【答案】C
【解析】设点为直线上的动点,
由可看作与的距离和与的距离之和,
设点则点为点关于直线的对称点,
故,且,
所以,
当且仅当三点共线时,取等号,
所以的最小值为.
故选:C
变式31.(2023·陕西西安·高二西安市铁一中学校考期末)设,过定点的动直线和过定点的动直线交于点,则的最大值是( )
A.B.C.5D.10
【答案】C
【解析】
显然过定点,直线可化成,则经过定点,
根据两条直线垂直的一般式方程的条件,,
于是直线和直线垂直,又为两条直线的交点,则,
又,由勾股定理和基本不等式,
,则,
当时,的最大值是.
故选:C
变式32.(2023·全国·高二专题练习)过定点A的动直线和过定点B的动直线交于点M,则的最大值是( )
A.B.3C.D.
【答案】C
【解析】由题意知过定点,
动直线即过定点,
对于直线和动直线满足,
故两直线垂直,
因此点M在以为直径的圆上,,
则,
所以,
当且仅当时等号成立,
故的最大值为,
故选:C
【解题方法总结】
数学结合,利用距离的几何意义进行转化.
题型四:点点对称
例10.(2023·全国·高三专题练习)已知,,点是线段的中点,则 .
【答案】
【解析】由中点坐标公式知:,,解得:,,.
故答案为:.
例11.(2023·江苏南通·高二统考期中)已知点在轴上,点在轴上,线段的中点的坐标为,则线段的长度为 .
【答案】
【解析】在平面直角坐标系中,,
则为直角三角形,且为斜边,
故.
故答案为:
例12.(2023·高二课时练习)设点A在x轴上,点B在y轴上,的中点是,则等于
【答案】
【解析】根据点A在x轴上,点B在y轴上,且的中点是,利用中点坐标公式得到A,B的坐标,再利用两点间的距离公式求解.因为点A在x轴上,点B在y轴上,且的中点是,
所以,
所以,
故答案为:
变式33.(2023·高一课时练习)已知直线l与直线及直线分别交于点P,Q.若PQ的中点为点,则直线l的斜率为 .
【答案】
【解析】设,则.由点Q在直线上,得,.故.
所以直线l的斜率为,所以
故答案为
【解题方法总结】
求点关于点中心对称的点,由中点坐标公式得
题型五:点线对称
例13.(2023·湖南长沙·高一周南中学校考开学考试)如下图,一次函数的图象与轴,轴分别交于点,,点是轴上一点,点,分别为直线和轴上的两个动点,当周长最小时,点,的坐标分别为( )
A.,B.,
C.,D.,
【答案】C
【解析】作关于轴的对称点,
作关于的对称点,
连接交轴于,交于,所以,
此时周长最小,即,
由,直线方程为,所以,解得,
所以,可得直线方程为,即,
由,解得,所以,
令可,所以.
故选:C.
例14.(2023·全国·高二专题练习)若直线和直线关于直线对称,则直线恒过定点( )
A.B. C.D.
【答案】C
【解析】因为直线过定点,
点关于直线对称的点为,
故直线恒过定点.
故选:C
例15.(2023·全国·高二假期作业)抛物线的焦点关于直线的对称点的坐标是( )
A.B.C.D.
【答案】A
【解析】抛物线即,其焦点坐标为,
设关于直线的对称点的坐标是,
则,解得,则,
故选:A.
变式34.(2023·江西·高二校联考开学考试)如图,一束光线从出发,经过坐标轴反射两次经过点,则总路径长即总长为( )
A.B.6C.D.
【答案】C
【解析】设点关于轴的对称点为点,点关于轴的对称点为点,
由光线反射知识可得三点共线,三点共线,
故四点共线,
因为点的坐标为,点的坐标为,
所以点的坐标为,点的坐标为,
由对称的性质可得,
所以,
又,
所以.
故选:C.
变式35.(2023·四川遂宁·高二统考期末)已知点A与点关于直线对称,则点A的坐标为( )
A.B.
C.D.
【答案】C
【解析】设,因点A与点B关于直线对称,则AB中点在直线上且直线AB与直线垂直,
则,
即点A坐标为.
故选:C
变式36.(2023·湖北·高二校联考阶段练习)在等腰直角三角形中,,点是边上异于的一点,光线从点出发,经反射后又回到点,如图,若光线经过的重心,则( )
A.B.C.1D.2
【答案】C
【解析】根据题意,建立如图所示的坐标系,可得,,
故直线的方程为,
又由,,,则 的重心为,
设,其中,点关于直线 的对称点,则有,
解得,即,
易得关于 轴的对称点,
由光的反射原理可知,,,四点共成直线的斜率,
故直线的方程为,
由于直线过 的重心,代入化简可得,
解得:或 舍,即,故,
故选:C.
【解题方法总结】
求点关于直线对称的点
方法一:(一中一垂),即线段的中点M在对称轴上,若直线的斜率存在,则直线的斜率与对称轴的斜率之积为-1,两个条件建立方程组解得点
方法二:先求经过点且垂直于对称轴的直线(法线),然后由得线段的中点,从而得
题型六:线点对称
例16.(2023·高二课时练习)直线关于点对称的直线的方程为 .
【答案】
【解析】设为上任意一点,则关于点的对称点为,
因为在直线l上,所以,即直线的方程为.
故答案为:
例17.(2023·全国·高二专题练习)直线关于点的对称直线方程是 .
【答案】
【解析】设对称直线为,
则有,即
解这个方程得(舍)或.
所以对称直线的方程中.
故答案为:.
例18.(2023·河北廊坊·高三校考阶段练习)与直线关于点对称的直线的方程为 .
【答案】
【解析】直线关于点对称的直线的方程可设为,其中
又点到直线与到直线的距离相等
所以,即,所以或(舍).
故所求直线方程为:.
故答案为:.
变式37.(2023·全国·高三专题练习)直线恒过定点,则直线关于点对称的直线方程为 .
【答案】
【解析】由得:,当时,,;
设直线关于点对称的直线方程为,
,解得:或(舍),
直线关于点对称的直线方程为.
故答案为:.
变式38.(2023·辽宁营口·高三统考期末)若直线:与直线关于点对称,则当经过点时,点到直线的距离为 .
【答案】
【解析】因为直线恒过定点,
所以关于点对称,
所以关于点的对称点为,
此时和都在直线上,
由直线方程的两点式可得,即,
所以点到直线的距离为.
故答案为:.
变式39.(2023·全国·高三专题练习)在平面直角坐标系xOy中,将直线l沿x轴正方向平移3个单位长度,沿y轴正方向平移5个单位长度,得到直线l1.再将直线l1沿x轴正方向平移1个单位长度,沿y轴负方向平移2个单位长度,又与直线l重合.若直线l与直线l1关于点(2,3)对称,则直线l的方程是 .
【答案】6x-8y+1=0
【解析】根据平移得到l1:y=k(x-3)+5+b和直线:y=kx+3-4k+b,解得k=,再根据对称解得b=,计算得到答案.由题意知直线l的斜率存在,设直线l的方程为y=kx+b,
则直线l1:y=k(x-3)+5+b,平移后的直线方程为y=k(x-3-1)+b+5-2
即y=kx+3-4k+b,∴b=3-4k+b,解得k= ,
∴直线l的方程为y=x+b,直线l1为y=x++b
取直线l上的一点 ,则点P关于点(2,3)的对称点为 ,
,解得b=.
∴直线l的方程是 ,即6x-8y+1=0.
故答案为:6x-8y+1=0
【解题方法总结】
求直线l关于点中心对称的直线
求解方法是:在已知直线l上取一点关于点中心对称得,再利用,由点斜式方程求得直线的方程(或者由,且点到直线l及的距离相等来求解).
题型七:线线对称
例19.(2023·全国·高三专题练习)已知直线,直线,若直线关于直线l的对称直线为,则直线的方程为 .
【答案】.
【解析】由题意知,设直线,在直线上取点,
设点关于直线的对称点为,
则, 解得,即,
将代入的方程得,
所以直线的方程为.
故答案为:
例20.(2023·全国·高三专题练习)若动点A,B分别在直线l1:x+y-7=0和l2:x+y-5=0上移动,则AB的中点M到原点的距离的最小值为( )
A.3B.2C.3D.4
【答案】A
【解析】先求出点M所在直线的方程为l:x+y+m=0,再求出m的值和原点到直线l的距离即得解.依题意知AB的中点M的集合为与直线l1:x+y-7=0和l2:x+y-5=0距离都相等的直线,
则M到原点的距离的最小值为原点到该直线的距离.
设点M所在直线的方程为l:x+y+m=0,
根据平行线间的距离公式得
所以|m+7|=|m+5|,所以m=-6,
即l:x+y-6=0.
根据点到直线的距离公式得M到原点的距离的最小值为.
故选:A.
例21.(2023·全国·高三专题练习)直线关于直线对称的直线方程是( )
A.B.
C.D.
【答案】A
【解析】在直线上任取一点,设点关于直线的对称点为,
则,解得,即,
因为点在直线上,
所以,即,
所以所求直线方程为,
故选:A.
变式40.(2023·全国·高三专题练习)设直线与关于直线对称,则直线的方程是( )
A.B.
C.D.
【答案】A
【解析】联立,得,
取直线上一点,设点关于直线的对称点为,则,解得:,
直线的斜率,所以直线的方程为,
整理为:.
故选:A
变式41.(2023·全国·高三专题练习)直线关于直线对称的直线为( )
A.B.C.D.
【答案】C
【解析】设所求直线上的任意一点为
则关于直线对称点为
点在直线上
满足直线方程,即
直线关于直线对称的直线为
故选:C
变式42.(2023·全国·高三专题练习)如果直线与直线关于直线对称,那么( )
A.B.C.D.
【答案】A
【解析】在上取一点,
则由题意可得其关于直线的对称点在上,
所以,得,
在上取一点,
则其关于直线的对称点在上,
所以,得,
综上,
故选:A
变式43.(2023·全国·高三专题练习)求直线x+2y-1=0关于直线x+2y+1=0对称的直线方程( )
A.x+2y-3=0B.x+2y+3=0
C.x+2y-2=0D.x+2y+2=0
【答案】B
【解析】设对称直线方程为,
,解得或(舍去).
所以所求直线方程为.
故选:B
变式44.(2023·全国·高三专题练习)若两条平行直线:与:之间的距离是,则直线关于直线对称的直线方程为( )
A.B.
C.D.
【答案】A
【解析】因为直线:与:,
所以,
又两条平行直线:与:之间的距离是,
所以解得
即直线:,:,
设直线关于直线对称的直线方程为,
则,解得,
故所求直线方程为,
故选:A
变式45.(2023·全国·高三专题练习)两直线方程为,,则关于对称的直线方程为( )
A.B.
C.D.
【答案】C
【解析】设所求直线上任一点,关于直线的对称点,,
则,解出
点在直线上, 将式代入,得,
化简得,即为关于对称的直线方程.
故选:C
【解题方法总结】
求直线l关于直线对称的直线
若直线,则,且对称轴与直线l及之间的距离相等.
此时分别为,由,求得,从而得.
若直线l与不平行,则.在直线l上取异于Q的一点,然后求得关于直线对称的点,再由两点确定直线(其中).
题型八:直线系方程
例22.(2023·全国·高三专题练习)已知两直线和的交点为,则过两点的直线方程为 .
【答案】
【解析】依题意两直线和的交点为,
所以在直线上,
所以过两点所在直线方程为.
故答案为:
例23.(2023·全国·高三专题练习)经过直线3x-2y+1=0和直线x+3y+4=0的交点,且平行于直线x-y+4=0的直线方程为 .
【答案】x-y=0.
【解析】设直线方程为3x-2y+1+λ(x+3y+4)=0,再求出的值即得解.过两直线交点的直线方程可设为3x-2y+1+λ(x+3y+4)=0,
即(3+λ)x+(3λ-2)y+4λ+1=0,
因为它与直线x-y+4=0平行,
所以3+λ+3λ-2=0,
即λ=-,
故所求直线为x-y=0.
故答案为:x-y=0.
例24.(2023·全国·高三专题练习)已知坐标原点为O,过点作直线n不同时为零的垂线,垂足为M,则的取值范围是 .
【答案】
【解析】根据题意,直线,即,
则有,解可得,则直线恒过点.
设,又由与直线垂直,且为垂足,
则点的轨迹是以为直径的圆,其方程为,
所以;即的取值范围是;
故答案为.
变式46.(2023·高二课时练习)经过点和两直线;交点的直线方程为 .
【答案】
【解析】设所求直线方程为,
点在直线上,
,
解得,
所求直线方程为,即.
故答案为:.
变式47.(2023·全国·高二课堂例题)若直线l经过两直线和的交点,且斜率为,则直线l的方程为 .
【答案】
【解析】设直线l的方程为(其中为常数),即 ①.
又直线l的斜率为,则,解得.
将代入①式并整理,得,此即所求直线l的方程.
故答案为:.
变式48.(2023·全国·高一专题练习)设直线经过和的交点,且与两坐标轴围成等腰直角三角形,则直线的方程为 .
【答案】或
【解析】方法一:由,得,
所以两条直线的交点坐标为(14,10),
由题意可得直线的斜率为1或-1,
所以直线的方程为或,
即或.
方法二:设直线的方程为,整理得,
由题意,得,解得或,
所以直线的方程为或.
故答案为:或.
变式49.(2023·高二课时练习)经过直线3x+2y+6=0和2x+5y-7=0的交点,且在两坐标轴上的截距相等的直线方程为 .
【答案】x+y+1=0或3x+4y=0
【解析】由题意可设所求直线方程为,即
令,得
令,得
∵所求直线方程在两坐标轴上的截距相等
∴,即或
∴所求直线方程为或
故答案为或
【解题方法总结】
利用直线系方程求解.
【解题方法总结】
1.(2020•新课标Ⅲ)点到直线距离的最大值为
A.1B.C.D.2
【答案】
【解析】方法一:因为点到直线距离;
要求距离的最大值,故需;
,当且仅当时等号成立,
可得,当时等号成立.
方法二:由可知,直线过定点,
记,则点到直线距离.
故选:.
2.(2018•北京)在平面直角坐标系中,记为点到直线的距离.当、变化时,的最大值为
A.1B.2C.3D.4
【答案】
【解析】由题意,
当时,
.
的最大值为3.
故选:.
3.(2014•四川)设,过定点的动直线和过定点的直线交于点,则的取值范围是
A.,B.,C.,D.,
【答案】
【解析】由题意可知,动直线经过定点,
动直线即,经过点定点,
动直线和动直线的斜率之积为,始终垂直,
又是两条直线的交点,,.
设,则,,
由且,可得,
,
,,,,
,,
,,
故选:.
考点要求
考题统计
考情分析
(1)能根据斜率判定两条直线平行或垂直.
(2)能用解方程组的方法求两条直线的交点坐标.
(3)掌握平面上两点间的距离公式、点到直线的距离公式,会求两条平行直线间的距离.
2022年上海卷第7题,5分
2020年III卷第8题,5分
2020年上海卷第7题,5分
高考对两条直线的位置关系的考查比较稳定,考查内容、频率、题型难度均变化不大,备考时应熟练掌握两条直线的位置关系、距离公式、对称问题等,特别要重视两条直线的位置关系以及点到直线的距离公式这两个考点.
两直线方程
平行
垂直
(斜率存在)
(斜率不存在)
或
或中有一个为0,另一个不存在.
第02讲 排列、组合(十九大题型)(讲义)-2024年高考数学一轮复习讲义(新教材新高考): 这是一份第02讲 排列、组合(十九大题型)(讲义)-2024年高考数学一轮复习讲义(新教材新高考),文件包含第02讲排列组合十九大题型讲义原卷版docx、第02讲排列组合十九大题型讲义解析版docx等2份试卷配套教学资源,其中试卷共72页, 欢迎下载使用。
第01讲 统计(八大题型)(讲义)-2024年高考数学一轮复习讲义(新教材新高考): 这是一份第01讲 统计(八大题型)(讲义)-2024年高考数学一轮复习讲义(新教材新高考),文件包含第01讲统计八大题型讲义原卷版docx、第01讲统计八大题型讲义解析版docx等2份试卷配套教学资源,其中试卷共72页, 欢迎下载使用。
第05讲 椭圆及其性质(八大题型)(讲义)-2024年高考数学一轮复习讲义(新教材新高考): 这是一份第05讲 椭圆及其性质(八大题型)(讲义)-2024年高考数学一轮复习讲义(新教材新高考),文件包含第05讲椭圆及其性质八大题型讲义原卷版docx、第05讲椭圆及其性质八大题型讲义解析版docx等2份试卷配套教学资源,其中试卷共108页, 欢迎下载使用。












