云南省昆明市五华区2023-2024学年七年级上学期期末数学试题

这是一份云南省昆明市五华区2023-2024学年七年级上学期期末数学试题，共11页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

一、单选题
1．-4的绝对值是（ ）
A．-14B．14C．4D．-4
【答案】C
【解析】-4的绝对值是4，
故选：C．
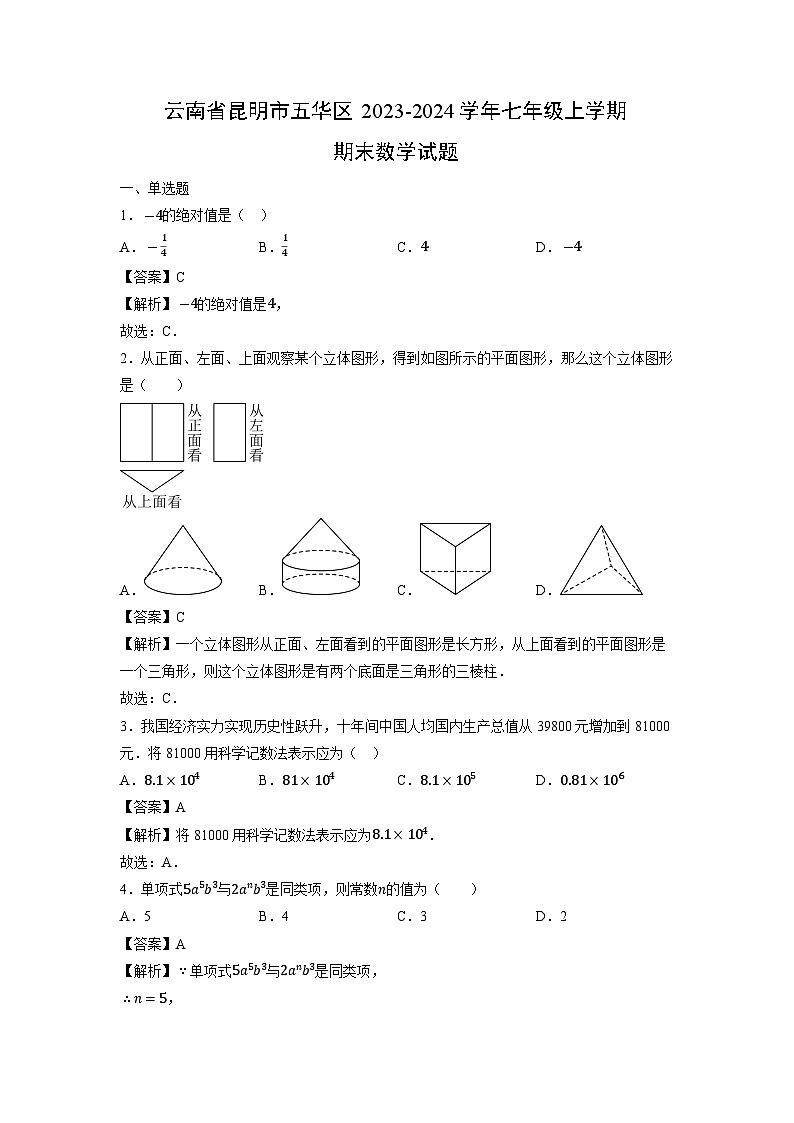
2．从正面、左面、上面观察某个立体图形，得到如图所示的平面图形，那么这个立体图形是（ ）
A．B．C．D．
【答案】C
【解析】一个立体图形从正面、左面看到的平面图形是长方形，从上面看到的平面图形是一个三角形，则这个立体图形是有两个底面是三角形的三棱柱．
故选：C．
3．我国经济实力实现历史性跃升，十年间中国人均国内生产总值从39800元增加到81000元．将81000用科学记数法表示应为（ ）
A．8.1×104B．81×104C．8.1×105D．0.81×106
【答案】A
【解析】将81000用科学记数法表示应为8.1×104．
故选：A．
4．单项式5a5b3与2anb3是同类项，则常数n的值为（ ）
A．5B．4C．3D．2
【答案】A
【解析】∵单项式5a5b3与2anb3是同类项，
∴n=5，
故选：A．
5．有理数a，b在数轴上的对应点的位置如图所示，下列结论中正确的是（ ）
A．a+b>0B．ab>0C．a>bD．a-b>0
【答案】C
【解析】A、∵a<-2<0∴a>b，a+b<0，故此选项错误；
B、∵a<-2<0∴ab<0，故此选项错误；
C、∵a<-2<0∴a>b，故此选项正确；
D、∵a<-2<0∴a-b<0，故此选项错误．
故选：C．
6．如果关于x的方程2x+m=4的解是x=-1，那么m的值是（ ）
A．-6B．2C．4D．6
【答案】D
【解析】把x=-1代入2x+m=4，得-2+m=4，
解得m=6．
故选：D．
7．如图，某海域有三个小岛A，B，O，在小岛O处观测到小岛A在它的北偏东70°的方向上，观测到小岛B在它的南偏西15°的方向上，则∠AOB的度数是（ ）
A．85°B．105°C．115°D．125°
【答案】D
【解析】如图，由题意得：∠1=70°,∠2=15°，
∴∠3=90°-∠1=20°，
∴∠AOB=∠2+∠3+90°=15°+20°+90°=125°,
故选：D．
8．已知2a=b+1，则下列等式中不成立的是（ ）
A．2a-1=bB．2a+3=b+3
C．a=b2+12D．4a=2b+2
【答案】B
【解析】A．2a=b+1，则2a-1=b，所以A选项不符合题意；
B．2a=b+1，则2a+3=b+4，所以B选项符合题意；
C．2a=b+1，则a=b2+12，所以C选项不符合题意；
D．2a=b+1，则4a=2b+2，所以D选项不符合题意；
故选：B．
9．下列说法中，正确的是（ ）
A．射线AB和射线BA是同一条射线
B．如果AC=BC，那么C是线段AB的中点
C．如果两个角互补，那么它们的角平分线所在直线的夹角为90°
D．如果两个角是同一个角的补角，那么它们相等
【答案】D
【解析】A. 射线AB和射线BA的端点不同，不是同一条射线，
该说法错误，不符合题意；
B. 如果AC,BC在同一直线上，AC=BC，则C是线段AB的中点，
因为无法确定AC,BC是否在同一直线，故该说法错误，不符合题意；
C. 如果相邻的两个角互补，那么它们的角平分线所在直线的夹角为90°，
故该说法错误，不符合题意；
D. 如果两个角是同一个角的补角，那么它们相等，
该说法正确，符合题意．
故选：D．
10．《九章算术》是人类科学史上应用数学的“算经之首”，书中记载：今有共买物，人出八，盈三；人出七，不足四．问人数、物价各几何？意思是：现有几个人共买一件物品，每人出8钱，多出3钱；每人出7钱，还差4钱．问：人数、物价各是多少？若设物价是x钱，根据题意列一元一次方程，正确的是（ ）
A．x-38=x+47B．x+38=x-47C．x-48=x+37D．x+48=x-37
【答案】B
【解析】设物价是x钱，则根据可得：x+38=x-47
故选B．
11．佳佳同学解一元一次方程14+2x-12=12-1-2x4的过程如下：
解：去分母，得1+2(2x-1)=2-(1-2x)，第一步
去括号，得1+4x-2=2-1-2x，第二步
移项，得4x+2x=2-1-1+2，第三步
合并同类项，得6x=2，第四步
系数化为1，得x=13．
前四个步骤中，开始出现错误的是（ ）
A．第一步B．第二步C．第三步D．第四步
【答案】B
【解析】14+2x-12=12-1-2x4,
去分母，得1+2(2x-1)=2-(1-2x)，第一步
去括号，得1+4x-2=2-1+2x，第二步
∴出现错误在第二步，去括号时，括号前面的负号，去括号后，括号内第二项没有改变符号；
故选：B.
12．在-26.8，5，-19，-0.34，227，-2中，负分数有（ ）
A．5个B．4个C．3个D．2个
【答案】C
【解析】-26.8，-19，-0.34是负分数；
5是正整数，227是正分数，-2是负整数．
故选C．
13．将12.28°转化为度、分、秒的形式为（ ）
A．12°20'8″B．12°16'48″C．12°12'48″D．12°28″
【答案】B
【解析】12.28°=12°+0.28×60'
=12°+16'+0.8×60″
=12°16'48″；
故选：B．
14．若x-3y=-4，则x-3y2+2x-6y-10的值为（ ）
A．14B．2C．-18D．-2
【答案】D
【解析】∵ x-3y=-4，
∴x-3y2+2x-6y-10，
=x-3y2+2x-3y-10
=x-3y2+2x-3y-10
=16-8-10
=-2，
故选：D．
15．一个由若干奇数排成的数阵，用如图所示的框去框住四个数，并求出它们的和．移动这个框，框住四个数的和可能是（ ）
A．114B．122C．220D．84
【答案】B
【解析】设最小的一个数为x，则另外三个数为x+8，x+10，x+12，显然x的个位数字只可能是3、5、7，框住的四个数之和为x+x+8+x+10+x+12=4x+30．
当4x+30=114时，x=21，21为最左边的数，不合题意；
当4x+30=122时，x=23，符合题意；
当4x+30=220时，x=47.5，不合题意；
当4x+30=84时，x=13.5，不合题意．
故选B．
二、填空题
16．用四舍五入法把3.1415926精确到0.01，所得到的近似数为 ．
【答案】3.14
【解析】3.1415926≈3.14.
17．如图，C，D是线段AB的三等分点，E是线段BD的中点，若CE=3，则AB= ．
【答案】6
【解析】∵C，D是线段AB的三等分点，
∴AC=CD=DB，
∵E是线段BD的中点，
∴DE=BE=12BD，
∵CE=CD+DE=3，
∴AB=AC+CD+DE+BE=2(CD+DE)=2CE=2×3=6．
18．如图（图中长度单位：m)，阴影部分的面积是 m2.
【解析】由题意得：
S阴影部分=2+3xx+3-2x
=2x+6+3x2+9x-2x
=(3x2+9x+6)(m2)．
19．电影《哈利•波特》中，小哈利波特穿越墙进入“934站台”的镜头（如示意图的Q站台），构思奇妙，能给观众留下深刻的印象．若A、B站台分别位于-23，83处，AP=2PB，则P站台用类似电影的方法可称为“ 站台”．
【答案】159或6
【解析】AB=83--23=103，
AP=103×22+1=209，或AP=103×2=203，
P：-23+209=149=159，或-23+203=183=6．
故P站台用类似电影的方法可称为“159站台”或者“6站台”．
三、解答题
20．（1）计算：-12+(-6)-(-28)；
（2）计算：-22×52-34-4÷-232；
（3）解方程：3x-12+1=4x+25．
解：（1）原式=-12-6+28=10．
（2）-22×52-34-4÷-232；
=-4×74-4÷49
=-4×74-4×94
=-7-9
=-16．
（3）3x+12+1=4x+25,
去分母，得53x+1+10=24x+2，
去括号，得15x+5+10=8x+4，
移项、合并同类项，得7x=-11，
系数化为1，得x=-117．
21．先化简，再求值：26y2-3y+2+2y-1-2+12y2，其中y=12．
解：26y2-3y+2+2y-1-2+12y2
=12y2-6y+4+2y-2-2-12y2
=-4y；
当y=12时，原式=-4×12=-2．
22．根据题意，补全解题过程：
如图，已知射线OB，OM，ON在∠AOD内部，OM平分∠AOB，ON平分∠BOD，若∠AOD=156°，∠DON=48°，求∠AOM的度数．
解：∵ON平分∠BOD，
∴______=2∠DON，
∵∠DON=48°，
∴∠BOD=______，
∵∠AOB=______-∠BOD，∠AOD=156°，
∴∠AOB=______，
∵OM平分∠AOB，
∴∠AOM=12______＝______．
解：∵ON平分∠BOD，
∴∠BOD=2∠DON，
∵∠DON=48°，
∴∠BOD=96°，
∵∠AOB=∠AOD-∠BOD，∠AOD=156°，
∴∠AOB=60°，
∵OM平分∠AOB，
∴∠AOM=12∠AOB=30°．
故答案为：∠BOD，96°，∠AOD，60°，∠AOB，30°．
23．饺子是中国传统食物，用一张小圆形面皮包馅制作而成，形如半月或元宝；馅饼也是非常流行的一种美食，用一张大圆形面皮包馅制作而成，呈扁圆形．元旦当天，小盛和爸爸、妈妈一起制作美味的饺子和馅饼，小盛向爸爸学习制作圆形面皮，一共制作了大、小两种圆形面皮共100张，爸爸和妈妈一起包饺子和馅饼，正好用完所有制作的大小面皮，小盛发现饺子的数量比馅饼数量的4倍多5个．请你根据以上信息，求出所包饺子和馅饼各多少个？（列方程解答）
解：设包了x个馅饼，则包了(4x+5)个饺子．根据题意得：
x+4x+5=100，
解得x=19，
所以，4x+5=4×19+5=81．
答：包了81个饺子，19个馅饼．
24．如图，已知三点A，B，C，作直线AB．
(1)用语句表述图中点C与直线AB的关系：______；
(2)用直尺和圆规完成以下作图（保留作图痕迹）：连接CA，在线段CA的延长线上作线段AD，使AD=AB．
(3)连接BC，比较线段DC与线段BC的长短，并将下面的推理补充完整：
∵ DC=AD+AC，AD=AB，
∴ DC=AB+AC，
∵ AB+AC______BC，（______）（填推理的依据）
∴ DC______BC．
解：（1）点C与直线AB的关系为：点C在直线AB外，
故答案为：点C在直线AB外；
（2）作出图如图所示；
（3）∵ DC=AD+AC，AD=AB，
∴ DC=AB+AC，
∵ AB+AC>BC，（两点之间，线段最短）
∴ DC>BC，
故答案为：>；两点之间，线段最短；>．
25．某商户每日要购进500千克小龙虾，下表是该商户记录的本周小龙虾进价的浮动情况：
注：正号表示价格比前一天上涨，负号表示价格比前一天下降．
已知小龙虾上周日的进价为每千克23元，这周四的进价为每千克24元．
(1)求m的值和本周内购进小龙虾的最高单价；
(2)商户周五将当天购进的小龙虾以每千克25元全部售出，且出售时小龙虾有4％的损耗，求该商户在本周星期五当天的收益．
解：（1）星期一的小龙虾每千克进价为：23-1=22（元）；
星期二的小龙虾每千克进价为：22+2.5=24.5（元）；
星期三的小龙虾每千克进价为：24.5-2=22.5（元）；
星期四的小龙虾每千克进价为：24元；
星期五的小龙虾每千克进价为：24-3=21（元）；
星期六的小龙虾每千克进价为：21+2=23（元）；
星期日的小龙虾每千克进价为：23+2=25（元）．
m=24-22.5=+1.5（元）．
综上可得：21<22<22.5<23<24<24.5<25，
所以，本周内购进小龙虾的最高单价是每千克25元．
答：m的值为+1.5；本周内购进小龙虾的最高单价是每千克25元．
（2）由（1）可知：星期五的小龙虾每千克进价为21元，
500×1-4%×25-500×21=12000-10500=1500（元），
答：该商户在本周星期五当天的收益情况是赚钱1500元．
26．用A、B两种型号的机器生产相同的产品，产品装入同样规格的包装箱后运往仓库．已知每台B型机器比A型机器一天多生产2件产品，3台A型机器一天生产的产品恰好能装满5箱，4台B型机器一天生产的产品恰好能装满7箱．每台A型机器一天生产多少件产品？每箱装多少件产品？
下面是解决该问题的两种思路，请选择其中一种思路，进行解答．（不需要填空）
思路一：若设每台A型机器一天生产x件产品，则每台B型机器一天生产(x+2)件产品，3台A型机器一天共生产______件产品，4台B型机器一天共生产______件产品，再根据相等关系：______，就可以列出方程解决问题．
思路二：若设每箱装x件产品，则3台A 型机器一天共生产_____件产品，4台B型机器一天共生产________件产品，再根据相等关系：________，就可以列出方程解决问题．
解：思路一解法：
设每台A型机器一天生产x件产品，根据题意得：
3x5=4x+27，
解得x=40．
所以3x5=3×405=24（件）．
答：每台A型机器一天生产40件产品，每箱装24件产品．
思路二解法：
设每箱装x件产品，根据题意得：5x3=7x4-2，
解得x=24．
所以5x3=5×243=40（件）．
答：每台A型机器一天生产40件产品，每箱装24件产品．
27．如图1，点A，B，C是同一直线上互不重合的三个点，在线段AB，BC，CA中，若有一条线段的长度恰好是另一条线段长度的一半，则称A，B，C三点存在“半分关系”．
(1)当点C是线段AB的中点时，A，B，C三点_______“半分关系”（填“存在”或“不存在”）；
(2)已知AB=9 cm，点C在线段AB上，若A，B，C三点存在“半分关系”，求线段AC的长度；
(3)如图2，已知点D，O，E是数轴上互不重合的三个点，点O为原点，点D表示的数是t（t是负数），且D，O，E三点存在“半分关系”，直接写出点E表示的数的最大值与最小值的差（用含t的式子表示）．
解：（1）存在；
∵当点C是线段AB的中点时，
∴AC=BC=12AB．
∴A，B，C三点存在“半分关系”．
（2）①当AC=12AB时，A，B，C三点存在“半分关系”，
∵AB=9 cm，
∴AC=12AB=92 cm．
②当BC=12AC时，A，B，C三点存在“半分关系”，
此时AC=23AB．
∵AB=9 cm，
∴AC=6 cm．
③当AC=12BC时，A，B，C三点存在“半分关系”，
此时AC=13AB．
∵AB=9 cm，
∴AC=3 cm．
综上，AC的长为92 cm或6 cm或3 cm；
（3）点E表示的数的最大值与最小值的差为-5t．
理由如下：
当点E在点O的右侧，且OE=2OD时取最大值．
∵点D表示的数是t，
∴OE=-2t，
即点E表示的数为-2t，
当点E在点D的左侧，且DE=2OD时取最小值，
∵点D表示的数是t，
∴DE=OD+DE=-t-2t=-3t，
即点E表示的数为3t，
∴点E表示的数的最大值与最小值的差为-2t-3t=-5t．
星期
一
二
三
四
五
六
日
价格/（元/千克）
-1
+2.5
-2
m
-3
+2
+2