人教B版 (2019)必修 第四册11.1.3 多面体与棱柱授课课件ppt

这是一份人教B版 (2019)必修 第四册11.1.3 多面体与棱柱授课课件ppt，共33页。PPT课件主要包含了新知初探·自主学习，课堂探究·素养提升，平面多边形，都在这个平面的同一侧，互相平行，公共边，公共顶点，答案D，答案C，答案ABC等内容，欢迎下载使用。

课程标准1.认识棱柱及简单组合体的结构特征，能运用这些特征描述现实生活中简单物体的结构．2．知道棱柱的表面积的计算公式，能用公式解决简单的实际问题．
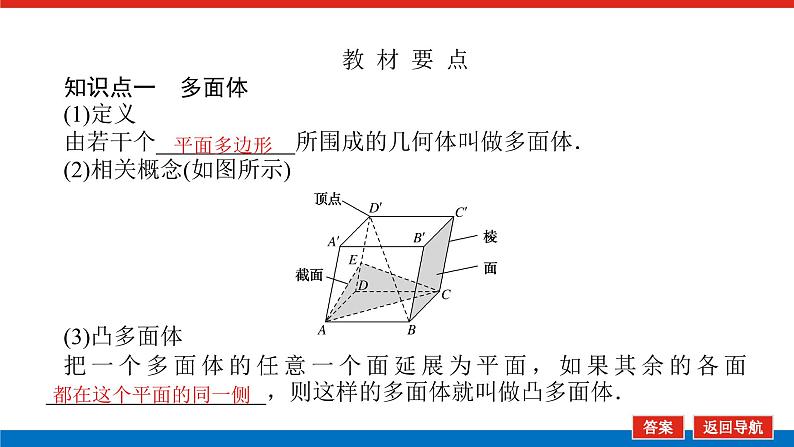
教 材 要 点知识点一　多面体(1)定义由若干个____________所围成的几何体叫做多面体．(2)相关概念(如图所示)(3)凸多面体把一个多面体的任意一个面延展为平面，如果其余的各面___________________，则这样的多面体就叫做凸多面体．
状元随笔　长方体、正方体是多面体吗？[提示]　是．长方体是由6个矩形围成的，正方体是由6个正方形围成的，均满足多面体的定义．最简单的多面体由几个面所围成？[提示]　四个．
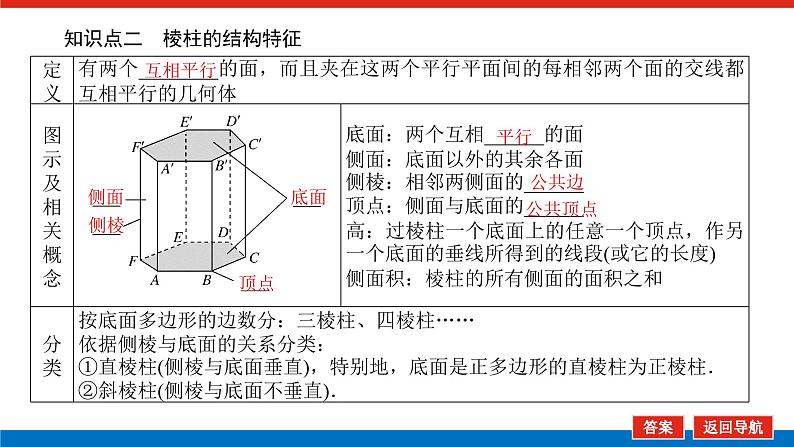
知识点二　棱柱的结构特征
状元随笔　(1)棱柱的底面是固定不变的吗？[提示]　不一定．例如：正方体、长方体都是棱柱，它们的任何一对对面都可以作为其底面．(2)平行六面体是棱柱吗？写出{四棱柱}、{平行六面体}、{直平行六面体}之间的包含关系？[提示]　依据棱柱的定义可知，平行六面体是棱柱．{四棱柱}、{平行六面体}、{直平行六面体}之间的包含关系为：{四棱柱}⊇{平行六面体}⊇{直平行六面体}．
基 础 自 测1．下列几何体中是棱柱的个数有(　　)A．5个 B．4个C．3个 D．2个
解析：由棱柱的定义知①③是棱柱，选D.
2．四棱柱有几条侧棱，几个顶点(　　)A．四条侧棱、四个顶点B．八条侧棱、四个顶点C．四条侧棱、八个顶点D．六条侧棱、八个顶点
解析：由四棱柱的结构特征知它有四条侧棱，八个顶点．
3．(多选)下列叙述中正确的是(　　)A．棱柱的面中，至少有两个面相互平行B．棱柱的各个侧面都是平行四边形C．棱柱的两底面是全等的多边形D．棱柱中两个互相平行的平面一定是棱柱的底面
解析：定义1：上下底面平行且全等，侧棱平行且相等的封闭几何体叫棱柱．定义2：有两个面互相平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行，这些面围成的几何体叫棱柱；正四棱柱，正六棱柱中，相对的侧面都是互相平行的平面，故D错误．故选ABC.
4．一个棱柱至少有________个面；面数最少的棱柱有________个顶点，有________条棱．
解析：面数最少的棱柱是三棱柱，有5个面，6个顶点，9条棱．
题型1　棱柱的概念例1　(1)下列描述中，不是棱柱的结构特征的是(　　)A．有一对面互相平行B．侧面都是四边形C．相邻两个侧面的公共边都互相平行D．所有侧棱都交于一点
【解析】　由棱柱的结构特征知D错．
(2)下列关于棱柱的叙述，错误的是(　　)A．所有的棱柱两个底面都平行B．所有的棱柱一定有两个面互相平行，其余各面每相邻面的公共边互相平行C．有两个面互相平行，其余各面都是平行四边形的几何体一定是棱柱D．棱柱至少有五个面
【解析】　对于A，B，D，显然是正确的；对于C，与棱柱的定义比，没有说明各顶点都在平行的这两个面上这一条件，因此所围成的几何体不一定是棱柱．如图所示的几何体就不是棱柱．所以C错误．
状元随笔　判断一个几何体是何种几何体，一定要紧扣几何体的结构特征，注意概念中的特殊字眼，切不可马虎大意，如棱柱的概念中的“相邻”，棱锥的概念中的“公共顶点”，棱台的概念中的“棱锥”“平行”等．
方法归纳棱柱结构特征的辨析技巧(1)扣定义：判定一个几何体是否为棱柱的关键是棱柱的定义．①看“面”，即观察这个多面体是否有两个互相平行的面，其余各面都是平行四边形；②看“线”，即观察每相邻两个四边形的公共边是否平行．(2)举反例：通过举反例，如与常见几何体或实物模型、图片等不吻合，给予排除．
跟踪训练1　下列关于棱柱的说法正确的个数是(　　)①四棱柱是平行六面体；②有两个面平行，其余各面都是平行四边形的几何体是棱柱；③有两个面平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行的几何体是棱柱；④底面是正多边形的棱柱是正棱柱．A．1 B．2C．3 D．4
解析：四棱柱的底面可以是任意四边形；而平行六面体的底面必须是平行四边形，故①不正确；说法③就是棱柱的定义，故③正确；对比定义，显然②不正确；底面是正多边形的直棱柱是正棱柱，故④不正确．
题型2　几种常见四棱柱的关系例2　下列说法中正确的是(　　)A．直四棱柱是直平行六面体B．直平行六面体是长方体C．六个面都是矩形的四棱柱是长方体D．底面是正方形的四棱柱是直四棱柱
【解析】　直四棱柱的底面不一定是平行四边形，故A错；直平行六面体的底面不一定是矩形，故B错；C正确；底面是正方形的四棱柱不一定是直四棱柱，故D错．
方法归纳几种常见四棱柱的关系
跟踪训练2　一个棱柱是正四棱柱的条件是(　　)A．底面是正方形，有两个面是矩形的四棱柱B．底面是正方形，两个侧面垂直于底面的四棱柱C．底面是菱形，且有个顶点处的两条棱互相垂直的四棱柱D．底面是正方形，每个侧面都是全等的矩形的四棱柱
解析：选项A、B中，两个面为相对侧面时，四棱柱不一定是直四棱柱，C中底面不是正方形，故排除选项A、B、C，所以选D.
题型3　多面体的表面展开图例3　(1)一个正四棱柱的体对角线的长是9 cm，全面积等于144 cm2，则这个棱柱的侧面积为________cm2；
(2)在长方体ABCD-A1B1C1D1中，AB＝2 cm，BC＝3 cm，CC1＝4 cm，一只蚂蚁从A点沿着表面爬行到C1点参加某项活动，长方体6个面都可爬行，蚂蚁前进的最短距离是多少？
分三种情况计算，比较大小得最短距离．
方法归纳多面体展开图问题的解题策略(1)由展开图复原几何体：首先想象出复原后的几何体，再将展开图中的面、点标注到该几何体上．(2)多面体表面上两点间的最短距离问题常常要归纳为求平面上两点间的最短距离问题．常见的解法是先把多面体的表面展开成平面图形，再用平面几何知识求有关线段的长度．
跟踪训练3　(1)已知某长方体同一顶点上的三条棱长分别为1，2，3，则该长方体的表面积为(　　)A．22 B．20C．10 D．11
解析：所求长方体的表面积S＝2×(1×2)＋2×(1×3)＋2×(2×3)＝22.
教材反思1．本节课的重点是理解并掌握棱柱的定义和结构特征，难点是在描述和判断几何体结构特征的过程中培养观察能力和空间想象能力．2．本节课要重点掌握的规律方法(1)有关棱柱结构特征的解题策略．(2)绘制展开图和由展开图还原几何体的方法．3．本节课的易错点是理解棱柱的结构特征及其关系中出现偏差而致错．