

浙江省杭州市城区六校联考2024年九上数学开学调研模拟试题【含答案】
展开一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求)
1、(4分)如图,□ABCD中,EF过对角线的交点O,AB=4,AD=3,OF=1.3,则四边形BCEF的周长为( )
A.8.3B.9.6C.12.6D.13.6
2、(4分)某校学生志愿服务小组在“学雷锋”活动中购买了一批牛奶到敬老院慰问老人.如果分给每位老人4盒牛奶,那么剩下28盒牛奶;如果分给每位老人5盒牛奶,那么最后一位老人分得的牛奶不足4盒,但至少1盒.则这个敬老院的老人最少有( )
A.29人B.30人C.31人D.32人
3、(4分)若无解,则m的值是( )
A.3B.﹣3C.﹣2D.2
4、(4分)关于的一元二次方程有两个不相等的实数根,则实数的取值范围是( )
A.B.C.D.
5、(4分)一次函数 y 2x 2 的大致图象是( )
A.B.C.D.
6、(4分)将三角形纸片△ABC按如图所示的方式折叠,使点B落在边AC上,记为点B′,折痕为EF.已知AB=AC=8,BC=10,若以点B′,F,C为顶点的三角形与△ABC相似,那么BF的长度是( ).
A.5B.C.或4D.5或
7、(4分)如图,正方形OABC的兩辺OA、OC分別在x轴、y轴上,点D(5,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是( )
A.(1,10)B.(-2,0)C.(2,10)或(-2,0)D.(10,2)或(-2,0)
8、(4分)一个关于x的一元一次不等式组的解集在数轴上的表示如图,则该不等式组的解集是( )
A.x>1B.x≥1C.x>3D.x≥3
二、填空题(本大题共5个小题,每小题4分,共20分)
9、(4分)长方形的长是宽的2倍,对角线长是5cm,则这个长方形的长是______.
10、(4分)某天工作人员在一个观测站测得:空气中PM2.5含量为每立方米0.0000023g,则将0.0000023用科学记数法表示为_____.
11、(4分)函数y=x+1与y=ax+b的图象如图所示,那么,使y、y的值都大于0的x的取值范围是______.
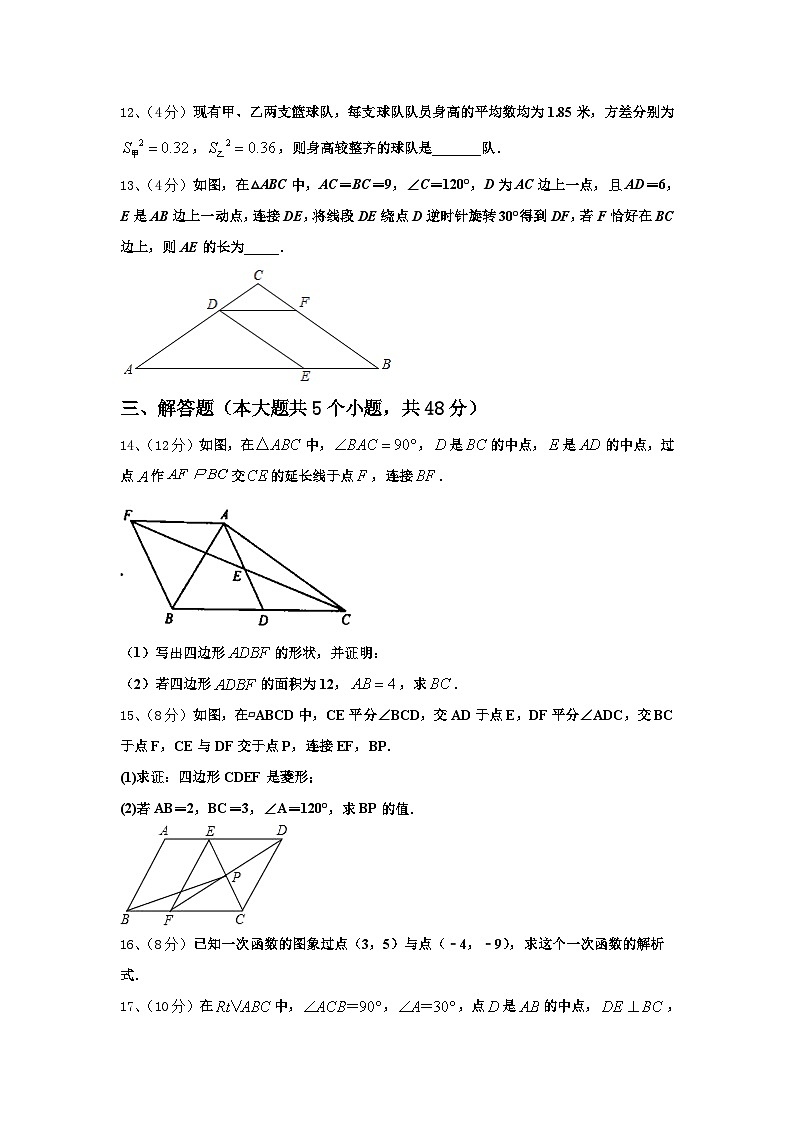
12、(4分)现有甲、乙两支篮球队,每支球队队员身高的平均数均为1.85米,方差分别为,,则身高较整齐的球队是_______队.
13、(4分)如图,在△ABC中,AC=BC=9,∠C=120°,D为AC边上一点,且AD=6,E是AB边上一动点,连接DE,将线段DE绕点D逆时针旋转30°得到DF,若F恰好在BC边上,则AE的长为_____.
三、解答题(本大题共5个小题,共48分)
14、(12分)如图,在中,,是的中点,是的中点,过点作交的延长线于点,连接.
(1)写出四边形的形状,并证明:
(2)若四边形的面积为12,,求.
15、(8分)如图,在▱ABCD中,CE平分∠BCD,交AD于点E,DF平分∠ADC,交BC于点F,CE与DF交于点P,连接EF,BP.
(1)求证:四边形CDEF是菱形;
(2)若AB=2,BC=3,∠A=120°,求BP的值.
16、(8分)已知一次函数的图象过点(3,5)与点(﹣4,﹣9),求这个一次函数的解析式.
17、(10分)在中,,,点是的中点,,垂足为,连接.
(1)如图1,与的数量关系是__________.
(2)如图2,若是线段上一动点(点不与点、重合),连接,将线段绕点逆时针旋转得到线段,连接,请猜想三者之间的数量关系,并证明你的结论;
18、(10分)如图,将一矩形纸片OABC放在平面直角坐标系中,O(1,1),A(6,1),C(1,3),动点F从点O出发以每秒1个单位长度的速度沿OC向终点C运动,运动秒时,动点E从点A出发以相同的速度沿AO向终点O运动,当点E、F其中一点到达终点时,另一点也停止运动设点E的运动时间为t:(秒)
(1)OE= ,OF= (用含t的代数式表示)
(2)当t=1时,将△OEF沿EF翻折,点O恰好落在CB边上的点D处
①求点D的坐标及直线DE的解析式;
②点M是射线DB上的任意一点,过点M作直线DE的平行线,与x轴交于N点,设直线MN的解析式为y=kx+b,当点M与点B不重合时,S为△MBN的面积,当点M与点B重合时,S=1.求S与b之间的函数关系式,并求出自变量b的取值范围.
B卷(50分)
一、填空题(本大题共5个小题,每小题4分,共20分)
19、(4分)当时,分式的值是________.
20、(4分)如图,若在象棋盘上建立平面直角坐标系xOy,使“帥”的坐标为(﹣1,﹣2),“馬”的坐标为(2,﹣2),则“兵”的坐标为__.
21、(4分)化简分式:=_____.
22、(4分)如图所示,某人在D处测得山顶C的仰角为30°,向前走200米来到山脚A处,测得山坡AC的坡度i=1∶0.5,则山的高度为____________米.
23、(4分)如果从初三(1)、(2)、(3)班中随机抽取一个班与初三(4)班进行一场拔河比赛,那么恰好抽到初三(1)班的概率是_____.
二、解答题(本大题共3个小题,共30分)
24、(8分)某超市在端午节期间开展优惠活动,凡购物者可以通过转动转盘的方式享受折扣优惠,本次活动共有两种方式,方式一:转动转盘甲,指针指向A区域时,所购买物品享受9折优惠、指针指向其它区域无优惠;方式二:同时转动转盘甲和转盘乙,若两个转盘的指针指向每个区域的字母相同,所购买物品享受8折优惠,其它情况无优惠.在每个转盘中,指针指向每个区城的可能性相同(若指针指向分界线,则重新转动转盘)
(1)若顾客选择方式一,则享受9折优惠的概率为多少;
(2)若顾客选择方式二,请用树状图或列表法列出所有可能,并求顾客享受8折优惠的概率.
25、(10分)已知某开发区有一块四边形的空地ABCD,如图所示,现计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,问要多少投入?
26、(12分)如图,折叠长方形的一边AD,使点D落在BC边上的点F处,BC=15,AB=9.
求:(1)FC的长;(2)EF的长.
参考答案与详细解析
一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求)
1、B
【解析】
解:根据平行四边形的中心对称性得:OF=OE=1.1.∵▱ABCD的周长=(4+1)×2=14
∴四边形BCEF的周长=×▱ABCD的周长+2.2=9.2.故选B.
2、B
【解析】
设这个敬老院的老人有x人,则有牛奶(4x+28)盒,根据关键语句“如果分给每位老人5盒牛奶,那么最后一位老人分得的牛奶不足4盒,但至少1盒”可得不等式组:
, 解得:29<x≤1.
∵x为整数,∴x最少为2.故选B.
3、D
【解析】
方程两边同乘以x-3可得m+1-x=0,因无解,可得x=3,代入得m=2,故选D.
4、B
【解析】
由方程有两个不相等的实数根结合根的判别式,可得出△=36-1k>0,解之即可得出实数k的取值范围.
【详解】
∵方程x2-1x+k=0有两个不相等的实数根,
∴△=(-1)2-1k=16-1k>0,
解得:k<1.
故选:B.
此题考查根的判别式,牢记“当△>0时,方程有两个不相等的实数根”是解题的关键.
5、A
【解析】
先判断出k、b的值,再根据一次函数的性质可画出函数的大致图象.
【详解】
解:∵k=2,b=-2,
∴函数y=2x-2的图象经过第一、三、四象限.
故选:A.
一次函数y=kx+b的图象有四种情况:
①当k>0,b>0,函数y=kx+b的图象经过第一、二、三象限;
②当k>0,b<0,函数y=kx+b的图象经过第一、三、四象限;
③当k<0,b>0时,函数y=kx+b的图象经过第一、二、四象限;
④当k<0,b<0时,函数y=kx+b的图象经过第二、三、四象限.
6、D
【解析】
根据折叠得到BF=B′F,根据相似三角形的性质得到或,设BF=x,则CF=10-x,即可求出x的长,得到BF的长,即可选出答案.
【详解】
解:∵△ABC沿EF折叠B和B′重合,
∴BF=B′F,
设BF=x,则CF=10-x,
∵当△B′FC∽△ABC,
,
∵AB=8,BC=10,
∴,解得:x=,
即:BF=,
当△FB′C∽△ABC,,
,
解得:x=5,
故BF=5或,
故选:D.
本题主要考查了相似三角形的性质,以及图形的折叠问题,解此题的关键是设BF=x,根据相似三角形的性质列出比例式.
7、C
【解析】
根据题意,分顺时针旋转和逆时针旋转两种情况,求出点D′到x轴、y轴的距离,即可判断出旋转后点D的对应点D′的坐标是多少即可.
【详解】
解:因为点D(5,3)在边AB上,
所以AB=BC=5,BD=5-3=2;
(1)若把△CDB顺时针旋转90°,
则点D′在x轴上,OD′=2,
所以D′(-2,0);
(2)若把△CDB逆时针旋转90°,
则点D′到x轴的距离为10,到y轴的距离为2,
所以D′(2,10),
综上,旋转后点D的对应点D′的坐标为(-2,0)或(2,10).
故选C.
本题考查坐标与图形变化-旋转,考查了分类讨论思想的应用,解答此题的关键是要注意分顺时针旋转和逆时针旋转两种情况.
8、C
【解析】
试题解析:一个关于x的一元一次不等式组的解集在数轴上的表示如图,
则该不等式组的解集是x>1.
故选C.
考点:在数轴上表示不等式的解集.
二、填空题(本大题共5个小题,每小题4分,共20分)
9、
【解析】
设矩形的宽是a,则长是2a,再根据勾股定理求出a的值即可.
【详解】
解:设矩形的宽是a,则长是2a,
对角线的长是5cm,
,
解得,
这个矩形的长,
故答案是:.
考查的是矩形的性质,勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.
10、2.3×10﹣1.
【解析】
绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
【详解】
0.0000023左起第一个不为零的数字前面有1个0,
所以0.000 0023=2.3×10﹣1,
故答案为2.3×10﹣1.
本题考查用科学记数法表示较小的数,一般形式为a×10﹣n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.
11、−1
根据x轴上方的图象的y值大于0进行解答.
【详解】
如图所示,x>−1时,y>0,
当x<2时,y>0,
∴使y、y的值都大于0的x的取值范围是:−1
12、甲
【解析】
根据方差的意义解答.方差,通俗点讲,就是和中心偏离的程度,用来衡量一批数据的波动大小(即这批数据偏离平均数的大小). 在样本容量相同的情况下,方差越大,说明数据的波动越大,越不稳定.
【详解】
∵<,
∴身高较整齐的球队是甲队。
故答案为:甲.
此题考查极差、方差与标准差,解题关键在于掌握其性质.
13、3+
【解析】
由,可知,又有,联想一线三等角模型,延长到,使,得,进而可得,,由于,即可得是直角三角形,易求,由即可解题.
【详解】
解:如图,延长到,使,连接,
,,
,,
,
又,
,
在和中,
,
,,
,
,
设,则,由得:
,
解得,(不合题意舍去),
,
,
故答案为:.
本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了全等三角形的判定与性质和等腰直角三角形的性质.本题解题关键是通过一线三等角模型构造全等三角形,从而得到.
三、解答题(本大题共5个小题,共48分)
14、(1)详见解析;(2)
【解析】
(1)由“AAS”可证△AEF≌△DEC,可得AF=CD,由直角三角形的性质可得AD=BD=CD,由菱形的判定是可证ADBF是菱形.
(2)由题意可得S△ABC=S四边形ADBF=12,可得AC的长,由勾股定理可求BC的长.
【详解】
解:解:(1)四边形ADBF是菱形,
理由如下:∵E是AD的中点,
∴AE=DE,
∵AF∥BC
∴∠AFE=∠DCE,且∠AEF=∠CED,AE=DE
∴△AEF≌△DEC(AAS)
∴AF=CD,
∵点D是BC的中点
∴BD=DC
∴AF=BD,且AF∥CD
∴四边形ADBF是平行四边形,
∵∠BAC=90°,D是BC的中点,
∴AD=BD,
∴平行四边形ADBF是菱形
(2)∵四边形ADBF的面积为12,
∴S△ABD=6
∵D是BC的中点
∴S△ABC=12=×AB×AC
∴12=×4×AC
∴AC=6,
∴BC=.
本题考查菱形的性质及判定,利用全等三角形的性质证得AF=CD是解题的关键,注意菱形面积公式的应用.
15、 (1)证明见解析;(2)BP的值为.
【解析】
(1)利用平行四边形的性质和角平分线的定义可求,可证得结论CD=CF=DE;
(2)过P作于PG⊥BC于G,在Rt△BPG中可求得PG和CG的长,则可求得BG的长,在Rt△BPG中,由勾股定理可求得BP的长.
【详解】
(1)证明:∵四边形ABCD为平行四边形,
∴AD∥BC,
∴∠EDF=∠DFC,
∵DF平分∠ADC,
∴∠EDF=∠CDF,
∴∠DFC=∠CDF,
∴CD=CF,
同理可得CD=DE,
∴CF=DE,且CF∥DE,
∴四边形CDEF为菱形;
(2)解:如图,过P作PG⊥BC于G,
∵AB=2,BC=3,∠A=120°,且四边形CDEF为菱形,
∴CF=EF=CD=AB=2,∠ECF=∠BCD=∠A=60°,
∴△CEF为等边三角形,
∴CE=CF=2,
∴PC=CE=1,
∴CG=PC=,PG=PC=,
∴BG=BC﹣CG=3﹣=,
在Rt△BPG中,由勾股定理可得BP==,
即BP的值为.
本题考查的是平行四边形的综合运用,熟练掌握平行四边形的性质和菱形的性质是解题的关键.
16、y=2x﹣1.
【解析】
设一次函数的解析式是:y=kx+b,把(3,-5)与(-4,9)代入即得到一个关于k,b的方程组,解方程组即可求解.
【详解】
解:设一次函数为
因为它的图象经过,
所以 解得:
所以这个一次函数为
本题考查了待定系数法求函数的解析式,正确解方程组是关键.
17、(1)DE=BC;(2)
【解析】
(1)由∠ACB=90°,∠A=30°得到∠B=60°,根据直角三角形斜边上中线性质得到DB=DC,则可判断△DCB为等边三角形,由于DE⊥BC,可得DE=BD=BC;
(2)根据旋转的性质得到∠PDF=60°,DP=DF,易得∠CDP=∠BDF,则可根据“SAS”判断△DCP≌△DBF,则CP=BF,利用CP+BP =BC,DE=BC可得到DE =(BF+BP).
【详解】
解:(1)∵∠ACB=90°,∠A=30°,
∴∠B=60°,
∵点D是AB的中点,
∴DB=DC,
∴△DCB为等边三角形,
∵DE⊥BC,
∴DE=BC;
故答案为DE=BD=BC.
(2)DE =(BF+BP).理由如下:
∵线段DP绕点D逆时针旋转60°,得到线段DF,
∴∠PDF=60°,DP=DF,
而∠CDB=60°,
∴∠CDB-∠PDB=∠PDF-∠PDB,
∴∠CDP=∠BDF,
在△DCP和△DBF中
,
∴△DCP≌△DBF(SAS),
∴CP=BF,
而CP=BC-BP,
∴BF+BP=BC,
∵DE=BC,
∴DE =(BF+BP);
故答案为DE =(BF+BP).
本题考查了全等三角形的判定与性质:判定三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”;全等三角形的对应边相等.也考查了等边三角形的判定与性质以及含30度的直角三角形三边的关系.
18、(1)6-t,+t;(2)①直线DE的解析式为:y=-;②
【解析】
(1)由O(1,1),A(6,1),C(1,3),可得:OA=6,OC=3,根据矩形的对边平行且相等,可得:AB=OC=3,BC=OA=6,进而可得点B的坐标为:(6,3),然后根据E点与F点的运动速度与运动时间即可用含t的代数式表示OE,OF;
(2)①由翻折的性质可知:△OPF≌△DPF,进而可得:DF=OF,然后由t=1时,DF=OF=,CF=OC-OF=,然后利用勾股定理可求CD的值,进而可求点D和E的坐标;利用待定系数可得直线DE的解析式;
②先确定出k的值,再分情况计算S的表达式,并确认b的取值.
【详解】
(1)∵O(1,1),A(6,1),C(1,3),
∴OA=6,OC=3,
∵四边形OABC是矩形,
∴AB=OC=3,BC=OA=6,
∴B(6,3),
∵动点F从O点以每秒1个单位长的速度沿OC向终点C运动,运动秒时,动点E从点A出发以相等的速度沿AO向终点O运动,
∴当点E的运动时间为t(秒)时,
AE=t,OF=+t,
则OE=OA-AE=6-t,
故答案为:6-t,+t;
(2)①当t=1时,OF=1+=,OE=6-1=5,则CF=OC-OF=3-=,
由折叠可知:△OEF≌△DEF,
∴OF=DF=,
由勾股定理,得:CD=1,
∴D(1,3);
∵E(5,1),
∴设直线DE的解析式为:y=mx+n(k≠1),
把D(1,3)和E(5,1)代入得:,解得:,
∴直线DE的解析式为:y=-;
②∵MN∥DE,
∴MN的解析式为:y=-,
当y=3时,-=3,x=(b-3)=b-4,
∴CM=b-4,
分三种情况:
i)当M在边CB上时,如图2,
∴BM=6-CM=6-(b-4)=11-b,
DM=CM-1=b-5,
∵1≤DM<5,即1≤b-5<5,
∴≤b<,
∴S=BM•AB=×3(11−b)=15-2b=-2b+15(≤b<);
ii)当M与点B重合时,b=,S=1;
iii)当M在DB的延长线上时,如图3,
∴BM=CM-6=b-11,
DM=CM-1=b-5,
∵DM>5,即b-5>5,
∴b>,
∴S=BM•AB=×3(b−11)=2b-15(b>);
综上,.
本题是四边形和一次函数的综合题,考查了动点的问题、矩形的性质、全等三角形的判定与性质等知识,解(1)的关键是:明确动点的时间和速度;解(2)的关键是:由翻折的性质可知:△OEF≌△DEF,并采用了分类讨论的思想,注意确认b的取值范围.
一、填空题(本大题共5个小题,每小题4分,共20分)
19、2021
【解析】
先根据平方差公式对分式进行化简,再将 代入即可得到答案.
【详解】
==(a+2),将代入得原式=2019+2=2021.
本题考察平方差公式和分式的化简,解题的关键是掌握平方差公式和分式的化简.
20、 (-3,1)
【解析】
直接利用已知点坐标得出原点的位置进而得出答案.
【详解】
解:如图所示:“兵”的坐标为:(-3,1).
故答案为(-3,1).
本题考查坐标确定位置,正确得出原点位置是解题关键.
21、-
【解析】
将分子变形为﹣(x﹣y),再约去分子、分母的公因式x﹣y即可得到结论.
【详解】
==﹣.
故答案为﹣.
本题主要考查分式的约分,由约分的概念可知,要首先将分子、分母转化为乘积的形式,再找出分子、分母的最大公因式并约去,注意不要忽视数字系数的约分.
22、
【解析】
本题是把实际问题转化为解直角三角形问题,由题意,已知DA=200,∠CDB=30°,CB:AB=1:0.5,∠CBD=90°,求CB.设AB=x,则CB=2x,由三角函数得:=tan30°,即=,求出x,从求出CB.即求出山的高度.
解:已知山坡AC的坡度i=1:0.5,
∴设AB=x,则CB=2x,又某人在D处测得山顶C的仰角为30°,即,∠CDB=30°,
∴=tan30°,即=,
解得:x=,
∴CB=2x=,
故答案为.
23、
【解析】
由从九年级(1)、(2)、(3)班中随机抽取一个班与九年级(4)班进行一场拔河比赛,有三种取法,其中抽到九年级(1)班的有一种,所以恰好抽到九年级(1)班的概率是:.
故答案为
二、解答题(本大题共3个小题,共30分)
24、(1)享受9折优惠的概率为;(2)顾客享受8折优惠的概率为.
【解析】
(1)由转动转盘甲共有四种等可能结果,其中指针指向A区域只有1种情况,利用概率公式计算可得;
(2)画树状图得出所有等可能结果,从中确定指针指向每个区域的字母相同的结果数,利用概率公式计算可得.
【详解】
(1)若选择方式一,转动转盘甲一次共有四种等可能结果,其中指针指向A区域只有1种情况,
∴享受9折优惠的概率为;
(2)画树状图如下:
由树状图可知共有12种等可能结果,其中指针指向每个区域的字母相同的有2种结果,
所以指针指向每个区域的字母相同的概率,即顾客享受8折优惠的概率为=.
本题考查的是用列表法或画树状图法求概率.注意列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.用到的知识点为:概率所求情况数与总情况数之比.
25、7200元
【解析】
仔细分析题目,需要求得四边形的面积才能求得结果.连接BD,在直角三角形ABD中可求得BD的长,由BD、CD、BC的长度关系可得三角形DBC为一直角三角形,DC为斜边;由此看,四边形ABCD由Rt△ABD和Rt△DBC构成,则容易求解.
【详解】
连接BD,
在Rt△ABD中,BD2=AB2+AD2=32+42=52,
在△CBD中,CD2=132,BC2=122,
而122+52=132,
即BC2+BD2=CD2,
∴∠DBC=90°,
S四边形ABCD=S△BAD+S△DBC=⋅AD⋅AB+DB⋅BC=×4×3+×12×5=36.
所以需费用36×200=7200(元).
此题考查勾股定理的应用,解题关键在于作辅助线和利用勾股定理进行计算.
26、(1)FC=3;(2)EF的长为5.
【解析】
(1)由折叠性质可得AF=AD,由勾股定理可求出BF的值,再由FC=BC-BF求解即可;
(2)由题意得EF=DE,设DE的长为x,则EC的长为(9-x)cm,在Rt△EFC中,由勾股定理即可求得EF的值.
【详解】
解:(1)∵矩形对边相等,
∴AD=BC=15
∵折叠长方形的一边AD,点D落在BC边上的点F处
∴AF=AD=15,
在Rt△ABF中,由勾股定理得,
∴FC=BC·BF=15-12=3
(2)折叠长方形的一边AD,点D落在BC边上的点F处
∴EF=DE
设DE=x,则EC=9·x,
在Rt△EFC中,由勾股定理得,
即
解得x=5
即EF的长为5。
本题主要考查了折叠问题,解题的关键是熟记折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.
题号
一
二
三
四
五
总分
得分
批阅人
浙江省杭州市上城区杭州中学2024年九上数学开学调研模拟试题【含答案】: 这是一份浙江省杭州市上城区杭州中学2024年九上数学开学调研模拟试题【含答案】,共24页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2025届浙江省杭州下城区九上数学开学调研模拟试题【含答案】: 这是一份2025届浙江省杭州下城区九上数学开学调研模拟试题【含答案】,共23页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2025届浙江省杭州上城区七校联考九上数学开学综合测试模拟试题【含答案】: 这是一份2025届浙江省杭州上城区七校联考九上数学开学综合测试模拟试题【含答案】,共27页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












