



- 【考点清单】专题08+导数及其应用-高二数学下学期期末考点大串讲试卷(人教B版2019选择性必修第三册) 试卷 0 次下载
- 【考题猜想】专题01 排列组合及其应用常考题型归类-高二数学下学期期末考点大串讲试卷(人教B版2019选择性必修第二册) 试卷 0 次下载
- 【考题猜想】专题02 二项式定理及其应用常考题型归类-高二数学下学期期末考点大串讲试卷(人教B版2019选择性必修第二册) 试卷 0 次下载
- 【考题猜想】专题03 条件概率与事件独立性常考题型归类-高二数学下学期期末考点大串讲试卷(人教B版2019选择性必修第二册) 试卷 0 次下载
- 【考题猜想】专题04 随机变量及其分布类常考题型归类-高二数学下学期期末考点大串讲试卷(人教B版2019选择性必修第二册) 试卷 0 次下载
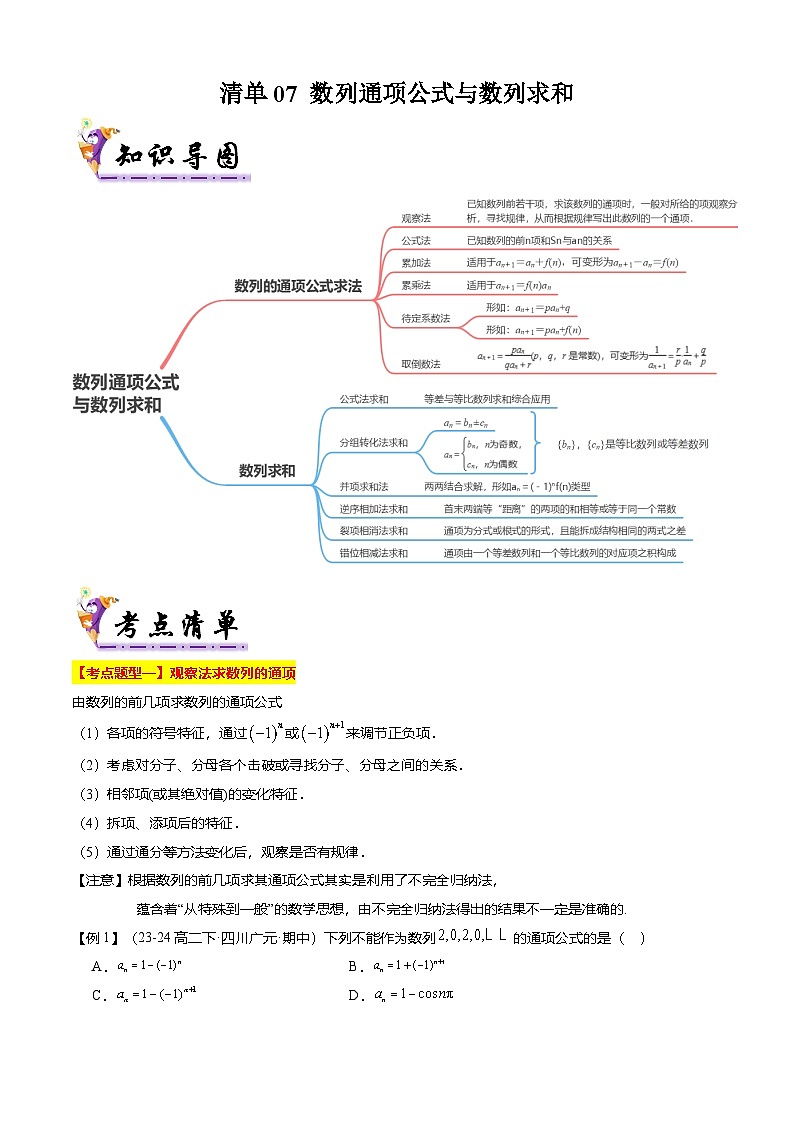
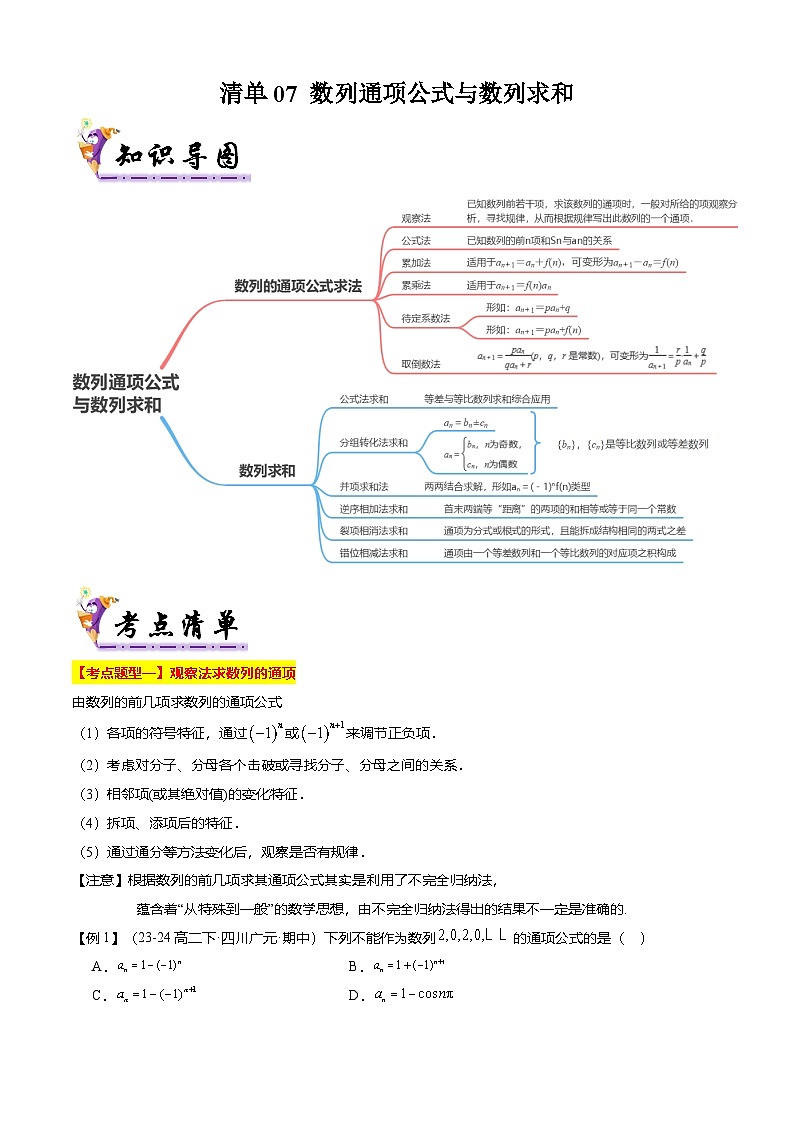
【考点清单】专题07+数列通项公式与数列求和-高二数学下学期期末考点大串讲试卷(人教B版2019选择性必修第三册)
展开【考点题型一】观察法求数列的通项
由数列的前几项求数列的通项公式
(1)各项的符号特征,通过或来调节正负项.
(2)考虑对分子、分母各个击破或寻找分子、分母之间的关系.
(3)相邻项(或其绝对值)的变化特征.
(4)拆项、添项后的特征.
(5)通过通分等方法变化后,观察是否有规律.
【注意】根据数列的前几项求其通项公式其实是利用了不完全归纳法,
蕴含着“从特殊到一般”的数学思想,由不完全归纳法得出的结果不一定是准确的.
【例1】(23-24高二下·四川广元·期中)下列不能作为数列的通项公式的是( )
A.B.
C.D.
【答案】C
【解析】A选项:通项为的数列,前4项分别为,,,,成立;
B选项:通项为,列出前面几项,也成立;
C选项:通项为的数列的第1项为,不成立;
D选项:通项为的数列,前4项分别为
,,,,成立.故选:C.
【变式1-1】(23-24高二下·吉林长春·期中)数列,3,,9的一个通项公式是( )
A.B.
C.D.
【答案】B
【解析】数列各项可改写为:,
因此一个通项公式可为=.故选:B.
【变式1-2】(23-24高二下·北京·期中)数列的前四项依次是4,44,444,4444,则数列的通项公式可以是( )
A.B.C.D.
【答案】C
【解析】根据题意,数列的前四项依次是:4,44,444,4444,
则有,,,,
则数列的通项公式可以是,故选:C.
【变式1-3】(23-24高二下·辽宁大连·月考)数列的通项公式为( )
A.B.
C.D.
【答案】D
【解析】根据数列的特点,归纳可得其通项公式为:.故选:D.
【考点题型二】由Sn与an的关系求数列通项
已知求的三个步骤:
(1)先利用求出.
(2)用替换中的得到一个新的关系,利用便可求出当时的表达式.
(3)对时的结果进行检验,看是否符合时的表达式,
如果符合,则可以把数列的通项公式合写;
如果不符合,则应该分与两段来写.
【例2】(23-24高二下·广东惠州通·月考)设数列的前项和为,若,则( )
A.65B.127C.129D.255
【答案】B
【解析】时,,则.
时,,
,
是2为首项,2为公比的等比数列,,故选:B.
【变式2-1】(23-24高二下·河北衡水·月考)已知为等比数列的前项和,,则( )
A.12B.24C.48D.96
【答案】C
【解析】由题知可得,
当时,,
所以,且,
由于为等比数列,可知,解得,
所以, .故选:C
【变式2-2】(23-24高二下·辽宁·期中)已知数列满足,则( )
A.B.C.D.
【答案】A
【解析】由 ① 知,
当时,;
当时, ②,
由① ② :,即得,
当时,符合题意,故.故选:A.
【变式2-3】(23-24高二下·吉林长春·期中)已知数列是正项数列,且,则( )
A.216B.260C.290D.316
【答案】A
【解析】令,得,∴.
当时,.
与已知式相减,得.
∴,
又时,满足上式,∴.
∴,∴.故选:A
【考点题型三】累加法求数列通项
若an+1−an=f(n),则an−an−1=f(n−1);an−1−an−2=f(n−2)……,a3−a2=f2,a2−a1=f1
两边分别相加得:an−a1=f1+f2+⋯+f(n−1)
【例3】(2024·陕西咸阳·三模)在数列中,,,则( )
A.43B.46C.37D.36
【答案】C
【解析】法一:由题得 ,
所以.
法二:由题,,
所以.故选:C.
【变式3-1】(23-24高二下·宁夏吴忠·月考)已知数列首项为,且,则( )
A.B.C.D.
【答案】C
【解析】由数列首项为,且,
则.故选:C.
【变式3-2】(23-24高二下·河南·月考)已知数列满足,则( )
A.B.C.D.
【答案】A
【解析】由已知得:,
又,所以,即,
所以是以为首项,为公比的等比数列,
因此,
当时,
相加得:.故选:A.
【变式3-3】(23-24高二下·四川成都·期中)已知数列满足,,则等于( )
A.B.C.D.
【答案】D
【解析】由题意,得,
则当时,,,,,
以上各式相加得,,
所以,即,
当时,适合此式,所以.故选:D.
【考点题型四】累乘法求数列通项
若an+1an=fn,则anan−1=fn−1,an−1an−2=fn−2,……,a3a2=f2,a2a2=f1,
两边分别相乘得:ana1=f1∙f(2)∙f(3)⋯f(n−1)
【例4】(23-24高二下·河南南阳·月考)已知数列满足,,则( )
A.B.C.D.
【答案】B
【解析】故选:B
【变式4-1】(23-24高二上·福建福州·期末)已知首项为1的数列,且对任意正整数恒成立,则数列的前项和为( )
A.B.C.D.
【答案】C
【解析】由题意易知,
由变形为,故,
所以
,
因为,所以,故,
所以.故选:C
【变式4-2】(23-24高三上·河南·期中)在数列中,,,,则( )
A.B.15C.D.10
【答案】B
【解析】因为,所以,即,得.
所以.
因为,所以.故选:B.
【变式4-3】(22-23高二下·广东佛山·期中)已知是数列的前项和,,,则的通项公式为( )
A.B.
C.D.
【答案】B
【解析】由得,
两式相减得: ,
即,即,即,.
所以,,,…,.
相乘得:……,
即,因为,所以,.
当时,,所以.故选:B
【考点题型五】待定系数法求数列通项
1、形如(为常数,且)的递推式,可构造,转化为等比数列求解.也可以与类比式作差,由,构造为等比数列,然后利用叠加法求通项.
2、形如 ,)的递推式,当时,两边同除以转化为关于的等差数列;当时,两边人可以同除以得,转化为.
3、形如,通过配凑转化为,通过待定系数法确定的值,转化成以为首项,以为公比的等比数列,再利用等比数列的通项公式求出的通项整理可得
【例5】(23-24高二上·河北石家庄·期末)设数列满足,则( )
A.B.C.D.
【答案】D
【解析】数列中,由,得,而,
因此数列是首项为1,公比为的等比数列,
,即,所以.故选:D
【变式5-1】(23-24高二下·广东佛山·月考)已知数列满足,且,若,则( )
A.253B.506C.1012D.2024
【答案】B
【解析】因为,所以.
因为,所以,故为常数列,
所以. 由,解得.故选:B
【变式5-2】(23-24高二下·河南周口·月考)已知数列为等比数列,为数列的前项和,,则的值为( )
A.9B.21C.45D.93
【答案】C
【解析】由得,整理得,
又得,
故数列是以为首项,2为公比的等比数列,
所以,即
所以.故选:C.
【变式5-3】(22-23高二下·江西萍乡·期末)已知正项数列中,,则数列的通项( )
A.B.C.D.
【答案】D
【解析】解法一:在递推公式的两边同时除以,得①,
令,则①式变为,即,
所以数列是等比数列,其首项为,公比为,
所以,即,
所以,
所以,
解法二:设,则,
与比较可得,
所以,
所以数列是首项为,公比为2的等比数列,
所以,所以,故选:D
【考点题型六】取倒数法求数列通项
对于,取倒数得.
当时,数列是等差数列;
当时,令,则,可用待定系数法求解.
【例6】(23-24高二上·湖北黄冈·月考)已知数列满足递推关系:,,则( )
A.B.C.D.
【答案】C
【解析】依题意,,由,得,即,而,
因此数列是以2为首项,1为公差的等差数列,
则,,
所以.故选:C
【变式6-1】(23-24高二上·福建龙岩·期中)已知数列满足,且,则( )
A.B.C.D.
【答案】B
【解析】,则,,,…,,
以上各式相加可得,,.故选:B
【变式6-2】(23-24高二上·浙江杭州·期末)若数列满足递推关系式,且,则( )
A.B.C.D.
【答案】A
【解析】因为,所以,所以,
又,所以,故数列是以为首项,以为公差的等差数列,
则,得,
所以.故选:A
【变式6-3】(23-24高二下·吉林长春·期中)已知数列中,且,则( )
A.B.C.D.
【答案】D
【解析】由得:,
又,数列是以1为首项,为公差的等差数列,
,
,,,故选:D.
【考点题型七】公式法求和
(1)等差数列的前n项和,推导方法:倒序相加法.
(2)等比数列的前n项和,推导方法:乘公比,错位相减法.
(3)一些常见的数列的前n项和:
①;
②;
③;
= 4 \* GB3 \* MERGEFORMAT ④
【例7】(23-24高二下·四川成都·期中)等差数列中,,.
(1)求的通项公式;
(2)设,记为数列前项的和,若,求.
【答案】(1);(2)
【解析】(1)设的公差为,由题设得
因为,所以,解得,故.
(2)由(1)得,因为,,
所以数列是以3为首项,3为公比的等比数列,
所以,
由得,解得.
【变式7-1】(23-24高二下·北京顺义·期中)已知数列是公差为的等差数列,数列是公比为的等比数列,且,,.
(1)求数列和的通项公式;
(2)求数列的前项和的最值;
(3)设,求数列的前项和.
【答案】(1),;(2),没有最大值;(3)
【解析】(1)因为数列是公差为的等差数列,数列是公比为的等比数列,
且,,即,
所以公差,则,所以,
又因为,,即,
所以公比,所以;
(2)数列的前项和,
所以或时,取得最小值,且,没有最大值;
(3)由(1)可得,
所以的前项和.
【变式7-2】(23-24高二下·北京·期中)在等差数列中,,.
(1)求数列的首项和公差;
(2)设数列的前n项和为,求的最小值及取最小值时n的值.
【答案】(1),;(2)最小值为,此时或.
【解析】(1)设等差数列的公差为,
因为,,可得,记得,
所以数列的首项为,公差为.
(2)由(1)知,可得,
因为,所以或时,取得最小值.
【变式7-3】(23-24高二下·陕西西安·月考)(1)已知数列满足,,求.
(2)等比数列的前项和为,已知、、成等差数列.
(i)求的公比;
(ii)若,求.
【答案】(1)(2)(i);(ii)
【解析】(1)因为,所以,又,
所以,则;
(2)(i)因为、、成等差数列,所以,
即,
因为,所以,解得或(舍去);
(ii)因为且,即,解得,
所以.
【考点题型八】分组转化法求和
(1)适用范围:某些数列的求和是将数列转化为若干个可求和的新数列的和或差,从而求得原数列的和,注意在含有字母的数列中对字母的讨论.
(2)常见类型:
= 1 \* GB3 ①若an=bn±cn,且{bn},{cn}为等差或等比数列;
= 2 \* GB3 ②通项公式为an=eq \b\lc\{(\a\vs4\al\c1(bn,n为奇数,,cn,n为偶数))的数列,其中数列{bn},{cn}是等比数列或等差数列.
【例8】(23-24高二下·四川达州·期中)已知数列是公差不为零的等差数列,满足,且成等比数列.
(1)求数列的通项公式;
(2)设,求数列的前项和.
【答案】(1);(2)
【解析】(1)设数列的公差为,由已知有
,即,解得(舍),
,;
(2),
.
【变式8-1】(23-24高二下·广东江门·月考)在递增等比数列中,,,数列的前n项和为,.
(1)求,的通项公式;
(2)求数列的前n项和.
【答案】(1),;(2)
【解析】(1)在递增等比数列中,,,解得,
设公比为,则,又因为为递增数列,故,
所以,所以,即;
数列的前n项和为,,
当时,,
则,
当时,,符合上式,
所以.
(2)由(1)知,,所以,
则
,
即.
【变式8-2】(23-24高二上·河北衡水·期末)在数列中,,且.
(1)若,证明:数列是等比数列;
(2)求数列的前项和.
【答案】(1)证明见解析;(2)
【解析】(1),
因为,所以是以为首项,为公比的等比数列;
(2)由(1)可知,所以,
所以
.
【变式8-3】(23-24高二上·贵州毕节·期末)已知递增的等比数列满足,且成等差数列.
(1)求的通项公式;
(2)设求数列的前项和.
【答案】(1);(2)
【解析】(1)由题意,设等比数列的公比为,
则,
成等差数列,
,即,
化简整理,得,解得(舍去),或,
首项,
.
(2)由(1)可得
则数列的前项和为
【考点题型九】并项法求和
并项求和法:一个数列的前n项和中,可两两结合求解,则称之为并项求和.形如an=(-1)nf(n)类型,可采用两项合并求解.
例如,.
【例9】(23-24高二下·陕西西安·月考)在数列中,已知,则的值为?
【答案】
【解析】因为,
当为偶数时
,
当为奇数时
,
所以,,,
所以.
【变式9-1】(23-24高二下·广东佛山·期中)设是等差数列,是公比大于0的等比数列,已知,,.
(1)求和的通项公式;
(2)设,求数列的前项和.
【答案】(1),;(2)
【解析】(1)设等差数列的公差为d,等比数列的公比为q,且.
依题意得,解得,所以或.
又因为,所以,所以,
故,.
(2),
.
【变式9-2】(23-24高二下·广东佛山·月考)已知数列满足.
(1)求证:数列是等差数列,并求数列的通项公式;
(2)若,求数列的前项和.
【答案】(1)证明见解析,;(2)
【解析】(1)显然,将两边同时取倒数得,即,
所以数列是公差为2的等差数列,
所以,所的.
(2)由已知得,那么数列的前项和,
当为偶数时,;
当为奇数时,.
故.
【变式9-3】(23-24高二上·山东青岛·期末)已知等差数列的前项和为,公差为,且成等比数列,.
(1)求数列的通项公式;
(2)若,求数列的前30项的和.
【答案】(1);(2)
【解析】(1)依题意,则,解得,
则,故,
所以,解得,则,
故.
(2),
,
.
【考点题型十】逆序相加法求和
倒序相加法:如果一个数列{an}的前n项中首末两端等“距离”的两项的和相等或等于同一个常数,那么求这个数列的前n项和即可用倒序相加法,如等差数列的前n项和公式即是用此法推导的.
【例10】(23-24高二下·北京·期中)已知,,则数列的通项公式为( )
A.B.C.D.
【答案】A
【解析】,
则
两式相加得
所以,所以.故选:A.
【变式10-1】(23-24高二下·云南文山·月考)函数,则的值为( ).
A.2012B.C.2013D.
【答案】B
【解析】由可得:,
所以,,
所以设
,
则两式相加可得:
故选:B.
【变式10-2】(23-24高二下·辽宁大连·期中)已知数列是公比为的正项等比数列,且,若,则( )
A.4050B.2025C.4052D.2026
【答案】A
【解析】由数列是公比为的正项等比数列,故,
因为,故,
即有,
由,则当时,有,
设,
,
,,
故.故选:.
【变式10-3】(23-24高二下·辽宁沈阳·月考)德国大数学家高斯年少成名,被誉为数学界的王子.在其年幼时,对的求和运算中,提出了倒序相加法的原理,该原理基于所给数据前后对应项的和呈现一定的规律生成.因此,此方法也称为高斯算法.现有函数,则的值为 .
【答案】1009
【解析】由函数,得,
令,
则,
两式相加得,解得,
所以所求值为1009.
【考点题型十一】裂项相消法求和
1、用裂项法求和的裂项原则及规律
(1)裂项原则:一般是前边裂几项,后边就裂几项,直到发现被消去项的规律为止.
(2)消项规律:消项后前边剩几项,后边就剩几项,前边剩第几项,后边就剩倒数第几项.
【注意】利用裂项相消法求和时,既要注意检验通项公式裂项前后是否等价,又要注意求和时,正负项相消消去了哪些项,保留了哪些项,切不可漏写未被消去的项.
2、裂项相消法中常见的裂项技巧
(1) (2)
(3) (4)
(5) (6)
(7)
【例11】(23-24高二下·河南·月考)已知正项数列前项和为,且满足,.
(1)求数列的通项公式;
(2)若数列满足,求数列的前项和.
【答案】(1)();(2)
【解析】(1)∵①,
当,时,有②,
由①-②得,即,
∵正项数列,,∴,,
∴数列是首项为2,公差为3的等差数列,
∴().
(2)由(1)得,
则(),
∴.
【变式11-1】(23-24高二下·广东佛山·期中)已知数列的首项,前项和为,且,.
(1)证明:数列为等差数列,并求的通项公式;
(2)设数列,求数列的前项和.
【答案】(1)证明见解析,;(2)
【解析】(1)因为,所以,
因为,即,
故数列是以为首项,以为公差的等差数列,
所以,所以;
(2)由(1),
当时,,
所以,
又适合上式,所以,
所以,
所以.
【变式11-2】(23-24高二下·河北石家庄·月考)已知等差数列的前n项的和为成等差数列,且成等比数列.
(1)求的通项公式;
(2)若,数列的前n项的和为,试比较与的大小,并证明你的结论.
【答案】(1);(2),证明见解析
【解析】(1)设的公差为,由题意得,
即,解得,
所以.
(2),
所以,
因为,所以,即.
【变式11-3】(23-24高二下·河南·月考)已知数列满足.
(1)求的通项公式;
(2)若,记数列的前项和为,求证:.
【答案】(1);(2)证明见解析.
【解析】(1)因为,所以
又,所以,
所以是以9为首项,3为公比的等比数列,
所以,所以.
(2)由(1)知,
所以
,
又,所以.
【考点题型十二】错位相减法求和
1、解题步骤
2、注意解题“3关键”
①要善于识别题目类型,特别是等比数列公比为负数的情形.
②在写出“Sn”与“qSn”的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“Sn-qSn”的表达式.
③在应用错位相减法求和时,若等比数列的公比为参数,应分公比q=1和q≠1两种情况求解.
3、等差乘等比数列求和,令,可以用错位相减法.
①
②
得:.
整理得:.
【例12】(23-24高二下·重庆·期中)已知等差数列的前项和为,且,.
(1)求数列的通项公式以及前项和;
(2)若,求数列的前项和.
【答案】(1),;(2)
【解析】(1)设等差数列的公差为,
由,得,解得,
所以,
所以;
(2)由(1)可得,
所以,
则,
所以
,
所以.
【变式12-1】(23-24高二下·山东潍坊·期中)在数列中,(是常数,),且成公比不为1的等比数列.
(1)求的值;
(2)求数列的通项公式:
(3)求数列的前项和.
【答案】(1);(2);(3)
【解析】(1),,,
因为成公比不为1的等比数列,
所以,解得或.
当时,,不符合题意舍去,故.
(2)当时,由于,
所以,
又,故.
当时,满足上式,所以.
(3)因为,
所以,
,
两式相减得
即.
【变式12-2】(23-24高二下·广东佛山·月考)已知数列满足,,数列的前项和为,且.
(1)求,的通项公式;
(2)求数列的前项和.
【答案】(1),;(2)
【解析】(1)因为,,
所以当时,,得.
当时,,
所以,所以.
因为时也满足,
所以,所以,所以.
因为,所以当时,,解得.
当时,,所以,所以,
所以是首项为,公比为的等比数列,故.
(2)由(1)可得,
所以,
,
两式相减得
,
所以.
【变式12-3】(23-24高二下·江西南昌·期中)已知数列的通项公式为,在与中插入个数,使这个数组成一个公差为的等差数列,记数列的前项和为,
(1)求的通项公式及;
(2)设,为数列的前项和,求.
【答案】(1),;(2)
【解析】(1)因为在,之间插入项,使这个数成公差为的等差数列,
所以,
所以.
(2)易知,所以,
两式相减得,
所以.
【考点题型十三】数列求和与不等式成立问题
数列与不等式是高考的热点问题,其综合的角度主要包括两个方面:
一是不等式恒成立或能成立条件下,求参数的取值范围:此类问题常用分离参数法,转化为研究最值问题来求解;二是不等式的证明:常用方法有比较法、构造辅助函数法、放缩法、数学归纳法等。
【例13】(2024·辽宁辽阳·一模)已知数列满足.
(1)求的通项公式;
(2)设,证明:.
【答案】(1);(2)证明见解析
【解析】(1)由题意可知,当时,;
当时,由得,,
两式作差可得,,
也适合该式,故;
(2)证明:由题意知,
故,
由于,则,故,
即.
【变式13-1】(23-24高二下·贵州铜仁·月考)已知数列的前n项和为,,,.
(1)求数列和的通项公式;
(2)记数列的前n项和为,若对任意都成立,求实数m的取值范围.
【答案】(1),;(2)
【解析】(1)当时,,当时,,
所以,化简得,
因为,所以数列是首项为,公比为的等比数列,
所以,所以.
(2)因为,
所以,由得,
因为对任意都成立,所以,解得,
故实数m的取值范围为.
【变式13-2】(23-24高二下·辽宁大连·期中)已知数列中,,设为前项和,,已知数列,设的前项和.
(1)求;
(2)若对任意恒成立,求实数的取值范围.
【答案】(1);(2).
【解析】(1)由可得:,,
上面两式相减得:,整理得:,,
所以数列是常数列,即,所以,则,
所以
两边同乘以2得:
两式相减得:,
即.
(2)由可得:,整理得:,
当为偶数时,上面不等式可化简为:,
利用该数列单调递增性可知:,所以,
当为奇数时,上面不等式可化简为:,
再利用该数列单调递减性可知:,所以,
综上可得:.
【变式13-3】(23-24高二下·江苏南京·月考)已知数列的前项和满足.
(1)求的通项公式;
(2)设数列满足,记数列的前项和为,若存在使得成立,求的取值范围.
【答案】(1);(2)
【解析】(1),当时,,
当,时,,,
两式相减得:为非零定值,而,
即是以1为首项,公比的等比数列,所以;
(2),
所以,
,
两式相减:,
由得,,即存在使成立,
随着增大,在减小,当时,,
故求的取值范围是.
【考点题型十四】数列中的探究性问题
数列中的探究性问题实际上就是不定方程解的问题,对于此类问题的求解,通常有以下三种常用的方法:①利用等式两边的整数是奇数还是偶数的方法来加以判断是否存在;②利用寻找整数的因数的方法来进行求解;③通过求出变量的取值范围,从而对范围内的整数值进行试根的方法来加以求解.对于研究不定方程的解的问题,也可以运用反证法,反证法证明命题的基本步骤:
①反设:设要证明的结论的反面成立.作反设时要注意把结论的所有反面都要写出来,不要有遗漏.②归谬:从反设出发,通过正确的推理得出与已知条件或公理、定理矛盾的结论.③存真:否定反设,从而得出原命题结论成立.
【例14】(2023·广东·模拟预测)记为数列的前项和,已知的等差中项为.
(1)求证为等比数列;
(2)数列的前项和为,是否存在整数满足?若存在求,否则说明理由.
【答案】(1)证明见解析;(2)存在,
【解析】(1)因为的等差中项为,所以,
因为时,,则,所以,
由得,
又,两式相减得,即,
所以有,所以,
所以是等比数列,其首项为,公比为2.
(2)由(1)知,所以,所以,
因为,所以,
又,
所以,所以.
【变式14-1】(23-24高二下·黑龙江双鸭山·月考)数列满足:是等比数列,,且.
(1)求;
(2)求集合中所有元素的和;
(3)对数列,若存在互不相等的正整数,使得也是数列中的项,则称数列是“和稳定数列”.试分别判断数列是否是“和稳定数列”.若是,求出所有的值;若不是,说明理由.
【答案】(1),;(2)
(3)数列是“和稳定数列”,,数列不是“和稳定数列”,理由见解析
【解析】(1),
又,,解得:
因为是等比数列,所以的公比,
又当时,,
作差得:
将代入,化简:,得:
是公差的等差数列,
(2)记集合的全体元素的和为,
集合的所有元素的和为,
集合的所有元素的和为,
集合的所有元素的和为,则有
对于数列:
当时,是数列中的项
当时,不是数列中的项
,其中
即(其中表示不超过实数的最大整数)
(3)①当时,是的正整数倍,
故一定不是数列中的项;
当时,,不是数列中的项;
当时,,是数列中的项;
综上,数列是“和稳定数列”,;
②数列不是“和稳定数列”,理由如下:
不妨设:,则,且
故不是数列中的项.
数列不是“和稳定数列”.
【变式14-2】(23-24高二下·广东佛山·期中)已知数列满足,是公差为的等差数列.
(1)求的通项公式.
(2)令,求数列的前n项和.
(3)令,是否存在互不相等的正整数m,s,n,使得m,s,n成等差数列,且,,成等比数列?如果存在,请给出证明;如果不存在,请说明理由.
【答案】(1);(2);(3)不存在,理由见解析
【解析】(1)由已知得,且,则,
所以,所以,解得.
(2)由(1)知,所以.
.
(3)由题意可知.
假设存在,则,且,
即,则有,
化简得,将代入,即得.
因为,当且仅当时,等号成立.
又因为m,n,s互不相等,所以不存在.
【变式14-3】(23-24高二下·江苏连云港·期中)已知数列的前项和为,且满足:,.
(1)求数列的通项公式;
(2)设,求数列的前项和;
(3)设数列的通项公式为,问:是否存在正整数,使得成等差数列?若存在,求出和的值;若不存在,请说明理由.
【答案】(1);(2);(3)存在,,取值见解析.
【解析】(1)由①,当时,,
当时,②,
①-②得,即,
所以,所以,
当时,,上式也成立,
所以数列为常数列,,所以.
(2)由,,
则,
所以的前项和为.
(3)由(1)知.
要使成等差数列,则,
即,整理得,
因为,为正整数,所以只能取2,3,5.
当时,;
当时,;
当时,.
故存在正整数,使得成等差数列.
【考点清单】专题06+等差数列与等比数列-高二数学下学期期末考点大串讲试卷(人教B版2019选择性必修第三册): 这是一份【考点清单】专题06+等差数列与等比数列-高二数学下学期期末考点大串讲试卷(人教B版2019选择性必修第三册),文件包含考点清单专题06等差数列与等比数列16题型解读原卷版docx、考点清单专题06等差数列与等比数列16题型解读解析版docx等2份学案配套教学资源,其中学案共44页, 欢迎下载使用。
【考点清单】专题04+随机变量的均值与方差综合-高二数学下学期期末考点大串讲试卷(人教B版2019选择性必修第二册): 这是一份【考点清单】专题04+随机变量的均值与方差综合-高二数学下学期期末考点大串讲试卷(人教B版2019选择性必修第二册),文件包含考点清单专题04随机变量的均值与方差综合9题型解读原卷版docx、考点清单专题04随机变量的均值与方差综合9题型解读解析版docx等2份学案配套教学资源,其中学案共29页, 欢迎下载使用。
【考点清单】专题03+随机变量的分布列-高二数学下学期期末考点大串讲试卷(人教B版2019选择性必修第二册): 这是一份【考点清单】专题03+随机变量的分布列-高二数学下学期期末考点大串讲试卷(人教B版2019选择性必修第二册),文件包含考点清单专题03随机变量的分布列11题型解读原卷版docx、考点清单专题03随机变量的分布列11题型解读解析版docx等2份学案配套教学资源,其中学案共42页, 欢迎下载使用。












