2024-2025学年北京市西城区育才学校高二（上）月考数学试卷（10月份）（含答案）

这是一份2024-2025学年北京市西城区育才学校高二（上）月考数学试卷（10月份）（含答案），共8页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
一、单选题：本题共10小题，每小题4分，共40分。在每小题给出的选项中，只有一项是符合题目要求的。
1.已知a=(2,−1,3)，b=(−4,2,x)，且a⊥b，则x=( )
A. 103B. −6C. 6D. 1
2.直线x+y−1=0的倾斜角为( )
A. 45°B. 135°C. 90°D. 120°
3.已知空间向量a=(0,2,0)，b=(1,0,−1)，则(a+b)⋅b=( )
A. −2B. −1C. 1D. 2
4.在空间直角坐标系中，点P(1,2,−3)关于坐标平面xOy的对称点为( )
A. (−1,−2,3)B. (−1,−2,−3)C. (−1,2,−3)D. (1,2,3)
5.若a=(x,−1,3)，b=(2,y,6)，且a//b，则( )
A. x=1，y=2B. x=1，y=−2
C. x=12，y=−2D. x=−1，y=−2
6.如图，在正方体ABCD−A1B1C1D1中，E为CD的中点，则直线A1E与BB1C1C所成角的正弦值为( )
A. 25 B. 35
C. 13 D. 23
7.在棱长为1的正方体ABCD−A1B1C1D1中，E为A1D1的中点，则点C1到直线CE的距离为( )
A. 13B. 33C. 53D. 63
8.如图，空间四边形OABC中，OA=a，OB=b，OC=c，点M是OA的中点，点N在BC上，且CN=2NB，设MN=xa+yb+zc，则x，y，z的值为( )
A. 12 , 13, 23 B. 12 , 23, 13
C. −12 , 23, 13 D. −12 , 13, 23
9.已知在棱长均为2的正三棱柱ABC−A1B1C1中，点D为B1C1的中点，若在棱AB上存在一点P，使得B1P//平面ACD，则B1P的长度为( )
A. 2B. 5C. 6D. 3
10.如图，在正方体ABCD−A1B1C1D1中，点E是侧面BB1C1C内的一个动点，若点E满足D1E⋅CE=0，则点E的轨迹为( )
A. 圆
B. 半圆
C. 直线
D. 线段
二、填空题：本题共5小题，每小题4分，共20分。
11.已知向量a=(1,2,2),b=(3,2,0)，则|a−b|= ______．
12.已知点A(−2,0,−2)，B(−1,6,−8)，AB的中点坐标为______．
13.如图，以长方体ABCD−A1B1C1D1的顶点D为坐标原点，过D的三条棱所在的直线为坐标轴，建立空间直角坐标系，若DB1的坐标为(4,3,2)，则AC1的坐标是______．
14.正四棱锥所有棱长均为2，则侧面与底面所成二面角的正切值为______．
15.棱长为1的正方体ABCD−A1B1C1D1中，若点P为线段A1B上的动点(不含端点)，则下列结论正确的是______．
①平面A1D1P⊥平面AA1P
②四面体D1−B1CP的体积是定值
③△APD1可能是钝角三角形
④直线D1P与AB所成的角可能为π6
三、解答题：本题共4小题，共40分。解答应写出文字说明，证明过程或演算步骤。
16.(本小题10分)
在长方体ABCD−A1B1C1D1中，AB=3，AD=AA1=2，点E在AB上，且AE=1．
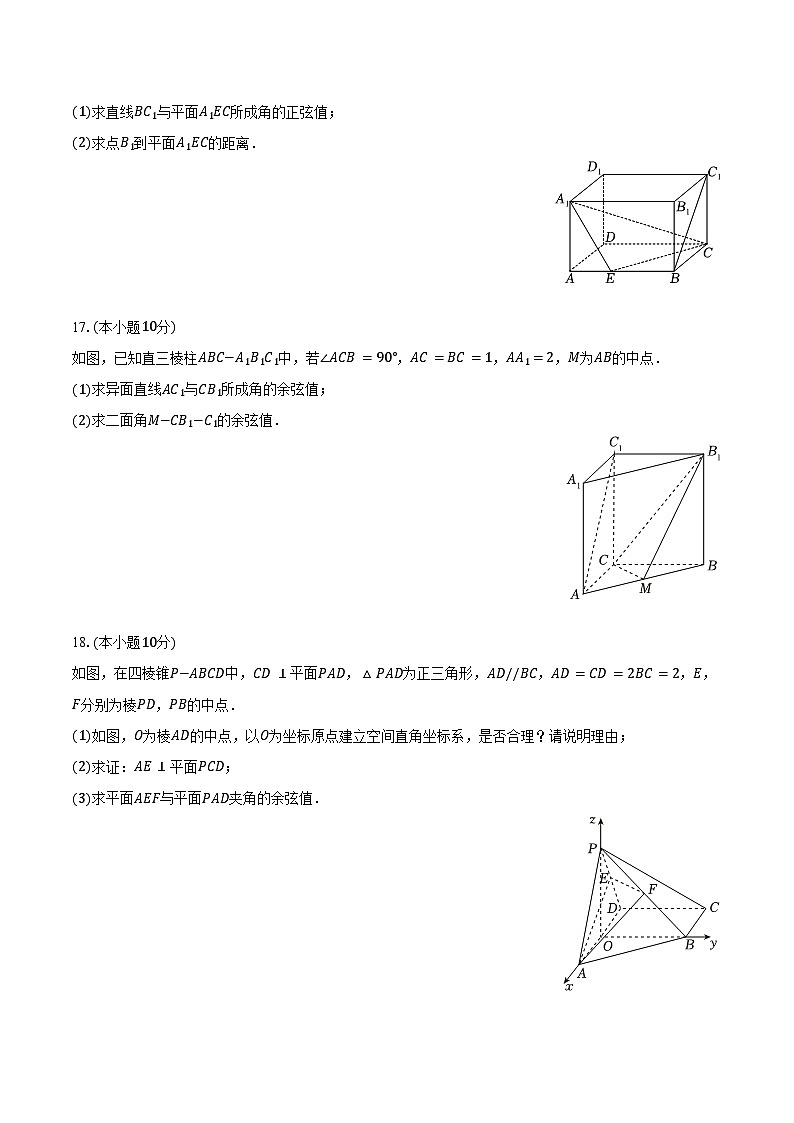
(1)求直线BC1与平面A1EC所成角的正弦值；
(2)求点B1到平面A1EC的距离．
17.(本小题10分)
如图，已知直三棱柱ABC−A1B1C1中，若∠ACB=90°，AC=BC=1，AA1=2，M为AB的中点．
(1)求异面直线AC1与CB1所成角的余弦值；
(2)求二面角M−CB1−C1的余弦值．
18.(本小题10分)
如图，在四棱锥P−ABCD中，CD⊥平面PAD，△PAD为正三角形，AD//BC，AD=CD=2BC=2，E，F分别为棱PD，PB的中点．
(1)如图，O为棱AD的中点，以O为坐标原点建立空间直角坐标系，是否合理？请说明理由；
(2)求证：AE⊥平面PCD；
(3)求平面AEF与平面PAD夹角的余弦值．
19.(本小题10分)
如图，在四棱锥P−ABCD中，PD⊥底面ABCD，底面ABCD为菱形，且AB=2，∠DAB=60°，点M为棱DP的中点．
(1)在棱BC上是否存在一点N，使得CM//平面PAN？如果存在，确定点N的位置，如果不存在，请并说明理由；
(2)若二面角B−CM−D的余弦值为 66时，求棱DP的长度，并求点A到平面BCM的距离．
参考答案
1.A
2.B
3.D
4.D
5.B
6.C
7.C
8.C
9.B
10.B
11.2 2
12.(−32,3,−5)
13.(−4,3,2)
14. 2
15.①②③
16.解：(1)以D为坐标原点，DA，DC，DD1所在直线分别为x，y，z轴，建立如图所示空间直角坐标系，

则A1(2,0,2)，E(2,1,0)，B(2,3,0)，C1(0,3,2)，C(0,3,0)，B1(2,3,2)，
可得A1E=(0,1,−2)，BC1=(−2,0,2)，EC=(−2,2,0)，
设平面A1EC的法向量为n=(x,y,z)，
则n⋅A1E=y−2z=0n⋅EC=−2x+2y=0，
令z=1，则x=y=2，可得n=(2,2,1)，
可得|cs|=|n⋅BC1||n||BC1|=|−4+2|3×2 2= 26，
所以直线BC1与平面A1EC所成角的正弦值为 26；
(2)由(1)可得：EB1=(0,2,2)，
所以B1到平面A1EC的距离为|n⋅B1E||n|=63=2..
17.解：(1)由题意，在直三棱柱ABC−A1B1C1中，∠ACB=90°，
则可以C为坐标原点，建立如图所示的空间直角坐标系，

由AC=BC=1，AA1=2，M为AB的中点，
可得A(1,0,0)，C(0,0,0)，M(12,12,0)，B1(0,1,2)，C1(0,0,2)，
则AC1=(−1,0,2)，CB1=(0,1,2)，
故cs=AC1⋅CB1|AC1||CB1|=4 5× 5=45，
即异面直线AC1与CB1所成角的余弦值为45；
(2)由(1)知，CM=(12,12,0)，CB1=(0,1,2)，
设平面MCB1的一个法向量为n=(x,y,z)，
则有n⋅CM=12x+12y=0n⋅CB1=y+2z=0，令x=2，可得y=−2，z=1，
可得平面MCB1的一个法向量为n=(2,−2,1)，
不妨取平面CB1C1的一个法向量为m=(1,0,0)，
则cs=m⋅n|m||n|=2 9×1=23，
由图可知，二面角M−CB1−C1为钝角，
故二面角M−CB1−C1的余弦值为−23．
18.解：(1)因为△PAD为正三角形，O为AD中点，则PO⊥AD，
又AD//BC，AD=2BC，O为棱AD的中点，
所以BO/​/CD，又CD⊥平面PAD，
所以BO⊥平面PAD，由OD，OP⊂平面PAD，
故OB，OD，OP两两垂直，
所以以O为坐标原点建立的空间直角坐标系合理；
(2)证明：因为CD⊥平面PAD，AD⊂平面PAD，AE⊂平面PAD，
所以CD⊥AD，CD⊥AE，
又因为△PAD为等边三角形，E为PD的中点，
所以PD⊥AE，又PD∩CD=D，
所以AE⊥平面PCD；
(3)由题意，A(0,0,0)，E(−12,0, 32)，F(0,1, 32)，
B(0,2,0)，P(0,0, 3)，D(−1,0,0)，
则AE=(−32,0, 32)，EF=(12,1,0)，
设平面AEF的一个法向量为n=(x,y,z)，
则有n⋅AE=0n⋅EF=0，即−32x+ 32z=012x+y=0，
令x=2，可得平面AEF的一个法向量n=(2,−1,2 3)，
易知平面PAD的一个法向量为OB=(0,2,0)，
则cs=OB⋅n|OB||n|=−22× 4+1+12=− 1717，
所以平面AEF与平面PAD夹角的余弦值为 1717．
19.解：(1)在棱BC上存在点N，使得CM/​/平面PAN，点N为棱BC的中点．证明如下：
取PA的中点Q，连结NQ、MQ，
由题意，MQ//AD且MQ=12AD，CN/​/AD且CN=12AD，
故CN//MQ且CN=MQ．
∴四边形CNQM为平行四边形．
∴CM//NQ，又CM⊄平面PAN，NQ⊂平面PAN，∴CM/​/平面PAN．

(2)因为PD⊥平面ABCD，又∠DAB=60°，底面ABCD为菱形，
所以△ABD为正三角形，
取AB中点E，连接DE，
则DE⊥AB，也即DE⊥DC，
所以DE，DC，DP两两互相垂直，
以D为坐标原点，分别以DE，DC，DP所在直线为x，y，z轴建立空间直角坐标系，
设MD=a，则D(0,0,0)，M(0,0,a)，C(0,2,0)，B( 3,1,0)，A( 3,−1,0)，
所以MC=(0,2,−a)，CB=( 3,−1,0)，
设平面MBC的一个法向量为m=(x,y,z)，
由m⋅AC=2y−az=0m⋅CB= 3x−y=0，
取x=1，得m=(1, 3,2 3a)，
取平面DMC的一个法向量为n=(1,0,0)，
由题意得 66=|cs〈m,n〉|=1 1+3+12a2，
解得a= 6，故DP=2DM=2a=2 6，
所以MA=( 3,−1,− 6)，
设点A到平面BCM的距离为d，
则d=|m⋅MA||m|=2 3 6= 2，
即点A到平面BCM的距离为 2．