江苏省靖江市生祠初级中学2024年九年级数学第一学期开学复习检测模拟试题【含答案】

这是一份江苏省靖江市生祠初级中学2024年九年级数学第一学期开学复习检测模拟试题【含答案】，共24页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）下列各组数中能作为直角三角形的三边长的是（ ）．
A．1，，1B．2，3，4C．4，5，6D．8，13，5
2、（4分）平行四边形不一定具有的性质是（ ）
A．对角线互相垂直B．对边平行且相等C．对角线互相平分D．对角相等
3、（4分）某同学五天内每天完成家庭作业的时间（时）分别为2，3，2，1，2，则对这组数据的下列说法中错误的是（ ）
A．平均数是2B．众数是2C．中位数是2D．方差是2
4、（4分）一个一元一次不等式的解集在数轴上表示如图所示，则该不等式的解集为（ ）
A．x≥2B．x＜2C．x＞2D．x≤2
5、（4分）如图，、两处被池塘隔开，为了测量、两处的距离，在外选一点，连接、，并分别取线段、的中点、，测得，则的长为（ ）
A．B．C．D．
6、（4分）甲袋装有4个红球和1个黑球，乙袋装有6个红球、4个黑球和5个白球．这些球除了颜色外没有其他区别，分别搅匀两袋中的球，从袋中分别任意摸出一个球，正确说法是（ ）
A．从甲袋摸到黑球的概率较大
B．从乙袋摸到黑球的概率较大
C．从甲、乙两袋摸到黑球的概率相等
D．无法比较从甲、乙两袋摸到黑球的概率
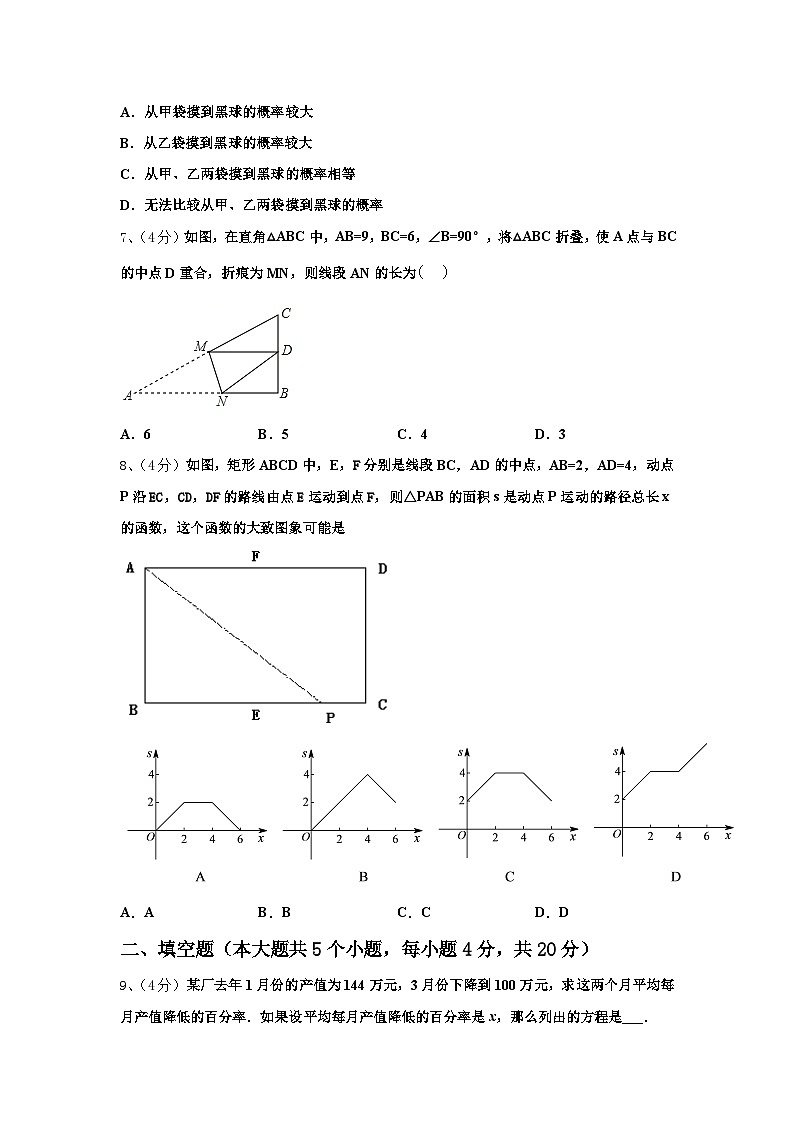
7、（4分）如图，在直角△ABC中，AB=9，BC=6，∠B=90°，将△ABC折叠，使A点与BC的中点D重合，折痕为MN，则线段AN的长为
A．6B．5C．4D．3
8、（4分）如图，矩形ABCD中，E，F分别是线段BC，AD的中点，AB=2，AD=4，动点P沿EC，CD，DF的路线由点E运动到点F，则△PAB的面积s是动点P运动的路径总长x的函数，这个函数的大致图象可能是
A．AB．BC．CD．D
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）某厂去年1月份的产值为144万元，3月份下降到100万元，求这两个月平均每月产值降低的百分率．如果设平均每月产值降低的百分率是x，那么列出的方程是___．
10、（4分）比较大小：2____3(填“ ＞、＜、或 = ”).
11、（4分）如果从初三(1)、(2)、(3)班中随机抽取一个班与初三(4)班进行一场拔河比赛，那么恰好抽到初三(1)班的概率是_____．
12、（4分）如图，将矩形ABCD的四个角向内翻折后，恰好拼成一个无缝隙无重叠的四边形EFGH，EH=6cm，GH=8cm，则边AB的长是__________
13、（4分）当m＝_____时，x2+2（m﹣3）x+25是完全平方式.
三、解答题（本大题共5个小题，共48分）
14、（12分）将矩形ABCD绕点B顺时针旋转得到矩形A1BC1D1，点A、C、D的对应点分别为A1、C1、D1
（1）当点A1落在AC上时
①如图1，若∠CAB＝60°，求证：四边形ABD1C为平行四边形；
②如图2，AD1交CB于点O．若∠CAB≠60°，求证：DO＝AO；
（2）如图3，当A1D1过点C时．若BC＝5，CD＝3，直接写出A1A的长．
15、（8分）如图，是边长为2的等边三角形，将沿直线平移到的位置，连接．
（1）求平移的距离；
（2）求的长．
16、（8分）正方形的对角线相交于点，点又是正方形的一个顶点，而且这两个正方形的边长相等.试证明：无论正方形绕点怎样转动，两个正方形重叠部分的面积，总等于一个正方形面积的.
17、（10分）如图，正比例函数与反比例函数的图像交于A，B两点，过点A作AC⊥x轴，垂足为C，△ACO的面积为1．
（1）求反比例函数的表达式；
（2）点B的坐标为 ；
（3）当时，直接写出x的取值范围．
18、（10分）正方形ABCD中，点E是BD上一点，过点E作EF⊥AE交射线CB于点F，连结CE．
（1）已知点F在线段BC上．
①若AB=BE，求∠DAE度数；
②求证：CE=EF；
（2）已知正方形边长为2，且BC=2BF，请直接写出线段DE的长．
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）如图，已知直线l1：y=k1x+4与直线l2：y=k2x﹣5交于点A，它们与y轴的交点分别为点B，C，点E，F分别为线段AB、AC的中点，则线段EF的长度为______．
20、（4分）在函数中，自变量的取值范围是__________.
21、（4分）如图，正比例函数y＝ax的图象与反比例函数y＝的图象相交于点A，B，若点A的坐标为(－2,3)，则点B的坐标为_________．
22、（4分）矩形ABCD中，对角线AC、BD交于点O，于，若，，则____.
23、（4分）平面直角坐标系中，A、O两点的坐标分别为（2，0），（0，0），点P在正比例函数y＝x（x＞0）图象上运动，则满足△PAO为等腰三角形的P点的坐标为_____．
二、解答题（本大题共3个小题，共30分）
24、（8分）如图，正方形ABCD中，E、F分别是AB、BC边上的点，且AE=BF，求证：AF⊥DE．
25、（10分）在学校组织的八年级知识竞赛中，每班参加比赛的人数相同，成绩分为、、、四个等级，其中相应等级的得分依次记为100分、90分、80分、70分，学校将一班和二班的成绩整理并绘制成如下的统计图：
请你根据以上提供的信息解答下列问题：
（1）求一班参赛选手的平均成绩；
（2）此次竞赛中，二班成绩在级以上（包括级）的人数有几人？
（3）求二班参赛选手成绩的中位数．
26、（12分）在中，，是边上的中线，是的中点，过点作交的延长线于点，连接．
（1）如图1，求证：
（2）如图2，若，其它条件不变，试判断四边形的形状，并证明你的结论．
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、A
【解析】
根据勾股定理的逆定理对各选项进行逐一分析即可．
【详解】
A选项：，故可以构成直角三角形；
B选项：，故不能构成直角三角形；
C选项：，故不能构成直角三角形；
D选项：，故不能构成直角三角形；
故选：A．
考查的是勾股定理的逆定理，熟知如果三角形的三边长a，b，c满足a2+b2=c2，那么这个三角形就是直角三角形是解答此题的关键．
2、A
【解析】
结合平行四边形的性质即可判定。
【详解】
结合平行四边形的性质可知选项B、C、D均正确，但平行四边形的对角线不垂直，则A不正确.
故选A．
本题考查了平行四边形的性质，熟练掌握平行四边形的性质是正确解题的关键。
3、D
【解析】
根据众数、中位数、平均数和方差的计算公式分别进行解答，即可得出答案．
【详解】
解：平均数是：（2+3+2+1+2）÷5＝2；
数据2出现了3次，次数最多，则众数是2；
数据按从小到大排列：1，2，2，2，3，则中位数是2；
方差是：[（2﹣2）2+（3﹣2）2+（2﹣2）2+（1﹣2）2+（2﹣2）2]＝，
则说法中错误的是D；
故选D．
本题考查众数、中位数、平均数和方差，平均数表示一组数据的平均程度．中位数是将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（或最中间两个数的平均数）；方差是用来衡量一组数据波动大小的量；众数是一组数据中出现次数最多的数．
4、D
【解析】
直接将解集在数轴上表示出来即可，注意实心和空心的区别
【详解】
数轴上读出不等式解集为x≤2，故选D
本题考查通过数轴读出不等式解集，属于简单题
5、C
【解析】
根据题意直接利用三角形中位线定理，可求出.
【详解】
、是、的中点，
是的中位线，
，
，
.
故选.
本题考查的是三角形的中位线定理在实际生活中的运用，锻炼了学生利用几何知识解答实际问题的能力.
6、B
【解析】
试题分析：根据概率的计算法则可得：甲袋P（摸到黑球）=；乙袋P（摸到黑球）=.根据可得：从乙袋摸到黑球的概率较大.
考点：概率的计算
7、B
【解析】
设，由翻折的性质可知，则，在中利用勾股定理列方程求解即可．
【详解】
解：设，由翻折的性质可知，则．
是BC的中点，
．
在中，由勾股定理得：，即，
解得：．
．
故选：B．
本题主要考查的是翻折的性质、勾股定理的应用，由翻折的性质得到，，从而列出关于x的方程是解题的关键．
8、C
【解析】
分点P在EC、CD、DF上运动，根据三角形面积公式进行求解即可得.
【详解】
当点P在EC上运动时，此时0≤x≤2，PB=2+x，则S△PAB==×2（2+x）=x+2；
当点P在CD运动时，此时2当点P在DF上运动时，此时4观察选项，只有C符合，
故选C.
本题考查了动点问题的函数图象，分情况求出函数解析式是解题的关键.
二、填空题（本大题共5个小题，每小题4分，共20分）
9、144（1﹣x）2＝1．
【解析】
设平均每月产值降低的百分率是x，那么2月份的产值为144（1-x）万元，3月份的产值为144（1-x）2万元，然后根据3月份的产值为1万元即可列出方程．
【详解】
设平均每月产值降低的百分率是x，则2月份的产值为144（1﹣x）万元，3月份的产值为144（1﹣x）2万元，
根据题意，得144（1﹣x）2＝1．
故答案为144（1﹣x）2＝1．
本题考查由实际问题抽象出一元二次方程-求平均变化率的方法．若设变化前的量为a，变化后的量为b，平均变化率为x，则经过两次变化后的数量关系为a（1±x）2=b．得到3月份的产值的等量关系是解决本题的关键．
10、＜
【解析】
试题分析：将两式进行平方可得：=12，=18，因为12＜18，则＜.
11、
【解析】
由从九年级（1）、（2）、（3）班中随机抽取一个班与九年级（4）班进行一场拔河比赛，有三种取法，其中抽到九年级（1）班的有一种，所以恰好抽到九年级（1）班的概率是：．
故答案为
12、．
【解析】
利用三个角是直角的四边形是矩形易证四边形EFGH为矩形，那么由折叠可得GE的长，进而求出HM，AB即为边2HM的长．
【详解】
解：∵∠HEM=∠HEB，∠GEF=∠CEF，∴∠HEF=∠HEM+∠GEF=∠BEG+∠GEC=×180°=90°，
同理可得：∠EHG=∠HGF=∠EFG=90°，
∴四边形EFGH为矩形，
∵EH=6cm，GH=8cm，
∴GE=10
由折叠可知，HM⊥GE，AH=HM，BH=HM，
∵，
∴AB＝AH+BH＝2HM＝2×＝．
故答案为．
此题主要考查了翻折变换的性质以及勾股定理等知识，得出四边形EFGH为矩形是解题关键．
13、8或﹣1
【解析】
先根据两平方项确定出这两个数，再根据完全平方公式的乘积二倍项即可确定m的值．
【详解】
解：∵x1+1（m﹣3）x+15＝x1+1（m﹣3）x+51，
∴1（m﹣3）x＝±1×5x，
m﹣3＝5或m﹣3＝﹣5，
解得m＝8或m＝﹣1．
故答案为：8或﹣1．
本题主要考查了完全平方式，根据平方项确定出这两个数是解题的关键，也是难点，熟记完全平方公式对解题非常重要．
三、解答题（本大题共5个小题，共48分）
14、（1）①证明见解析；②证明见解析；（2）
【解析】
（1）①首先证明△ABA1是等边三角形，可得∠AA1B＝∠A1BD1＝60°，即可解决问题．
②首先证明△OCD1≌△OBA（AAS），推出OC＝OB，再证明△DCO≌△ABO（SAS）即可解决问题．
（2）如图3中，作A1E⊥AB于E，A1F⊥BC于F．利用勾股定理求出AE，A1E即可解决问题．
【详解】
（1）证明：①如图1中，
∵∠BAC＝60°，BA＝BA1，
∴△ABA1是等边三角形，
∴∠AA1B＝60°，
∵∠A1BD1＝60°，
∴∠AA1B＝∠A1BD1，
∴AC∥BD1，
∵AC＝BD1，
∴四边形ABD1C是平行四边形．
②如图2中，连接BD1．
∵四边形ABD1C是平行四边形，
∴CD1∥AB，CD1＝AB，
∠OCD1＝∠ABO，
∵∠COD1＝∠AOB，
∴△OCD1≌△OBA（AAS），
∴OC＝OB，
∵CD＝BA，∠DCO＝∠ABO，
∴△DCO≌△ABO（SAS），
∴DO＝OA．
（2）如图3中，作A1E⊥AB于E，A1F⊥BC于F．
在Rt△A1BC中，∵∠CA1B＝90°，BC＝2．AB＝3，
∴CA1＝＝4，
∵•A1C•A1B＝•BC•A1F，
∴A1F＝，
∵∠A1FB＝∠A1EB＝∠EBF＝90°，
∴四边形A1EBF是矩形，
∴EB＝A1F＝，A1E＝BF＝，
∴AE＝3﹣＝，
在Rt△AA1E中，AA1＝＝．
本题属于四边形综合题，考查了矩形的性质，全等三角形的判断和性质，勾股定理，平行四边形的判定和性质等知识，解题的关键是灵活运用所学知识解决问题，学会添加常用辅助线，构造直角三角形解决问题．
15、（1）2；（2）
【解析】
（1）由平移的性质，即可得出平移距离；
（2）由平移的性质以及边长关系，可判定∠BAE=90°，利用勾股定理即可得解.
【详解】
（1）∵△DCE由△ABC平移而成
∴△ABC的平移距离为BC=2；
（2）由平移，得
BE=2BC=4，AB=AC=CE
∵等边△ABC
∴∠BAC=∠ACB=60°
∴∠CAE=∠CEA=30°
∴∠BAE=∠BAC+∠CAE=60°+30°=90°
∴.
此题主要考查等边三角形、平移的性质以及勾股定理的运用，熟练掌握，即可解题.
16、见解析.
【解析】
分两种情况讨论：（1）当正方形边与正方形的对角线重合时；（2）当转到一般位置时，由题求证，故两个正方形重叠部分的面积等于三角形的面积，得出结论.
【详解】
（1）当正方形绕点转动到其边，分别于正方形的两条对角线重合这一特殊位置时，
显然；
（2）当正方形绕点转动到如图位置时，
∵四边形为正方形，
∴，，，即
又∵四边形为正方形，
∴，即，
∴，
在和中，
，
∴，
∵，
又，
∴.
此题考查正方形的性质，三角形全等的判定与性质，三角形的面积等知识点.
17、解： ；
（2）B（-2，-1）；
（3）-22.
【解析】
（1）根据反比例函数图象的性质，反比例函数上任意一点向x轴（或y轴）作垂线，这一点、所交点与原点之间所围成的直角三角形的面积等于 ，图象经过一、三象限k>0；
（2）联立正比例函数与反比例函数，解出的x，y分别为交点的横、纵坐标，这里需注意解得的解集有两个，说明交点有两个，需要考虑点所在位于哪一个象限；
（3）观察图像可以解决问题，谁的图像在上面，谁对应的函数值大，这里需过两个交点作x轴垂线，两条垂线与y轴将图象分成四部分，分别讨论.
【详解】
解：（1）∵△ACO的面积为1，C⊥x轴
∴,
即,
∵点A是函数的点
∴，
∵反比例函数的图像在第一、三象限，
∴k>0
∴k=8,反比例函数表达式为 ；
（2）联立 ，可解得 或，
∵B点在第三象限，
∴点B坐标为（-2，-1）.
（3）根据（2）易得A点坐标为（2,1），
所以当-22时，
（1）考查反比例函数图象的性质问题，图中△ACO的面积正好是，图象在第一、三象限，所以k>0；
（2）考查函数交点问题，两个函数的交点的横、纵坐标分别是联立它们，所形成的方程组的解集对应的x、y值；
（3）可借助图象比较两个函数的大小，这里一定要注意分不同区间去考虑.
18、（1）①22.5°；②证明见解析；（2）或．
【解析】
(1)①先求得∠ABE的度数，然后依据等腰三角形的性质和三角形内角和定理求得∠BAE的度数，然后可求得∠DAE度数；
②先利用正方形的对称性可得到∠BAE=∠BCE，然后在证明又∠BAE=∠EFC，通过等量代换可得到∠BCE=∠EFC；
(2)当点F在BC上时，过点E作MN⊥BC，垂直为N，交AD于M.依据等腰三角形的性质可得到FN=CN，从而可得到NC的长，然后可得到MD的长，在Rt△MDE中可求得ED的长；当点F在CB的延长线上时，先根据题意画出图形，然后再证明EF=EC，然后再按照上述思路进行解答即可．
【详解】
(1)①∵ABCD为正方形，∴∠ABE=45°，
又∵AB=BE，∴∠BAE(180°﹣45°)=67.5°，
∴∠DAE=90°﹣67.5°=22.5°；
②∵正方形ABCD关于BD对称，
∴△ABE≌△CBE，∴∠BAE=∠BCE，
又∵∠ABC=∠AEF=90°，∴∠BAE=∠EFC，∴∠BCE=∠EFC，∴CE=EF；
(2)如图1，过点E作MN⊥BC，垂直为N，交AD于M，
∵CE=EF，∴N是CF的中点，
∵BC=2BF，∴，
又∵四边形CDMN是矩形，△DME为等腰直角三角形，
∴CN=DM=ME，
∴EDDMCN；
如图2，过点E作MN⊥BC，垂直为N，交AD于M，
∵正方形ABCD关于BD对称，∴△ABE≌△CBE，∴∠BAE=∠BCE，
又∵∠ABF=∠AEF=90°，∴∠BAE=∠EFC，
∴∠BCE=∠EFC，∴CE=EF，∴FN=CN，
又∵BC=2BF，∴FC=3，∴CN，∴EN=BN，∴DE，
综上所述：ED的长为或.
本题考查了正方形的性质、全等三角形的性质和判定、等腰三角形的性质和判定、等腰直角三角形的性质，正确添加辅助线并灵活运用相关知识是解本题的关键.
一、填空题（本大题共5个小题，每小题4分，共20分）
19、．
【解析】
根据直线方程易求点B、C的坐标，由两点间的距离得到BC的长度．所以根据三角形中位线定理来求EF的长度．
【详解】
解：∵直线l1：y=k1x+4，直线l2：y=k2x﹣5，
∴B（0，4），C（0，﹣5），
则BC=1．
又∵点E，F分别为线段AB、AC的中点，
∴EF是△ABC的中位线，
∴EF=BC=．
故答案是：．
20、x≠2
【解析】
根据分式有意义的条件进行求解即可.
【详解】
由题意得，2x-4≠0，
解得：x≠2，
故答案为：x≠2.
本题考查了函数自变量的取值范围，一般从三个方面考虑：(1)当函数表达式是整式时，自变量可取全体实数；(2)当函数表达式是分式时，考虑分式的分母不能为0；(3)当函数表达式是二次根式时，被开方数非负．
21、（2，﹣3）
【解析】
试题分析：反比例函数的图象是中心对称图形，则经过原点的直线的两个交点一定关于原点对称．
解：根据题意，知
点A与B关于原点对称，
∵点A的坐标是（﹣2，3），
∴B点的坐标为（2，﹣3）．
故答案是：（2，﹣3）．
点评：本题考查了反比例函数图象的中心对称性，关于原点对称的两点的横、纵坐标分别互为相反数．
22、1或
【解析】
试题解析：如图（一）所示，
AB是矩形较短边时，
∵矩形ABCD，
∴OA=OD=BD；
∵OE：ED=1：3，
∴可设OE=x，ED=3x，则OD=2x
∵AE⊥BD，AE=，
∴在Rt△OEA中，x2+（）2=（2x）2，
∴x=1
∴BD=1．
当AB是矩形较长边时，如图（二）所示，
∵OE：ED=1：3，
∴设OE=x，则ED=3x，
∵OA=OD，
∴OA=1x，
在Rt△AOE中，x2+（）2=（1x）2，
∴x=，
∴BD=8x=8×=．
综上，BD的长为1或.
23、（1，1）或（，）或（1，1）
【解析】
分OP＝AP、OP＝OA、AO＝AP三种情况考虑：①当OP1＝AP1时，△AOP1为等腰直角三角形，根据等腰直角三角形的性质结合点A的坐标可得出点P1的坐标；②当OP1＝OA时，过点P1作P1B⊥x轴，则△OBP1为等腰直角三角形，根据等腰直角三角形的性质结合点A的坐标可得出点P1的坐标；③当AO＝AP3时，△OAP3为等腰直角三角形，根据等腰直角三角形的性质结合点A的坐标可得出点P3的坐标．综上即可得出结论
【详解】
∵点A的坐标为（1，0），
∴OA＝1．
分三种情况考虑，如图所示．
①当OP1＝AP1时，∵∠AOP1＝45°，
∴△AOP1为等腰直角三角形．
又∵OA＝1，
∴点P1的坐标为（1，1）；
②当OP1＝OA时，过点P1作P1B⊥x轴，则△OBP1为等腰直角三角形．
∵OP1＝OA＝1，
∴OB＝BP1＝，
∴点P1的坐标为（，）；
③当AO＝AP3时，△OAP3为等腰直角三角形．
∵OA＝1，
∴AP3＝OA＝1，
∴点P3的坐标为（1，1）．
综上所述：点P的坐标为（1，1）或（，）或（1，1）．
故答案为：（1，1）或（，）或（1，1）．
本题考查了一次函数图象上点的坐标特征、等腰三角形的性质以及等腰直角三角形的性质，分OP＝AP、OP＝OA、AO＝AP三种情况求出点P的坐标是解题的关键．
二、解答题（本大题共3个小题，共30分）
24、证明见解析
【解析】
由题意先证明△ADE≌△BAF，得出∠EDA=∠FAB，再根据∠ADE+∠AED=90°，推得∠FAE+∠AED=90°，从而证出AF⊥DE．
【详解】
解：∵四边形ABCD为正方形，
∴DA=AB，∠DAE=∠ABF=90°，
又∵AE=BF，
∴△DAE≌△ABF，
∴∠ADE=∠BAF，
∵∠ADE+∠AED=90°，
∴∠FAE+∠AED=90°，
∴∠AGE=90°，
∴AF⊥DE．
本题考查正方形的性质；全等三角形的判定与性质．
25、（1）分；（2）人；（3）80分
【解析】
（1）根据算术平均数的定义列式计算可得；
（2）总人数乘以A、B、C等级所占百分比即可；
（3）根据中位数的定义求解即可．
【详解】
解：（1）一班参赛选手的（分）
（2）二班成绩在级以上（含级）（人）
（3）二班、人数占，
参赛学生共有20人，因此中位数落在C级，
二班参赛选手成绩的中位数为80分．
本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．
26、（1）见解析；（2）四边形为正方形，见解析
【解析】
（1）先证明得到AF=DB，于是可证；
（2）先证明四边形是平行四边形，再加一组邻边相等证明它是菱形，最后利用等腰三角形三线合一的性质证明有一个直角,从而证明它是正方形.
【详解】
（1）证明：∵是的中点
，
，
，
又，
，
，
是边上的中线 ，
，
；
（2）解：四边形为正方形，理由如下：
由（1）得，
又，
∴四边形为平行四边形，
在中，
是边上的中线，
，
∴四边形为菱形，
，是边上的中线，
∴四边形为正方形.
本题考查了正方形的判定，涉及的知识点有直角三角形斜边中线的性质，全等三角形的判定、平行四边形及菱形、正方形的判定，掌握相关性质定理进行推理论证是解题关键.
题号
一
二
三
四
五
总分
得分