河北省石家庄市同文中学2025届九年级数学第一学期开学教学质量检测模拟试题【含答案】

这是一份河北省石家庄市同文中学2025届九年级数学第一学期开学教学质量检测模拟试题【含答案】，共24页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）如图，在中，点D、E、F分别在边、、上，且，．下列四种说法： ①四边形是平行四边形；②如果，那么四边形是矩形；③如果平分，那么四边形是菱形；④如果且，那么四边形是菱形. 其中，正确的有（ ） 个
A．1B．2C．3D．4
2、（4分）下列四组线段中，能组成直角三角形的是
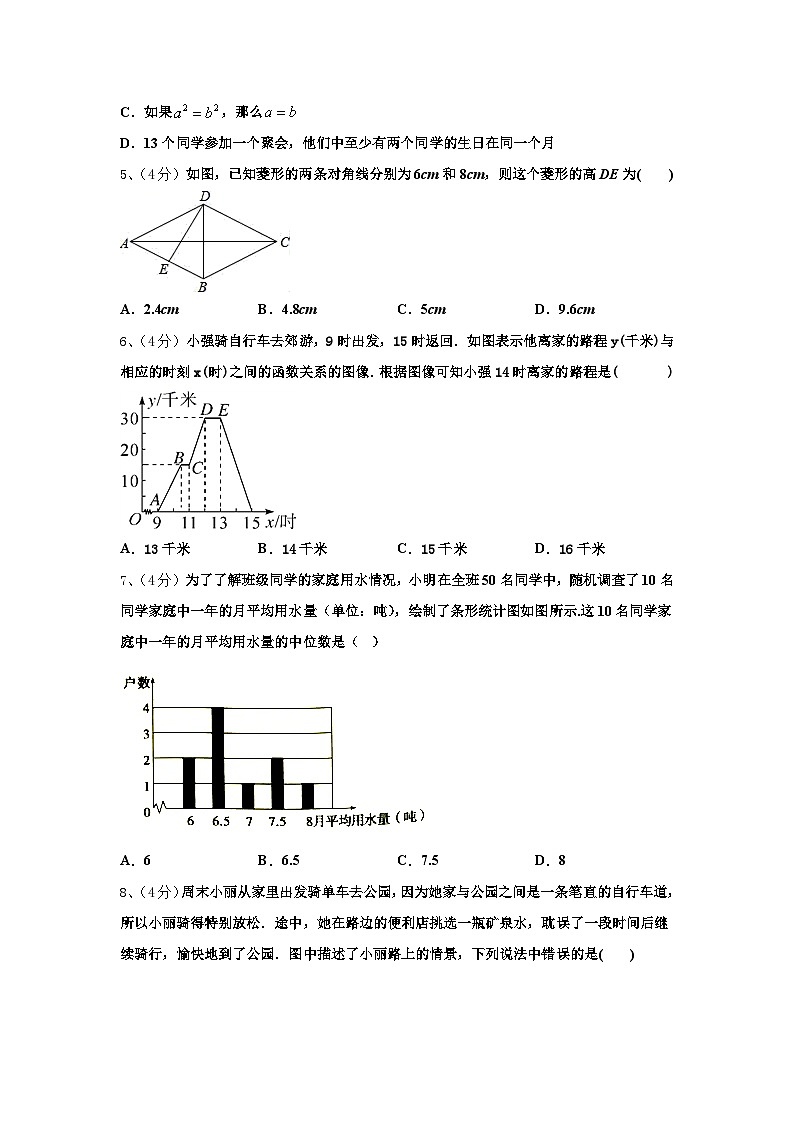
A．，，B．，，
C．，，D．，，
3、（4分）下列命题正确的是( )
A．在同一平面内，可以把半径相等的两个圆中的一个看成是由另一个平移得到的.
B．两个全等的图形之间必有平移关系.
C．三角形经过旋转，对应线段平行且相等.
D．将一个封闭图形旋转，旋转中心只能在图形内部.
4、（4分）下列事件中是必然事件的是（ ）
A．投掷一枚质地均匀的硬币100次，正面朝上的次数为50次
B．一组对边平行，另一组对边相等的四边形是等腰梯形
C．如果，那么
D．13个同学参加一个聚会，他们中至少有两个同学的生日在同一个月
5、（4分）如图，已知菱形的两条对角线分别为6cm和8cm，则这个菱形的高DE为( )
A．2.4cmB．4.8cmC．5cmD．9.6cm
6、（4分）小强骑自行车去郊游，9时出发，15时返回．如图表示他离家的路程y(千米)与相应的时刻x(时)之间的函数关系的图像．根据图像可知小强14时离家的路程是( )
A．13千米B．14千米C．15千米D．16千米
7、（4分）为了了解班级同学的家庭用水情况，小明在全班50名同学中，随机调查了10名同学家庭中一年的月平均用水量（单位：吨），绘制了条形统计图如图所示.这10名同学家庭中一年的月平均用水量的中位数是（ ）
A．6B．6.5C．7.5D．8
8、（4分）周末小丽从家里出发骑单车去公园，因为她家与公园之间是一条笔直的自行车道，所以小丽骑得特别放松．途中，她在路边的便利店挑选一瓶矿泉水，耽误了一段时间后继续骑行，愉快地到了公园．图中描述了小丽路上的情景，下列说法中错误的是( )
A．小丽从家到达公园共用时间20分钟B．公园离小丽家的距离为2000米
C．小丽在便利店时间为15分钟D．便利店离小丽家的距离为1000米
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）如图，已知▱OABC的顶点A、C分别在直线x=1和x=4上，O是坐标原点，则对角线OB长的最小值为__．
10、（4分）已知一组数据为1，2，3，4，5，则这组数据的方差为_____．
11、（4分）已知直线与平行且经过点，则的表达式是__________．
12、（4分）已知一次函数（）经过点，则不等式的解集为__________．
13、（4分）如图，矩形全等于矩形，点在上.连接，点为的中点.若，，则的长为__________．
三、解答题（本大题共5个小题，共48分）
14、（12分）某汽车销售公司6月份销售某厂家的汽车，在一定范围内，每部汽车的进价与销售有如下关系，若当月仅售出1部汽车，则该部汽车的进价为27万元，每多售一部，所有出售的汽车的进价均降低0.1万元/部．月底厂家根据销售量一次性返利给销售公司，销售量在10部以内，含10部，每部返利0.5万元，销售量在10部以上，每部返利1万元．
① 若该公司当月卖出3部汽车，则每部汽车的进价为万元；
② 如果汽车的销售价位28万元/部，该公司计划当月盈利12万元，那么要卖出多少部汽车？（盈利=销售利润+返利）
15、（8分）如图，直线是一次函数的图象．
（1）求出这个一次函数的解析式；
（2）将该函数的图象向下平移3个单位，求出平移后一次函数的解析式，并写出平移后的图像与轴的交点坐标
16、（8分）如图，在平面直角坐标系 xOy中，直线ykxb与 x轴相交于点A，与反比例函数在第一象限内的图像相交于点 A(1，8)、B(m，2)．
(1)求该反比例函数和直线y kxb的表达式；
(2)求证：ΔOBC为直角三角形；
(3)设∠ACO＝α，点Q为反比例函数在第一象限内的图像上一动点，且满足90°－α＜∠QOC＜α，求点Q的横坐标q的取值范围．

17、（10分）八年级班一次数学测验，老师进行统计分析时，各分数段的人数如图所示(分数为整数，满分分)．请观察图形，回答下列问题：
（1）该班有____名学生：
（2）请估算这次测验的平均成绩．
18、（10分）某学生本学期6次数学考试成绩如下表所示：
（1）6次考试成绩的中位数为 ，众数为 .
（2）求该生本学期四次月考的平均成绩.
（3）如果本学期的总评成绩按照月考平均成绩占20﹪、期中成绩占30﹪、期末成绩占50﹪计算，那么该生本学期的数学总评成绩是多少？
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）使有意义的x取值范围是＿＿＿＿＿＿．
20、（4分）在实数范围内定义一种运算“*”，其规则为a*b＝a2﹣b2，根据这个规则，方程（x+2）*5＝0的解为_____．
21、（4分）如图，OP平分∠MON，PE⊥OM于点E，PF⊥ON于点F，OA＝OB，则图中有____对全等三角形．
22、（4分）为了考察甲、乙两块地小麦的长势，分别从中随机抽出10株苗，测得苗高如图所示．若和 分别表示甲、乙两块地苗高数据的方差，则________．(填“>”、“<”或“=”)．
23、（4分）为了解当地气温变化情况，某研究小组记录了寒假期间连续6天的最高气温，结果如下（单位：℃）：－6，－3，x，2，－1，3，若这组数据的中位数是－1，在下列结论中：①方差是8；②极差是9；③众数是－1；④平均数是－1，其中正确的序号是________.
二、解答题（本大题共3个小题，共30分）
24、（8分）如图，中，是的中点，将沿折叠后得到，且 点在□内部．将延长交于点．
（1）猜想并填空：________（填“”、“”、“”）；
（2）请证明你的猜想；
（3）如图，当，设，，，证明：．
25、（10分）如图，在ABCD中，AD∥BC，AC＝BC＝4，∠D＝90°，M，N分别是AB、DC的中点，过B作BE⊥AC交射线AD于点E，BE与AC交于点F．
(1)当∠ACB＝30°时，求MN的长：
(2)设线段CD＝x，四边形ABCD的面积为y，求y与x的函数关系式及其定义域；
(3)联结CE，当CE＝AB时，求四边形ABCE的面积．
26、（12分）（1）解分式方程：
（2）解不等式组，并在数轴上表示其解集．
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、D
【解析】
先由两组对边分别平行的四边形为平行四边形，根据DE∥CA，DF∥BA，得出AEDF为平行四边形，得出①正确；当∠BAC=90°，根据推出的平行四边形AEDF，利用有一个角为直角的平行四边形为矩形可得出②正确；若AD平分∠BAC，得到一对角相等，再根据两直线平行内错角相等又得到一对角相等，等量代换可得∠EAD=∠EDA，利用等角对等边可得一组邻边相等，根据邻边相等的平行四边形为菱形可得出③正确；由AB=AC，AD⊥BC，根据等腰三角形的三线合一可得AD平分∠BAC，同理可得四边形AEDF是菱形，④正确，进而得到正确说法的个数．
【详解】
解：∵DE∥CA，DF∥BA，
∴四边形AEDF是平行四边形，选项①正确；
若∠BAC=90°，
∴平行四边形AEDF为矩形，选项②正确；
若AD平分∠BAC，
∴∠EAD=∠FAD，
又DE∥CA，∴∠EDA=∠FAD，
∴∠EAD=∠EDA，
∴AE=DE，
∴平行四边形AEDF为菱形，选项③正确；
若AB=AC，AD⊥BC，
∴AD平分∠BAC，
同理可得平行四边形AEDF为菱形，选项④正确，
则其中正确的个数有4个．
故选D．
此题考查了平行四边形的定义，菱形、矩形的判定，涉及的知识有：平行线的性质，角平分线的定义，以及等腰三角形的判定与性质，熟练掌握平行四边形、矩形及菱形的判定与性质是解本题的关键．
2、D
【解析】
由勾股定理的逆定理，只要验证两小边的平方和等于最长边的平方即可．
【详解】
A.1²+2²≠3²，故不是直角三角形，故本选项错误；
B.2²+3²≠4²故不是直角三角形，故本选项错误；
C.2²+4²≠5²，故不是直角三角形，故本选项错误；
D.3²+4²=5 ²，故是直角三角形，故本选项正确．
故选D．
本题考查勾股定理的逆定理的应用．判断三角形是否为直角三角形，已知三角形三边的长，只要利用勾股定理的逆定理加以判断即可．
3、A
【解析】
根据平移的性质：平移后图形的大小、方向、形状均不发生改变结合选项即可得出答案．
【详解】
解：A、经过旋转后的图形两个图形的大小和形状也不变，半径相等的两个圆是等圆，圆还具有旋转不变性，故本选项正确；
B、两个全等的图形位置关系不明确，不能准确判定是否具有平移关系，错误；
C、三角形经过旋转，对应线段相等但不一定平行，所以本选项错误；
D、旋转中心可能在图形内部，也可能在图形边上或者图形外面，所以本选项错误.
故选：A.
本题考查平移、旋转的基本性质，注意掌握①平移不改变图形的形状和大小；②经过平移，对应点所连的线段平行且相等，对应线段平行且相等，对应角相等．
4、D
【解析】
根据事件发生的可能性大小判断相应事件的类型即可．
【详解】
解：A、投掷一枚质地均匀的硬币100次，正面朝上的次数为50次是随机事件；
B、一组对边平行，另一组对边相等的四边形是等腰梯形是随机事件；
C、如果a2=b2，那么a=b是随机事件；
D、13个同学参加一个聚会，他们中至少有两个同学的生日在同一个月是必然事件；
故选：D．
本题考查的是必然事件、不可能事件、随机事件的概念．必然事件指在一定条件下，一定发生的事件．不可能事件是指在一定条件下，一定不发生的事件，不确定事件即随机事件是指在一定条件下，可能发生也可能不发生的事件．
5、B
【解析】
解：如图所示：
∵四边形ABCD是菱形，
∴OA=AC=4，OB=BD=3，AC⊥BD，
∴AB=，
∵菱形ABCD的面积=AB•DE=AC•BD=×8×6=24，
∴DE==4.8；
故选B．
6、C
【解析】
由纵坐标看出，返回时离家的距离是30千米，
由横坐标看出，返回时所用的时间是15−13=2小时，
由路程与时间的关系，得
返回时的速度是30÷2=15千米，
由时间、速度的关系得15×1=15千米，
故选：C.
7、B
【解析】
根据条形统计图，即可知道每一名同学家庭中一年的月均用水量，再根据中位数的概念进行求解
【详解】
解：：共有10个数据，
.中位数是第5、6个数据的平均数由条形图知第5、6个数据为6.5，6.5，
所以中位数为，
故选：B.
本题考查的是条形统计图的运用，读懂统计图，从统计图中得到必要的信息是解决问题的关键，注意掌握中位数的计算方法.
8、C
【解析】
解：A．小丽从家到达公园共用时间20分钟，正确；
B．公园离小丽家的距离为2000米，正确；
C．小丽在便利店时间为15﹣10=5分钟，错误；
D．便利店离小丽家的距离为1000米，正确．
故选C．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、1．
【解析】
试题分析：当B在x轴上时，对角线OB长的最小，如图所示：直线x=1与x轴交于点D，直线x=4与x轴交于点E，根据题意得：∠ADO=∠CEB=90°，OD=1，OE=4，∵四边形ABCD是平行四边形，∴OA∥BC，OA=BC，∴∠AOD=∠CBE，在△AOD和△CBE中，∵∠AOD=∠CBE，∠ADO=∠CEB，OA=BC，∴△AOD≌△CBE（AAS），∴OD=BE=1，∴OB=OE+BE=1；故答案为1．
考点：平行四边形的性质；坐标与图形性质．
10、1．
【解析】
试题分析：先根据平均数的定义确定平均数，再根据方差公式进行计算即可求出答案．
由平均数的公式得：（1+1+3+4+5）÷5=3，
∴方差=[（1﹣3）1+（1﹣3）1+（3﹣3）1+（4﹣3）1+（5﹣3）1]÷5=1．
考点：方差．
11、
【解析】
先根据两直线平行的问题得到k=2，然后把（1，3）代入y=2x+b中求出b即可．
【详解】
∵直线y=kx+b与y=2x+1平行，
∴k=2，
把(1,3)代入y=2x+b得2+b=3，解得b=1，
∴y=kx+b的表达式是y=2x+1.
故答案为：y=2x+1.
此题考查一次函数中的直线位置关系，解题关键在于求k的值.
12、
【解析】
先把（-1，0）代入y=kx+b得b=k，则k（x-3）+b＜0化为k（x-3）+k＜0，然后解关于x的不等式即可．
【详解】
解：把（-1，0）代入y=kx+b得-k+b=0，解b=k，
则k（x-3）+b＜0化为k（x-3）+k＜0，
而k＜0，
所以x-3+1＞0，
解得x＞1．
故答案为x＞1．
本题考查了一次函数与一元一次不等式：从函数的角度看，就是寻求使一次函数y=kx+b的值大于（或小于）0的自变量x的取值范围；从函数图象的角度看，就是确定直线y=kx+b在x轴上（或下）方部分所有的点的横坐标所构成的集合.
13、
【解析】
延长CH交FG的延长线于点N，由条件可以得出△CDH≌△NFH，就可以得出CH=NH，CD=NF，求出NG的长，根据勾股定理求出CN的长，从而可求出CH的长.
【详解】
解：延长CH交FG的延长线于点N，
∵FG∥CD,
∴∠CDH=∠NFH.
∵点为的中点，
∴DH=FH.
在△CDH和△NFH中，
∵∠CDH=∠NFH，
DH=FH，
∠CHD=∠NHF,
∴△CDH≌△NFH，
∴CH=NH，CD=NF=10，
∴NG=4,
∴CN=,
∴CH=2.
故答案为：2.
本题考查了矩形的性质的运用，菱形的性质的运用，全等三角形的判定及性质的运用，等腰直角三角形的性质的运用，特殊角的三角函数值的运用．解答时证明三角形全等是解答本题的关键．
三、解答题（本大题共5个小题，共48分）
14、解：（1）22.1．
（2）设需要售出x部汽车，
由题意可知，每部汽车的销售利润为：21－[27－0.1（x－1）]=（0.1x＋0.9）（万元），
当0≤x≤10，根据题意，得x·（0.1x＋0.9）＋0.3x=12，整理，得x2＋14x－120=0，
解这个方程，得x1=－20（不合题意，舍去），x2=2．
当x＞10时，根据题意，得x·（0.1x＋0.9）＋x=12，整理，得x2＋19x－120=0，
解这个方程，得x1=－24（不合题意，舍去），x2=3．
∵3＜10，∴x2=3舍去．
答：要卖出2部汽车．
【解析】
一元二次方程的应用．
（1）根据若当月仅售出1部汽车，则该部汽车的进价为27万元，每多售出1部，所有售出的汽车的进价均降低0.1万元/部，得出该公司当月售出3部汽车时，则每部汽车的进价为：27－0.1×2=22.1．，
（2）利用设需要售出x部汽车，由题意可知，每部汽车的销售利润，根据当0≤x≤10，以及当x＞10时，分别讨论得出即可．
15、（1）；（2）,
【解析】
（1）利用待定系数法求一次函数解析式即可；
（2）根据一次函数的平移规律：左加右减，上加下减，即可求出平移后的解析式，然后将y=0代入求出x的值，即可求出结论．
【详解】
解：（1）把点，代入中，得：

解得
∴一次函数的解析式为
（2）将该函数的图象向下平移3个单位后得．
当时，解得：
∴平移后函数图象与轴的交点坐标为
此题考查的是求一次函数的解析式和一次函数图象的平移，掌握用待定系数法求一次函数的解析和一次函数的平移规律：左加右减，上加下减是解决此题的关键．
16、（1）；；（2）证明见解析；(3)．
【解析】
（1）首先利用待定系数法求得反比例函数的解析式，然后求得B的坐标，则利用待定系数法即可求得直线的解析式；
（2）过点B作BD⊥OC于点D，在直角△OBD和直角△OBC中，利用勾股定理求得和，然后利用勾股定理的逆定理即可证明；
（3）分成Q在B的左侧和右侧两种情况讨论，当在右侧时一定不成立，当在左侧时，判断是否存在点Q时∠QCO=90°-α即可．
【详解】
(1)设反比例函数的解析式是y=kx，
把(1,8)代入得k=8，
则反比例函数表达式为，
把(m,2)代入得，
则B的坐标是(4,2).
根据题意得：，
解得：，
，则直线表达式y=−2x+10；
(2)过点B作BD⊥OC于点D,(图1)则D的坐标是(4,0).
在y=−2x+10中，令y=0，解得x=5，则OC=5.
∵在直角△OBD中，BD=2，DC=OC−OD=5−4=1，
则，
同理,直角△BCD中, ，
∴，
∴△OBC是直角三角形；
(3)当Q在B的右侧时一定不成立，
在y=−2x+10中,令x=0,则y=10,

则当Q在的左边时,(图2)tan∠ACO=tanα=2，
则tan(90°−α)= .
当∠QCO=90°−α时,Q的横坐标是p,则纵坐标是，
tan∠QCO=tan(90°−α)= :(5−p)=
即，
△=25−4×16=−39<0，则Q不存在，
故当Q在AB之间时，满足条件，
因而2此题考查反比例函数以及三角函数，解题关键在于结合反比例函数的图象解决问题.
17、（1）60 （2）61分
【解析】
（1）把各分数段的人数相加即可．
（2）用总分数除以总人数即可求出平均分．
【详解】
（1）（名）
故该班有60名学生．
（2）（分）
故这次测验的平均成绩为61分．
本题考查了条形统计图的问题，掌握条形统计图的性质、平均数的算法是解题的关键．
18、（1）109 ， 1.（2）109；（3）110.2
【解析】
（1）把6个数从小到大排列，按照中位数、众数的概念即可得出结论；
（2）把平时测试成绩相加，再求出其平均数即可；
（3）取4次月考成绩平均分的20％加上期中成绩的30﹪加上期末成绩的50﹪计算即可.
【详解】
解：（1）这6个数从小到大排列为：105，1，1，110，112，113，中位数是=109，众数是1．
故答案为：109，1；
（2）平时测试的数学平均成绩=（分）；
（3）总评成绩=（分）
答：该生本学期的数学总评成绩为110.2分。
本题考查了中位数和众数的定义，熟练的掌握数据的分析和加权平均数的计算方法是解题的关键.
一、填空题（本大题共5个小题，每小题4分，共20分）
19、x≥1
【解析】
试题分析：二次根式有意义的条件：二次根号下的数为非负数，二次根式才有意义.
由题意得，．
考点：二次根式有意义的条件
点评：本题属于基础应用题，只需学生熟练掌握二次根式有意义的条件，即可完成.
20、3或-1
【解析】
据题意得，∵（x+2）*5=（x+2）2-52∴x2+4x-21=0，∴（x-3）（x+1）=0，∴x=3或x=-1．
21、1
【解析】
试题分析：OP平分∠MON，PE⊥OM于E，PF⊥ON于F，
∴PE=PF，∠1=∠2，
在△AOP与△BOP中，
，
∴△AOP≌△BOP，
∴AP=BP，
在△EOP与△FOP中，
，
∴△EOP≌△FOP，
在Rt△AEP与Rt△BFP中，
，
∴Rt△AEP≌Rt△BFP，
∴图中有1对全等三角形，
故答案为1．
考点：角平分线的性质，全等三角形的判定和性质．
22、<
【解析】
方差用来计算每一个变量（观察值）与总体均数之间的差异，所以从图像看苗高的波动幅度，可以大致估计甲、乙两块地苗高数据的方差.
【详解】
解：由图可知，甲、乙两块地的苗高皆在12cm上下波动，但乙的波动幅度比甲大，
∴ 则
故答案为：<
本题考查了方差，方差反映了数据的波动程度，方差越大，数据的波动越大，正确理解方差的含义是解题的关键.
23、②③④
【解析】
分析：分别计算该组数据的平均数，众数，方差后找到正确的答案即可．
详解：∵﹣6，﹣3，x，2，﹣1，3的中位数是-1，∴分三种情况讨论：
①若x≤－3，则中位数是（－1－3）÷2=－2，矛盾；
②若x≥2，则中位数是（－1+2）÷2=0.5，矛盾；
③若-3＜x≤－1或－1≤x＜2，则中位数是（－1+x）÷2=－1，解得：x=﹣1；
平均数=（﹣6﹣3﹣1﹣1+2+3）÷6=﹣1．
∵数据﹣1出现两次，出现的次数最多，∴众数为﹣1；
方差=[（﹣6+1）2+（﹣3+1）2+（﹣1+1）2+（2+1）2+（﹣1+1）2+（3+1）2]=9，∴正确的序号是②③；
故答案为②③．
点睛：本题考查了方差、平均数、中位数及众数的知识，属于基础题，掌握各部分的定义及计算方法是解题的关键．
二、解答题（本大题共3个小题，共30分）
24、（1）＝；（2）见解析；（3）见解析
【解析】
（1）根据折叠的性质、平行四边形的性质、以及等腰三角形的判定与性质可猜想为相等；
（2）先证明∠EDF=∠EGF，再证明EG=ED，则等边对等角得：∠EGD=∠EDG，相减可得结论；
（3）分别表示BF、CF、BC的长，证明ABCD是矩形得：∠C=90°，在Rt△BCF中，由勾股定理列式可得结论．
【详解】
解：（1）GF=DF，
故答案为：=；
（2）理由是：
连接DG，
由折叠得：AE=EG，∠A=∠BGE，
∵E在AD的中点，
∴AE=ED，
∴ED=EG，
∴∠EGD=∠EDG，
∵四边形ABCD是平行四边形，
∴AB∥CD，
∴∠A+∠ADC=180°，
∵∠BGE+∠EGF=180°，
∴∠EDF=∠EGF，
∴∠EDF-∠EDG=∠EGF-∠EGD，
即∠GDF=∠DGF，
∴GF=DF；
（3）证明：如图2，由（2）得：DF=GF=b，
由图可得：BF=BG+GF=a+b，
由折叠可得：AB=BG=a，AE=EG=c，
在ABCD中，
BC=AD=2AE=2c，CD=AB=a，
∴CF=CD-DF=a-b，
∵∠A=90°，
∴ABCD是矩形，
∴∠C=90°，
在Rt△BCF中，由勾股定理得，
BC2+CF2=BF2，
∴(2c)2+(a-b)2=(a+b)2，
整理得：c2=ab．
本题考查了平行四边形的性质、矩形的性质和判定、勾股定理、折叠的性质、等腰三角形的性质与判定，难度适中，熟练掌握折叠前后的边和角相等是关键．
25、 (1)MN＝2+；(2)y＝•x•2x(0＜x＜4)；(3)1或1．
【解析】
（1）解直角三角形求出AD，利用梯形中位线定理即可解决问题；
（2）求出AD，利用梯形的面积公式计算即可；
（3）作AG⊥BC于G，EH⊥BC于H．想办法证明△ABC≌△ECB，推出AC=BE=4，因为AC⊥BE，可得S四边形ABCE=•AC•BE，由此计算即可；
【详解】
(1)∵AD∥BC，
∴∠DAC＝∠ACB＝30°，
在Rt△ACD中，∵AC＝4，∠D＝90°，∠ACD＝30°，
∴CD＝AC＝2，AD＝CD＝2，
∵AM＝BM，DN＝CN，
∴MN是梯形ABCD的中位线，
∴MN＝(AD+BC)＝2+．
(2)在Rt△ACD中，∵AC＝4，∠D＝90°，CD＝x，
∴AD＝＝，
∴y＝•(AD+BC)•CD＝(+4)x＝•x•+2x(0＜x＜4)．
(3)①当点E在线段AD上时，作AG⊥BC于G，EH⊥BC于H．
∵AD∥BC，AG⊥BC于G，EH⊥BC于H．
∴AG＝EH，∠AGB＝∠EHC＝90°，
∵AB＝EC，
∴Rt△ABG≌Rt△ECH，
∴∠ABC＝∠ECB，
∵AB＝EC，BC＝CB，
∴△ABC≌△ECB，
∴AC＝BE＝4，
∵AC⊥BE，
∴S四边形ABCE＝•AC•BE＝×4×4＝1．
②当点E在AD的延长线上时，易证四边形ABCE是平行四边形，
∵BE⊥AC，
∴四边形ABCE是菱形，
∵BC＝AC＝AB，
∴△ABC，△ACE是等边三角形，
∴S四边形ABCE＝2××42＝1．
本题考查四边形综合题、勾股定理、梯形的中位线定理、梯形的面积、全等三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考压轴题．
26、（1）原方程无解；（2）x≤1，数轴见解析；
【解析】
（1）利用解分式方程的一般步骤求解即可．
(2)求出两个不等式的解集，根据找不等式组解集的规律找出不等式组的解集即可．
【详解】
（1）去分母，方程两边同时乘以（x-3），可得： x-2=2（x-3）+1，
去括号可得：x-2=2x-6+1，
解得x=3，
检验：当x=3时，x-3=0，
∴x=3是分式方程的增根，原方程无解．
（2）解： ，
∵解不等式①得：x≤1，
解不等式②得：x＜4，
∴不等式组的解集为：x≤1，
在数轴上表示不等式组的解集为：
．
此题考查解分式方程，解一元一次不等式组，在数轴上表示不等式组的解集的应用，解此题的关键是能根据不等式的解集找出不等式组的解集．
题号
一
二
三
四
五
总分
得分
批阅人
成绩类别
第一次月考
第二次月考
期中
第三次月考
第四次月考
期末
成绩/分
105
110
108
113
108
112