辽宁省沈阳市翔宇中学2024-2025学年高三上学期10月月考数学试题

这是一份辽宁省沈阳市翔宇中学2024-2025学年高三上学期10月月考数学试题，共8页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

（试卷满分：150分考试时间：120分钟）
一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．
1．已知集合，集合，则（ ）
A．B．C．D．
2．已知命题；命题，则（ ）
A．和都是真命题B．和都是真命题
C．和都是真命题D．和都是真命题
3．已知，则（ ）
A．B．C．D．
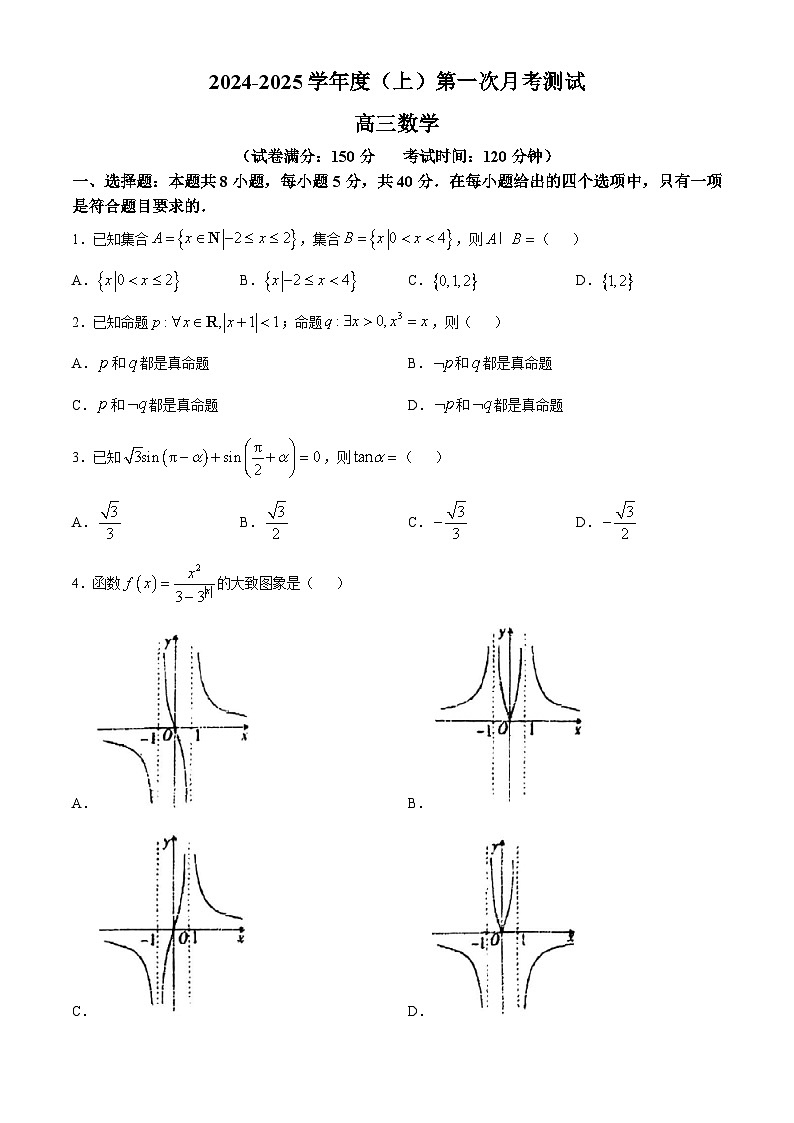
4．函数的大致图象是（ ）
A．B．
C．D．
5．已知函数，为了得到（为的导函数）的图象，则只需要将函数图象上的点（ ）
A．向左平移个单位长度，纵坐标缩短为原来的
B．向左平移个单位长度，纵坐标不变
C．向左平移个单位长度，纵坐标缩短为原来的
D．向左平移个单位长度，纵坐标不变
6．若函数在上单调递增，则实数的取值范围是（ ）
A．B．C．D．
7．已知，则（ ）
A．B．C．D．
8．中，角所对的边分别为，且边上的高为，则（ ）
A．的面积有最大值，且最大值为B．的面积有最大值，且最大值为
C．的面积有最小值，且最小值为D．的面积有最小值，且最小值为
二、选择题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目的要求全部选对的得6分，部分选对的得部分分，有选错的得0分。
9．已知函数为的导函数，则下列说法正确的是（ ）
A．B．为奇函数
C．的极小值为D．在上单调递增
10．已知函数，则下列结论正确的有（ ）
A．函数的最小正周期为
B．函数在上是增函数
C．若，则
D．若，则
11．已知定义域为的偶函数满足，当时，则（ ）
A．B．的图象关于点成中心对称
C．D．
三、填空题：本题共3小题，每小题5分，共15分．
12．已知，则______．
13．已知，且，则的最小值为______．
14．已知函数的图象关于直线对称，且在上单调，财正数的最大值为______．
四、解答题：本题共5小题，共77分．解答应写出文字说明、证明过程或演算步骤．
15．（13分）
已知中，角所对的边分别为，其中．
（1）求的值；
（2）若的面积为，周长为6，求的值．
16．（15分）
已知函数．
（1）当时，若在上单调递增，求实数的取值范围；
（2）若在处取得极值0，求的值．
17．（15分）
锐角中，角的对边分别为，且
（1）求的值；
（2）求的周长的取值范围．
18．（17分）
已知函数，曲线在点处切线的斜率为．
（1）比较与的大小；
（2）讨论的单调性；
（3）若有最小值，且最小值为，求的最大值．
19．（17分）
已知函数．
（1）将化成的形式；
（2）当时，求函数的递减区间；
（3）若在上的值域为，求的取值范围．
2024-2025学年度（上）第一次月考高三数学参考答案
1---8：DBCD BADC 9---11：BD ACD ABD
12--14：
15．（1）由正弦定理，已知可化为：，
因为，所以，即，
（不写扣1分）
因为，所以；（不写扣1分）
（2）由得：，
由得：，
所以，
解得：，
16．（1）时，，所以，
由题可知：在上恒成立，
即在上恒成立，即在上恒成立，
所以只需在上恒成立，即，
因为在上递减，所以，
所以；
（2）
由题，所以，解得：或，
当时，，函数在R上单调递增，无极值，不符合题意，舍去；
当时，，经检验，处取得极大值0，符合题意，所以．
17．（1）由正弦定理：，所以，
在中，，
所以；
所以
（2）由（1）及正弦定理得：，．
所以，
因为是锐角三角形且，
所以，则，
所以，
所以．
18．（1），由题：，
所以，即，
所以；
（2），
当时，在R上恒成立，所以在R上单调递增；
当时，的根为，
当时，递减，
当时，递增，
综上：当时，增区间为，无减区间；
当时，增区间为，减区间为
（3）由（2）知：当时，在R上单调递增，无最值；
当时，增区间为，减区间为，
所以．即，
，当时，，
当时，递增，
当时，递减，
所以当时，取得最大值，
所以
19．（1）；
（2）由（1），当时，，
由余弦函数图象可知，当，函数单调递减，
即时，函数单调递减，
所以时，的递减区间为；
（3）由题：函数的最小正周期为，对称轴为，
①若在上单调，则，
即时，，
因为
则，所以；
②若在上不单调，则在上的图象必定含一个最高点或最低点，且在上的图象无论经过任何一个最高点或任何一个最低点，的取值范围均相同；
假设在上的最高点为，则，
当，即时，，
此时取得最小值，的最小值为；
又，则，所以，
综上所述，