广西省梧州市名校2024-2025学年数学九年级第一学期开学教学质量检测试题【含答案】

这是一份广西省梧州市名校2024-2025学年数学九年级第一学期开学教学质量检测试题【含答案】，共22页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）一组数据4，5，7，7，8，6的中位数和众数分别是（ ）
A．7，7B．7，6.5C．6.5，7D．5.5，7
2、（4分）若等腰的周长是，一腰长为，底边长为，则与的函数关系式及自变量的取值范围是
A．B．
C．D．
3、（4分）若点P（-2，a）在第二象限，则a的值可以是（ ）
A．1B．-1C．0D．-2
4、（4分）下列式子：，，，，其中分式的数量有（ ）
A．1个B．2个C．3个D．4个
5、（4分）矩形与矩形如图放置，点共线，共线，连接，取的中点，连接，若，，则（ ）
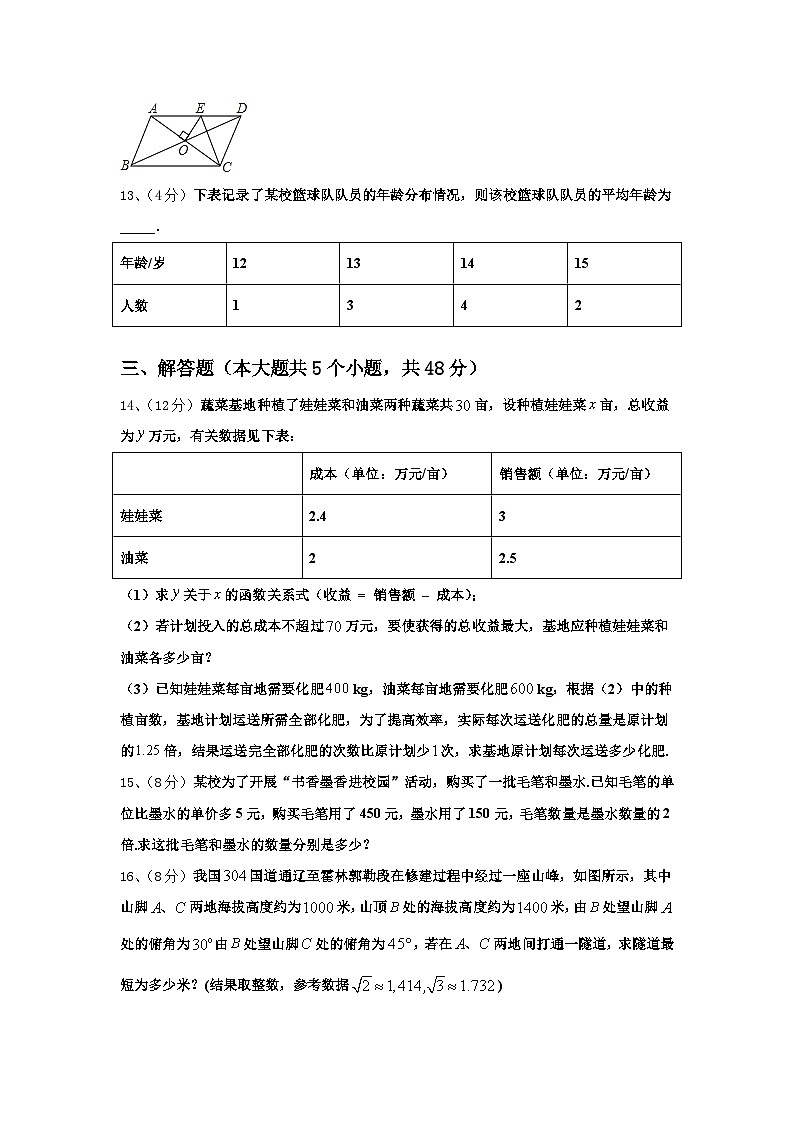
A．B．C．2D．
6、（4分）如果点在的图像上，那么在此图像上的点还有（ ）
A．（-3，2）B．（2，-3）C．（-2，-3）D．（0，0）
7、（4分）解不等式，解题依据错误的是（ ）
解：①去分母，得5（x+2）＜3（2x﹣1）
②去括号，得5x+10＜6x﹣3
③移项，得5x﹣6x＜﹣3﹣10
④合并同类项，得﹣x＜﹣13
⑤系数化1，得x＞13
A．②去括号法则B．③不等式的基本性质1
C．④合并同类项法则D．⑤不等式的基本性质2
8、（4分）某班抽取6名同学进行体育达标测试，成绩如下：80,90,75,80,75,80.下列关于对这组数据的描述错误的是（ ）
A．中位数是75B．平均数是80C．众数是80D．极差是15
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）如图，将正方形放在平面直角坐标系中，是坐标原点，点的坐标为，则点的坐标为__________.
10、（4分）已知a，b为一元二次方程x2+2x﹣9=0的两个根，那么a2+a﹣b的值为 ．
11、（4分）已知：，，代数式的值为_________.
12、（4分）如图，平行四边形 的周长为 , 相交于点 ， 交 于点 ，则 的周长为________ .
13、（4分）下表记录了某校篮球队队员的年龄分布情况，则该校篮球队队员的平均年龄为_____．
三、解答题（本大题共5个小题，共48分）
14、（12分）蔬菜基地种植了娃娃菜和油菜两种蔬菜共亩，设种植娃娃菜亩，总收益为万元，有关数据见下表：
（1）求关于的函数关系式（收益 = 销售额 – 成本）；
（2）若计划投入的总成本不超过万元，要使获得的总收益最大，基地应种植娃娃菜和油菜各多少亩？
（3）已知娃娃菜每亩地需要化肥kg，油菜每亩地需要化肥kg，根据（2）中的种植亩数，基地计划运送所需全部化肥，为了提高效率，实际每次运送化肥的总量是原计划的倍，结果运送完全部化肥的次数比原计划少次，求基地原计划每次运送多少化肥.
15、（8分）某校为了开展“书香墨香进校园”活动，购买了一批毛笔和墨水.已知毛笔的单位比墨水的单价多5元，购买毛笔用了450元，墨水用了150元，毛笔数量是墨水数量的2倍.求这批毛笔和墨水的数量分别是多少？
16、（8分）我国国道通辽至霍林郭勒段在修建过程中经过一座山峰，如图所示，其中山脚两地海拔高度约为米，山顶处的海拔高度约为米，由处望山脚处的俯角为由处望山脚处的俯角为，若在两地间打通一隧道，求隧道最短为多少米？(结果取整数，参考数据)
17、（10分）某中学八年级学生到离学校15千米的青少年营地举行庆祝十四岁生日活动，先遣队与大部队同时出发，已知先遣队的行进速度是大部队行进速度的1.2倍，预计先遣队比大部队早0.5小时到达目的地，求先遣队与大部队的行进速度。
18、（10分）（1）计算：
（2）已知：x＝+1，求x2﹣2x的值．
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）甲、乙两名射击手的100次测试的平均成绩都是9环，方差分别是S2甲＝0.8，S2乙＝0.35，则成绩比较稳定的是_____(填“甲”或“乙”)．
20、（4分）菱形ABCD的对角线cm，，则其面积等于______.
21、（4分）如图，正方形中，，点在边上，且.将沿对折至，延长交边于点，连接、.则下列结论：①：②；③：④.其中正确的有_（把你认为正确结论的序号都填上）
22、（4分）如图，在反比例函数与的图象上分别有一点，，连接交轴于点，若且，则__________．
23、（4分）如图，Rt△ABC中，∠ACB=90°，AB=6，D是AB的中点，则CD=_____．
二、解答题（本大题共3个小题，共30分）
24、（8分）计算
(1)()-()
(2)(2+3)(2-3)
25、（10分）在一次社会调查活动中，小华收集到某“健步走运动”团队中20名成员一天行走的步数，记录如下：
5640 6430 6520 6798 7325
8430 8215 7453 7446 6754
7638 6834 7326 6830 8648
8753 9450 9865 7290 7850
对这20个数据按组距1000进行分组，并统计整理，绘制了如下尚不完整的统计图表：
步数分组统计表
请根据以上信息解答下列问题：
（1）填空：m= ______ ，n= ______ ；
（2）补全频数发布直方图；
（3）这20名“健步走运动”团队成员一天行走步数的中位数落在______ 组；
（4）若该团队共有120人，请估计其中一天行走步数不少于7500步的人数．
26、（12分）如图，已知矩形ABCD中，点E是AB边上的一个动点，点F、G、H分别是CD、DE、CE的中点．
（1）求证：四边形EHFG是平行四边形；
（2）设AB＝4，AD＝3，求△EFG的面积．
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、C
【解析】
根据中位数与众数的概念和求解方法进行求解即可.
【详解】
将数据从小到大排列：4、5、6、7、7、8，
所以中位数为=6.5，众数是7，
故选C.
本题考查了中位数和众数，熟练掌握相关定义以及求解方法是解题的关键.①给定n个数据，按从小到大排序，如果n为奇数，位于中间的那个数就是中位数；如果n为偶数，位于中间两个数的平均数就是中位数．任何一组数据，都一定存在中位数的，但中位数不一定是这组数据里的数．②给定一组数据，出现次数最多的那个数，称为这组数据的众数．
2、C
【解析】
根据题意，等腰三角形的两腰长相等，即可列出关系式.
【详解】
依题意，，
根据三角形的三边关系得，
，得，
，得，
得，，
故与的函数关系式及自变量的取值范围是：，
故选．
本题考查了一次函数的应用，涉及了等腰三角形的性质，三角形的三边关系，做此类题型要注意利用三角形的三边关系要确定边长的取值范围．
3、A
【解析】
根据第二象限内点的纵坐标是正数判断.
【详解】
∵点P（-2，a）在第二象限，
∴a＞0，
∴1、0、-1、-2四个数中，a的值可以是1．
故选A．
本题考查了各象限内点的坐标的符号特征，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限（+，+）；第二象限（-，+）；第三象限（-，-）；第四象限（+，-）．
4、B
【解析】
根据分式定义：如果A，B表示两个整式，并且B中含有字母，那么式子叫做分式进行分析即可．
【详解】
解：，是分式，共2个，
故选：B．
此题主要考查了分式定义，关键是掌握分式的分母必须含有字母，而分子可以含字母，也可以不含字母，亦即从形式上看是的形式，从本质上看分母必须含有字母．
5、A
【解析】
如图，延长GH交AD于点M，先证明△AHM≌△FHG，从而可得AM=FG=1，HM=HG，进而得DM=AD-AM=2，继而根据勾股定理求出GM的长即可求得答案.
【详解】
如图，延长GH交AD于点M，
∵四边形ABCD、CEFG是矩形，
∴AD=BC=3，CG=EF=3，FG=CE=1，∠CGF=90°，∠ADC=90°，
∴DG=CG-CD=3-1=2，∠ADG=90°=∠CGF，
∴AD//FG，
∴∠HAM=∠HFG，∠AMH=∠FGH，
又AH=FH，
∴△AHM≌△FHG，
∴AM=FG=1，HM=HG，
∴DM=AD-AM=3-1=2，
∴GM=，
∵GM=HM+HG，
∴GH=，
故选A.
本题考查了矩形的性质，勾股定理，全等三角形的判定与性质，正确添加辅助线，熟练掌握相关知识是解题的关键.
6、C
【解析】
将代入即可求出k的值，再根据k＝xy解答即可．
【详解】
解：∵点在反比例函数的图象上，
∴k＝3×2＝1，
而只有C选项代入得：k＝−2×(-3)＝1．
故选：C．
本题考查了反比例函数图象上点的坐标特征，只要点在函数的图象上，就一定满足函数的解析式．反之，只要满足函数解析式就一定在函数的图象上．
7、D
【解析】
根据题目中的解答步骤可以写出各步的依据，从而可以解答本题．
【详解】
解：由题目中的解答步骤可知，
②去括号法则，故选项A正确，
③不等式的基本性质1，故选项B正确，
④合并同类项法则，故选项C正确，
⑤不等式的基本性质3，故选项D错误，
故选D．
本题考查解一元一次不等式，解答本题的关键是明确解一元一次不等式的方法．
8、A
【解析】
根据平均数，中位数，众数及极差的概念进行判断．
【详解】
解：将6名同学的成绩从小到大排列，第3、4个数都是80，故中位数是80，
∴答案A是错误的，其余选项均正确．
故选：A．
本题重点考查平均数，中位数，众数及极差的概念及其求法．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、
【解析】
过点E作EI⊥x轴于I，过点G作GH⊥x轴于H，根据同角的余角相等求出∠OEI=∠GOH，再利用“角角边”证明△EOI和△OGH全等，根据全等三角形对应边相等可得OH=EI，EI=OI，然后根据点G在第二象限写出坐标即可．
【详解】
解：过点E作EI⊥x轴于I，过点G作GH⊥x轴于H，如图所示：
∵四边形OEFG是正方形，
∴OE=OG，∠EOG =90°，
∴∠GOH+∠EOI=90°，
又∵∠OEI +∠EOI=90°，
∴∠OEI =∠GOH，
在△EOI和△OGH中，，
∴△EOI≌△OGH（AAS），
∴OH=EI=3，GH=OI=2，
∵点G在第二象限，
∴点G的坐标为（-3，2）．
故答案为（-3，2）．
本题考查了全等三角形的判定与性质，正方形的性质，坐标与图形性质，作辅助线构造出全等三角形是解题的关键.
10、1
【解析】
由根与系数的关系可得a+b=﹣2，a2+2a-9=0，继而将a2+a﹣b变形为a2+2a-(a+b)，然后将数值代入进行计算即可得.
【详解】
∵a，b为一元二次方程x2+2x﹣9=0的两根，
∴a+b=﹣2，a2+2a-9=0，
∴a2+2a =9，
∴a2+a﹣b=a2+2a﹣a-b=（a2+2a）-(a+b)=9+2=1，
故答案为1．
11、4
【解析】
根据完全平方公式计算即可求出答案．
【详解】
解：∵，，
∴x−y＝2，
∴原式＝（x−y）2＝4，
故答案为：4
本题考查二次根式的化简求值和完全平方公式，解题的关键是熟练运用完全平方公式，本题属于基础题型．
12、1
【解析】
根据平行四边形性质得出AD=BC，AB=CD，OA=OC，根据线段垂直平分线得出AE=CE，求出CD+DE+EC=AD+CD，代入求出即可．
【详解】
解：∵平行四边形ABCD，
∴AD=BC，AB=CD，OA=OC，
∵EO⊥AC，
∴AE=EC，
∵AB+BC+CD+AD=16，
∴AD+DC=1，
∴△DCE的周长是：CD+DE+CE=AE+DE+CD=AD+CD=1，
故答案为1．
本题考查了平行四边形性质、线段垂直平分线性质的应用，关键是求出AE=CE，主要培养学生运用性质进行推理的能力，题目较好，难度适中．
13、13.1．
【解析】
根据加权平均数的计算公式计算可得．
【详解】
解：该校篮球队队员的平均年龄为＝13.1
故答案为13.1．
本题主要考查加权平均数的计算方法，解题的关键是掌握平均数的定义和计算公式．
三、解答题（本大题共5个小题，共48分）
14、（1）；（2）基地应种植娃娃菜亩，种植油菜亩；（3）基地原计划每次运送化肥·
【解析】
（1）根据种植郁金香和玫瑰两种花卉共30亩，可得出种植玫瑰30-x亩，再根据“总收益=郁金香每亩收益×种植亩数+玫瑰每亩收益×种植亩数”即可得出y关于x的函数关系式；
（2）根据“投入成本=郁金香每亩成本×种植亩数+玫瑰每亩成本×种植亩数”以及总成本不超过70万元，可得出关于x的一元一次不等式，解不等式即可得出x的取值范围，再根据一次函数的性质即可解决最值问题；
（3）设原计划每次运送化肥mkg，实际每次运送1.25mkg，根据原计划运送次数比实际次数多1，可得出关于m的分式方程，解分式方程即可得出结论．
【详解】
解：（1）由题意得；
（2）由题意知，解得
对于，∵，∴随的增大而增大，
∴当时，所获总收益最大，此时.
答：基地应种植娃娃菜亩，种植油菜亩；
（3）设原计划每次运送化肥，实际每次运送 ，
需要运送的化肥总量是，
由题意可得
解得.
经检验，是原分式方程的解．
答：基地原计划每次运送化肥·
考查了一次函数的应用、解一元一次不等式以及分式方程的应用，解题的关键是：（1）根据数量关系找出y关于x的函数关系式；（2）根据一次函数的性质解决最值问题；（3）根据数量关系得出分式方程．本题属于基础题，难度不大，解决该题型题目时，根据数量关系列出方程（方程组或函数关系式）是关键．
15、墨水的单价是10元，则毛笔的单价是15元．
【解析】
设墨水的单价是x元，则毛笔的单价是（x+5）元，根据用450元购进的毛笔的数量是用150元购进的墨水的数量的2倍建立方程求出其解即可．
【详解】
设墨水的单价是x元，则毛笔的单价是（x+5）元，由题意，得
，
解得：x=10，
经检验，x=10是原方程的根
∴x+5=15元，
答：墨水的单价是10元，则毛笔的单价是15元．
本题考查分式方程的应用，分析题意，找到合适的等量关系是解决问题的关键．
16、1093
【解析】
作BD⊥AC于D，利用直角三角形的性质和三角函数解答即可．
【详解】
解：如图，作BD⊥AC于D，
由题意可得：BD＝1400﹣1000＝400（米），
∠BAC＝30°，∠BCA＝45°，
在Rt△ABD中，
∵，即，
∴AD＝400（米），
在Rt△BCD中，
∵，即，
∴CD＝400（米），
∴AC＝AD+CD＝400+400≈1092.8≈1093（米），
答：隧道最短为1093米．
本题考查解直角三角形、三角函数、特殊角的三角函数值等知识，解题的关键是添加辅助线构造直角三角形，学会用转化的思想解决问题，把问题转化为方程解决，属于中考常考题型．
17、大部队的行进速度为5千米/时,先遣队的行进速度为6千米/时
【解析】
【分析】设大部队的行进速度为x千米/时,则先遣队的行进速度为1.2x千米/时.由“先遣队比大部队早0.5小时到达目的地”，即时间关系可以列出，求解可得.
【详解】设大部队的行进速度为x千米/时,则先遣队的行进速度为1.2x千米/时.根据题意,可列出方程
.
解得 .
经检验, 是原方程的根,且符合题意.
当 时,
答:大部队的行进速度为5千米/时,先遣队的行进速度为6千米/时
【点睛】本题考核知识点：列分式方程解应用题.解题关键点：根据时间差关系列出方程.
18、（1）；（2）1.
【解析】
（1）根据二次根式的乘除法和加减法可以解答本题；
（2）根据x的值和平方差公式可以解答本题．
【详解】
（1）
＝
＝
＝2；
（2）∵x＝+1，
∴x2﹣2x
＝x（x﹣2）
＝
＝
＝5﹣1
＝1．
本题考查二次根式的化简求值，解答本题的关键是明确二次根式化简求值的方法．
一、填空题（本大题共5个小题，每小题4分，共20分）
19、乙
【解析】
根据方差的定义，方差越小数据越稳定，即可得出答案．
【详解】
解：∵甲、乙的平均成绩都是9环，方差分别是S甲2＝0.8，S乙2＝0.35，
∴S甲2＞S乙2，
∴成绩比较稳定的是乙；
故答案为：乙．
本题考查了方差的意义．方差是用来衡量一组数据波动大小的量，方差越大，表明这组数据偏离平均数越大，即波动越大，数据越不稳定；反之，方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定．
20、
【解析】
根据菱形的性质，菱形的面积等于两条对角线乘积的一半，代入数值计算即可。
【详解】
解：菱形ABCD的面积=
=
=
本题考查了菱形的性质：菱形的面积等于两条对角线乘积的一半。
21、①②③④
【解析】
根据翻折变换的性质和正方形的性质可证△ABG≌△AFG；由①和翻折的性质得出△ABG≌△AFG，△ADE≌△AFE，即可得出；在直角△ECG中，根据勾股定理可证BG=GC；通过证明∠AGB=∠AGF=∠GFC=∠GCF，由平行线的判定可得AG∥CF.
【详解】
解：①正确，∵四边形ABCD是正方形，将△ADE沿AE对折至△AFE，
∴AB=AD=AF，
在△ABG与△AFG中，;
△ABG≌△AFG（SAS）；
②正确，
∵由①得△ABG≌△AFG，
又∵折叠的性质，△ADE≌△AFE，
∴∠BAG =∠FAG，∠DAE=∠EAF，
∴∠EAG=∠FAG+∠EAF=90°×=45°；
③正确，
∵EF=DE=CD=2，
设BG=FG=x，则CG=6-x，
在直角△ECG中，
根据勾股定理，得（6-x）2+42=（x+2）2，
解得x=3，
∴BG=3=6-3=GC；
④正确，
∵CG=BG=GF，
∴△FGC是等腰三角形，∠GFC=∠GCF，
又∠AGB=∠AGF，∠AGB+∠AGF=180°-∠FGC=∠GFC+∠GCF，
∴∠AGB=∠AGF=∠GFC=∠GCF，
∴AG∥CF；
本题考查了翻折变换的性质和正方形的性质，全等三角形的判定与性质，勾股定理，平行线的判定，此题综合性较强，难度较大，解题的关键是注意数形结合思想应用.
22、
【解析】
过点E作EM⊥x轴于点M，过点F作FN⊥x轴于点N，根据平行线分线段成比例定理得：NO=2MO=2，从而可得F（2，2），结合E（-1，1）可得直线EF的解析式，求出点G的坐标后即可求解．
【详解】
过点E作EM⊥x轴于点M，过点F作FN⊥x轴于点N，如图：
∴EM∥GO∥FN
∵2EG=FG
∴根据平行线分线段成比例定理得：NO=2MO
∵E（-1，1）
∴MO=1
∴NO=2
∴点F的横坐标为2
∵F在的图象上
∴F（2，2）
又∵E（-1，1）
∴由待定系数法可得：直线EF的解析式为：y=
当x=0时，y=
∴G（0，）
∴OG=
故答案为：.
此题考查反比例函数的综合应用，平行线分线段成比例定理，待定系数法求一次函数的解析式，解题关键在于掌握待定系数法求解析式.
23、1
【解析】
根据直角三角形斜边上的中线等于斜边的一半解答．
【详解】
∵∠ACB=90°，D为AB的中点，
∴CD=AB=×6=1．
故答案为1．
本题考查了直角三角形斜边上的中线等于斜边的一半的性质，熟记性质是解题的关键．
二、解答题（本大题共3个小题，共30分）
24、 (1) ；(2)-1．
【解析】
（1）先把二次根式化为最简二次根式，然后合并即可；
（2）利用平方差公式计算．
【详解】
(1)原式=
=；
(2)原式=8-9=-1．
本题考查了二次根式的混合运算：先把二次根式化为最简二次根式，然后进行二次根式的乘除运算，再合并即可．在二次根式的混合运算中，如能结合题目特点，灵活运用二次根式的性质，选择恰当的解题途径，往往能事半功倍．
25、（1）4；1；（2）见解析；（3）B；（4）48.
【解析】
（1）根据题目中的数据即可直接确定m和n的值；
（2）根据（1）的结果即可直接补全直方图；
（3）根据中位数的定义直接求解；
（4）利用总人数乘以对应的比例即可求解．
【详解】
解：（1）由记录的数据可知，7500≤x＜8500的有8430、8215、7638、7850这4个，即m=4；
9500≤x＜10500的有9865这1个，即n=1．
故答案为4；1；
（2）如图：
（3）由于一共20个数据，其中位数是第10、11个数据的平均数，
而第10、11个数据的平均数均落在B组，
∴这20名“健步走运动”团队成员一天行走步数的中位数落在B组；
故答案为B；
（4）120×=48（人），
答：估计其中一天行走步数不少于7500步的有48人．
故答案为48.
本题考查读频数分布直方图的能力和利用统计图获取信息的能力．利用统计图获取信息时，必须认真观察、分析、研究统计图，才能作出正确的判断和解决问题．
26、（1）见解析；（2）S△FEG＝.
【解析】
（1）根据三角形的中位线定理求出FH∥DE，FG∥CE，根据平行四边形的判定求出即可；
（2）根据中线分三角形的面积为相等的两部分求解即可．
【详解】
（1）证明：因为点F、G、H分别是CD、DE、CE的中点，
所以，FH∥GE，FG∥EH，
所以，四边形EHFG是平行四边形；
（2）因为F为CD的中点，
所以DF=CD=AB=2，
因为G为DE的中点，所以，S△FDG＝S△FEG，
所以，S△FEG＝S△EFD＝．
本题考查了矩形的性质，三角形的面积，平行四边形的判定等知识点，能正确运用等底等高的三角形的面积相等进行计算是解此题的关键．
题号
一
二
三
四
五
总分
得分
年龄/岁
12
13
14
15
人数
1
3
4
2
成本（单位：万元/亩）
销售额（单位：万元/亩）
娃娃菜
2.4
3
油菜
2
2.5
组别
步数分组
频数
A
5500≤x＜6500
2
B
6500≤x＜7500
10
C
7500≤x＜8500
m
D
8500≤x＜9500
3
E
9500≤x＜10500
n