2024-2025学年云南省昭通一中高二（上）入学数学试卷（含答案）

这是一份2024-2025学年云南省昭通一中高二（上）入学数学试卷（含答案），共8页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。

1.函数f(x)= x−2⋅ x+5的定义域是( )
A. [2,+∞)B. [−5,+∞)
C. [−5,2]D. (−∞,−5]∪[2,+∞)
2.一元二次不等式2x2−x−1<0的解集是( )
A. (−∞,−12)∪(1,+∞)B. (−1,12)
C. (−∞,−1)∪(12,+∞)D. (−12,1)
3.i是虚数单位，复数2−i1+2i=( )
A. −1B. 1C. −iD. i
4.若sinθ=−2csθ，则sinθ(sinθ+csθ)=( )
A. −65B. −25C. 25D. 65
5.在△ABC中，已知B=120°，AC= 19，AB=2，则BC=( )
A. 1B. 2C. 5D. 3
6.如图，平行六面体各棱长为1，且∠A1AB=∠A1AD=∠BAD=60°，动点P在该几何体内部，且满足AP=xAB+yAD+(1−x−y)AA1(x,y∈R)，则|AP|的最小值为( )
A. 64B. 63C. 62D. 12
7.已知定义在R上的函数f(x)为偶函数，且f(x)在区间(−∞,0]上是增函数，记a=f(lg512),b=f(lg1215),c=f((12)15)，则a，b，c的大小关系是( )
A. a8.辅助角公式是我国清代数学家李普兰发现的用来化简三角函数的一个公式，其内容为asinx+bcsx= a2+b2sin(x+φ).已知函数f(x)=asinx+bcsx(其中a≠0，b∈R，tanφ=ba).若∀x∈R，f(x)≤f(π6)，则下列结论正确的是( )
A. f(π2)>f(π4)
B. f(x)的图象关于直线x=2π3对称
C. f(x)在[π6,7π6]上单调递增
D. 过点(a,b)的直线与f(x)的图象一定有公共点
二、多选题：本题共3小题，共18分。在每小题给出的选项中，有多项符合题目要求。
9.已知集合U={2,3,5,7,11,13,17}，A={2,5,7,13}，B={3,7,13,17}，C={7,13}，则下列关系正确的是( )
A. (∁UA)∩(∁UB)=∁U(A∪B)B. ∁U(∁UA)=∁U(∁UB)
C. A∩C=C∩BD. ∁U(A∩B)=∁UC
10.在正方体ABCD−A1B1C1D1中，E，F，G分别为BC，CC1，BB1的中点，则下列结论中正确的是( )
A. D1D⊥AF
B. A1G//平面AEF
C. 异面直线A1G与EF所成角的余弦值为 55
D. 点G到平面AEF的距离是点C到平面AEF的距离的2倍
11.已知函数f(x)=(sinx+cs|x|)|sinx−csx|，则下列说法正确的是( )
A. f(x)是周期函数
B. 若|f(x1)|+|f(x2)|=2，则x1+x2=kπ2(k∈Z)
C. f(x)在区间[−π2,π2]上是增函数
D. 函数g(x)=f(x)+1在区间[0,2π]上至少有2个零点
三、填空题：本题共3小题，每小题5分，共15分。
12.某班男女生的比例为3：2，全班的平均身高为168cm，若女生的平均身高为159cm，则男生的平均身高为______cm．
13.已知函数f(x)=x2+2x+2−x，若不等式f(1−ax)14.2023年10月26日神舟十七号载人飞船在长征二号F遥十七运载火箭的托举下点火升空，成功进入预定轨道.我国在航天领域取得的巨大成就，得益于我国先进的运载火箭技术.根据火箭理想速度公式v=v0⋅lnMm，可以计算理想状态下火箭的最大速度v(m/s)，其中v0(m/s)是喷流相对速度，m(kg)是火箭(除推进剂外)的质量，M(kg)是推进剂与火箭质量的总和，Mm称为总质比.已知甲型火箭喷流相对速度为2000m/s．
(i)当总质比为9时，甲型火箭的最大速度为______m/s；
(ii)若经过材料更新和技术改进后，甲型火箭的喷流相对速度提高到原来的32倍，总质比变为原来的12.若要使火箭的最大速度至少增加1000m/s，则在材料更新和技术改进前总质比的最小值为______．
(所有结果保留整数，参考数据：ln3≈1.1，2.718四、解答题：本题共5小题，共77分。解答应写出文字说明，证明过程或演算步骤。
15.(本小题13分)
已知函数f(2x−1)=16x2−2x．
(1)求函数f(x)的解析式；
(2)求函数y=lgaf(x)的单调增区间．
16.(本小题15分)
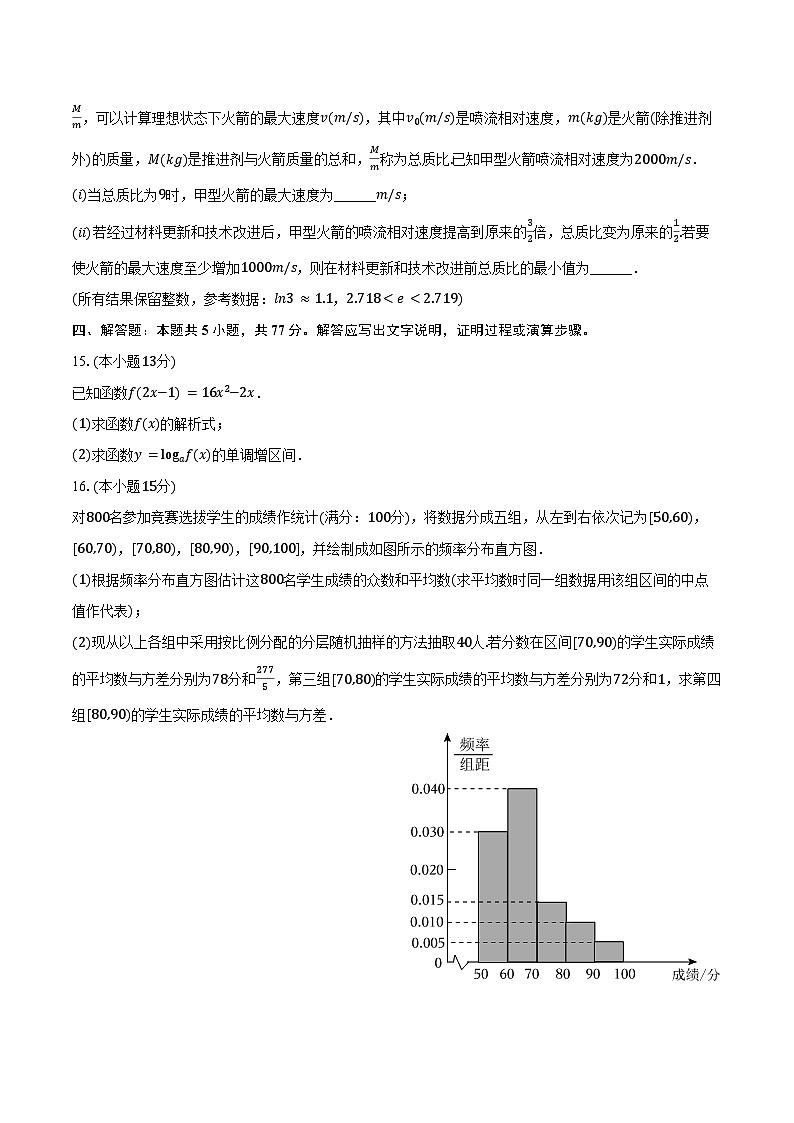
对800名参加竞赛选拔学生的成绩作统计(满分：100分)，将数据分成五组，从左到右依次记为[50,60)，[60,70)，[70,80)，[80,90)，[90,100]，并绘制成如图所示的频率分布直方图．
(1)根据频率分布直方图估计这800名学生成绩的众数和平均数(求平均数时同一组数据用该组区间的中点值作代表)；
(2)现从以上各组中采用按比例分配的分层随机抽样的方法抽取40人.若分数在区间[70,90)的学生实际成绩的平均数与方差分别为78分和2775，第三组[70,80)的学生实际成绩的平均数与方差分别为72分和1，求第四组[80,90)的学生实际成绩的平均数与方差．
17.(本小题15分)
在一场娱乐晚会上，有5位民间歌手(1至5号)登台演唱，由现场数百名观众投票选出最受欢迎歌手.各位观众需彼此独立地在选票上选3名歌手，其中观众甲是1号歌手的歌迷，他必选1号，不选2号，另在3至5号中随机选2名，观众乙和丙对5位歌手的演唱没有偏爱，因此在1至5号中随机选3名歌手．
(1)求观众甲选中3号歌手且观众乙未选中3号歌手的概率；
(2)X表示3号歌手得到观众甲、乙、丙的票数之和，求X=2的概率．
18.(本小题17分)
如图，矩形ABCD中，AB=3，BC=4.E，F分别在线段BC和AD上，EF//AB，将矩形ABEF沿EF折起．记折起后的矩形为MNEF，且平面MNEF⊥平面ECDF．
(Ⅰ)求证：NC//平面MFD；
(Ⅱ)若EC=3，求证：ND⊥FC；
(Ⅲ)求四面体NFEC体积的最大值．
19.(本小题17分)
在锐角△ABC中，角A，B，C的对边分别为a，b，c，且a2(1−sin2B)+b2(1−sin2A)=c2．
(1)求角C；
(2)若a=2，求△ABC的面积S的取值范围．
参考答案
1.A
2.D
3.C
4.C
5.D
6.B
7.C
8.D
9.ACD
10.BD
11.ABD
12.174
13.(−2,2)
14.4400 22
15.解：(1)f(2x−1)=16x2−2x=4(2x−1)2+14x−4=4(2x−1)2+7(2x−1)+3，
所以f(x)=4x2+7x+3．
(2)f(x)=4x2+7x+3=(4x+3)(x+1)，
所以f(x)是对称轴为x=−78，开口向上的二次函数，
且f(x)>0的解集为(−∞,−1)∪(−34,+∞)，
故f(x)在(−∞,−1)上单调递减，在(−34,+∞)单调递增．
当a>1时，函数y=lgax是增函数，
故函数y=lgaf(x)在(−∞,−1)上单调递减，在(−34,+∞)单调递增；
当0函数y=lgax是减函数，函数y=lgaf(x)在(−∞,−1)上单调递增，在(−34,+∞)单调递减；
16.解：(1)根据频率分布直方图估计这800名学生成绩的众数为60+702=65(分)；
平均数约为55×0.3+65×0.4+75×0.15+85×0.1+95×0.05=67(分)；
(2)∵第三组与第四组的频率之比为3：2，
设第四组[80,90)的学生实际成绩的平均数与方差分别为x，y，
∴根据题意可得78=35×72+25x，解得x=87，
∴2775=35[1+(72−78)2]+25[y+(87−78)2]，
解得y=2，
∴第四组[80,90)的学生实际成绩的平均数为87(分)，方差为2．
17.解：(1)设事件A表示“观众甲选中3号歌手且观众乙未选中3号歌手”，
观众甲选中3号歌手的概率为23，
观众乙未选中3号歌手的概率为1−35=25，
所以P(A)=23×25=415；
(2)用事件B，C，D分别表示“甲、乙、丙选中3号歌手”，
根据题意P(B)=23，P(C)=35，P(D)=35，
X=2意味着甲、乙、丙三人中只有2人选中3号歌手，
所以P(X=2)=P(BCD−)+P(BC−D)+P(B−CD)=23×35×25+23×25×35+13×35×35=1125．
18.(Ⅰ)证明：因为四边形MNEF，EFDC都是矩形，
所以MN//EF//CD，MN=EF=CD，
所以四边形MNCD是平行四边形，
所以NC//MD，
因为NC⊄平面MFD，MD⊂平面MFD，
所以NC//平面MFD.
(Ⅱ)证明：连接ED，设ED∩FC=O，
因为平面MNEF⊥平面ECDF，平面MNEF∩平面ECDF=EF，且NE⊥EF，NE⊂平面NEFM，
所以NE⊥平面ECDF，
又因为FC⊂平面ECDF，
所以FC⊥NE，
又矩形ECDF中，EC=CD，
所以矩形ECDF为正方形，
所以 FC⊥ED，
又因为FC⊥NE，NE∩ED=E，NE⊂平面NED，ED⊂平面NED，
所以FC⊥平面NED，
又因为ND⊂平面NED，
所以ND⊥FC.
(Ⅲ)解：设NE=x，则EC=4−x，其中0由(Ⅰ)得NE⊥平面FEC，
所以四面体NFEC的体积为：
VN−FEC=13S△EFC⋅NE=12x(4−x)，
所以VN−FEC≤12[x+(4−x)2]2=2，
当且仅当x=2时，等号成立，
故求四面体NFEC体积的最大值为2.
19.解：(1)由a2(1−sin2B)+b2(1−sin2A)=c2，得a2+b2−c2=a2sin2B+b2sin2A，
由余弦定理得2abcsC=a2sin2B+b2sin2A，
再由正弦定理及倍角公式得2csC=absin2B+basin2A=sinAsinB⋅sin2B+sinBsinA⋅sin2A
=2sinAcsB+2sinBcsA=2sin(A+B)=2sinC，
得csC=sinC，即tanC=1，
故在锐角△ABC中有C=π4；
(2)a=2，C=π4，则S=12absinC= 22b，
由正弦定理asinA=bsinB，有b=asinBsinA=2sin(3π4−A)sinA，
所以b=2sin(3π4−A)sinA= 2sinA+ 2csAsinA= 2+ 2csAsinA，
又△ABC是锐角三角形，有0得A∈(π4,π2)，则tanA∈(1,+∞)，
所以S= 22b=1+csAsinA=1+1tanA∈(1,2)，
即△ABC的面积S的取值范围为(1,2)．