湘教版（2024）八年级下册2.7 正方形习题ppt课件

这是一份湘教版（2024）八年级下册2.7 正方形习题ppt课件，共37页。PPT课件主要包含了名师点金，∴AF∥GH，∴AG＝GH，故选A，①②③④，1求α的值等内容，欢迎下载使用。

正方形的判定方法：要判定一个四边形是正方形，最常用的方法就是先证明它是菱形(或矩形)，再证明这个菱形(或矩形)有一个角是直角(或有一组邻边相等)，其实质就是根据正方形的定义来判定.当然也可以先证四边形是平行四边形，再证有一组邻边相等且有一个角是直角，或证这个平行四边形的对角线相等并且互相垂直.
知识点1　在菱形或矩形的基础上判定正方形1.在菱形ABCD中，若要添加一个条件后，使它是正方形，则添加的条件可以是(　　)
在菱形ABCD中，AB⊥BC，可根据有一个角是直角的菱形是正方形得菱形ABCD是正方形；而添加AB＝AD或AC⊥BD或AC平分∠BAD都不能判定菱形ABCD是正方形.
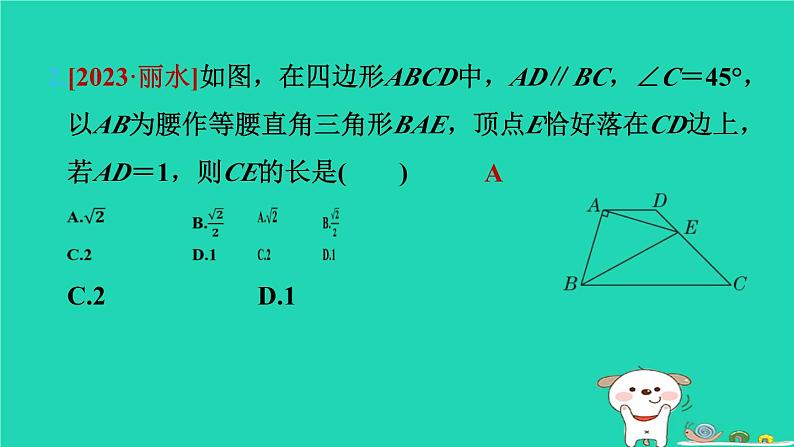
2.[2023·丽水]如图，在四边形ABCD中，AD∥BC，∠C＝45°，以AB为腰作等腰直角三角形BAE，顶点E恰好落在CD边上，若AD＝1，则CE的长是(　　)
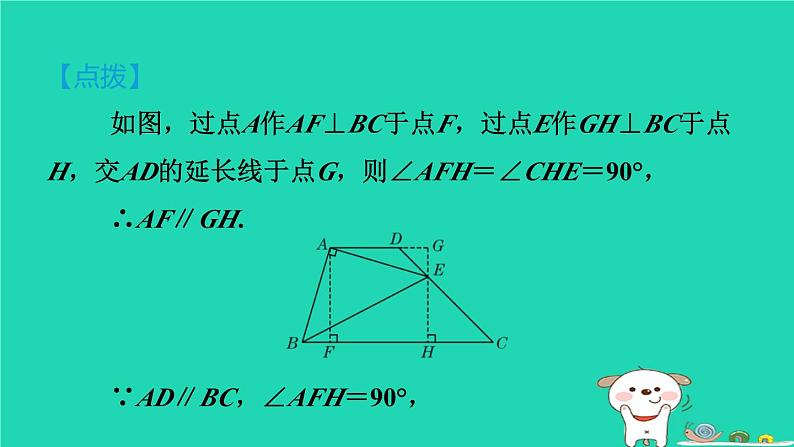
如图，过点A作AF⊥BC于点F，过点E作GH⊥BC于点H，交AD的延长线于点G，则∠AFH＝∠CHE＝90°，
∵AD∥BC，∠AFH＝90°，
∴四边形AFHG是矩形，
∴∠G＝∠FAG＝90°.
∵△ABE是等腰直角三角形，
∴AB＝AE，∠BAE＝90°，
∴∠FAG＝∠BAE＝90°，∴∠BAF＝∠EAG，
易知∠AFB＝∠G＝90°，
∴△AFB≌△AGE(AAS).
∴AF＝AG，∴矩形AFHG是正方形.
∵AG∥BC，∴∠C＝∠EDG＝45°.
∴△CHE和△DGE是等腰直角三角形.
∴DG＝EG，CH＝EH，
∴AD＝EH＝1.∴CH＝1.
知识点2　在四边形或平行四边形的基础上判定正方形3. [2023·绍兴 新视角·动点探究题]如图，在平行四边形ABCD中，AD＝2AB＝2，∠ABC＝60°，点E，F是对角线BD上的动点，且BE＝DF，点M，N分别是边AD，边BC上的动点.下列4种说法：
①存在无数个平行四边形MENF；②存在无数个矩形MENF；③存在无数个菱形MENF；④存在无数个正方形MENF.其中正确的有(　　)
连接AC，MN，AC交BD于点O.∵四边形ABCD是平行四边形，∴OA＝OC，OB＝OD.∵BE＝DF，∴OE＝OF.当MN过点O时，易证OM＝ON，∴四边形MENF为平行四边形.∵点E，F，M，N是动点，∴存在无数个平行四边形MENF；当MN过点O，MN＝EF时，四边形MENF是矩形，∵点E，F，M，N是动点，∴存在无数个矩形MENF；
当MN过点O，MN⊥EF时，四边形MENF是菱形，∵点E，F是动点，∴存在无数个菱形MENF；当MN过点O，MN＝EF且MN⊥EF时，四边形MENF是正方形，符合要求的正方形只有一个，故①②③正确，④错误.
4.[2022·攀枝花]如图，以△ABC的三边为边在BC上方分别作等边三角形ACD、等边三角形ABE、等边三角形BCF，且点A在△BCF内部，给出以下结论：
①四边形ADFE是平行四边形；②当∠BAC＝150°时，四边形ADFE是矩形；③当AB＝AC时，四边形ADFE是菱形；④当AB＝AC，且∠BAC＝150°时，四边形ADFE是正方形.其中正确结论有 　①②③④　⁠(填序号).
①利用SAS证明△EFB≌△ACB，得出EF＝AC＝AD；同理由△CDF≌△CAB，得DF＝AB＝AE；根据两组对边分别相等的四边形是平行四边形得出四边形ADFE是平行四边形，即可判断结论①正确；
②当∠BAC＝150°时，求出∠EAD＝90°，根据有一个角是90°的平行四边形是矩形即可判断结论②正确；
③先证明AE＝AD，再根据一组邻边相等的平行四边形是菱形即可判断结论③正确；
④根据正方形的判定：既是菱形，又是矩形的四边形是正方形即可判断结论④正确.
知识点3　中点四边形5.如图，点E，F，G，H分别是四边形ABCD的边AB，BC，CD，DA的中点，则下列说法中正确的个数是(　　)
①若AC＝BD，则四边形EFGH为矩形；②若AC⊥BD，则四边形EFGH为菱形；③若四边形EFGH是平行四边形，则AC与BD互相平分；④若四边形EFGH是正方形，则AC与BD互相垂直且相等.
【点拨】中点四边形的形状取决于原四边形两条对角线的 两条对角线相等→中点四边形是菱形.
中点四边形的形状取决于原四边形两条对角线的 　位置关
系　⁠和 　数量关系　⁠.两条对角线垂直→中点四边形是矩形，
两条对角线相等→中点四边形是菱形.
6.如图，AC，BD是四边形ABCD的对角线，点E，F分别是AD，BC的中点，点M，N分别是AC，BD的中点，连接EM，MF，FN，NE，要使四边形EMFN为正方形，则需添加的条件是(　　)
易错点　混淆特殊四边形的判定导致出错7.如图，一个四边形顺次添加下列条件中的三个条件便得到正方形：a.两组对边分别相等b.一组对边平行且相等c.一组邻边相等d.一个角是直角顺次添加的条件：①a→c→d；②b→d→c；③a→b→c，则正确的是(　　)
①由a得到两组对边分别相等的四边形是平行四边形，添加c得到一组邻边相等的平行四边形是菱形，再添加d得到有一个角是直角的菱形是正方形，故①正确；②由b得到一组对边平行且相等的四边形是平行四边形，添加d得到有一个角是直角的平行四边形是矩形，再添加c得到一组邻边相等的矩形是正方形，故②正确；
③由a得到两组对边分别相等的四边形是平行四边形，添加b得到一组对边平行且相等的平行四边形仍是平行四边形，再添加c得到一组邻边相等的平行四边形是菱形，不能得到四边形是正方形，故③不正确.
(2)请说明当▱ABCD的对角线满足什么条件时，四边形BPCO是正方形？
利用矩形为基础判定正方形
9. [2023·德阳 新考法·旋转法]将一副直角三角板DOE与AOC叠放在一起，如图①，∠O＝90°，∠A＝30°，∠E＝45°，OD＞OC.在两个三角板所在平面内，将三角板DOE绕点O顺时针方向旋转α(0°＜α＜90°)角到三角形D1OE1位置，使OD1∥AC，如图②.
【解】∵OD1∥AC，∴∠A＝∠AOD1＝30°，∵将三角板DOE绕点O顺时针方向旋转α(0°＜α＜90°)角到三角形D1OE1位置，∴∠AOD1＝α＝30°；
(2)如图③，继续将三角板DOE绕点O顺时针方向旋转，使点E落在AC边上点E2处，点D落在点D2处，设E2D2交OD1于点G，OE1交AC于点H，若点G是E2D2的中点，试判断四边形OHE2G的形状，并说明理由.
【解】四边形OHE2G是正方形，理由如下：∵∠E2OD2＝90°，OD2＝OE2，点G是E2D2的中点，∴E2G＝OG，E2G⊥OG.∴∠OGE2＝90°.∵OD1∥AC，∴∠CE2G＝90°.又∵∠E1OD1＝90°，∴四边形OHE2G是矩形，又∵E2G＝OG，∴四边形OHE2G是正方形.
利用正方形的性质与判定探究最值问题10. [新考法 逆向思维法]已知，四边形ABCD是正方形，△DEF绕点D旋转(DE＜AB)，∠EDF＝90°，DE＝DF，连接AE，CF.(1)如图①，求证：△ADE≌△CDF.
(2)直线AE与CF相交于点G.
Ⅰ.如图②，BM⊥AG于点M，BN⊥CF于点N，求证：四边形BMGN是正方形；
Ⅰ.【证明】如图②，设AG与CD相交于点P.
∵∠ADP＝90°，∴∠DAP＋∠DPA＝90°，
∵△ADE≌△CDF，∴∠DAE＝∠DCF.
∵∠DPA＝∠GPC，
∴∠DAE＋∠DPA＝∠GPC＋∠GCP＝90°，
∴∠PGN＝90°.∵BM⊥AG，BN⊥GN，
∴四边形BMGN是矩形，∴∠MBN＝90°.
∵四边形ABCD是正方形，
∴AB＝BC，∠ABC＝90°＝∠MBN，∴∠ABM＝∠CBN.
又∵∠AMB＝∠BNC＝90°，∴△AMB≌△CNB，
∴MB＝NB，∴矩形BMGN是正方形.
Ⅱ.如图③，连接BG，若AB＝4，DE＝2，直接写出在△DEF旋转的过程中，线段BG长度的最小值.