广东省广州番禺区七校联考2024年九年级数学第一学期开学检测试题【含答案】

这是一份广东省广州番禺区七校联考2024年九年级数学第一学期开学检测试题【含答案】，共22页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）已知正比例函数的图象上两点、，且，下列说法正确的是
A．B．C．D．不能确定
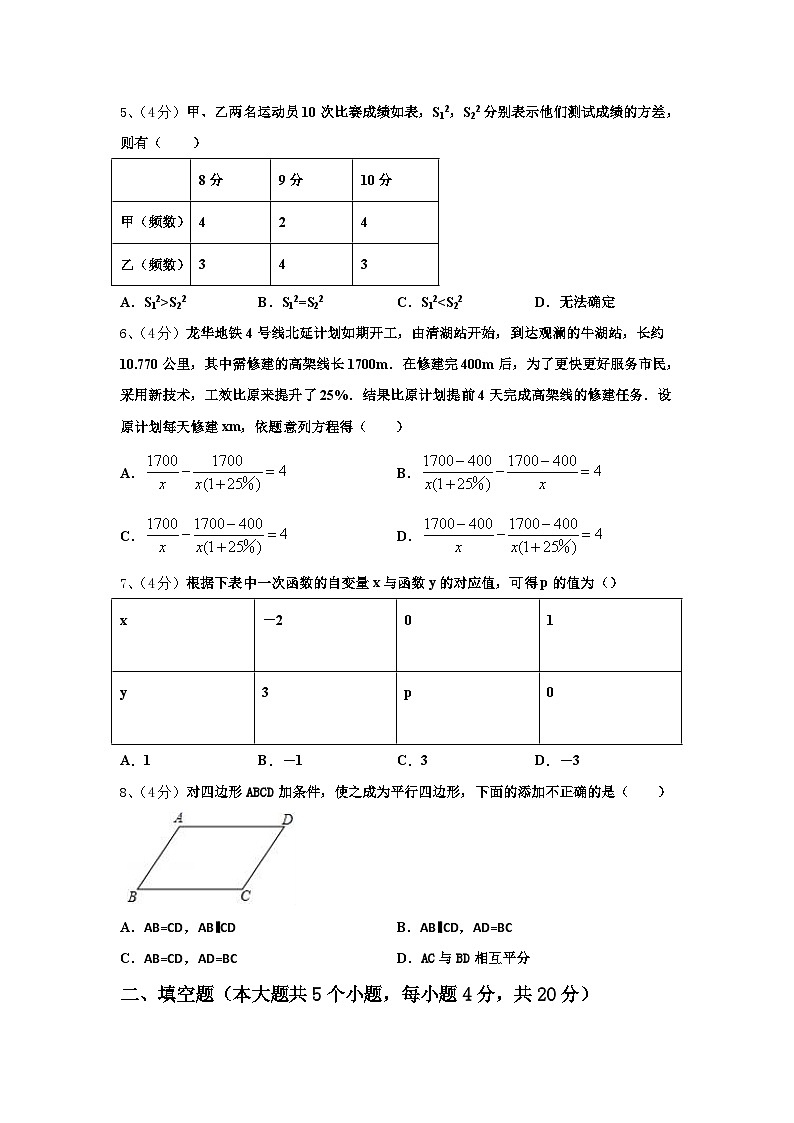
2、（4分）如图，将点P(-2，3)向右平移n个单位后落在直线y=2x-1上的点P'处，则n等于( )
A．4B．5C．6D．7
3、（4分）小明做了四道题：；；；；做对的有（ ）
A．B．C．D．
4、（4分）已知直角三角形的两条直角边的长分别是1，，则斜边长为（ ）
A．1B．C．2D．3
5、（4分）甲、乙两名运动员10次比赛成绩如表，S12，S22分别表示他们测试成绩的方差，则有（ ）
A．S12>S22B．S12=S22C．S126、（4分）龙华地铁4号线北延计划如期开工，由清湖站开始，到达观澜的牛湖站，长约10.770公里，其中需修建的高架线长1700m．在修建完400m后，为了更快更好服务市民，采用新技术，工效比原来提升了25%．结果比原计划提前4天完成高架线的修建任务．设原计划每天修建xm，依题意列方程得（ ）
A．B．
C．D．
7、（4分）根据下表中一次函数的自变量x与函数y的对应值，可得p的值为（）
A．1B．－1C．3D．－3
8、（4分）对四边形ABCD加条件，使之成为平行四边形，下面的添加不正确的是（ ）
A．AB=CD，AB∥CDB．AB∥CD，AD=BC
C．AB=CD，AD=BCD．AC与BD相互平分
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）若把分式中的x，y都扩大5倍，则分式的值____________．
10、（4分）正方形A1B1C1O、A2B2C2C1、A3B3C3C2…按如图的方式放置，A1、A2、A3…和点C1、C2、C3…分别在直线y＝x+2和x轴上，则点∁n的横坐标是_____．（用含n的代数式表示）
11、（4分）如图，在平面直角坐标系中，矩形的边一条动直线分别与将于点，且将矩形分为面积相等的两部分，则点到动直线的距离的最大值为__________.
12、（4分）当时，__．
13、（4分）如图，某校根据学生上学方式的一次抽样调查结果，绘制出一个未完成的扇形统计图，若该校共有学生1500人，则据此估计步行的有_____．
三、解答题（本大题共5个小题，共48分）
14、（12分）某欢乐谷为回馈广大谷迷，在暑假期间推出学生个人门票优惠价，各票价如下：
某慈善单位欲购买三种类型的票共100张奖励品学兼优的留守学生，其中购买的B种票数是A种票数的3倍还多7张，C种票y张．
（1）直接写出y与x之间的函数关系式；
（2）设购票总费用为w元，求w（元）与x（张）之间的函数关系式；
（3）为方便学生游玩，计划购买的学生夜场票不低于20张，且每种票至少购买5张，则有几种购票方案？并指出哪种方案费用最少．
15、（8分）在现今“互联网+”的时代，密码与我们的生活已经紧密相连，密不可分．而诸如“123456”、生日等简单密码又容易被破解，因此利用简单方法产生一组容易记忆的6位数密码就很有必要了．有一种用“因式分解法产生的密码，方便记忆，其原理是：将一个多项式分解因式，如多项式：x3+2x2﹣x﹣2因式分解的结果为（x﹣1）（x+1）（x+2），当x＝18时，x﹣1＝17，x+1＝19，x+2＝20，此时可以得到数字密码1．
（1）根据上述方法，当x＝21，y＝7时，对于多项式x3﹣xy2分解因式后可以形成哪些数字密码？（写出两个）
（2）若多项式x3+（m﹣3n）x2﹣nx﹣21因式分解后，利用本题的方法，当x＝27时可以得到其中一个密码为242834，求m、n的值．
16、（8分）解不等式组：，并把不等式组的解集在数轴上表示出来.
17、（10分）如图，在△ABC中，∠ACB＝90°，AC＝8，BC＝1．CD⊥AB于点D．点P从点A出发，以每秒1个单位长度的速度沿线段AB向终点B运动．在运动过程中，以点P为顶点作长为2，宽为1的矩形PQMN，其中PQ＝2，PN＝1，点Q在点P的左侧，MN在PQ的下方，且PQ总保持与AC垂直．设P的运动时间为t（秒）（t＞0），矩形PQMN与△ACD的重叠部分图形面积为S（平方单位）．
（1）求线段CD的长；
（2）当矩形PQMN与线段CD有公共点时，求t的取值范围；
（3）当点P在线段AD上运动时，求S与t的函数关系式．
18、（10分）已知（如图），点分别在边上，且四边形是菱形
（1）请使用直尺与圆规，分别确定点的具体位置（不写作法，保留画图痕迹）；
（2）如果，点在边上，且满足，求四边形的面积；
（3）当时，求的值。
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）如果一次函数y＝kx+2的函数值y随着x的值增大而减小，那么k的取值范围是_____．
20、（4分）若关于的一元二次方程有两个相等的实数根，则的值是__________．
21、（4分）若分式的值为0，则x的值为_______.
22、（4分）参加一次同学聚会，每两人都握一次手，所有人共握了45次，若设共有x人参加同学聚会．列方程得____．
23、（4分）一种病毒长度约为0.0000056mm，数据0.0000056用科学记数法可表示为______．
二、解答题（本大题共3个小题，共30分）
24、（8分）2019年中国北京世界园艺博览会于4月28日晚在北京·延庆隆重开幕，本届世园会主题为“绿色生活、美丽家园”．自开园以来，世园会迎来了世界各国游客进园参观．据统计，仅五一小长假前来世园会打卡的游客就总计约32.7万人次．其中中国馆也是非常受欢迎的场馆．据调查，中国馆5月1日游览人数约为4万人，5月3日游览人数约为9万人，若5月1日到5月3日游客人数的日增长率相同，求中国馆这两天游客人数的日平均增长率是多少？
25、（10分）甲、乙两家草莓采摘园的草莓品质相同，销售价格也相同．“五一期间”，两家均推出了优惠方案，甲采摘园的优惠方案是：游客进园需购买50元的门票，采摘的草莓六折优惠；乙采摘园的优惠方案是：游客进园不需购买门票，采摘园的草莓超过一定数量后，超过部分打折优惠．优惠期间，设某游客的草莓采摘量为x（千克），在甲采摘园所需总费用为（元），在乙采摘园所需总费用为（元），图中折线OAB表示与x之间的函数关系．
（1）甲、乙两采摘园优惠前的草莓销售价格是每千克 元；
（2）求、与x的函数表达式；
（3）在图中画出与x的函数图象，并写出选择甲采摘园所需总费用较少时，草莓采摘量x的范围．
26、（12分）计算
（1）
（2）
（3）
（4）（+3﹣2）×2
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、A
【解析】
根据：正比例函数，y随x增大而减小；，y随x增大而增大.
【详解】
因为正比例函数，
所以，y随x增大而减小，
因为，图象上两点、，且，
所以，
故选A
本题考核知识点：正比例函数. 解题关键点：理解正比例函数性质.
2、A
【解析】
由平移的性质得出P'的坐标，把P'点坐标代入直线y=2x-1上即可求出n的值；
【详解】
由题意得P'(-2+n,3)，
则3=2(-2+n)-1，
解得n=4.
故答案为A.
本题主要考查了一次函数的图象，平移的性质，掌握一次函数的图象，平移的性质是解题的关键.
3、D
【解析】
根据无理数的运算法则，逐一计算即可.
【详解】
，正确；
，错误；
，错误；
，正确；
故答案为D.
此题主要考查无理数的运算，熟练掌握，即可解题.
4、C
【解析】
根据勾股定理进行计算，即可求得结果．
【详解】
解：直角三角形的两条直角边的长分别为1，，
则斜边长＝=2；
故选C．
本题考查了勾股定理；熟练运用勾股定理进行求解是解决问题的关键．
5、A
【解析】
根据题意以及图表所示，先求出甲和乙成绩的平均数，然后运用方差公式即可做出选择．
【详解】
由表可知，甲的成绩平均数为，乙的成绩的平均数为，所以甲的成绩的方差为,乙的方差为，所以＞．
故本题选择A．
本题主要考查方差公式的运用，根据图中数据，掌握方差公式即可求解．
6、C
【解析】
设原计划每天修建xm，则实际每天修建（1+25%）xm，根据题意可得，增加工作效率之后比原计划提前4天完成任务，据此列方程.
【详解】
解：设原计划每天修建xm，则实际每天修建（1+25%）xm，由题意得：

故选C.
7、A
【解析】
设一次函数的解析式为y=kx+b，将表格中的对应的x,y的值（－2，3），（1，0）代入得：
，解得：．
∴一次函数的解析式为y=－x+1．
当x=0时，得y=1．故选A．
8、B
【解析】
分析：根据平行四边形的判定定理即可得到结论.
详解：∵AB=CD,AB∥CD,
∴四边形ABCD是平行四边形,
∵AB∥CD,AD=BC, ∴四边形ABCD是平行四边形或梯形,
∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形,
∵AC与BD相互平分,
∴四边形ABCD是平行四边形,
故选B.
点睛：本题考查了平行四边形的判定，熟练掌握平行四边形的判定定理是解题的关键.
二、填空题（本大题共5个小题，每小题4分，共20分）
9、扩大5倍
【解析】
【分析】把分式中的x和y都扩大5倍，分别用5x和5y去代换原分式中的x和y，利用分式的基本性质化简即可．
【详解】把分式中的x，y都扩大5倍得：
=，
即分式的值扩大5倍，
故答案为：扩大5倍.
【点睛】本题考查了分式的基本性质，根据分式的基本性质，无论是把分式的分子和分母扩大还是缩小相同的倍数，都不要漏乘（除）分子、分母中的任何一项．
10、
【解析】
观察图像，由直线y＝x+2和正方形的关系，即可得出规律，推导出Cn的横坐标.
【详解】
解：根据题意，由图像可知，，
正方形A1B1C1O、 A2B2C2C1
，直线y＝x+2的斜率为1，则
以此类推，，
此题主要考查一次函数图像的性质和正方形的关系，推导得出关系式.
11、
【解析】
设M,N为CO,EF中点, 点到动直线的距离为ON,求解即可.
【详解】
∵
∴SOABC=12
∵将矩形分为面积相等的两部分
∴SCEOF=×（CE+OF）×2=6
∴CE+OF=6
设M,N为CO,EF中点，
∴MN=3
点到动直线的距离的最大值为ON=
故答案.
本题考查的是的动点问题，熟练掌握最大距离的算法是解题的关键
12、
【解析】
将x的值代入x2-2x+2028=（x-1）2+2027，根据二次根式的运算法则计算可得．
【详解】
解：当x=1-时，
x2-2x+2028=（x-1）2+2027
=（1--1）2+2027
=（-）2+2027，
=3+2027
=1，
故答案为：1．
本题主要考查二次根式的化简求值，解题的关键是掌握二次根式的性质和运算法则及完全平方公式．
13、1
【解析】
∵骑车的学生所占的百分比是×100%=35%，
∴步行的学生所占的百分比是1﹣10%﹣15%﹣35%=40%，
∴若该校共有学生1500人，则据此估计步行的有1500×40%=1（人），
故答案为1．
三、解答题（本大题共5个小题，共48分）
14、（1）y=93-4x；（2）w=-160x+14790；(3) 共有3种购票方案, 当A种票为22张，B种票73张，C种票为5张时费用最少，最少费用为11270元．
【解析】
试题分析：（1）根据总票数为100得到x+3x+7+y=100，然后用x表示y即可；
（2）利用表中数据把三种票的费用加起来得到w=80x+120（3x+7）+150（93-4x），然后整理即可；
（3）根据题意得到，再解不等式组且确定不等式组的整数解为20、21、22，于是得到共有3种购票方案，然后根据一次函数的性质求w的最小值．
试题解析：解：（1）x+3x+7+y=100，
所以y=93-4x；
（2）w=80x+120（3x+7）+150（93-4x）
=-160x+14790；
（3）依题意得，
解得20≤x≤22，
因为整数x为20、21、22，
所以共有3种购票方案（A、20，B、67，C、13；A、21，B、70，C、9；A、22，B、73，C、5）；
而w=-160x+14790，
因为k=-160＜0，
所以y随x的增大而减小，
所以当x=22时，y最小=22×（-160）+14790=11270，
即当A种票为22张，B种票73张，C种票为5张时费用最少，最少费用为11270元．
考点：1.一次函数的应用；2.一元一次不等式组的应用．
15、（1）可以形成的数字密码是：212814、211428；（2）m的值是56，n的值是2．
【解析】
（1）先将多项式进行因式分解，然后再根据数字密码方法形成数字密码即可；（2）设x3+（m﹣3n）x2﹣nx﹣21＝（x+p）（x+q）（x+r），当x＝27时可以得到其中一个密码为242834，得到方程解出p、q、r，然后回代入原多项式即可求得m、n
【详解】
（1）x3﹣xy2＝x（x2﹣y2）＝x（x+y）（x﹣y），
当x＝21，y＝7时，x+y＝28，x﹣y＝14，
∴可以形成的数字密码是：212814、211428；
（2）设x3+（m﹣3n）x2﹣nx﹣21＝（x+p）（x+q）（x+r），
∵当x＝27时可以得到其中一个密码为242834，
∴27+p＝24，27+q＝28，27+r＝34，
解得，p＝﹣3，q＝1，r＝7，
∴x3+（m﹣3n）x2﹣nx﹣21＝（x﹣3）（x+1）（x+7），
∴x3+（m﹣3n）x2﹣nx﹣21＝x3+5x2﹣2x﹣21，
∴ 得，
即m的值是56，n的值是2．
本题属于阅读理解题型，考查知识点以因式分解为主，本题第一问关键在于理解题目中给到的数字密码的运算规则，第二问的关键在于能够将原多项式设成（x+p）（x+q）（x+r），解出p、q、r
16、；数轴表示见解析.
【解析】
先把两个不等式分别求出来，然后根据不等式的解的口诀得到不等式的解集，然后把解集表示在数轴上即可.
【详解】
解：，
解不等式①，得：，
解不等式②，得：，
∴不等式的解集为：，
在数轴上表示为：
本题考查了解一元一次不等式组，解题的关键是正确解出每一个不等式，然后掌握求解集的口诀.
17、（1）CD＝；（2）≤t≤；（3）当0＜t＜时，S＝；当≤t≤时，S＝2；当＜t≤时，S=-t2+t-．
【解析】
（1）由勾股定理得出AB＝,由△ABC的面积得出AC•BC＝AB•CD，即可得出CD的长；
（2）分两种情形：①当点N在线段CD上时，如图1所示，利用相似三角形的性质求解即可．②当点Q在线段CD上时，如图2所示，利用相似三角形的性质求解即可．
（3）首先求出点Q落在AC上的运动时间t，再分三种情形：①当0＜t＜时，重叠部分是矩形PHYN，如图4所示，②当≤t≤时，重合部分是矩形PQMN，S＝PQ•PN＝2．③当＜t≤时，如图5中重叠部分是五边形PQMJI，分别求解即可．
【详解】
（1）∵∠ACB＝90°，AC＝8，BC＝1，
∴AB＝，
∵S△ABC＝AC•BC＝AB•CD，
∴AC•BC＝AB•CD，即：8×1＝10×CD，
∴CD＝；
（2）在Rt△ADC中，AD＝，BD＝AB－AD＝10－＝，
当点N在线段CD上时，如图1所示：
∵矩形PQMN，PQ总保持与AC垂直，
∴PN∥AC，
∴∠NPD＝∠CAD，
∵∠PDN＝∠ADC，
∴△PDN∽△ADC，
∴，即：，
解得：PD＝，
∴t＝AD－PD＝，
当点Q在线段CD上时，如图2所示：
∵PQ总保持与AC垂直，
∴PQ∥BC，△DPQ∽△DBC，
∴，即：，
解得：DP＝ ，
∴t＝AD+DP＝，
∴当矩形PQMN与线段CD有公共点时，t的取值范围为≤t≤；
（3）当Q在AC上时，如图3所示：
∵PQ总保持与AC垂直，
∴PQ∥BC，△APQ∽△ABC，
∴，即：，
解得：AP＝ ，
当0＜t＜时，重叠部分是矩形PHYN，如图4所示：
∵PQ∥BC，
∴△APH∽△ABC，
∴，即：，
∴PH＝，
∴S＝PH•PN＝；
当≤t≤时，重合部分是矩形PQMN，S＝PQ•PN＝2．
当＜t≤时，如图5中重叠部分是五边形PQMJI，
S＝S矩形PNMQ-S△JIN＝2- •（t-）[1-（-t）•]＝-t2+t-．
【点评】
本题属于四边形综合题，考查了解直角三角形，矩形的性质，相似三角形的判定和性质，多边形的面积等知识，解题的关键是学会用分类讨论的思想思考问题.
18、（1）详见解析；（2）；（3）
【解析】
（1）作△ABC的角平分线AE，作线段AE的垂直平分线交AB于D，交AC于F，连接DE、EF，四边形ADEF即为所求；
（2）由题意，当∠A=60°，AD=4时，△ADF，△EFD，△EMD都是等边三角形，边长为4，由此即可解决问题；
（3）利用三角形的中位线定理即可解决问题．
【详解】
（1）D，E，F的位置如图所示．
（2）由题意，当∠A=60°，AD=4时，△ADF，△EFD，△EMD都是等边三角形，边长为4，
∴S四边形AFEM=3××42=12；
（3）当AB=AC时，易知DE是△ABC的中位线，
∴DE=AC
∴=．
本题考查菱形的判定和性质，复杂作图，等边三角形的性质，三角形的中位线定理等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．
一、填空题（本大题共5个小题，每小题4分，共20分）
19、k＜1．
【解析】
根据一次函数的性质解答即可.
【详解】
∵一次函数y＝kx+2，函数值y随x的值增大而减小，
∴k＜1．
故答案为：k＜1．
本题考查了一次函数的图像与性质，对于一次函数y=kx+b（k为常数，k≠1）,当k>1时，y随x的增大而增大；当k<1时，y随x的增大而减小.
20、1
【解析】
因为关于的一元二次方程有两个相等的实数根，故 ，代入求解即可.
【详解】
根据题意可得： 解得：m=1
故答案为：1
本题考查的是一元二次方程的根的判别式，掌握根的判别式与方程的根的关系是关键.
21、-1
【解析】
根据分式的值为零的条件可以求出x的值．
【详解】
解：根据题意得：，
解得：x=-1．
故答案为：-1.
若分式的值为零，需同时具备两个条件：（1）分子为2；（2）分母不为2．这两个条件缺一不可．
22、 x（x﹣1）=1
【解析】
利用一元二次方程应用中的基本数量关系：x人参加聚会，两人只握一次手，握手总次数为 x（x-1）解决问题即可．
【详解】
由题意列方程得，
x（x-1）=1．
故答案为：x（x-1）=1．
本题考查了一元二次方程的应用，熟知x人参加聚会，两人只握一次手，握手总次数为 x（x-1）这一基本数量关系是解题的关键.
23、5.1×10-1
【解析】
绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10-n，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．
【详解】
解：0.0000051=5.1×10-1．
故答案为：5.1×10-1．
本题考查用科学记数法表示较小的数，一般形式为a×10-n，其中1≤|a|＜10，n为由原数左边起第一个不为零的数字前面的0的个数所决定．
二、解答题（本大题共3个小题，共30分）
24、50%．
【解析】
设中国馆这两天游客人数的日平均增长率为x，根据中国馆5月1日游览人数约为4万人，5月3日游览人数约为9万人，若5月1日到5月3日游客人数的日增长率相同，列出方程即可.
【详解】
解：设中国馆这两天游客人数的日平均增长率为x，由题意得：

解得，（舍去）
答：中国馆这两天游客人数的日平均增长率为50%．
此题考查一元二次方程的应用，解题关键在于列出方程.
25、（1）1；（2），；（3）＜x＜．
【解析】
试题分析：（1）根据单价=总价÷数量，即可解决问题．
（2）y1函数表达式=50+单价×数量，y2与x的函数表达式结合图象利用待定系数法即可解决．
（3）画出函数图象后y1在y2下面即可解决问题．
试题解析：（1）甲、乙两采摘园优惠前的草莓销售价格是每千克10÷10=1元．
故答案为1．
（2）由题意，；
（3）函数y1的图象如图所示，由解得：，所以点F坐标（，125），由，解得：，所以点E坐标（，650）．
由图象可知甲采摘园所需总费用较少时＜x＜．
考点：分段函数；函数最值问题．
26、（1）（2）（3） （4）1+1
【解析】
分析：(1)先将二次根式化为最简,然后再进行二次根式的除法及减法运算.(2) 运用平方差及完全平方式解答即可.(3) 将二次根式化为最简,然后再进行同类二次根式的合并即可.(4) 先将二次根式化为最简,然后再进行二次根式的乘法运算.
详解：（1）原式＝
（2）原式＝
（3）原式=2﹣2+﹣=﹣；
（4）（+3﹣2）×2=（+）×2=1+1．
点睛：本题考查了二次根式的计算,熟练化简二次根式后,在加减的过程中,有同类二次根式的要合并;相乘的时候,被开方数简单的直接让被开方数相乘,再化简;较大的也可先化简,再相乘,灵活对待.
题号
一
二
三
四
五
总分
得分
批阅人
8分
9分
10分
甲（频数）
4
2
4
乙（频数）
3
4
3
x
－2
0
1
y
3
p
0
票价种类
（A）学生夜场票
（B）学生日通票
（C）节假日通票
单价（元）
80
120
150