

上海外国语大学附属外国语学校 2024-2025学年九年级上学期第一次月考数学试卷
展开1.如图,在△ABC中,点D、E分别在边AB、AC上,DE∥BC,AD:BD=1:2,那么S△ABE:S△ABC= .
2.如图,直线l1∥l2∥l3,若,EF=9,则DF的长度为 .
3.已知,点P、Q是线段AB的两个黄金分割点,若AB=8,则PQ的长是 .
4.已知(﹣1,y1),(2,y2),(4,y3)都是二次函数y=ax2﹣2ax+3a(a≠0)的图像上的点,当x>2时,y随着x的增大而增大,则y1,y2,y3按从小到大顺序排列是 .
5.已知抛物线C:y=x2+3x﹣10,将抛物线C平移得到抛物线C',若两条抛物线C,C′关于直线x=1对称,那么应将抛物线C向 平移 个单位.
6.已知非零实数x,y,z满足,则的值为 .
7.如图,AD是△ABC的中线,AE=EF=FC,BE交AD于点G,则= .
8.二次函数y=ax2+bx+c的图象与x轴有两个交点M、N,顶点为R,若△MNR恰好是等边三角形,则b2﹣4ac= .
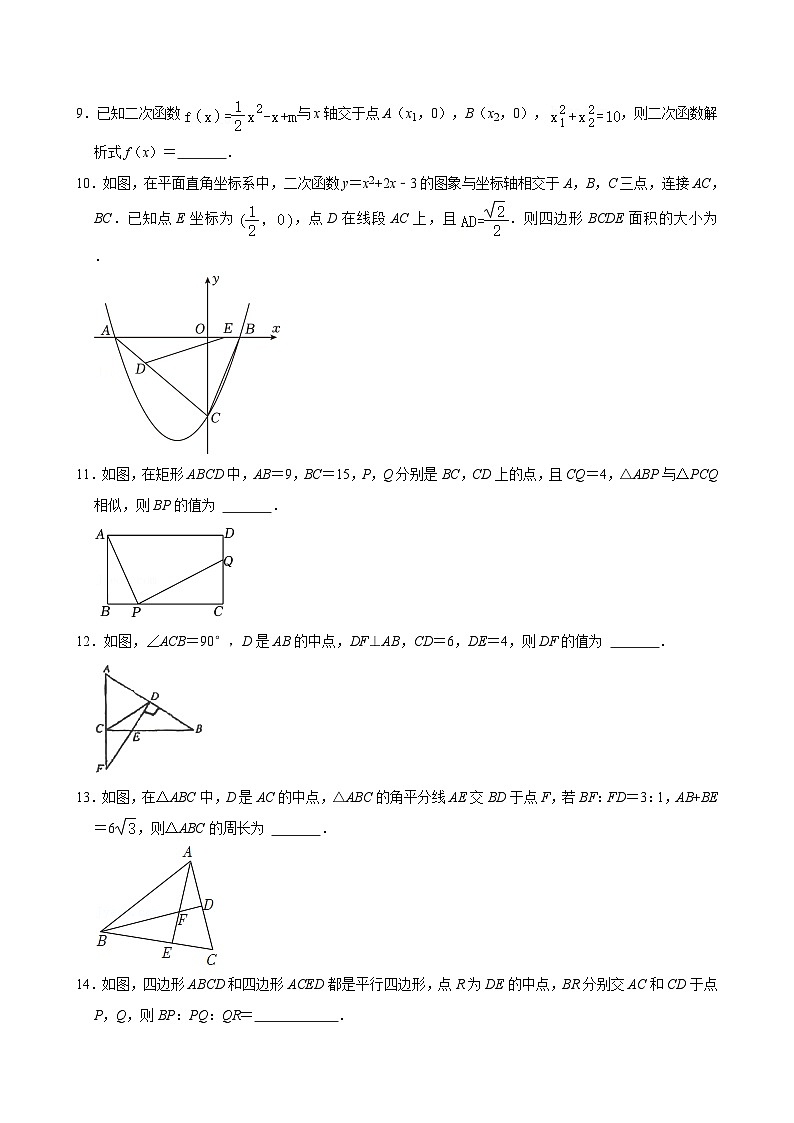
9.已知二次函数与x轴交于点A(x1,0),B(x2,0),,则二次函数解析式f(x)= .
10.如图,在平面直角坐标系中,二次函数y=x2+2x﹣3的图象与坐标轴相交于A,B,C三点,连接AC,BC.已知点E坐标为,点D在线段AC上,且.则四边形BCDE面积的大小为 .
11.如图,在矩形ABCD中,AB=9,BC=15,P,Q分别是BC,CD上的点,且CQ=4,△ABP与△PCQ相似,则BP的值为 .
12.如图,∠ACB=90°,D是AB的中点,DF⊥AB,CD=6,DE=4,则DF的值为 .
13.如图,在△ABC中,D是AC的中点,△ABC的角平分线AE交BD于点F,若BF:FD=3:1,AB+BE=6,则△ABC的周长为 .
14.如图,四边形ABCD和四边形ACED都是平行四边形,点R为DE的中点,BR分别交AC和CD于点P,Q,则BP:PQ:QR= .
15.如图,在△ABC中,AC=BC,D为AB的中点,F为BC边上一点,连接CD、AF交于点E.若∠FAC=90°﹣3∠BAF,BF:AC=2:5,EF=2,则AB长为 .
16.如图,△ABC中,∠BCA=90°,AB=2AC,点P在△ABC内,且PA=,PB=5,PC=2,则△ABC的面积为 .
二、选择题(共4题,每题2分,共8分)
17.下列说法正确的是( )
A.任意两个菱形都相似
B.任意两个正方形都相似
C.任意两个等腰三角形都相似
D.任意两个矩形都相似
18.若(b、d、f均为正数),则下列式子不一定成立的是( )
A.B.
C.D.
19.定义[a,b,c]为函数y=ax2+bx+c的特征数,下面给出特征数为[2m,1﹣m,﹣1﹣m]的函数的一些结论:(1)当m=﹣3时,函数图像的顶点坐标是;(2)当m>0时,函数图像截x轴所得的线段长度大于;(3)当m<0时,函数在时,y随x的增大而减小;(4)当m≠0时,无论m取何值函数图像经过定点.其中正确的结论有( )个.
A.0B.1C.2D.3
20.如图,四边形ABCD和AGFE均为正方形,若,则CF的长为( )
A.B.2C.2D.3
三、解答题(共6题,共52分)
21.已知二次函数y=(m2﹣2)x2﹣4mx+n的图象的对称轴是直线x=2,且最高点在直线y=x+1上,求这个二次函数的表达式.
22.如图,王华晚上由路灯A下的B处走到C处时,测得影子CD的长为1米,继续往前走3米到达E处时,测得影子EF的长为2米,已知王华的身高是1.5米,那么路灯A的高度AB是多少?
23.已知:如图,二次函数y=x2+bx的图像交x轴正半轴于点A,顶点为P,一次函数的图像交x轴于点B,交y轴于点C,.
(1)求二次函数顶点P坐标;
(2)将二次函数图像向下平移m(m>0)个单位,设平移后抛物线顶点为P',若S△ABP′=S△BCP',求m的值.
24.已知如图,D是△ABC的边AB上一点,DE∥BC,交边AC于点E,延长DE至点F,使EF=DE,连接BF,交边AC于点G,连接CF
(1)求证:=;
(2)如果CF2=FG•FB,求证:CG•CE=BC•DE.
25.如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a<0)与x轴交于A(﹣2,0)、B(4,0)两点,与y轴交于点C,且OC=2OA.
(1)试求抛物线的解析式;
(2)直线y=kx+1(k>0)与y轴交于点D,与抛物线交于点P,与直线BC交于点M,记m=,试求m的最大值及此时点P的坐标;
(3)在(2)的条件下,点Q是x轴上的一个动点,点N是坐标平面内的一点,是否存在这样的点Q、N,使得以P、D、Q、N四点组成的四边形是矩形?如果存在,请求出点N的坐标;如果不存在,请说明理由.
26.已知,在矩形ABCD中,点M是边AB上的一个点(与点A、B不重合),联结CM,作∠CMF=90°,且MF分别交边AD于点E、交边CD的延长线于点F.点G为线段MF的中点,联结DG.
(1)如图1,如果AD=AM=4,当点E与点G重合时,求△MFC的面积;
(2)如图2,如果AM=2,BM=4.当点G在矩形ABCD内部时,设AD=x,DG2=y,求y关于x的函数解析式,并写出定义域;
(3)如果AM=6,CD=8,∠F=∠EDG,求线段AD的长.(直接写出计算结果)
2023-2024学年上海外国语大学附属外国语学校八年级(上)期末数学试卷(含详细答案解析): 这是一份2023-2024学年上海外国语大学附属外国语学校八年级(上)期末数学试卷(含详细答案解析),共25页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。
+上海外国语大学松江外国语学校2023-2024学年九年级上学期月考数学试卷(9月份)+: 这是一份+上海外国语大学松江外国语学校2023-2024学年九年级上学期月考数学试卷(9月份)+,共26页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
03, 上海外国语大学松江外国语学校2023-2024学年九年级上学期月考数学试卷(9月份): 这是一份03, 上海外国语大学松江外国语学校2023-2024学年九年级上学期月考数学试卷(9月份),共24页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












