

大连市重点中学2025届数学九年级第一学期开学学业水平测试模拟试题【含答案】
展开一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求)
1、(4分)如图,矩形ABCD中,对角线AC,BD交于点O,E,F分别是边BC,AD的中点,AB=2,BC=4,一动点P从点B出发,沿着B﹣A﹣D﹣C在矩形的边上运动,运动到点C停止,点M为图1中某一定点,设点P运动的路程为x,△BPM的面积为y,表示y与x的函数关系的图象大致如图2所示.则点M的位置可能是图1中的( )
A.点CB.点OC.点ED.点F
2、(4分)用科学记数法表示,结果为( )
A.B.C.D.
3、(4分)在平行四边形ABCD中,∠B=60°,那么下列各式中,不能成立的是( )
A.∠D=60°B.∠A=120°C.∠C+∠D=180°D.∠C+∠A=180°
4、(4分)某服装制造厂要在开学前赶制套校服,为了尽快完成任务,厂领导合理调配加强第一线人力,使每天完成的校服比原计划多,结果提前天完成任务,问:原计划每天能完成多少套校服?设原来每天完成校服套,则可列出方程( )
A.B.
C.D.
5、(4分)△ABC中∠A、∠B、∠C的对边分别是a、b、c,下列命题中的假命题是( )
A.如果∠C﹣∠B=∠A,则△ABC是直角三角形
B.如果c2=b2﹣a2,则△ABC是直角三角形,且∠C=90°
C.如果(c+a)(c﹣a)=b2,则△ABC是直角三角形
D.如果∠A:∠B:∠C=5:2:3,则△ABC是直角三角形
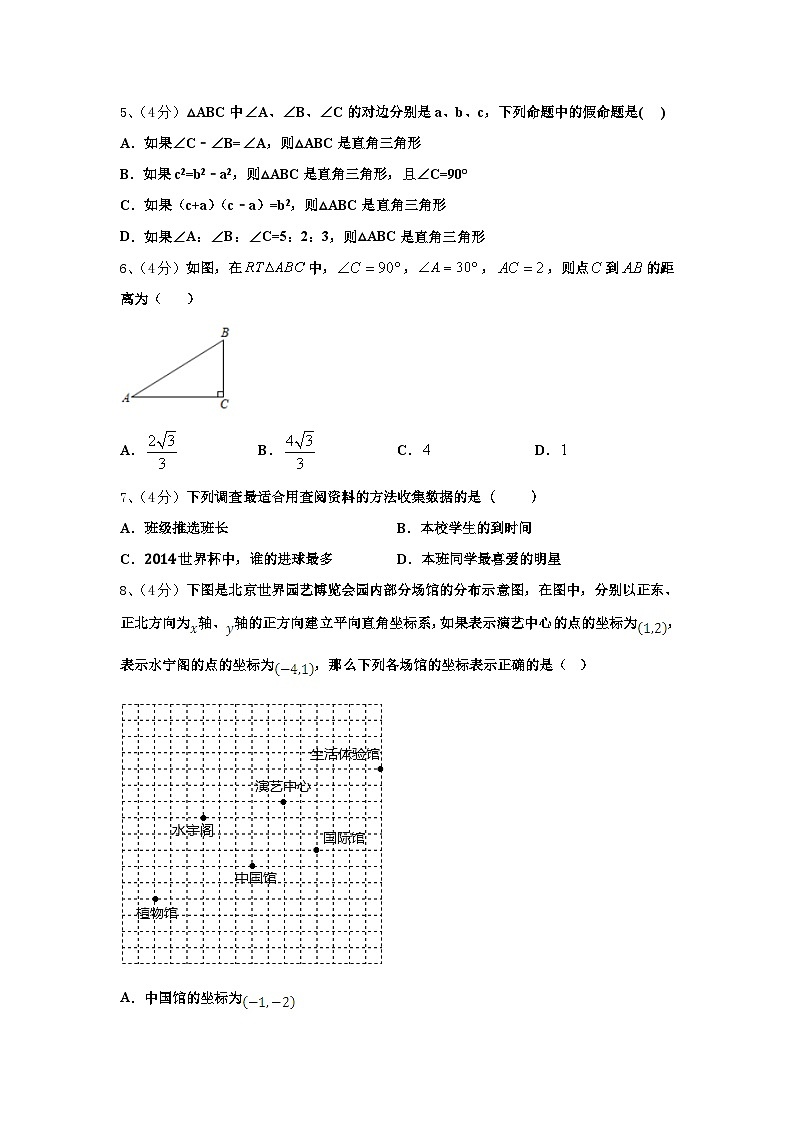
6、(4分)如图,在中,,,,则点到的距离为( )
A.B.C.D.
7、(4分)下列调查最适合用查阅资料的方法收集数据的是( )
A.班级推选班长B.本校学生的到时间
C.2014世界杯中,谁的进球最多D.本班同学最喜爱的明星
8、(4分)下图是北京世界园艺博览会园内部分场馆的分布示意图,在图中,分别以正东、正北方向为轴、轴的正方向建立平向直角坐标系,如果表示演艺中心的点的坐标为,表示水宁阁的点的坐标为,那么下列各场馆的坐标表示正确的是( )
A.中国馆的坐标为
B.国际馆的坐标为
C.生活体验馆的坐标为
D.植物馆的坐标为
二、填空题(本大题共5个小题,每小题4分,共20分)
9、(4分)已知关于x的方程x2+(3﹣2k)x+k2+1=0的两个实数根分别是x1、x2,当|x1|+|x2|=7时,那么k的值是__.
10、(4分)如图所示,平行四边形中,点在边上,以为折痕,将向上翻折,点正好落在上的处,若的周长为8,的周长为22,则的长为__________.
11、(4分)把方程x2+4xy﹣5y2=0化为两个二元一次方程,它们是_____和_____.
12、(4分)已知α、β是一元二次方程x2﹣2019x+1=0的两实根,则代数式(α﹣2019)(β﹣2019)=_____.
13、(4分)如图,将菱形纸片ABCD折叠,使点B落在AD边的点F处,折痕为CE,若∠D=70°,则∠ECF的度数是_________.
三、解答题(本大题共5个小题,共48分)
14、(12分)如图,四边形ABCD中,AD∥BC,AE⊥AD交BD于点E,CF⊥BC交BD于点F,且AE=CF,
求证:四边形ABCD是平行四边形.
15、(8分)如图,将边长为 4 的正方形 ABCD 沿其对角线 AC 剪开,再把△ABC沿着 AD 方向平移,得到 △ABC .
(1)当两个三角形重叠部分的面积为 3 时,求移动的距离 AA ;
(2)当移动的距离 AA 是何值时,重叠部分是菱形.
16、(8分)在三个整式x2+2xy,y2+2xy,x2中,请你任意选出两个进行加(或减)运算,使所得整式可以因式分解,并进行因式分解.
17、(10分)如图,□ABCD的对角线AC、BD相交于点O,AC平分∠BAD,DP//AC,CP//BD.
(1)求证:四边形ABCD是菱形;
(2)若AC=4,BD=6,求OP的长.
18、(10分)问题背景:如图1:在四边形ABCD中,AB=AD,∠BAD=120∘ ,∠B=∠ADC=90°.E、F分别是 BC,CD 上的点.且∠EAF=60° . 探究图中线段BE,EF,FD 之间的数量关系. 小王同学探究此问题的方法是,延长 FD 到点 G,使 DG=BE,连结 AG,先证明△ABE≌△ADG, 再证明△AEF≌△AGF,可得出结论,他的结论应是_________;
探索延伸:如图2,若四边形ABCD中,AB=AD,∠B+∠D=180° .E,F 分别是 BC,CD 上的点,且∠EAF=∠BAD,上述结论是否仍然成立,并说明理由;
实际应用:如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东 70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以55 海里/小时的速度前进,舰艇乙沿北偏东 50°的方向以 75 海里/小时的速度前进2小时后, 指挥中心观测到甲、乙两舰艇分别到达 E,F 处,且两舰艇之间的夹角为70° ,试求此时两舰 艇之间的距离.
B卷(50分)
一、填空题(本大题共5个小题,每小题4分,共20分)
19、(4分)如图,在中,,,的面积是,边的垂直平分线分别交,边于点,.若点为边的中点,点为线段上一动点,则周长的最小值为__________.
20、(4分)如果,那么的值是___________.
21、(4分)如图,将绕着直角顶点顺时针旋转,得到,连接,若,则__________度.
22、(4分)分解因式:m2﹣9m=_____.
23、(4分)如图,在直角三角形中,,、、分别是、、的中点,若=6厘米,则的长为_________.
二、解答题(本大题共3个小题,共30分)
24、(8分)化简分式:.
25、(10分)如图,某住宅小区在施工过程中留下了一块空地,已知AD=4米,CD=3米,∠ADC=90°,AB=13米,BC=12米,小区为美化环境,欲在空地上铺草坪,已知草坪每平方米100元,试问用该草坪铺满这块空地共需花费多少元?
26、(12分)已知非零实数满足,求的值.
参考答案与详细解析
一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求)
1、B
【解析】
从图2中可看出当x=6时,此时△BPM的面积为0,说明点M一定在BD上,选项中只有点O在BD上,所以点M的位置可能是图1中的点O.
【详解】
解:∵AB=2,BC=4,四边形ABCD是矩形,
∴当x=6时,点P到达D点,此时△BPM的面积为0,说明点M一定在BD上,
∴从选项中可得只有O点符合,所以点M的位置可能是图1中的点O.
故选:B.
本题主要考查了动点问题的函数图象,解题的关键是找出当x=6时,此时△BPM的面积为0,说明点M一定在BD上这一信息.
2、B
【解析】
小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
【详解】
﹣0.000 001 4=﹣1.4×10﹣1.
故选B.
本题考查了用科学记数法表示较小的数.一般形式为a×10﹣n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.
3、D
【解析】
解:∵四边形ABCD是平行四边形,∴∠D=∠B=60°.故A正确;
∵AD∥BC,∴∠A+∠B=180°,∴∠A=180°-∠B=120°,故B正确;
∵AD∥BC,∴∠C+∠D=180°,故C正确;
∵四边形ABCD是平行四边形,∴∠C=∠A=120°,故D不正确,
故选D.
4、C
【解析】
由实际每天完成的校服比原计划多得到实际每天完成校服x(1+20%)套,再根据提前4天完成任务即可列出方程.
【详解】
∵原来每天完成校服套,实际每天完成的校服比原计划多,
∴实际每天完成校服x(1+20%)套,
由题意得,
故选:C.
此题考查分式方程的实际应用,正确理解题意是解题的关键.
5、B
【解析】
直角三角形的判定方法有:①求得一个角为90°,②利用勾股定理的逆定理.
【详解】
解:A、∵∠C+∠B+∠A=180°(三角形内角和定理),∠C﹣∠B=∠A,∴∠C+∠B+(∠C﹣∠B)=180°,∴2∠C=180°,∴∠C=90°,故该选项正确,
B、如果c2=b2﹣a2,则△ABC是直角三角形,且∠B=90°,故该选项错误,
C、化简后有c2=a2+b2,则△ABC是直角三角形,故该选项正确,
D、设三角分别为5x,3x,2x,根据三角形内角和定理可得,5x+3x+2x=180°,则x=18°,所以这三个角分别为:90度,36度,54度,则△ABC是直角三角形,故该选项正确.
故选B.
考查了命题与定理的知识,解题的关键是了解直角三角形的判定方法.
6、D
【解析】
根据直角三角形的性质、勾股定理分别求出AB、BC,根据三角形的面积公式计算即可.
【详解】
解:设点C到AB的距离为h,
∵∠C=90°,∠A=30°,
∴AB=2BC,
由勾股定理得,AB2-BC2=AC2,即(2BC)2-BC2=22,
解得,BC=,
则AB=2BC=,
由三角形的面积公式得,
,
解得,h=1,
故选:D.
本题考查的是直角三角形的性质,掌握在直角三角形中,30°角所对的直角边等于斜边的一半是解题的关键.
7、C
【解析】
了解收集数据的方法及渠道,得出最适合用查阅资料的方法收集数据的选项.
【详解】
A、B、D适合用调查的方法收集数据,不符合题意;
C适合用查阅资料的方法收集数据,符合题意.
故选C.
本题考查了调查收集数据的过程与方法.解题关键是掌握收集数据的几种方法:查资料、做实验和做调查.
8、A
【解析】
根据演艺中心的点的坐标为(1,2),表示水宁阁的点的坐标为(-4,1)确定坐标原点的位置,建立平面直角坐标系,进而可确定其它点的坐标.
【详解】
解:根据题意可建立如下所示平面直角坐标系,
A、中国馆的坐标为(-1,-2),故本选项正确;
B、国际馆的坐标为(3,-1),故本选项错误;
C、生活体验馆的坐标为(7,4),故本选项错误;
D、植物馆的坐标为(-7,-4),故本选项错误.
故选:A.
此题考查坐标确定位置,解题的关键就是确定坐标原点和x,y轴的位置.
二、填空题(本大题共5个小题,每小题4分,共20分)
9、﹣1.
【解析】
先根据方程有两个实数根,确定△≥0,可得k≤,由x1•x1=k1+1>0,可知x1、x1,同号,分情况讨论即可.
【详解】
∵x1+(3﹣1k)x+k1+1=0的两个实数根分别是x1、x1,
∴△=(3﹣1k)1﹣4×1×(k1+1)≥0,
9﹣11k+4k1﹣4k1﹣4≥0,
k≤,
∵x1•x1=k1+1>0,
∴x1、x1,同号,
分两种情况:
①当x1、x1同为正数时,x1+x1=7,
即1k﹣3=7,
k=5,
∵k≤,
∴k=5不符合题意,舍去,
②当x1、x1同为负数时,x1+x1=﹣7,
即1k﹣3=﹣7,
k=﹣1,
故答案为:﹣1.
本题考查了根与系数的关系和根的判别式.解此题时很多学生容易顺理成章的利用两根之积与和公式进行解答,解出k值,而忽略了限制性条件△≥0时k≤.
10、1.
【解析】
依据△FDE的周长为8,△FCB的周长为22,即可得出DF+AD=8,FC+CB+AB=22,进而得到平行四边形ABCD的周长=8+22=30,可得AB+BC=BF+BC=15,再根据△FCB的周长=FC+CB+BF=22,即可得到CF=22-15=1.
【详解】
解:由折叠可得,EF=AE,BF=AB.
∵△FDE的周长为8,△FCB的周长为22,
∴DF+AD=8,FC+CB+AB=22,
∴平行四边形ABCD的周长=8+22=30,
∴AB+BC=BF+BC=15,
又∵△FCB的周长=FC+CB+BF=22,
∴CF=22-15=1,
故答案为:1.
本题考查了平行四边形的性质及图形的翻折问题,折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变.
11、x+5y=1 x﹣y=1
【解析】
通过十字相乘法,把方程左边因式分解,即可求解.
【详解】
∵x2+4xy﹣5y2=1,
∴(x+5y)(x﹣y)=1,
∴x+5y=1或x﹣y=1,
故答案为:x+5y=1和 x﹣y=1.
该题重点考查了因式分解中的十字相乘法,能顺利的把方程左边因式分解是解题的关键所在.十字相乘法相关的知识点是:必须是二次三项式,并且符合拆解的原则,即可利用十字相乘分解因式.
12、1
【解析】
根据根与系数的关系可得:α+β=2019,αβ=1,将其代入(α﹣2019)(β﹣2019)=αβ-2019(α+β)+ 中即可求出结论.
【详解】
∵α、β是一元二次方程x2﹣2019x+1=0的两实根,
∴α+β=2019,αβ=1,
∴(α﹣2019)(β﹣2019)=αβ-2019(α+β)+=1.
故答案为1.
本题考查了一元二次方程根与系数的关系,熟练运用一元二次方程根与系数的关系是解决问题的关键.
13、35°
【解析】
根据折叠的性质可得∠ECB=∠ECF,CB=CF,根据菱形的性质可得CB=CD,∠B=∠D=70°,∠BCD=180°-∠D=110°,求出等腰三角形DCF的顶角∠DCF,即可求出∠ECF的度数
【详解】
解:在菱形ABCD中,CB=CD,∠B=∠D=70°,∠BCD=180°-∠D=110°,
根据折叠可得:∠ECB=∠ECF,CB=CF,
∴CF=CD
∴∠DCF=180°-70°-70°=40°,
∴∠ECF=(∠BCD-∠DCF)=35°.
故答案为35°.
本题考查图形的翻折变换,关键是掌握折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.
三、解答题(本大题共5个小题,共48分)
14、见解析.
【解析】
由垂直得到∠EAD=∠FCB=90°,根据AAS可证明Rt△AED≌Rt△CFB,得到AD=BC,根据平行四边形的判定判断即可.
【详解】
证明:∵AD//BC
∴∠ADE=∠CBF
∵AE⊥AD,CF⊥BC.
∴∠DAE=∠BCF=90°
在△ADE和△CBF中
∵∠DAE=∠BCF,∠ADE=∠CBF,AE=CF.
∴△ADE≌△CBF(AAS)
∴AD=BC
∵AD//BC
∴四边形ABCD是平行四边形.
本题考查了平行四边形的判定,平行线的性质,全等三角形的性质和判定等知识点的应用,关键是推出AD=BC.
15、(1)AA =1或3;(2)AA =时,重叠部分是菱形.
【解析】
(1)根据平移的性质,结合阴影部分是平行四边形,设AA′=x,AC与A′B′相交于点E,则A′D=4-x,△AA′E是等腰直角三角形,根据平行四边形的面积公式即可列出方程求解;
(2)设AC与CD交于点F,当四边形A′ECF是菱形时,有A′E=A′F,设AA′=x,则A′E=x,A′D=4-x,再由A′F=A′D,可得方程,解之即得结果.
【详解】
(1)设AA′=x,AC与A′B′相交于点E,如图,
∵△ACD是正方形ABCD剪开得到的,
∴△ACD是等腰直角三角形,
∴∠A=45°,
∴△AA′E是等腰直角三角形,
∴A′E=AA′=x,A′D=AD-AA′=4-x,
∵阴影部分面积为3,
∴x(4-x)=3,
整理得,x2-4x+3=0,
解得x1=1,x2=3,
即移动的距离AA′=1或3.
(2)设AC与CD交于点F,当四边形A′ECF是菱形时,A′E=A′F,
设AA′=x,则A′E=CF=x,A′D=DF=4-x,
∵△A′DF是等腰直角三角形,
∴A′F=A′D,
即,
解得,
即当移动的距离为时,重叠部分是菱形.
本题考查了平移的性质、等腰直角三角形的性质和判定、正方形和菱形的性质及一元二次方程的解法等知识,解决本题的关键是抓住平移后图形的特点,利用方程思想解题.
16、答案不唯一,具体见解析
【解析】
解:
或
或
或
17、(1)见解析;(2)
【解析】
(1)首先通过角平分线的定义和平行四边形的性质,平行线的性质得出,则有,再利用一组邻边相等的平行四边形是菱形即可证明;
(2)首先根据题意和菱形的性质证明四边形OCPD是矩形,然后利用矩形的性质和勾股定理即可得出答案.
【详解】
(1)∵AC平分∠BAD,
.
∵四边形ABCD是平行四边形,
,
,
,
,
∴平行四边形ABCD是菱形;
(2)∵平行四边形ABCD是菱形,
∴,
.
∵DPAC,CPBD,
∴四边形OCPD是平行四边形.
,
∴四边形OCPD是矩形,
∴ .
本题主要考查四边形,掌握矩形,菱形的判定及性质和勾股定理是解题的关键.
18、问题背景:EF=BE+DF,理由见解析;探索延伸:结论仍然成立,理由见解析;实际应用:210海里.
【解析】
问题背景:延长FD到点G.使DG=BE.连结AG,即可证明△ABE≌△ADG,可得AE=AG,再证明△AEF≌△AGF,可得EF=FG,即可解题;
探索延伸:延长FD到点G.使DG=BE.连结AG,即可证明△ABE≌△ADG,可得AE=AG,再证明△AEF≌△AGF,可得EF=FG,即可解题;
实际应用:连接EF,延长AE、BF相交于点C,然后与(2)同理可证.
【详解】
问题背景:EF=BE+DF,证明如下:
在△ABE和△ADG中,
,
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG,
∵∠EAF=∠BAD,
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=∠EAF,
∴∠EAF=∠GAF,
在△AEF和△GAF中,
,
∴△AEF≌△AGF(SAS),
∴EF=FG,
∵FG=DG+DF=BE+DF,
∴EF=BE+DF,
故答案为 EF=BE+DF;
探索延伸:结论EF=BE+DF仍然成立,
理由:延长FD到点G.使DG=BE,连结AG,如图2,
在△ABE和△ADG中,,
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG,
∵∠EAF=∠BAD,
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=∠EAF,
∴∠EAF=∠GAF,
在△AEF和△GAF中,
,
∴△AEF≌△AGF(SAS),
∴EF=FG,
∵FG=DG+DF=BE+DF,
∴EF=BE+DF;
实际应用:如图3,连接EF,延长AE、BF相交于点C,
∵∠AOB=30°+90°+(90°-70°)=140°,∠EOF=70°,
∴∠EOF=∠AOB,
又∵OA=OB,∠OAC+∠OBC=(90°-30°)+(70°+50°)=180°,
∴符合探索延伸中的条件,
∴结论EF=AE+BF成立,
即EF=2×(45+75)=260(海里),
答:此时两舰艇之间的距离是260海里.
本题考查了全等三角形的判定以及全等三角形对应边相等的性质,本题中求证△AEF≌△AGF是解题的关键.
一、填空题(本大题共5个小题,每小题4分,共20分)
19、10
【解析】
连接AD,根据等腰三角形的性质可得而AD⊥BC,根据三角形的面积求出AD的长,由EF是AC的垂直平分线可得当AD,EF交点M时,周长的最小值为AD+CD的长,故可求解.
【详解】
连接AD,∵,点为边的中点,
∴AD⊥BC,
∵,的面积是,
∴AD=16×2÷4=8,
∵EF是AC的垂直平分线,
∴点C关于直线EF的对称点为A,
∴AD的长为CM+MD的最小值,
∴周长的最小值为AD+CD=8+BC=8+2=10.
故填:10.
此题主要考查对称轴的应用,解题的关键是熟知等腰三角形的性质及垂直平分线的性质.
20、
【解析】
由得到再代入所求的代数式进行计算.
【详解】
∵,
∴,
∴,
故答案为:.
此题考查分式的求值计算,根据已知条件求出m与n的等量关系是解题的关键.
21、70
【解析】
首先由旋转的性质,得△ABC≌△A′B′C,然后利用等腰直角三角形的性质等角转换,即可得解.
【详解】
由旋转的性质,得△ABC≌△A′B′C,
∴AC=A′C,∠BAC=∠B′A′C,∠ACA′=90°,
∴∠CAA′=∠CA′A=45°
∵
∴∠BAC=25°
∴∠BAA′=∠BAC+∠CAA′=25°+45°=70°
故答案为:70.
此题主要考查利用全等三角形旋转求解角度,熟练掌握,即可解题.
22、m(m﹣9)
【解析】
直接提取公因式m即可.
【详解】
解:原式=m(m﹣9).
故答案为:m(m﹣9)
此题主要考查了提公因式法分解因式,关键是正确找出公因式.
23、6厘米
【解析】
根据直角三角形斜边中线等于斜边一半算出AB,再根据中位线的性质求出EF即可.
【详解】
∵∠BCA=90°,且D是AB的中点,CD=6,
∴AB=2CD=12,
∵E、F是AC、BC的中点,
∴EF=.
故答案为:6厘米
本题考查直角三角形中线的性质、中位线的性质,关键在于熟练掌握相关基础知识.
二、解答题(本大题共3个小题,共30分)
24、.
【解析】
根据分式的混合运算法则进行运算,最后化成最简分式即可.
【详解】
,
=,
=
=.
此题主要考查了分式的加减运算,分工的化简等知识点的理解和掌握,能熟练地进行有关分式的运算是解此题的关键.
25、2400元
【解析】
试题分析:连接AC,根据勾股定理求出AC,根据勾股定理的逆定理求出∠ACB=90°,求出区域的面积,即可求出答案.
试题解析:连结AC,
在Rt△ACD中,∠ADC=90°,AD=4米,CD=3米,由勾股定理得:AC=(米),
∵AC2+BC2=52+122=169,AB2=132=169,∴AC2+BC2=AB2,∴∠ACB=90°,
该区域面积S=S△ACB﹣S△ADC=×5×12﹣×3×4=24(平方米),
即铺满这块空地共需花费=24×100=2400元.
考点:1.勾股定理;2.勾股定理的逆定理.
26、1
【解析】
由题设知a≥3,化简原式得,根据非负数的性质先求出a,b的值,从而求得a+b的值.
【详解】
解:∵a≥3,
∴原等式可化为,
∴b+2=0且(a-3)b2=0,
∴a=3,b=-2,
∴a+b=1.
本题考查了二次根式有意义的条件及非负数的性质,几个非负数的和为零,则每一个数都为零.
题号
一
二
三
四
五
总分
得分
常德市重点中学2025届数学九年级第一学期开学学业水平测试试题【含答案】: 这是一份常德市重点中学2025届数学九年级第一学期开学学业水平测试试题【含答案】,共17页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
安庆市重点中学2025届九年级数学第一学期开学学业水平测试模拟试题【含答案】: 这是一份安庆市重点中学2025届九年级数学第一学期开学学业水平测试模拟试题【含答案】,共21页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2025届淮北市重点中学九年级数学第一学期开学学业水平测试试题【含答案】: 这是一份2025届淮北市重点中学九年级数学第一学期开学学业水平测试试题【含答案】,共18页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












