北京市第八中学2024-2025学年九上数学开学统考模拟试题【含答案】

这是一份北京市第八中学2024-2025学年九上数学开学统考模拟试题【含答案】，共29页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）等腰三角形的底边和腰长分别是10和12，则底边上的高是（ ）
A．13B．8C．D．
2、（4分）已知三角形的三边为2、3、4，该三角形的面积为( )
A．B．C．D．
3、（4分）如图所示,在▱ABCD中,分别以AB,AD为边向外作等边△ABE,△ADF,延长CB交AE于点G,点G在点A,E之间,连接CG,CF,则下列结论不一定正确的是( )
A．△CDF≌△EBC
B．∠CDF=∠EAF
C．CG⊥AE
D．△ECF是等边三角形
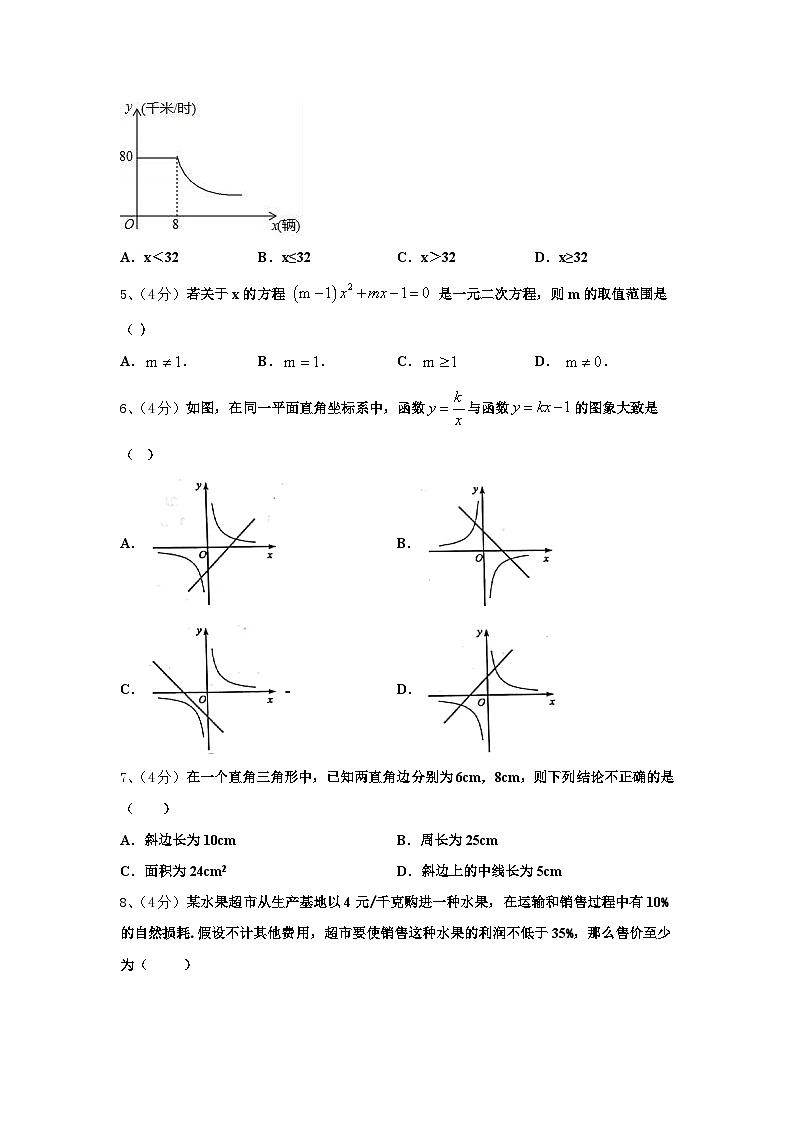
4、（4分）随着私家车的增加，交通也越来越拥挤，通常情况下，某段公路上车辆的行驶速度（千米/时）与路上每百米拥有车的数量x（辆）的关系如图所示，当x≥8时，y与x成反比例函数关系，当车速度低于20千米/时，交通就会拥堵，为避免出现交通拥堵，公路上每百米拥有车的数量x应该满足的范围是（ ）
A．x＜32B．x≤32C．x＞32D．x≥32
5、（4分）若关于x的方程 是一元二次方程，则m的取值范围是（ ）
A．.B．.C．D．.
6、（4分）如图，在同一平面直角坐标系中，函数与函数的图象大致是（ ）
A．B．
C．D．
7、（4分）在一个直角三角形中，已知两直角边分别为6cm，8cm，则下列结论不正确的是（ ）
A．斜边长为10cmB．周长为25cm
C．面积为24cm2D．斜边上的中线长为5cm
8、（4分）某水果超市从生产基地以4元/千克购进一种水果，在运输和销售过程中有10%的自然损耗.假设不计其他费用，超市要使销售这种水果的利润不低于35%，那么售价至少为（ ）
A．5.5元/千克B．5.4元/千克C．6.2元/千克D．6元/千克
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）对于实数c，d，min{c，d}表示c，d两数中较小的数，如min{3，﹣1}＝﹣1．若关于x的函数y＝min{2x2，a(x﹣t)2}(x≠0)的图象关于直线x＝3对称，则a的取值范围是_____，对应的t值是______．
10、（4分）如图，在△ABC中，∠A＝m°，∠ABC和∠ACD的平分线交于点A1，得∠A1；∠A1BC和∠A1CD的平分线交于点A2，得∠A2；…∠A2018BC和∠A2018CD的平分线交于点A2019，得∠A2019，则∠A2019＝_____°．
11、（4分）如图，在矩形ABCD中，∠BAD的平分线交BC于点E，交DC的延长线于点F，点G是EF的中点，连接CG、BG、BD、DG，下列结论：① BC=DF，②∠DGF=135；③BG⊥DG，④ 若3AD=4AB，则4S△BDG=25S△DGF；正确的是____________（只填番号）．
12、（4分）如图，在菱形ABCD 中，AC与BD相交于点O，点P是AB的中点，PO＝2，则菱形ABCD的周长是_________.
13、（4分）将5个边长为1的正方形按照如图所示方式摆放，O1，O2，O3，O4，O5是正方形对角线的交点，那么阴影部分面积之和等于________．
三、解答题（本大题共5个小题，共48分）
14、（12分）如图，一架5米长的梯子AB斜靠在一面墙上，梯子底端B到墙底的垂直距离BC为3米．
（1）求这个梯子的顶端A到地面的距离AC的值；
（2）如果梯子的顶端A沿墙AC竖直下滑1米到点D处，求梯子的底端B在水平方向滑动了多少米？
15、（8分）已知，直线与双曲线交于点，点.
（1）求反比例函数的表达式；
（2）根据图象直接写出不等式的解集 .
（3）将直线沿轴向下平移后，分别与轴，轴交于点，点，当四边形为平行四边形时，求直线的表达式.
16、（8分）计算（+1）（-1）+÷−.
17、（10分）如图，四边形ABCD是正方形，点E是BC边上的点，∠AEF=90°，且EF交正方形外角的平分线CF于点F．
（1）如图①，当点E是BC边上任一点（不与点B、C重合）时，求证：AE=EF．
（2）如图②当点E是BC边的延长线上一点时，（1）中的结论还成立吗？ （填成立或者不成立）．
（3）当点E是BC边上任一点（不与点B、C重合）时，若已知AE=EF，那么∠AEF的度数是否发生变化？证明你的结论．
18、（10分）如图，方格纸中每个小正方形的边长都是1个单位长度，的三个顶点，，．
(1)将以点为旋转中心旋转，得到△，请画出△的图形；
(2)平移，使点的对应点坐标为，请画出平移后对应的△的图形；
(3)若将△绕某一点旋转可得到△，请直接写出旋转中心的坐标．
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）如图，P是反比例函数图象上的一点，轴于A，点B，C在y轴上，四边形PABC是平行四边形，则▱PABC的面积是______．
20、（4分）如图，在□ABCD中，对角线AC、BD相交于点O，AB=OB，E为AC上一点，BE平分∠ABO，EF⊥BC于点F，∠CAD=45°，EF交BD于点P，BP=，则BC的长为_______．
21、（4分）如图，在正方形中，点是对角线上一点，连接，将绕点逆时针方向旋转到，连接，交于点，若，，则线段的长为___________．
22、（4分）若方程x2﹣x＝0的两根为x1，x2(x1＜x2)，则x2﹣x1＝______．
23、（4分）如图，在□ABCD中，对角线AC和BD交于点O，点E为AB边上的中点，OE=2.5cm，则AD=________cm。
二、解答题（本大题共3个小题，共30分）
24、（8分）如图，一架长的梯子斜靠在一竖直的墙上，，这时.如果梯子的顶端沿墙下滑，那么梯子底端也外移吗？
25、（10分）如图，在▱ABCD中，AC、BD交于点O，BD⊥AD于点D，将△ABD沿BD翻折得到△EBD，连接EC、EB．
（1）求证：四边形DBCE是矩形；
（2）若BD=4，AD=3，求点O到AB的距离．
26、（12分）已知，如图，E、F分别为□ABCD的边BC、AD上的点，且∠1=∠2,.求证：AE=CF.
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、D
【解析】
先作底边上的高，由等腰三角形的性质和勾股定理即可求出此高的长度．
【详解】
解：作底边上的高并设此高的长度为x，
由等腰三角形三线合一的性质可得高线平分底边，
根据勾股定理得：52+x2=122，
解得x=
本题考点：等腰三角形底边上高的性质和勾股定理，等腰三角形底边上的高所在直线为底边的中垂线．然后根据勾股定理即可求出底边上高的长度．
2、D
【解析】
如图所示：过点B作BD⊥AC于点D，利用勾股定理得出BD的长，进而利用三角形面积求法得出答案．
【详解】
如图所示：过点B作BD⊥AC于点D，
设BD=x，CD=y，
则AD=4-y，
在Rt△BDC中，x2+y2=32，
在Rt△ABD中，x2+（4-y）2=22，
故9+16-8y=4，解得：y= ，
∴x2+（）2=9，解得：x=
故三角形的面积为：
故选：D．
本题考查勾股定理的应用，根据题意得出三角形的高的值是解题关键．
3、C
【解析】
A.在平行四边形ABCD中，∠ADC=∠ABC，AD=BC，CD=AB，
∵△ABE、△ADF都是等边三角形，
∴AD=DF，AB=EB，∠ADF=∠ABE=60°，
∴DF=BC，CD=BC，
∴∠CDF=360°-∠ADC-60°=300°-∠ADC，
∠EBC=360°-∠ABC-60°=300°-∠ABC，
∴∠CDF=∠EBC，
在△CDF和△EBC中，
DF=BC,
∠CDF=∠EBC,
CD=EB,
∴△CDF≌△EBC（SAS），故A正确；
B.在平行四边形ABCD中，∠DAB=180°-∠ADC，
∴∠EAF=∠DAB+∠DAF+∠BAE=180°-∠ADC+60°+60°=300°-∠ADC，
∴∠CDF=∠EAF，故B正确；
C. .当CG⊥AE时，∵△ABE是等边三角形，
∴∠ABG=30°，
∴∠ABC=180°-30°=150°，
∵∠ABC=150°无法求出，故C错误；
D. 同理可证△CDF≌△EAF，
∴EF=CF，
∵△CDF≌△EBC，
∴CE=CF，
∴EC=CF=EF，
∴△ECF是等边三角形，故D正确；
故选C.
点睛：本题考查了全等三角形的判定、等边三角形的判定和性质、平行四边形的性质等知识，综合性强．考查学生综合运用数学知识的能力．根据题意，结合图形，对选项一一求证，判定正确选项．
4、B
【解析】
利用已知反比例函数图象过（8，80），得出其函数解析式，再利用y=20时，求出x的最值，进而求出x的取值范围．
【详解】
解：设反比例函数的解析式为：，
则将（8，80），代入,得：k=xy=8×80=640，
∴反比例函数的解析式为：
故当车速度为20千米/时，则，
解得：x=1，
故高架桥上每百米拥有车的数量x应该满足的范围是：0故答案为x≤1．
此题主要考查了反比例函数的应用，根据题意得出函数解析式是解题关键．
5、A
【解析】
根据一元二次方程的定义可得m﹣1≠0，再解即可．
【详解】
由题意得：m﹣1≠0，
解得：m≠1，
故选A．
此题主要考查了一元二次方程的定义，关键是掌握只含有一个未知数，并且未知数的最高次数是2的整式方程叫一元二次方程．
6、A
【解析】
分情况讨论：和时，根据图像的性质，即可判定.
【详解】
当时，函数的图像位于第一、三象限，函数的图像第一、三、四象限；
当时，函数的图像位于第二、四象限，函数的图像第二、三、四象限；
故答案为A.
此题主要考查一次函数和反比例函数的性质，熟练掌握，即可解题.
7、B
【解析】
试题解析：∵在一个直角三角形中，已知两直角边分别为6cm，8cm，
∴直角三角形的面积=×6×8=24cm2，故选项C不符合题意；
∴斜边 故选项A不符合题意；
∴斜边上的中线长为5cm，故选项D不符合题意；
∵三边长分别为6cm，8cm，10cm，
∴三角形的周长=24cm，故选项B符合题意，
故选B．
点睛：直角三角形斜边的中线等于斜边的一半.
8、D
【解析】
设这种水果每千克的售价为x元，购进这批水果m千克，根据这种水果的利润不低于35%列不等式求解即可.
【详解】
设这种水果每千克的售价为x元，购进这批水果m千克，根据题意，得
(1-10%)mx-4m≥4m×35%，
解得x≥6，
答：售价至少为6元/千克.
故选D.
此题主要考查了一元一次不等式的应用，根据实际问题中的条件列不等式时，要注意抓住题目中的一些关键性词语，找出不等关系，列出不等式式是解题关键．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、a＝2或a＜0 6或2
【解析】
可令y1=2x2，y2=a（x-t）2可分两种情况：①当y1与y2关于x=2对称时，可求出相应的a值为2，t值为6；②由于y1=2x2恒大于零，此时若y2恒小于零时，a<0，可得y2对称轴为x=2，即可求出相应的t值．
【详解】
解：设y1＝2x2，y2＝a(x﹣t)2
①当y1与y2关于x＝2对称时，可得a＝2，t＝6
②在y＝min{y1，y2}(x≠0)中，y1与y2没重合部分，即无论x为何值，y＝y2
即y2恒小于等于y1，那么由于y对x＝2对称，也即y2对于x＝2对称，得a＜0，t＝2．
综上所述，a＝2或a＜0，对应的t值为6或2
故答案为：a＝2或a＜0，6或2
本题考查的是二次函数的图象与几何变换，先根据题意求出a的值是解答此题的关键.
10、
【解析】
根据角平分线的定义可得∠A1BC=∠ABC，∠A1CD=∠ACD，再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ACD=∠A+∠ABC，∠A1CD=∠A1+∠A1BC，然后整理得到∠A1=∠A；
【详解】
∵∠ABC与∠ACD的平分线交于点A1，
∴∠A1BC=∠ABC，∠A1CD=∠ACD，
由三角形的外角性质，∠ACD=∠A+∠ABC，
∠A1CD=∠A1+∠A1BC，（∠A+∠ABC）=∠A1+∠A1BC=∠A1+∠ABC，
整理得，∠A1=∠A=×m°=°；
同理可得∠An=()n×m,
所以∠A2019＝()2019×m＝.
故答案是：．
考查了三角形的内角和定理，三角形的一个外角等于与它不相邻的两个内角的和的性质，角平分线的定义，熟记性质与定义并求出后一个角是前一个角的是解题的关键．
11、①③④
【解析】
根据矩形的性质得：BC=AD，∠BAD=∠ADC=90°，由角平分线可得△ADF是等腰直角三角形，则BC=DF=AD，故①正确；
先求出∠BAE=45°，判断出△ABE是等腰直角三角形，根据等腰直角三角形的性质可得AB=BE，∠AEB=45°，从而得到BE=CD；再求出△CEF是等腰直角三角形，根据等腰直角三角形的性质可得CG=EG，再求出∠BEG=∠DCG=135°，然后利用“边角边”证明△BEG≌△DCG，得到∠BGE=∠DGC，由∠BGE＜∠AEB，得到∠DGC=∠BGE＜45°，∠DGF＜135°，故②错误；
由全等三角形的性质可得∠BGE=∠DGC，即可得到③正确；
由△BGD是等腰直角三角形得到BD=5a，求得S△BDG，过G作GM⊥CF于M，求得S△DGF，进而得出答案．
【详解】
∵四边形ABCD是矩形，∴BC=AD，∠BAD=∠ADC=90°．
∵AF平分∠BAD，∴∠BAE=∠DAF=45°，∴△ADF是等腰直角三角形，∴DF=AD，∴BC=DF，故选项①正确；
∵AE平分∠BAD，∴∠BAE=45°，∴△ABE是等腰直角三角形，∴AB=BE，∠AEB=45°．
∵AB=CD，∴BE=CD；
∵∠CEF=∠AEB=45°，∠ECF=90°，∴△CEF是等腰直角三角形．
∵点G为EF的中点，∴CG=EG，∠FCG=45°，∴∠BEG=∠DCG=135°．
在△BEG和△DCG中，∵，∴△BEG≌△DCG（SAS），∴∠BGE=∠DGC．
∵∠BGE＜∠AEB，∴∠DGC=∠BGE＜45°．
∵∠CGF=90°，∴∠DGF＜135°，故②错误；
∵△BEG≌△DCG，∴∠BGE=∠DGC，BG=DG．
∵∠EGC=90°，∴∠BGD=90°，∴BG⊥DG，故③正确；
∵3AD=4AB，∴，∴设AB=3a，则AD=4a．
∵BD=5a，∴BG=DGa，∴S△BDGa1．
过G作GM⊥CF于M．
∵CE=CF=BC﹣BE=BC﹣AB=a，∴GMCFa，∴S△DGF•DF•GM4aa=a1，∴S△BDGS△DGF，∴4S△BDG=15S△DGF，故④正确．
故答案为①③④．
本题考查了矩形的性质、全等三角形的判定与性质、等腰直角三角形的判定与性质；熟练掌握矩形的性质，证明三角形全等和等腰直角三角形是解决问题的关键．
12、1
【解析】
根据菱形的性质可得AC⊥BD，AB=BC=CD=AD，再根据直角三角形的性质可得AB=2OP，进而得到AB长，然后可算出菱形ABCD的周长．
【详解】
∵四边形ABCD是菱形，
∴AC⊥BD，AB=BC=CD=AD，
∵点P是AB的中点，
∴AB=2OP，
∵PO=2，
∴AB=4，
∴菱形ABCD的周长是：4×4=1，
故答案为：1．
此题主要考查了菱形的性质，关键是掌握菱形的两条对角线互相垂直，四边相等，此题难度不大．
13、1 .
【解析】
分析：连接O1A,O1B，先证明△AO1C≌△BO1D，从而可得S四边形ACO1D=S△AO1B=S正方形ABEF=,然后可求阴影部分面积之和.
详解：如图，连接O1A,O1B.
∵四边形ABEF是正方形，
∴O1A=O1B, ∠AO1B=90°.
∵∠AO1C+∠AO1D=90°, ∠BO1D+∠AO1D=90°,
∴∠AO1C=∠BO1D.
在△AO1C和△BO1D中，
∵∠AO1C=∠BO1D，
O1A=O1B,
∠O1AC=∠O1BD=45°,
∴△AO1C≌△BO1D，
∴S四边形ACO1D=S△AO1B=S正方形ABEF=,
∴阴影部分面积之和等于×4=1.
故答案为：1.
点睛：本题考查了正方形的性质，全等三角形的判定与性质，证明△AO1C≌△BO1D是解答本题的关键.
三、解答题（本大题共5个小题，共48分）
14、（1）4（2）1
【解析】
（1）在直角三角形ABC中，利用勾股定理即可求出AC的长；
（2）首先求出CD的长，利用勾股定理可求出CE的长，进而得到BE=CE-CB的值．
【详解】
（1）在Rt△ABC中，由勾股定理得AC2+CB2=AB2，
即AC2+32=52，
所以AC=4（m），
即这个梯子的顶端A到地面的距离AC为4m；
（2）DC=4-1=3（m），DE=5=m，
在Rt△DCE中，由勾股定理得DC2+CE2=DE2，
即32+CE2=52，
所以CE=5（m），
BE=CE-CB=4-3=1（m），
即梯子的底端B在水平方向滑动了1m．
本题考查了勾股定理在实际生活中的应用，本题中根据梯子长不会变这一关系进行求解是解题的关键．
15、（1）；（2）或；（3）,
【解析】
（1）将点A代入直线解析式即可得出其坐标，再代入反比例函数解析式，即可得解；
（2）首先联立两个函数，解得即可得出点B坐标，直接观察图像，即可得出解集；
（3）首先过点作轴，过点作轴，交于点，根据平行线的性质，得出，得出，进而得出直线CD解析式.
【详解】
解：（1）根据题意，可得点
将其代入反比例函数解析式，即得
（2）根据题意，得
解得
∴点B（4，-2）
∴直接观察图像，可得的解集为
或
（3）过点作轴，过点作轴，交于点
根据题意，可得
∴∠EAB=∠NOB=∠OCD，∠AEB=∠COD=90°，AB=CD
∴∠ABE=∠CDO
∴（ASA）
∴
则可得出直线CD为
此题主要考查一次函数、反比例函数和平行四边形的综合应用，熟练运用，即可解题.
16、1+
【解析】
根据实数的运算法则求解.
【详解】
解：原式=2-1+-
=1+
本题考查了实数的运算,属于简单题,熟悉实数运算法则是解题关键.
17、（1）见解析；（2）成立，理由见解析；（3）∠AEF=90°不发生变化．理由见解析.
【解析】
（1）在AB上取点G，使得BG=BE，连接EG，根据已知条件利用ASA判定△AGE≌△ECF，因为全等三角形的对应边相等，所以AE=EF；
（2）在BA的延长线上取一点G，使AG=CE，连接EG，根据已知利用ASA判定△AGE≌△ECF，因为全等三角形的对应边相等，所以AE=EF；
（3）在BA边取一点G，使BG=BE，连接EG．作AP⊥EG，EQ⊥FC，先证AGP≌△ECQ得AP=EQ，再证Rt△AEP≌Rt△EFQ得∠AEP=∠EFQ，∠BAE=∠CEF，结合∠AEB+∠BAE=90°知∠AEB+∠CEF=90°，从而得出答案．
【详解】
（1）证明：在BA边取一点G，使BG=BE，连接EG，
∵四边形ABCD是正方形，
∴∠B=90°，BA=BC，∠DCM═90°，
∴BA-BG=BC-BE，
即 AG=CE．
∵∠AEF=90°，∠B=90°，
∴∠AEB+∠CEF=90°，∠AEB+∠BAE=90°，
∴∠CEF=∠BAE．
∵BG=BE，CF平分∠DCM，
∴∠BGE=∠FCM=45°，
∴∠AGE=∠ECF=135°，
∴△AGE≌△ECF（ASA），
∴AE=EF．
（2）成立，
理由：在BA的延长线上取点G，使得AG=CE，连接EG．
∵四边形ABCD为正方形，AG=CE，
∴∠B=90°，BG=BE，
∴△BEG为等腰直角三角形，
∴∠G=45°，
又∵CF为正方形的外角平分线，
∴∠ECF=45°，
∴∠G=∠ECF=45°，
∵∠AEF=90°，
∴∠FEM=90°-∠AEB，
又∵∠BAE=90°-∠AEB，
∴∠FEM=∠BAE，
∴∠GAE=∠CEF，
在△AGE和△ECF中，
∵，
∴△AGE≌△ECF（ASA），
∴AE=EF．
故答案为：成立．
（3）∠AEF=90°不发生变化．
理由如下：在BA边取一点G，使BG=BE，连接EG．分别过点A、E作AP⊥EG，EQ⊥FC，垂足分别为点P、Q，
∴∠APG=∠EQC=90°，
由（1）中知，AG=CE，∠AGE=∠ECF=135°，
∴∠AGP=∠ECQ=45°，
∴△AGP≌△ECQ（AAS），
∴AP=EQ，
∴Rt△AEP≌Rt△EFQ（HL），
∴∠AEP=∠EFQ，
∴∠BAE=∠CEF，
又∵∠AEB+∠BAE=90°，
∴∠AEB+∠CEF=90°，
∴∠AEF=90°．
此题是四边形综合题，主要考查的是正方形的性质、全等三角形的判定和性质，正确作出辅助线、灵活运用全等三角形的判定定理和性质定理是解题的关键，解答时，注意类比思想的正确运用．
18、 (1)见解析；(2)见解析；(3)旋转中心坐标．
【解析】
（1）利用旋转的性质得出对应点坐标进而得出答案；
（2）利用平移规律得出对应点位置，进而得出答案；
（3）利用旋转图形的性质，连接对应点，即可得出旋转中心的坐标.
【详解】
（1）如图所示，即为所求；
（2）如图所示，即为所求；
（3）旋转中心坐标.
此题主要考查了旋转的性质以及图形的平移等知识，根据题意得出对应点坐标是解题关键.
一、填空题（本大题共5个小题，每小题4分，共20分）
19、6
【解析】
作PD⊥BC,所以，设P（x，y）. 由，得平行四边形面积=BC•PD=xy.
【详解】
作PD⊥BC,
所以，设P（x，y）.
由，
得平行四边形面积=BC•PD=xy=6.
故答案为：6
本题考核知识点：反比例函数意义. 解题关键点：熟记反比例函数的意义.
20、1
【解析】
过点E作EM∥AD，由△ABO是等腰三角形，根据三线合一可知点E是AO的中点，可证得EM=AD=BC，根据已知可求得∠CEF=∠ECF=15°，从而得∠BEF=15°，△BEF为等腰直角三角形，可得BF=EF=FC=BC，因此可证明△BFP≌△MEP（AAS），则EP=FP=FC，在Rt△BFP中，利用勾股定理可求得x，即得答案．
【详解】
过点E作EM∥AD，交BD于M，设EM=x，
∵AB=OB，BE平分∠ABO，
∴△ABO是等腰三角形，点E是AO的中点，BE⊥AO，∠BEO=90°，
∴EM是△AOD的中位线，
又∵ABCD是平行四边形，
∴BC=AD=2EM=2x，
∵EF⊥BC， ∠CAD=15°，AD∥BC，
∴∠BCA=∠CAD=15°，∠EFC=90°，
∴△EFC为等腰直角三角形，
∴EF=FC，∠FEC=15°，
∴∠BEF=90°-∠FEC=15°，
则△BEF为等腰直角三角形，
∴BF=EF=FC=BC=x，
∵EM∥BF，
∴∠EMP=∠FBP，∠PEM=∠PFB=90°，EM=BF，
则△BFP≌△MEP（ASA），
∴EP=FP=EF=FC=x，
∴在Rt△BFP中，，
即：，
解得：，
∴BC=2=1，
故答案为：1．
考查了平行四边形的性质，等腰三角形的性质，三线合一的应用，平行线的性质，全等三角形的判定和性质，利用勾股定理求三角形边长，熟记图形的性质定理是解题的关键．
21、
【解析】
连接EF，过点E作EM⊥AD，垂足为M，设ME=HE=FH=x，则GH=3-x，从而可得到，于是可求得x的值，最后在Rt△AME中，依据勾股定理可求得AE的长．
【详解】
解：如图所示：连接EF，过点E作EM⊥AD，垂足为M．
∵ABCD为正方形，EM⊥AD，∠EDF=90°，AD=BC=CD=DG+CG=5，
∴△MED和△DEF均为等腰直角三角形．
∵DE=DF，∠EDH=∠FDH=45°，
∴DH⊥EF，EH=HF，
∴FH∥BC．
设ME=HE=FH=x，则GH=3﹣x．
由FH∥BC可知：，
即，解得：，
∴．
在Rt△AME中，．
故答案为：．
本题主要考查的是正方形的性质、等腰直角三角形的性质和判定、平行线分线段成比例定理、勾股定理的应用，求得ME的长是解题的关键．
22、1
【解析】
求出x1,x2即可解答.
【详解】
解：∵x2﹣x＝0，
∴x(x﹣1)＝0，
∵x1＜x2，
∴解得：x1＝0，x2＝1，
则x2﹣x1＝1﹣0＝1．
故答案为：1．
本题考查一元二次方程的根求解，按照固定过程求解即可，较为简单.
23、5
【解析】
由平行四边形的对角线互相平分得AO=OC，结合E为AB的中点，则OE为△ABC的中位线，得到BC=2OE，从而求出BC的长.
【详解】
∵四边形ABCD是平行四边形，
∴OA=OC，
又∵E为AB的中点，
∴OE为△ABC的中位线 ，
∴BC=2OE=2×2.5=5cm
故答案为：5.
此题主要考查中位线的性质，解题的关键是熟知中位线的判断与性质.
二、解答题（本大题共3个小题，共30分）
24、梯子的顶端沿墙下滑时，梯子底端并不是也外移，而是外移.
【解析】
先根据勾股定理求出OB的长，再根据梯子的长度不变求出OD的长，根据BD=OD-OB即可得出结论．
【详解】
解：∵在中，，，
∴.
∴
在中，，
∴.
∴
∴
∴梯子的顶端沿墙下滑时，梯子底端并不是也外移，
而是外移.
本题考查的是勾股定理的应用，在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法，关键是从题中抽象出勾股定理这一数学模型，画出准确的示意图．领会数形结合的思想的应用．
25、（1）见解析；（2）点O到AB的距离为．
【解析】
（1）先利用折叠的性质和平行四边形的性质得出DE∥BC，DE=BC，则四边形DBCE是平行四边形，再利用BE=CD即可证明四边形DBCE是矩形；
（2）过点O作OF⊥AB，垂足为F，先利用勾股定理求出AB的长度，然后利用 面积即可求出OF的长度，则答案可求．
【详解】
（1）由折叠性质可得：AD=DE，BA=BE，
∵四边形ABCD是平行四边形，
∴AD=BC，AD∥BC，BA=CD，
∴DE∥BC，DE=BC，
∴四边形DBCE是平行四边形，
又∵BE=CD，
∴四边形DBCE是矩形．
（2）过点O作OF⊥AB，垂足为F，
∵BD⊥AD，
∴∠ADB=90°，
在Rt△ADB中，BD=4，AD=3，
由勾股定理得：AB=，
又∵四边形ABCD是平行四边形，
∴OB=OD=，

∴
答：点O到AB的距离为．
本题主要考查平行四边形的性质，矩形的判定，勾股定理，掌握平行四边形的性质，矩形的判定，勾股定理并能够利用三角形面积进行转化是解题的关键．
26、详见解析
【解析】
通过证明三角形全等求得两线段相等即可.
【详解】
∵四边形ABCD为平行四边形
∴∠B=∠D，AB=CD
在△ABE与△CDF中，∠1=∠2，∠B=∠D，AB=CD
∴△ABE≌△CDF
∴AE=CF
本题主要考查平行四边形性质与全等三角形，解题关键在于找到全等三角形.
题号
一
二
三
四
五
总分
得分