安徽省芜湖市部分学校2024-2025学年数学九上开学达标测试试题【含答案】

这是一份安徽省芜湖市部分学校2024-2025学年数学九上开学达标测试试题【含答案】，共23页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
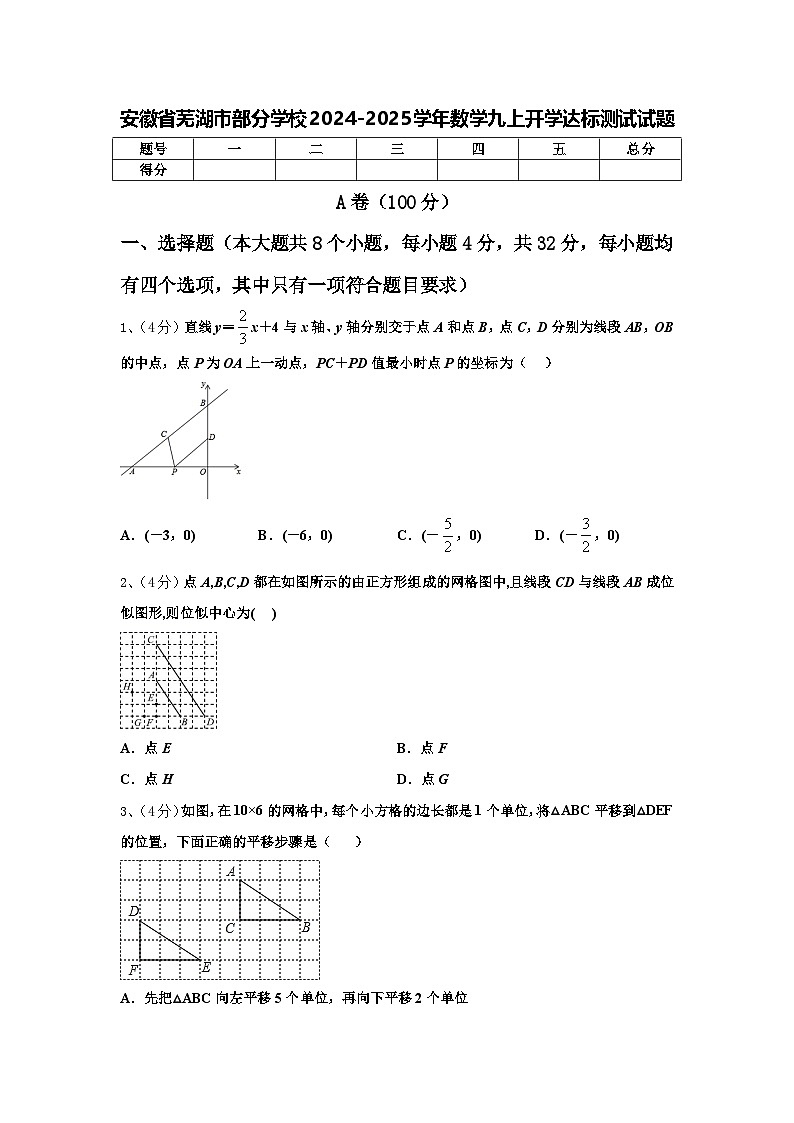
1、（4分）直线y＝x＋4与x轴、y轴分别交于点A和点B，点C，D分别为线段AB，OB的中点，点P为OA上一动点，PC＋PD值最小时点P的坐标为（ ）
A．(－3，0)B．(－6，0)C．(－，0)D．(－，0)
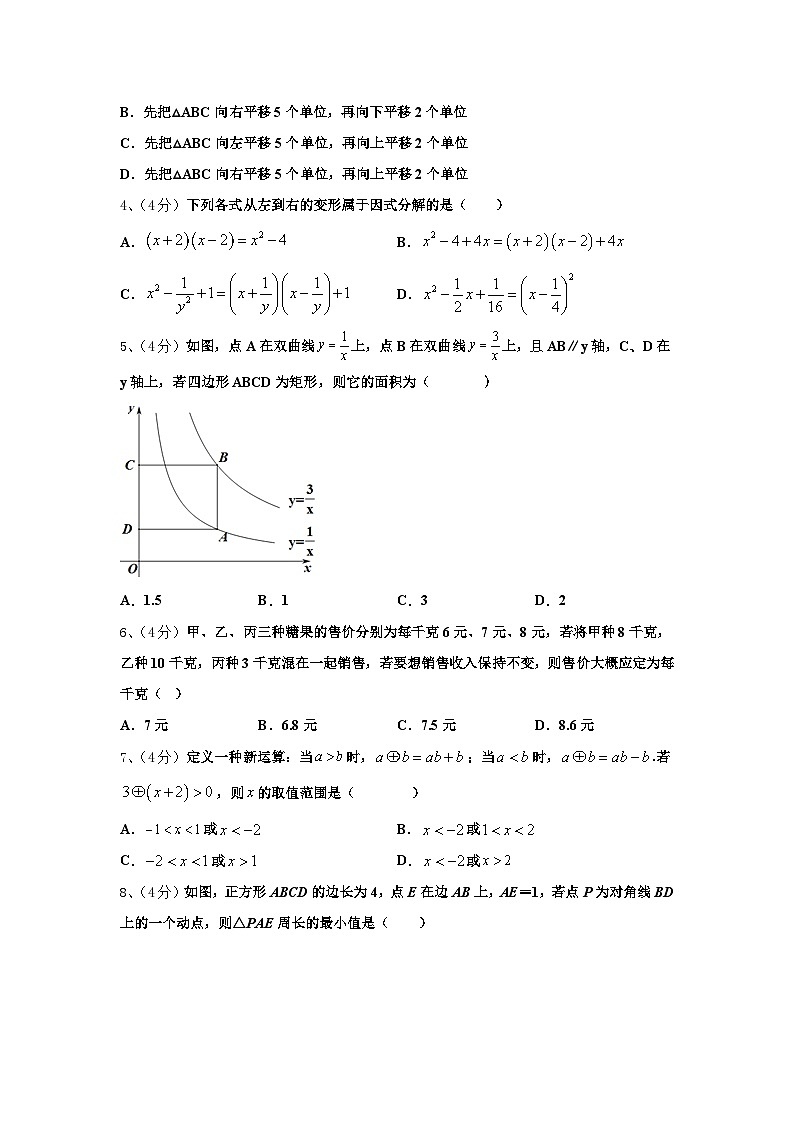
2、（4分）点A,B,C,D都在如图所示的由正方形组成的网格图中,且线段CD与线段AB成位似图形,则位似中心为( )
A．点EB．点F
C．点HD．点G
3、（4分）如图，在10×6的网格中，每个小方格的边长都是1个单位，将△ABC平移到△DEF的位置，下面正确的平移步骤是（ ）
A．先把△ABC向左平移5个单位，再向下平移2个单位
B．先把△ABC向右平移5个单位，再向下平移2个单位
C．先把△ABC向左平移5个单位，再向上平移2个单位
D．先把△ABC向右平移5个单位，再向上平移2个单位
4、（4分）下列各式从左到右的变形属于因式分解的是（ ）
A．B．
C．D．
5、（4分）如图，点A在双曲线上，点B在双曲线上，且AB∥y轴，C、D在y轴上，若四边形ABCD为矩形，则它的面积为（ ）
A．1.5B．1C．3D．2
6、（4分）甲、乙、丙三种糖果的售价分别为每千克6元、7元、8元，若将甲种8千克，乙种10千克，丙种3千克混在一起销售，若要想销售收入保持不变，则售价大概应定为每千克（ ）
A．7元B．6.8元C．7.5元D．8.6元
7、（4分）定义一种新运算：当时，；当时，.若，则的取值范围是（ ）
A．或B．或
C．或D．或
8、（4分）如图，正方形ABCD的边长为4，点E在边AB上，AE＝1，若点P为对角线BD上的一个动点，则△PAE周长的最小值是（ ）
A．3B．4C．5D．6
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）把直线向上平移2个单位得到的直线解析式为：_______.
10、（4分）如图，已知E是正方形ABCD的边AB上一点，点A关于DE的对称点为F，若正方形ABCD的边长为1，且∠BFC＝90°，则AE的长为___
11、（4分）如图，某校根据学生上学方式的一次抽样调查结果，绘制出一个未完成的扇形统计图，若该校共有学生1500人，则据此估计步行的有_____．
12、（4分）矩形（非正方形）四个内角的平分线围成的四边形是__________形.（埴特殊四边形）
13、（4分）20190=__________.
三、解答题（本大题共5个小题，共48分）
14、（12分）如图，是的中线，点是线段上一点(不与点重合).过点作，交于点，过点作，交的延长线于点，连接、.
(1)求证：；
(2)求证：；
(3)判断线段、的关系，并说明理由.
15、（8分）为贯彻落实关于“传承和弘扬中华优秀传统文化”的重要讲话精神，2018年5月27日我市举办了第二届湖南省青少年国学大赛永州复赛.本次比赛全市共有近200所学校4.6万名学生参加.经各校推荐报名、县区初赛选拔、市区淘汰赛的层层选拔，推选出优秀的学生参加全省的总决赛.下面是某县初赛时选手成绩的统计图表（部分信息未给出）.
请根据图表信息回答下列问题：
（1）在频数分布表中， ， .
（2）请将频数直方图补充完整；
（3）若测试成绩不低于120分为优秀，则本次测试的优秀率是多少？
16、（8分）小颖和同学一起去书店买书，他们先用60元买了一种科普书，又用60元买了一种文学书.科普书的价格比文学书高出一半，他们所买的科普书比所买的文学书少2本.
(1)求他们买的科普书和文学书的价格各是多少元？
(2)学校某月开展读书活动，班上同学让小颖帮助购买科普书和文学书共20本，且购买总费用不超过260元，求小颖至少购买多少本文学书？
17、（10分）解不等式组：，并把它的解集在数轴上表示出来．
18、（10分）为创建足球特色学校，营造足球文化氛围，某学校随机抽取部分八年级学生足球运球的测试成绩作为一个样本，按A，B，C，D四个等级进行统计，制成了如下不完整的统计图.（说明：A级：8分—10分，B级：7分—7.9分，C级：6分—6.9分，D级：1分—5.9分）根据所给信息，解答以下问题：
(1)样本容量为 ，C对应的扇形的圆心角是____度，补全条形统计图；
(2)所抽取学生的足球运球测试成绩的中位数会落在____等级；
(3)该校八年级有300名学生，请估计足球运球测试成绩达到级的学生有多少人？
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）如图，在矩形ABCD中，∠ABC的平分线交AD与点E，AB=2，BC=3，则CE=_____.
20、（4分）已知一个多边形的每一个外角都等于，则这个多边形的边数是 ．
21、（4分）若□ABCD中，∠A=50°，则∠C=_______°．
22、（4分）如图，△ABC中，已知M、N分别为AB、BC的中点，且MN＝3，则AC的长为_____．
23、（4分）已知反比例函数，若，且，则的取值范围是_____．
二、解答题（本大题共3个小题，共30分）
24、（8分）如图，DE⊥AB，CF⊥AB，垂足分别是点E、F，DE=CF，AE=BF，求证：AC∥BD．
25、（10分）已知：如图1，在平面直角坐标系中，直线与坐标轴分别相交于点，与直线相交于点.
（1）求点的坐标；
（2）若平行于轴的直线交于直线于点，交直线于点，交轴于点，且，求的值；
（3）如图2，点是第四象限内一点，且，连接，探究与之间的位置关系，并证明你的结论.
26、（12分）如图，在菱形ABCD中，AB=4cm，∠BAD=60°．动点E、F分别从点B、D同时出发，以1cm/s的速度向点A、C运动，连接AF、CE，取AF、CE的中点G、H，连接GE、FH．设运动的时间为ts（0＜t＜4）．
（1）求证：AF∥CE；
（2）当t为何值时，四边形EHFG为菱形；
（3）试探究：是否存在某个时刻t，使四边形EHFG为矩形，若存在，求出t的值，若不存在，请说明理由．
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、C
【解析】
作点D关于x轴的对称点D′，连接CD′交x轴于点P，此时PC+PD值最小，如图所示．
直线y=x+4与x轴、y轴的交点坐标为A（﹣6，0）和点B（0，4），
因点C、D分别为线段AB、OB的中点，可得点C（﹣3，1），点D（0，1）．
再由点D′和点D关于x轴对称，可知点D′的坐标为（0，﹣1）．
设直线CD′的解析式为y=kx+b，直线CD′过点C（﹣3，1），D′（0，﹣1），
所以，解得：，
即可得直线CD′的解析式为y=﹣x﹣1．
令y=﹣x﹣1中y=0，则0=﹣x﹣1，解得：x=﹣，
所以点P的坐标为（﹣，0）．故答案选C．
考点：一次函数图象上点的坐标特征；轴对称-最短路线问题．
2、B
【解析】
根据位似图形对应点连线过位似中心判断即可．
【详解】
解：点A、B、C、D都在如图所示的由正方形组成的网格图中，且线段CD与线段AB成位似图形，则位似中心为点F，
故选：B．
此题考查位似变换，解题关键是弄清位似中心的定义．
3、A
【解析】
解：根据网格结构，观察点对应点A、D，点A向左平移5个单位，再向下平移2个单位即可到达点D的位置，所以，平移步骤是：先把△ABC向左平移5个单位，再向下平移2个单位．
故选A．
4、D
【解析】
根据因式分解的定义依次判断各项即可解答.
【详解】
选项A，是整式的乘法运算，不是因式分解；
选项B，该等式右边没有化为几个整式的乘积形式，不是因式分解；
选项C，该等式右边没有化为几个整式的乘积形式，不是因式分解；
选项D，符合因式分解的定义，是因式分解.
故选D.
本题考查了因式分解的定义，熟练运用因式分解的定义是解决问题的关键.
5、D
【解析】
根据双曲线的图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的矩形的面积S的关系S=|k|即可判断．
【详解】
过A点作AE⊥y轴，垂足为E，
∵点A在双曲线y=上，
∴四边形AEOD的面积为1，
∵点B在双曲线y=上，且AB∥x轴，
∴四边形BEOC的面积为3，
∴四边形ABCD为矩形，则它的面积为3−1=2.
故选D.
本题考查了反比例函数y=中k的几何意义，即过双曲线上任意一点引x轴、y轴垂线，所得矩形面积为|k|，解本题的关键是正确理解k的几何意义.
6、B
【解析】
根据加权平均数的计算方法：先求出所有糖果的总钱数，再除以糖果的总质量，即可得出答案.
【详解】
解：售价应定为: （元）；故选：B
本题考查的是加权平均数的求法，本题易出现的错误是对加权平均数的理解不正确，而求6，7，8这三个数的平均数.
7、C
【解析】
分3>x+2即x<1和31两种情况，根据新定义列出不等式求解可得．
【详解】
当3>x+2,即x<1时,3(x+2)+x+2>0，
解得：x>−2，
∴−2当31时,3(x+2)−(x+2)>0，
解得：x>−2，
∴x>1，
综上，−21，
故选：C.
8、D
【解析】
连接AC、CE，CE交BD于P，此时AP+PE的值最小，求出CE长，即可求出答案．
【详解】
解：连接AC、CE，CE交BD于P，连接AP、PE，
∵四边形ABCD是正方形，
∴OA＝OC，AC⊥BD，即A和C关于BD对称，
∴AP＝CP，
即AP+PE＝CE，此时AP+PE的值最小，
所以此时△PAE周长的值最小，
∵正方形ABCD的边长为4，点E在边AB上，AE＝1，
∴∠ABC＝90°，BE＝4﹣1＝3，
由勾股定理得：CE＝5，
∴△PAE的周长的最小值是AP+PE+AE＝CE+AE＝5+1＝6，
故选D．
本题考查了正方形的性质与轴对称——最短路径问题，知识点比较综合，属于较难题型.
二、填空题（本大题共5个小题，每小题4分，共20分）
9、
【解析】
直接根据一次函数图象与几何变换的有关结论求解．
【详解】
直线y=2x向上平移2个单位后得到的直线解析式为y=2x+2.
故答案为y=2x+2.
此题考查一次函数图象与几何变换，解题关键在于掌握平移的性质
10、
【解析】
延长EF交CB于M，连接DM，根据正方形的性质得到AD=DC，∠A=∠BCD=90°，由折叠的性质得到∠DFE=∠DFM=90°，通过Rt△DFM≌Rt△DCM，于是得到MF=MC．由等腰三角形的性质得到∠MFC=∠MCF由余角的性质得到∠MFC=∠MBF，于是求得MF=MB，根据勾股定理即可得到结论．
【详解】
如图，
延长EF交CB于M，连接DM，
∵四边形ABCD是正方形，
∴AD=DC，∠A=∠BCD=90°，
∵将△ADE沿直线DE对折得到△DEF，
∴∠DFE=∠DFM=90°，
在Rt△DFM与Rt△DCM中，，
∴Rt△DFM≌Rt△DCM（HL），
∴MF=MC，
∴∠MFC=∠MCF，
∵∠MFC+∠BFM=90°，∠MCF+∠FBM=90°，
∴∠MFB=∠MBF，
∴MB=MC，
∴MF=MC=BM=，设AE=EF=x，
∵BE2+BM2=EM2，
即（1-x）2+（）2=（x+）2，
解得：x=，
∴AE=，
故答案为：．
本题考查了翻折变换-折叠问题，正方形的性质，全等三角形的判定和性质，勾股定理，正确的作出辅助线是解题的关键．
11、1
【解析】
∵骑车的学生所占的百分比是×100%=35%，
∴步行的学生所占的百分比是1﹣10%﹣15%﹣35%=40%，
∴若该校共有学生1500人，则据此估计步行的有1500×40%=1（人），
故答案为1．
12、正方
【解析】
此类题根据矩形性质，三角形内角和定理及角平分线定义得到所求的四边形的各个角为90°，进而求解．
【详解】
∵AF，BE是矩形的内角平分线．
∴∠ABF=∠BAF-90°．
故∠1=∠2=90°．
同理可证四边形GMON四个内角都是90°，则四边形GMON为矩形．
又∵有矩形ABCD且AF、BE、DK、CJ为矩形ABCD四角的平分线，
∴有等腰直角△DOC，等腰直角△AMD，等腰直角△BNC，AD=BC．
∴OD=OC，△AMD≌△BNC，
∴NC=DM，
∴NC-OC=DM-OD，
即OM=ON，
∴矩形GMON为正方形，
故答案为正方．
本题考查的是矩形性质，角平分线定义，联系三角形内角和的知识可求解．
13、1
【解析】
任何不为零的数的零次方都为1.
【详解】
任何不为零的数的零次方都等于1.
=1
本题考查零指数幂，熟练掌握计算法则是解题关键.
三、解答题（本大题共5个小题，共48分）
14、（1）证明见解析；（2）证明见解析；（3）BD//AE，BD=AE.
【解析】
（1）根据平行线的性质得到∠ABC=∠EKC，∠AMB=∠ECK，得到△ABM∽△EKC；
（2）根据相似三角形的性质得到比例式，计算即可；
（3）根据相似三角形的性质得到DE=AB，得到四边形ABDE是平行四边形，根据平行是四边形的性质解答．
【详解】
(1)证明：∵，
∴，
∵，
∴，
∴；
(2)证明：∵，
∴，
∴，
∵是的中线，
∴，
∴；
(3)解：，，
∵，
∴，
∵，
∴，
∵，
∴四边形是平行四边形，
∴，.
本题考查的是相似三角形的判定和性质、平行四边形的判定和性质，掌握相似三角形的判定定理和性质定理是解题的关键．
15、 (1)m=0.2，n=20；（2）图见解析；（3）50%.
【解析】
（1）根据成绩在105≤x＜120的频数和频率可以求得本次调查的人数，从而可以求得m、n的值；
（2）根据（1）中n的值，可以将频数分布直方图补充完整；
（3）根据频数分布表中的数据可以得到本次测试的优秀率．
【详解】
解：（1）由表可知：105≤x＜120的频数和频率分别为15、0.3，
∴本次调查的人数为：15÷0.3=50，
∴m=10÷50=0.2，
n=50×0.4=20，
故答案为：0.2，20；
（2）由（1）知，n=20，
补全完整的频数分布直方图如右图所示；
（3）成绩不低于120分为优秀，则本次测试的优秀率:（0.4+0.1）×100%=50%，
答：本次测试的优秀率是50%．
本题考查频数分布直方图、频数分布表，解答本题的关键是明确题意，利用数形结合的思想解答．
16、（1）科普书每本15元，文学书每本10元；（2）至少购买文学书8本.
【解析】
（1）设文学书的价格为每本元，则文学书每本元，再根据科普书比所买的文学书少2本的等量关系，列分式方程，解分式方程即可；
（2）设购买文学书本，则购买科普书（20-y）本，根据购买总费用不超过260元，列出不等式，再解不等式，即可确定答案.
【详解】
（1）设文学书的价格为每本元，
解之得：
经检验x=10是原方程的根.
科普书的价格＝10×=15元；
答：科普书每本15元，文学书每本10元.
（2）设购买文学书本，则
解之得：y≥8
答：至少购买文学书8本.
本题考查了运用分式方程和不等式解决实际问题，解得这类题的关键是设出合适的未知数，表示相关量，然后根据等量或不等关系列出方程解答.
17、不等式组的解集是，数轴表示见解析.
【解析】
分别求出各不等式的解集，再求出其公共解集，并在数轴上表示出来即可．
【详解】
，
解不等式，得，
解不等式，得，
不等式组的解集是．
解集在数轴上表示如图：
.
本题考查的是解一元一次不等式组，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．
18、（1）40人，117;（2）B;（3）30人.
【解析】
（1）根据B等级的学生数和所占的百分比可以求得本次调查的学生数；求出C的人数，再计算出所占比例即可求出对应的扇形的圆心角的度数；从而可以将条形统计图补充完整；
（2）根据统计图中的数据可以得到所抽取学生的足球运球测试成绩的中位数落在哪个等级；
（3）根据统计图中的数据可以求得足球运球测试成绩达到A级的学生有多少人．
【详解】
（1）18÷45%=40，
即在这次调查中一共抽取了40名学生，
C等级的人数为：40-4-18-5=13，
在扇形统计图中，C对应的扇形的圆心角是：360°×=117°，
补全的条形统计图如图所示：
（2）由统计图可知，
所抽取学生的足球运球测试成绩的中位数落在B等级，
故答案为B；
（5）300×=30（人），
答：足球运球测试成绩达到A级的学生有30人．
本题考查条形统计图、扇形统计图、用样本估计总体、中位数，解答本题的关键是明确题意，利用数形结合的思想解答．
一、填空题（本大题共5个小题，每小题4分，共20分）
19、
【解析】
根据矩形的性质可得∠AEB=∠EBC，由BE是∠ABC的角平分线可得∠ABE=∠EBC，即可证明∠ABE=∠AEB，进而可得AE=AB，即可求出DE的长，利用勾股定理即可求出CE的长.
【详解】
∵ABCD是矩形，
∴AD//BC，CD=AB=2，AD=BC=3，
∴∠AEB=∠EBC，
∵BE是∠ABC的角平分线，
∴∠ABE=∠EBC，
∴∠ABE=∠AEB，
∴AE=AB=2，
∴DE=AD-AE=1，
在Rt△CDE中，CE==，
故答案为：
本题考查矩形的性质、勾股定理及等腰三角形的判定和性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．
20、5
【解析】
∵多边形的每个外角都等于72°，
∵多边形的外角和为360°，
∴360°÷72°=5，
∴这个多边形的边数为5.
故答案为5.
21、50
【解析】
因为平行四边形的对角相等,所以∠C=50°,故答案为: 50°.
22、6
【解析】
由题意可知，MN是三角形ABC的中位线，然后依据三角形的中位线定理求解即可。
【详解】
解：∵M、N分别为AB、BC的中点，
∴MN是△ABC的中位线，
∴.AC=2MN=2×3=6.
故答案为：6.
本题主要考查的是三角形的中位线定理，熟练掌握三角形的中位线定理是解题的关键.
23、或
【解析】
利用反比例函数增减性分析得出答案．
【详解】
解：且，
时，，
在第三象限内，随的增大而减小，
；
当时，，在第一象限内，随的增大而减小，
则，
故的取值范围是：或．
故答案为：或．
此题主要考查了反比例函数图象上点的坐标特征，正确掌握反比例函数增减性是解题关键．
二、解答题（本大题共3个小题，共30分）
24、答案见解析．
【解析】
试题分析：欲证明AC∥BD，只要证明∠A=∠B，只要证明△DEB≌△CFA即可．
试题解析：∵DE⊥AB，CF⊥AB，∴∠DEB=∠AFC=90°，∵AE=BF，∴AF=BE，在△DEB和△CFA中，∵DE=CF，∠DEB=∠AFC，AF=BE，△DEB≌△CFA，∴∠A=∠B，∴AC∥DB．
考点：全等三角形的判定与性质．
25、（1）；（2）或；(3),理由见解析。
【解析】
（1）联立两函数即可求出C点坐标;
（2）根据题意写出M,D,E的坐标，再根据即可列式求解；
（3）过作，交的延长线于，设交于点，得到得为等腰直角三角形，再证明，故可得，即可求解.
【详解】
（1）联立，解得
∴
（2）
依题意得
解得或
(3),理由如下：
过作，交的延长线于，设交于点
易得为等腰直角三角形，
易得
此题主要考查一次函数的应用，解题的关键是根据题意作出辅助线、熟知一次函数的图像及全等三角形的判定与性质.
26、（1）证明见解析；（2）t=1，（3）不存在某个时刻t，使四边形EHFG为矩形．
【解析】
（1）根据菱形的性质得到∠B=∠D，AD=BC，AB∥DC，推出△ADF≌△CBE，根据全等三角形的性质得到∠DFA=∠BEC，根据平行线的判定定理即可得到结论；
（2）过D作DM⊥AB于M，连接GH，EF，推出四边形AECF是平行四边形，根据菱形的判定定理即可得到四边形EGFH是菱形，证得四边形DMEF是矩形，于是得到ME=DF=t列方程即可得到结论；
（3）不存在，假设存在某个时刻t，使四边形EHFG为矩形，根据矩形的性质列方程即可得到结果．
【详解】
（1）证明：∵动点E、F同时运动且速度相等，
∴DF=BE，
∵四边形ABCD是菱形，
∴∠B=∠D，AD=BC，AB∥DC，
在△ADF与△CBE中，

∴△ADF≌△CBE，
∴∠DFA=∠BEC，
∵AB∥DC，
∴∠DFA=∠FAB，
∴∠FAB=∠BEC，
∴AF∥CE；
（2）过D作DM⊥AB于M，连接GH，EF，
∴DF=BE=t，
∵AF∥CE，AB∥CD，
∴四边形AECF是平行四边形，
∵G、H是AF、CE的中点，
∴GH∥AB，
∵四边形EGFH是菱形，
∴GH⊥EF，
∴EF⊥AB，∠FEM=90°，
∵DM⊥AB，
∴DM∥EF，
∴四边形DMEF是矩形，
∴ME=DF=t，
∵AD=4，∠DAB=60°，DM⊥AB，
∴
∴BE=4﹣2﹣t=t，
∴t=1，
（3）不存在，假设存在某个时刻t，使四边形EHFG为矩形，
∵四边形EHFG为矩形，
∴EF=GH，
∴EF2=GH2，
即解得t=0，0＜t＜4，
∴与原题设矛盾，
∴不存在某个时刻t，使四边形EHFG为矩形．
属于四边形的综合题，考查全等三角形的判定与性质，菱形的性质，矩形的判定等，掌握菱形的性质，矩形的判定是解题的关键.
题号
一
二
三
四
五
总分
得分