安徽省淮北市西园中学2024年数学九上开学经典模拟试题【含答案】

这是一份安徽省淮北市西园中学2024年数学九上开学经典模拟试题【含答案】，共29页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）如图是某件商晶四天内的进价与售价的折线统计图．那么售出每件这种商品利润最大的是（ ）
A．第一天B．第二天C．第三天D．第四天
2、（4分）下列叙述，错误的是（ ）
A．对角线互相垂直且相等的平行四边形是正方形
B．对角线互相垂直平分的四边形是菱形
C．对角线互相平分的四边形是平行四边形
D．对角线相等的四边形是矩形
3、（4分）下列各组线段中，能够组成直角三角形的一组是（ ）
A．1，2，3B．2，3，4C．4，5，6D．1，，
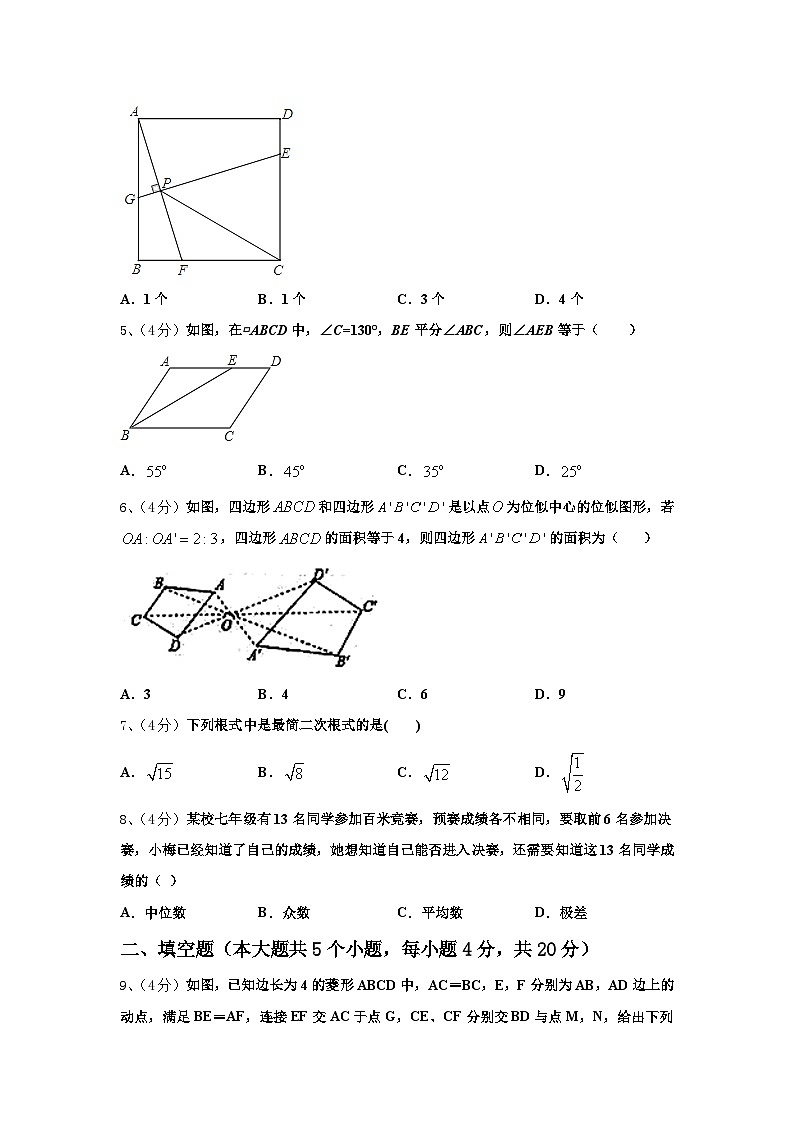
4、（4分）如图，已知四边形ABCD是边长为4的正方形，E为CD上一点，且DE＝1，F为射线BC上一动点，过点E作EG⊥AF于点P，交直线AB于点G．则下列结论中：①AF＝EG；②若∠BAF＝∠PCF，则PC＝PE；③当∠CPF＝45°时，BF＝1；④PC的最小值为﹣1．其中正确的有（ ）
A．1个B．1个C．3个D．4个
5、（4分）如图，在▱ABCD中，∠C=130°，BE平分∠ABC，则∠AEB等于（ ）
A．B．C．D．
6、（4分）如图，四边形和四边形是以点为位似中心的位似图形，若，四边形的面积等于4，则四边形的面积为（ ）
A．3B．4C．6D．9
7、（4分）下列根式中是最简二次根式的是( )
A．B．C．D．
8、（4分）某校七年级有13名同学参加百米竞赛，预赛成绩各不相同，要取前6名参加决赛，小梅已经知道了自己的成绩，她想知道自己能否进入决赛，还需要知道这13名同学成绩的（ ）
A．中位数B．众数C．平均数D．极差
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）如图，已知边长为4的菱形ABCD中，AC＝BC，E，F分别为AB，AD边上的动点，满足BE＝AF，连接EF交AC于点G，CE、CF分别交BD与点M，N，给出下列结论：①∠AFC＝∠AGE；②EF＝BE+DF；③△ECF面积的最小值为3，④若AF＝2，则BM＝MN＝DN；⑤若AF＝1，则EF＝3FG；其中所有正确结论的序号是_____．
10、（4分）如果一组数据：5，，9，4的平均数为6，那么的值是_________
11、（4分）二次三项式是一个完全平方式，则k=_______.
12、（4分）已知点P（-1，m）,Q（-2，n）都在反比例函数的图像上，则m____n（填“>”或“60°，故△ADP不可能是等边三角形．
【详解】
（1）补全的图形，如图所示．
（2）AG=DH．
证明：∵四边形ABCD是菱形，
∴，∥，．
∵点为点关于的对称点，
∴垂直平分．
∴，．
∴．
又∵，
∴．
∵，，
∴．
∴△≌△．
∴．
（3）不存在．
理由如下：
由（2）可知，∠DAG=∠CDH，∠G=∠GAB，
∴∠DPA=∠PDG＋∠G=∠DAG+∠GAB=70°>60°．
∴△ADP不可能是等边三角形．
【点睛】本题考核知识点：菱形，轴对称,等边三角形. 解题关键点：此题比较综合，要熟记菱形性质，全等三角形的判定和性质，轴对称性质，等边三角形判定.
一、填空题（本大题共5个小题，每小题4分，共20分）
19、1
【解析】
分析：根据矩形的性质、结合点A的坐标得到点D的横坐标为2，点B的纵坐标为1，根据反比例函数解析式求出点D的坐标，点B的坐标，根据矩形的周长公式计算即可．
详解：∵四边形ABCD是矩形，点A的坐标为（2，1），
∴点D的横坐标为2，点B的纵坐标为1，
当x=2时，y==3，
当y=1时，x=6，
则AD=3-1=2，AB=6-2=4，
则矩形ABCD的周长=2×（2+4）=1，
故答案为1．
点睛：本题考查的是反比例函数图象上点的坐标特征、矩形的性质，掌握反比例函数图象上点的坐标特征是解题的关键．
20、（3，）．
【解析】
试题分析：先利用两点间的距离公式计算出AD=2，再根据菱形的性质得到CD=AD=2，CD∥AB，然后根据平行于x轴的直线上的坐标特征写出C点坐标．
解：∵点D的坐标为（1，），
∴AD==2，
∵四边形ABCD为菱形，
∴CD=AD=2，CD∥AB，
∴C点坐标为（3，）．
故答案为（3，）．
21、17或-7
【解析】
利用完全平方公式的结构特征判断即可确定出k的值．
【详解】
解：∵二次三项式4x2-（k-5）x+9是完全平方式，
∴k-5=±12，
解得：k=17或k=-7，
故答案为：17或-7
此题考查了完全平方式，熟练掌握完全平方公式是解本题的关键．
22、
【解析】
过作，利用正方形的性质和全等三角形的判定得出，进而利用勾股定理解答即可．
【详解】
解：过作，
正方形，
，，
，
，
，且，，
，
，，
当时，的最小值为
故答案为：
本题考查正方形的性质，关键是利用正方形的性质和全等三角形的判定得出．
23、3或-1
【解析】
据题意得，∵（x+2）*5=（x+2）2-52∴x2+4x-21=0，∴（x-3）（x+1）=0，∴x=3或x=-1．
二、解答题（本大题共3个小题，共30分）
24、（1）y1=4500x+1500；y2=4800x；（2）答案见解析；（3）从甲商场买4台，从乙商场买6台时，总运费最少，最少运费是560元
【解析】
（1）根据题意列出函数解析式即可；
（2）①若甲商场购买更优惠，可得不等式4500x+1500＜4800x，解此不等式，即可求得答案；
②若乙商场购买更优惠，可得不等式4500x+1500＞4800x，解此不等式，即可求得答案；
③若两家商场收费相同，可得方程4500x+1500=4800x，解此方程，即可求得答案；
（3）根据题意列出函数解析式，再根据增减性即可进行解答．
【详解】
解：（1）y1=6000+（1-25%）×6000（x-1）=4500x+1500；
y2=（1-20%）×6000x=4800x；
（2）设学校购买x台电脑，
若到甲商场购买更优惠，则：
4500x+1500＜4800x，
解得：x＞5，
即当购买电脑台数大于5时，甲商场购买更优惠；
若到乙商场购买更优惠，则：
4500x+1500＞4800x，
解得：x＜5，
即当购买电脑台数小于5时，乙商场购买更优惠；
若两家商场收费相同，则：
4500x+1500=4800x，
解得：x=5，
即当购买5台时，两家商场的收费相同；
（3）w=50a+（10-a）60=600-10a，
当a取最大时，费用最小，
∵甲商场只有4台，
∴a取4，W=600-40=560，
即从甲商场买4台，从乙商场买6台时，总运费最少，最少运费是560元．
本题考查了一元一次不等式实际应用问题，涉及了不等式与方程的解法，解题的关键是理解题意，根据题意求得函数解析式，然后利用函数的性质求解．
25、（1）见解析，；（2）四边形是菱形，理由见解析
【解析】
（1）由菱形的性质可得AD=CD，∠A=∠C=45°，∠ADC=135°，由折叠的性质可得AE=DE=AD，GE⊥AD，∠A=∠GDA=45°，DF=FC=CD，HF⊥CD，∠C=∠CDH=45°，由四边形的内角和定理可求解；
（2）由题意可证GE∥DH，GD∥HF，可证四边形DGOH是平行四边形，由“ASA”可证△DEG≌△DFH，可得DG=DH，即可证四边形DGOH是菱形．
【详解】
解：（1）如图，延长EG，FH交于点O，
∵四边形ABCD是菱形，∠A=45°，
∴AD=CD，∠A=∠C=45°，∠ADC=135°，
∵把△AEG翻折，使得点A与点D重合，折痕为EG；把△CFH翻折，使得点C与点D重合，折痕为FH，
∴AE=DE=AD，GE⊥AD，∠A=∠GDA=45°，DF=FC=CD，HF⊥CD，∠C=∠CDH=45°，
∵∠EOF+∠OED+∠OFD+∠ADC=360°，
∴∠EOF=360°-90°-90°-135°=45°；
（2）四边形是菱形．理由如下：
∵∠ADC=135°，∠ADG=∠CDH=45°，
∴∠GDC=∠ADH=90°，且GE⊥AD，HF⊥CD，
∴GE∥DH，GD∥HF，
∴四边形DGOH是平行四边形，
∵AE=DE=AD，DF=FC=CD，AD=CD，
∴DE=DF，且∠ADG=∠CDH=45°，∠DEG=∠DFH=90°，
∴△DEG≌△DFH（ASA）
∴DG=DH，
∴四边形DGOH是菱形．
本题考查了翻折变换，菱形的判定和性质，平行四边形的判定和性质，以及全等三角形的判定和性质，灵活运用折叠的性质进行解题是本题的关键．
26、（1）A（1，0），B（1，1）；（2）OD⊥BF，理由见解析；（3）当P点为线段DE的三等分点时，AF的长度为2或2．
【解析】
（1）利用正方形的性质得出OA=AB=1，即可得出结论；
（2）利用SAS判断出△AOD≌△BAF，进而得出∠AOD=∠BAF，即可得出结论；
（3）先表示出BD，DP，再判断出△BDP∽△BAF，得出，代入解方程即可得出结论。
【详解】
（1）∵四边形OABC是正方形，
∴BC⊥OC，AB⊥OA，OB＝AB＝BC＝OC，
∵OC＝1，
∴BC＝AB＝1，
∴A（1，0），B（1，1）；
（2）OD⊥BF，理由：如图，延长OD交BF于G，
∵四边形ADEF是正方形，
∴AD＝AF，∠BAF＝∠OAD，
在△AOD和△BAF中， ，
∴△AOD≌△BAF（SAS），
∴∠AOD＝∠BAF，
∴∠BAF+∠AFB＝90°，
∴∠AOD+AFB＝90°，
∴∠OGF＝90°，
∴OD⊥BF；
（3）设正方形ADEF的边长为x，
∴AF＝AD＝DE＝x，
∴BD＝AB﹣AD＝1﹣x，
∵点P是DE的三等分点，
∴DP＝AF＝x或DP＝AF＝x
∵DE∥AF，
∴△BDP∽△BAF，
∴，
∴或 ，
∴x＝2或x＝2，
当P点为线段DE的三等分点时，AF的长度为2或2．
本题是四边形综合题，主要考查了正方形的性质，全等三角形的判定和性质，垂直的判定，相似三角形的判定和性质，用方程的思想解决问题是解本题的
题号
一
二
三
四
五
总分
得分
批阅人
商场
优惠条件
甲商场
第一台按原价收费，其余的每台优惠25%
乙商场
每台优惠20%