苏科版数学七年级上册全程通关培优(专项卷+章节复习+期中期末备考)专题3.3代数式(章节复习+能力强化卷)特训（学生版+解析）

这是一份苏科版数学七年级上册全程通关培优(专项卷+章节复习+期中期末备考)专题3.3代数式(章节复习+能力强化卷)特训（学生版+解析），共31页。试卷主要包含了3 代数式，7aC．1，25a等内容，欢迎下载使用。

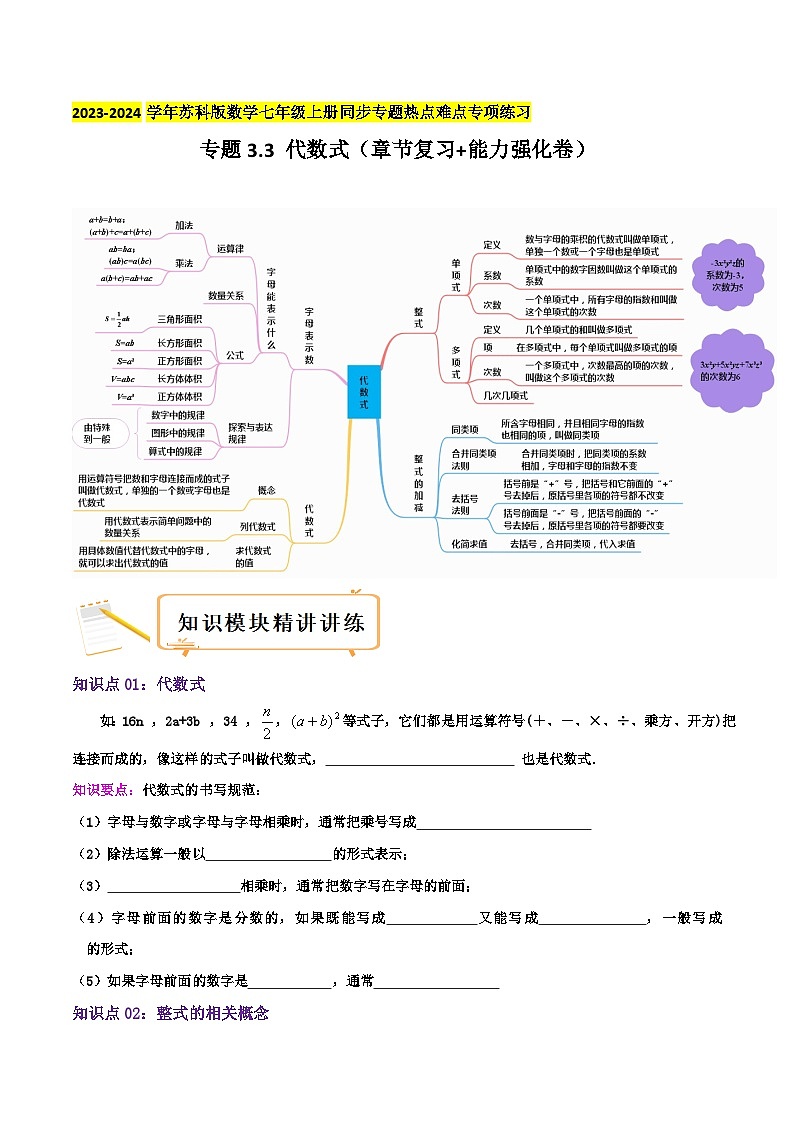
知识点01：代数式
如：16n ，2a+3b ，34 ，，等式子，它们都是用运算符号(＋、－、×、÷、乘方、开方)把 连接而成的，像这样的式子叫做代数式， 也是代数式．
知识要点：代数式的书写规范：
（1）字母与数字或字母与字母相乘时，通常把乘号写成
（2）除法运算一般以 的形式表示；
（3） 相乘时，通常把数字写在字母的前面；
（4）字母前面的数字是分数的，如果既能写成 又能写成 ，一般写成 的形式；
（5）如果字母前面的数字是 ，通常
知识点02：整式的相关概念
1．单项式：由 组成的代数式叫做单项式， 也是单项式．
知识要点：（1）单项式的系数是指
（2）单项式的次数是指单项式中 ．
2．多项式： 叫做多项式．在多项式中，每个单项式叫做 ．
知识要点：（1）在多项式中， 叫做常数项．
（2）多项式中 的次数，就是这个多项式的次数．
（3）多项式的次数是 次，有 个单项式，我们就把这个多项式称为 ．
3. 多项式的降幂与升幂排列：
把一个多项式按某一个字母的指数从大到小的顺序排列起来，叫做把这个多项式按这个字
母 ．另外，把一个多项式按某一个字母的指数从小到大的顺序排列起来，叫做把这个多项式按这个字母
知识要点：（1）利用 重新排列时，各项应连同它的符号一起移动位置；
（2）含有多个字母时，只按给定的字母进行 排列．
4．整式：单项式和多项式统称为整式．
知识点03：整式的加减
1．同类项：所含 相同，并且 也相同的项叫做同类项．所有的 都是同类项．
知识要点：辨别同类项要把准“两相同，两无关”：
（1）“两相同”是指：①所含 相同；② 相同；
（2）“两无关”是指：①与 无关；②与 无关．
2．合并同类项：把 ，叫做合并同类项．
知识要点：合并同类项时，只是 相加减，所得结果作为系数， 保持不变．
3．去括号法则：括号前面是“+”，把括号和它前面的“+”去掉后，原括号里各项的符号都 ；括号前面是“-”，把括号和它前面的“-”号去掉后，原括号里各项的符号都要 ．
4．添括号法则：添括号后，括号前面是“+”，括号内各项的符号都 ；添括号后，括号前面是“-”，括号内各项的符号都要 ．
5．整式的加减运算法则：几个整式相加减，通常用括号把每一个整式括起来，再用 连接，然后
一、选择题(共10题；每题2分，共20分)
1．（2分）（2023七上·龙华期末）某种商品进价为a元，在销售旺季，提价30%销售，旺季过后，商品以7折价格开展促销活动，这时一件商品的售价为（ ）
A．aB．0.7aC．1.03aD．0.91a
2．（2分）（2023七上·苍南期末）图1是由3个相同小长方形拼成的图形其周长为24，图2中的长方形内放置10个相同的小长方形，则长方形的周长为（ ）
A．B．C．D．
3．（2分）（2023七上·洛川期末）已知，，则代数式的值为
A．38B．35C．-35D．-32
4．（2分）（2022七上·赵县期末）嘉琪在进行解方程的思维训练，其中有一个方程“2y-=y+■”中的■没印清晰，嘉琪问老师，老师只是说：“■是一个有理数，该方程的解与当×= 2时代数式5(x-1)-2(x- 2)-4的值相同．”嘉琪很快补上了这个有理数．你认为嘉琪补的这个有理数是（ ）
A．1B．-1C．2D．-2
5．（2分）（2023七上·洛川期末）已知x+2y＝7，4m﹣3n＝8，则代数式（9n﹣4y）﹣2（6m+x）+3的值为（ ）
A．38B．35C．﹣35D．﹣32
6．（2分）（2023七上·澄城期末）下面四个整式中，不能表示图中阴影部分面积的是（ ）
A．B．
C．D．
7．（2分）（2022七上·南宁月考）按如图所示的运算程序，若开始输入x的值为343，则第2022次输出的结果为（ ）
A．343B．1C．7D．49
8．（2分）（2021七上·奉化期末）已知长方形ABCD， ， ，将两张边长分别为a和b（ ）的正方形纸片按图1，图2两种方式放置（图1，图2中两张正方形纸片均有部分重叠），矩形中未被这两张正方形纸片覆盖的部分用阴影表示，设图1中阴影部分的面积为 ，图2中阴影部分的面积为 ．当 时，AB的值是（ ）
A．7B．8C．9D．10
9．（2分）（2021七上·普宁期中）如图所示，在这个数据运算程序中，如果开始输入的x的值为10，那么第1次输出的结果是5，返回进行第二次运算，那么第2次输出的结果是16，……以此类推，第204次输出的结果是（ ）
A．1B．2C．4D．5
10．（2分）（2022·宁波模拟）将四张边长各不相同的正方形纸片按如图方式放入矩形 内（相邻纸片之间互不重叠也无缝隙），未被四张正方形纸片覆盖的部分用阴影表示.设右上角与左下角阴影部分的周长的差为 .若知道 的值，则不需测量就能知道周长的正方形的标号为（ ）
A．①B．②C．③D．④
二、填空题(共10题；每题2分，共20分)
11．（2分）（2023七上·杭州期末）单项式的系数是 ；次数是 .
12．（2分）（2023七上·江北期末）若，则的值是 .
13．（2分）（2023七上·兰溪期末）如图所示，一块砖的外墙面积为x，那么图中残缺墙面的面积为 .
14．（2分）（2023七上·慈溪期末）已知，，则 .
15．（2分）（2023七上·义乌期末）有一个长方体水箱，从里面量得它的深度为，底面长为，宽为，水箱里已盛有深度为的水.若往水箱里放入一个棱长为的立方体铁块，则水箱的水深为 .
16．（2分）（2021七上·安吉期末）《孙子算经》是中国古代时期重要的数学专著，其中包含了“鸡兔同笼”“物不知数”等许多有趣的数学问题．《孙子算经》中记载：“今有物不知数，三三数之剩二，五五数之剩三，七七数之剩二，问物几何?”其译文为：“有一个正整数，除以3余2，除以5余3，除以7余2，求符合条件的正整数．”请用含k (k为自然数）的代数式表示满足条件的所有正整数 .
17．（2分）（2021七上·深圳期中）数学真奇妙：两个有理数a和b，如果分别计算a＋b，a﹣b，ab，的值，发现有三个结果恰好相同，则b＝ ．
18．（2分）（2020七上·江夏月考）已知a、b、c是非零有理数，且a＋b＋c＝0，abc＜0，求 ＝ .
19．（2分）（2020七上·海曙月考）下图是一个程序运算图，若开始输入的数是125，则2020次之后输出的数是 .
20．（2分）（2020七上·南浔期末）已知长方形ABCD，AD>AB，AD=10，将两张边长分别为a和b（a>b） 的正方形纸片按图1，图2两种方式放置（图1，图2中两张正方形纸片均有部分重叠），矩形中未被这两张正方形纸片覆盖的部分用阴影表示，设图1中阴影部分的面积为S1，图2中阴影部分的面积为S2，当S2-S1=3b时，AB= 。
三、解答题(共8题；共61分)
21．（5分）（2022七上·利川期末）化简下列各式：
（1）（2分）； （2）（3分）.
22．（5分）（2022七上·昌邑期末）一块三角尺的形状和尺寸如图所示，如果圆孔的半径是r，三角尺的厚度是h，用式子表示这块三角尺的体积V．若，求V的值（取3）．
（5分）（2022七上·丰满期末）历史上的数学巨人欧拉最先把关于x的多项式用记号来表示，把x等于某数m时的多项式的值用来表示．例如，对于多项式，当时，多项式的值为，若，求的值．
24．（8分）（2020七上·高平期中）某电器商销售一种微波炉和电磁炉，微波炉每台定价800元，电磁炉每台定价200元．“双十一”期间商场决定开展促销活动，活动期间向客户提供两种优惠方案．
方案一：买一台微波炉送一台电磁炉；方案二：微波炉和电磁炉都按定价的90%付款．
现某客户要到该卖场购买微波炉2台，电磁炉x台（x＞2）．
（1）（4分）若该客户按方案一购买，需付款 元．（用含x的代数式表示）；若该客户按方案二购买，需付款 元．（用含x的代数式表示）
（2）（2分）若x＝5时，通过计算说明此时按哪种方案购买较为合算？
（3）（2分）当x＝5时，你能给出一种更为省钱的购买方案吗？试写出你的购买方法．
25．（8分）（2023七上·龙华期末）甲、乙两家超市以相同的价格出售同样的商品，但为了吸引顾客，各自推出不同的优惠方案.在甲超市累计购买商品超过400元后，超出的部分按原价收取：在乙超市购买商品只按原价的收取.设某顾客预计累计购物x元.
（1）（4分）当时，分别用代数式表示顾客在两家超市购物所付的费用；
（2）（4分）当时，该顾客应选择哪一家超市购物比较合算?说明理由.
26．（8分）（2023七上·武义期末）如图，两叠规格相同的杯子整齐地叠放在桌面上，请根据图中给出的数据信息，解答下列问题：
（1）（4分）按如图所示叠放一起时，相邻两个杯子杯口之间的高度相差 cm.
（2）（4分）若x个杯子按如图所示整齐叠放在桌面上，求这些杯子的顶部距离桌面的距离（用含x的代数式表示）.当时，求这些杯子的顶部距离桌面的距离.
27．（12分）（2023七上·成都期末）已知是最小的正整数，，满足，且，，分别对应数轴上的点，，．
（1）（4分）请直接写出，，的值： ， ， ．
（2）（3分）若点为一动点，从点出发以每秒2个单位长度的速度向右运动，则点运动几秒后，点到点的距离是点到点的距离的2倍？
（3）（5分）点以每秒1个单位长度的速度向左运动，同时点和点分别以每秒2个单位长度和5个单位长度的速度向右运动．点与点之间的距离表示为，点与点之间的距离表示为假设运动时间为，的值是否随着时间的变化而改变？若变化，请说明理由；若不变，请求其值．
28．（10分）（2022七上·大田期中）如图
（1）（3分）【操作感知】如图①，长方形透明纸上有一条数轴，是周长为4的圆的直径，点与数轴原点重合，将圆从原点出发沿数轴正方向滚动1周，点落在数轴上的点处；将圆从原点出发沿数轴负方向滚动半周，点落在数轴上的点处，折叠长方形透明纸，使数轴上的点与点重合，此时折痕与数轴交点表示的数为 .
（2）（2分）【建立模型】折叠长方形透明纸，使得数轴上表示数的点与表示数的点重合，则折痕与数轴交点表示的数为 （用含，的代数式表示）.
（3）（2分）【问题解决】若，，为数轴上不同的三点，点表示的数为，点表示的数为-2，如果，，三点中的一点到其余两点的距离相等，求点表示的数；
（4）（3分）如图②，若是周长为的圆的直径，点与数轴原点重合，将圆从原点出发沿数轴正方向滚动2周，点落在数轴上的点处；将圆从原点出发沿数轴负方向滚动周，点落在数轴上的点处.将此长方形透明纸沿，剪开，将点，之间一段透明纸对折，使其左、右两端重合，这样连续对折次后，再将其展开，求最右端折痕与数轴交点表示的数.
2023-2024学年苏科版数学七年级上册同步专题热点难点专项练习
专题3.3 代数式（章节复习+能力强化卷）
知识点01：代数式
如：16n ，2a+3b ，34 ，，等式子，它们都是用运算符号(＋、－、×、÷、乘方、开方)把数和表示数的字母连接而成的，像这样的式子叫做代数式，单独的一个数或一个字母也是代数式．
知识要点：代数式的书写规范：
（1）字母与数字或字母与字母相乘时，通常把乘号写成“· ”或省略不写；
（2）除法运算一般以分数的形式表示；
（3）字母与数字相乘时，通常把数字写在字母的前面；
（4）字母前面的数字是分数的，如果既能写成带分数又能写成假分数，一般写成假分数的形式；
（5）如果字母前面的数字是1，通常省略不写．
知识点02：整式的相关概念
1．单项式：由数与字母的乘积组成的代数式叫做单项式，单独的一个数或一个字母也是单项式．
知识要点：（1）单项式的系数是指单项式中的数字因数．
（2）单项式的次数是指单项式中所有字母的指数和．
2．多项式：几个单项式的和叫做多项式．在多项式中，每个单项式叫做多项式的项．
知识要点：（1）在多项式中，不含字母的项叫做常数项．
（2）多项式中次数最高的项的次数，就是这个多项式的次数．
（3）多项式的次数是n次，有m个单项式，我们就把这个多项式称为n次m项式．
3. 多项式的降幂与升幂排列：
把一个多项式按某一个字母的指数从大到小的顺序排列起来，叫做把这个多项式按这个字母降幂排列．另外，把一个多项式按某一个字母的指数从小到大的顺序排列起来，叫做把这个多项式按这个字母升幂排列．
知识要点：（1）利用加法交换律重新排列时，各项应连同它的符号一起移动位置；
（2）含有多个字母时，只按给定的字母进行降幂或升幂排列．
4．整式：单项式和多项式统称为整式．
知识点03：整式的加减
1．同类项：所含字母相同，并且相同字母的指数也相同的项叫做同类项．所有的常数项都是同类项．
知识要点：辨别同类项要把准“两相同，两无关”：
（1）“两相同”是指：①所含字母相同；②相同字母的指数相同；
（2）“两无关”是指：①与系数无关；②与字母的排列顺序无关．
2．合并同类项：把多项式中的同类项合并成一项，叫做合并同类项．
知识要点：合并同类项时，只是系数相加减，所得结果作为系数，字母及字母的指数保持不变．
3．去括号法则：括号前面是“+”，把括号和它前面的“+”去掉后，原括号里各项的符号都不改变；括号前面是“-”，把括号和它前面的“-”号去掉后，原括号里各项的符号都要改变．
4．添括号法则：添括号后，括号前面是“+”，括号内各项的符号都不改变；添括号后，括号前面是“-”，括号内各项的符号都要改变．
5．整式的加减运算法则：几个整式相加减，通常用括号把每一个整式括起来，再用加、减号连接，然后去括号，合并同类项．
一、选择题(共10题；每题2分，共20分)
1．（2分）（2023七上·龙华期末）某种商品进价为a元，在销售旺季，提价30%销售，旺季过后，商品以7折价格开展促销活动，这时一件商品的售价为（ ）
A．aB．0.7aC．1.03aD．0.91a
【答案】D
【规范解答】解：这时商品的售价为（元），
故答案为：D.
【思路点拨】由题意可得：售价为(1+30%)a，然后乘以70%可得打折后的售价.
2．（2分）（2023七上·苍南期末）图1是由3个相同小长方形拼成的图形其周长为24，图2中的长方形内放置10个相同的小长方形，则长方形的周长为（ ）
A．B．C．D．
【答案】C
【规范解答】解：设小长方形的长为x，宽为y，
由图1得：，
∴，
由图2得：长方形ABCD的长AB表示为：，宽AD表示为，
∴周长为：
故答案为：C.
【思路点拨】设小长方形的长为x，宽为y，利用平移的思想，结合图1可得4x+4y=24，即x+y=6；结合图2，用含x、y的式子表示出AB、AD、进而根据矩形的周长计算方法列出式子，根据整式加减法化简后再整体代入计算即可.
3．（2分）（2023七上·洛川期末）已知，，则代数式的值为
A．38B．35C．-35D．-32
【答案】C
【规范解答】解：
，
当，时，
原式
.
故答案为：C.
【思路点拨】根据去括号、合并同类项法则即可将代数式变形为-3(4m-3n)-2(x+2y)+3，然后将已知条件代入进行计算.
4．（2分）（2022七上·赵县期末）嘉琪在进行解方程的思维训练，其中有一个方程“2y-=y+■”中的■没印清晰，嘉琪问老师，老师只是说：“■是一个有理数，该方程的解与当×= 2时代数式5(x-1)-2(x- 2)-4的值相同．”嘉琪很快补上了这个有理数．你认为嘉琪补的这个有理数是（ ）
A．1B．-1C．2D．-2
【答案】A
【规范解答】当x＝2时代数式5（x﹣1）﹣2（x﹣2）﹣4
＝5x﹣5﹣2x+4﹣4
＝3x﹣5
＝3×2﹣5
＝1，
即y＝1，
代入方程中，即可得出补的这个有理数是1
故答案为：A
【思路点拨】先去括号，再合并同类项，得到化简后的结果，再把a＝1，b＝﹣2代入化简后的代数式进行计算即可．
5．（2分）（2023七上·洛川期末）已知x+2y＝7，4m﹣3n＝8，则代数式（9n﹣4y）﹣2（6m+x）+3的值为（ ）
A．38B．35C．﹣35D．﹣32
【答案】C
【规范解答】解：∵x+2y＝7，4m-3n＝8，
∴ (9n-4y)-2(6m+x)+3=9n-4y-12m-2x+3=-2(x+2y)-3(4m-3n)+3=-2×7-3×8+3=-14-24+3=-35.
故答案为：C.
【思路点拨】待求式可变形为-2(x+2y)-3(4m-3n)+3，然后将已知条件代入进行计算.
6．（2分）（2023七上·澄城期末）下面四个整式中，不能表示图中阴影部分面积的是（ ）
A．B．
C．D．
【答案】C
【规范解答】解：阴影部分的面积可以表示为：（x+3）（x+2）-2x=x2+3x+6，故A不符合题意；
或表示为x（x+3）+2×3=x（x+3）+6，故B不符合题意；
或表示出为3（x+2）+x2，故D不符合题意；
∵x2+3x+6≠x2+5x，故C符合题意；
故答案为：C
【思路点拨】利用图形中的数据，可知阴影部分的面积可表示为（x+3）（x+2）-2x=x（x+3）+2×3=3（x+2）+x2，据此可得到不符合题意的选项.
7．（2分）（2022七上·南宁月考）按如图所示的运算程序，若开始输入x的值为343，则第2022次输出的结果为（ ）
A．343B．1C．7D．49
【答案】C
【规范解答】解：由图所示的运算程序可知：
第1次输入x＝343≠1，输出49，
第2次输入x＝49≠1，输出7，
第3次输入x＝7≠1，输出1，
第4次输入x＝1，输出7，
第5次输入x＝7≠1，输出1，
第6次输入x＝1，输出7，
∴第2022次输出为7，
故答案为：C．
【思路点拨】根据给定的运算程序从输入343开始，找出输出的规律，即可确定第2022次输出的结果．
8．（2分）（2021七上·奉化期末）已知长方形ABCD， ， ，将两张边长分别为a和b（ ）的正方形纸片按图1，图2两种方式放置（图1，图2中两张正方形纸片均有部分重叠），矩形中未被这两张正方形纸片覆盖的部分用阴影表示，设图1中阴影部分的面积为 ，图2中阴影部分的面积为 ．当 时，AB的值是（ ）
A．7B．8C．9D．10
【答案】A
【规范解答】解：S1=（AB-a）•a+（CD-b）（AD-a）=（AB-a）•a+（AB-b）（AD-a），
S2=AB（AD-a）+（a-b）（AB-a），
∴S2-S1=AB（AD-a）+（a-b）（AB-a）-（AB-a）•a-（AB-b）（AD-a）
=（AD-a）（AB-AB+b）+（AB-a）（a-b-a）
=b•AD-ab-b•AB+ab
=b（AD-AB），
∵S2-S1=3b，AD=10，
∴b（10-AB）=3b，
∴AB=7．
故选：A．
【思路点拨】利用面积的和差关系，分别表示出S1和S2，再表示出S2-S1=b（AD-AB），结合S2-S1=3b，AD=10即可求解.
9．（2分）（2021七上·普宁期中）如图所示，在这个数据运算程序中，如果开始输入的x的值为10，那么第1次输出的结果是5，返回进行第二次运算，那么第2次输出的结果是16，……以此类推，第204次输出的结果是（ ）
A．1B．2C．4D．5
【答案】A
【规范解答】解：由数据运算程序得，如果开始输入的x的值为10，那么：
第1次输出的结果是5
第2次输出的结果是16
第3次输出的结果是8
第4次输出的结果是4
第5次输出的结果是2
第6次输出的结果是1
第7次输出的结果是4
……
综上可得，从第4次开始，每三个一循环
由 可得第204次输出的结果与第6次输出的结果相等
故答案为：A
【思路点拨】先找出规律：从第4次开始，每三个一循环，进行计算求解即可。
10．（2分）（2022·宁波模拟）将四张边长各不相同的正方形纸片按如图方式放入矩形 内（相邻纸片之间互不重叠也无缝隙），未被四张正方形纸片覆盖的部分用阴影表示.设右上角与左下角阴影部分的周长的差为 .若知道 的值，则不需测量就能知道周长的正方形的标号为（ ）
A．①B．②C．③D．④
【答案】D
【规范解答】解：设①、②、③、④四个正方形的边长分别为a、b、c、d，
由题意得,（a+d−b−c+b+a+d−b+b−c+c+c）−（a−d+a−d+d+d）=l，
整理得，2d=l，
则知道l的值，则不需测量就能知道正方形④的周长，
故答案为：D.
【思路点拨】设①、②、③、④四个正方形的边长分别为a、b、c、d，右上角阴影部分的周长 =a+d−b−c+b+a+d−b+b−c+c+c，左下角阴影部分的周长=a−d+a−d+d+d，根据两阴影周长差为l建立方程，求解即可.
二、填空题(共10题；每题2分，共20分)
11．（2分）（2023七上·杭州期末）单项式的系数是 ；次数是 .
【答案】；3
【规范解答】解：①由题意可知单项式的系数为，
故答案为：.
②由题意可知单项式的次数为
故答案为：3.
【思路点拨】单项式的次数：所有字母的指数之和叫做这个单项式的次数；单项式的系数：单项式中的数字因数叫做这个单项式的系数.
12．（2分）（2023七上·江北期末）若，则的值是 .
【答案】0
【规范解答】解：∵，
∴
，
故答案为：0.
【思路点拨】利用添括号法则，将待求式子含字母的部分放到一个前面带负号的括号内，进而整体代入计算即可.
13．（2分）（2023七上·兰溪期末）如图所示，一块砖的外墙面积为x，那么图中残缺墙面的面积为 .
【答案】
【规范解答】解：图中残缺墙面的面积为
故答案为：.
【思路点拨】由图形可得：残缺墙面的面积=三块砖的外墙面积+半块砖的外墙面积，然后结合一块砖的外墙面积为x进行解答.
14．（2分）（2023七上·慈溪期末）已知，，则 .
【答案】3
【规范解答】解：∵，，
∴
.
故答案为：3.
【思路点拨】待求式可变形为2(x2+2xy)-(y2+xy)，据此进行计算.
15．（2分）（2023七上·义乌期末）有一个长方体水箱，从里面量得它的深度为，底面长为，宽为，水箱里已盛有深度为的水.若往水箱里放入一个棱长为的立方体铁块，则水箱的水深为 .
【答案】10或30或a+2或1.25a
【规范解答】解：当放入立方体铁块后，水面刚好与立方体铁块相平时，由题意，得
，
∴，
∴水深为10cm；
当放入立方体铁块后，水面刚好与水箱顶部相平时，由题意，得
，
∴；
∴当时，水深为30cm；
当时，设此时水深为，由题意，得，
∴；
当时，设此时水深为，由题意，得，
∴，
综上所述，水箱的水深为30或a+2或1.25a.
故答案为：10或30或a+2或1.25a.
【思路点拨】分类讨论：①当放入立方体铁块后，水面刚好与立方体铁块相平时，根据水箱的长×宽×铁块的棱长=水箱原来水的体积+放入的立方体铁块的体积建立方程，求解可得a的值；②当放入立方体铁块后，水面刚好与水箱顶部相平时根据水箱的长×宽×铁块的棱长=水箱原来水的体积+放入的立方体铁块的体积建立方程，求解可得a的值；根据水箱容积=水箱原来水的体积+放入的立方体铁块的体积建立方程，求解可得a的值，当a≥28时，水深30cm，③当8≤a≤28时，设此时水深为xcm，根据根据水箱的长×宽×现在水的深度=水箱原来水的体积+放入的立方体铁块的体积建立方程，求解可表示出x；④当a＜8时，设此时水深为ycm，根据现在铁块没入水的体积+原来水箱中水的体积=水箱的长×宽×现在液面的高度建立方程，求解可表示出y，综上即可得出答案.
16．（2分）（2021七上·安吉期末）《孙子算经》是中国古代时期重要的数学专著，其中包含了“鸡兔同笼”“物不知数”等许多有趣的数学问题．《孙子算经》中记载：“今有物不知数，三三数之剩二，五五数之剩三，七七数之剩二，问物几何?”其译文为：“有一个正整数，除以3余2，除以5余3，除以7余2，求符合条件的正整数．”请用含k (k为自然数）的代数式表示满足条件的所有正整数 .
【答案】105k+23
【规范解答】解：∵一个正整数，除以3余2，除以7也余2
∴这个正整数除以21也余2
∵除以21余2的最小正整数是23
而
∴满足条件的最小正整数为23
∵3、5、7的最小公倍数为3×5×7=105
∴满足条件的所有正整数 可以表示为： 105k+23
故答案为： 105k+23。
【思路点拨】根据余同先求出除以21余2的最小正整数，再求出除以5余3的最小正整数，最后利用最小公倍数将所有正整数用代数式表示出来。
17．（2分）（2021七上·深圳期中）数学真奇妙：两个有理数a和b，如果分别计算a＋b，a﹣b，ab，的值，发现有三个结果恰好相同，则b＝ ．
【答案】-1
【规范解答】解：∵有意义，
∴b≠0，
∴a+b≠a﹣b，
∵a+b，a﹣b，ab，的值有三个结果恰好相同，
∴ab＝，
∴当a＝0，ab＝成立，
当a≠0时，即，
∴b＝±1，
当a＝0时，a+b＝b，a﹣b＝﹣b，ab＝0，＝0，
∴此时不能有三个结果恰好相同；
当b＝1时，a+b＝a+1，a﹣b＝a﹣1，ab＝a，＝a，
∴此时不能有三个结果恰好相同；
当b＝﹣1时，a+b＝a﹣1，a﹣b＝a+1，ab＝﹣a，＝﹣a，
∴a﹣1＝﹣a或a+1＝﹣a，
∴a＝或a＝；
∴能使三个结果恰好相同时，b的值为﹣1，
故答案为：﹣1．
【思路点拨】由题意可知a=0或b=±1，再分别对a、b的值进行讨论，可得b=-1，a=或a＝。
18．（2分）（2020七上·江夏月考）已知a、b、c是非零有理数，且a＋b＋c＝0，abc＜0，求 ＝ .
【答案】1或-1
【规范解答】解：∵a、b、c是非零有理数，且a＋b＋c＝0，abc＜0，
∴三个数中只有一个数是负数，
∴当 是异号时，则有 ，
当 是同号时，则有 ，
∴ 的值为1或-1；
故答案为：1或-1.
【思路点拨】根据题意易得a、b、c的正负可能是一负两正，然后进行分类求解即可.
19．（2分）（2020七上·海曙月考）下图是一个程序运算图，若开始输入的数是125，则2020次之后输出的数是 .
【答案】5
【规范解答】解：设n为输入的次数，
当n=1：输入125，∵x≠1，得125÷5=25，
当n=2：输入25，∵x≠1，得25÷5=5，
当n=3：输入5，∵x≠1，得5÷5=1，
当n=4：输入1，∵x=1，得4+1=5，
当n=5：输入5，∵x≠1，得5÷5=1，
当n=6：输入1，∵x=1，得4+1=5，
∴当n>4时，每两次一循环，第奇数次是1，第偶数次是5，
∴当n=2020时，输出的数是5.
故答案为：5.
【思路点拨】根据程序运算图，代入x的值，根据结果判断是否等于1，分别求出每次输出的数字，最后得出规律，当n>4时，每两次一循环，第奇数次是1，第偶数次是5，从而推出当n=2020时，输出的数是5.
20．（2分）（2020七上·南浔期末）已知长方形ABCD，AD>AB，AD=10，将两张边长分别为a和b（a>b） 的正方形纸片按图1，图2两种方式放置（图1，图2中两张正方形纸片均有部分重叠），矩形中未被这两张正方形纸片覆盖的部分用阴影表示，设图1中阴影部分的面积为S1，图2中阴影部分的面积为S2，当S2-S1=3b时，AB= 。
【答案】7
【规范解答】解：设AB=x,
则S1=10x-a2-b2+(a+b-10)b, S2=10x-a2-b2+(a+b-x)b,
∵S2-S1=3b ,
∴10x-a2-b2+(a+b-x)b-10x+a2+b2-(a+b-10)b=3b,
-bx=-7b,
∴x=7.
故答案为：7.
【思路点拨】本题运用设而不求的思想，设AB=x, 分别吧两个阴影部分的面积用含a、b和x的代数式表示，代入给定的关系式，整理化简即可求值.
三、解答题(共8题；共61分)
21．（5分）（2022七上·利川期末）化简下列各式：
（1）（2分）；
（2）（3分）.
【答案】（1）解：
（2）解：
【思路点拨】（1）先去括号（括号前是负号，去掉括号和负号，括号里的每一项都要变号；括号前面是正号，去掉括号和正号，括号里的每一项都不变号，括号前的数要与括号里的每一项都要相乘），再合并同类项即可；
（2）先去括号（括号前是负号，去掉括号和负号，括号里的每一项都要变号；括号前面是正号，去掉括号和正号，括号里的每一项都不变号，括号前的数要与括号里的每一项都要相乘），再合并同类项化简即可.
22．（5分）（2022七上·昌邑期末）一块三角尺的形状和尺寸如图所示，如果圆孔的半径是r，三角尺的厚度是h，用式子表示这块三角尺的体积V．若，求V的值（取3）．
【答案】解：整个三角板的体积为，圆孔的体积为，
所以，所求三角板的体积，
若a=6cm，r=0.5cm，h=0.2cm，把它们代入上式，得：
．
答：V的值是3.45cm3．
【思路点拨】 利用这块三角尺的体积=三棱柱的体积-圆孔（圆柱）的体积，进行计算即可.
23．（5分）（2022七上·丰满期末）历史上的数学巨人欧拉最先把关于x的多项式用记号来表示，把x等于某数m时的多项式的值用来表示．例如，对于多项式，当时，多项式的值为，若，求的值．
【答案】解：∵，，
∴，即，
∴，
即．
【思路点拨】将x=-1代入多项式可得，再将x=1代入多项式可得， 然后整体代入计算即可.
24．（8分）（2020七上·高平期中）某电器商销售一种微波炉和电磁炉，微波炉每台定价800元，电磁炉每台定价200元．“双十一”期间商场决定开展促销活动，活动期间向客户提供两种优惠方案．
方案一：买一台微波炉送一台电磁炉；方案二：微波炉和电磁炉都按定价的90%付款．
现某客户要到该卖场购买微波炉2台，电磁炉x台（x＞2）．
（1）（4分）若该客户按方案一购买，需付款 元．（用含x的代数式表示）；若该客户按方案二购买，需付款 元．（用含x的代数式表示）
（2）（2分）若x＝5时，通过计算说明此时按哪种方案购买较为合算？
（3）（2分）当x＝5时，你能给出一种更为省钱的购买方案吗？试写出你的购买方法．
【答案】（1）200x＋1200；180x＋1440
（2）解：将x＝5代入方案一的付款中得：200×5＋1200＝2200元，
x＝5代入方案二的付款中得：180×5＋1440＝2340元，
∵2200元＜2340元，
∴当x＝5时，按方案一购买比较合算。
（3）解：若该客户按方案一购买微波炉2台送电磁炉2台；再按方案二购买电磁炉3台．
付款金额为：800×2＋200×3×90%＝2140元．
∵2140元＜2200元，
∴当x＝5时，按此方案购买更为省钱．
【规范解答】解：（1）根据题意：若该客户按方案一购买，需付款：800×2＋200（x－2）＝200x＋1200元；
若该客户按方案二购买，需付款：90%×（800×2＋200x）＝180x＋1440元；
故答案为：200x＋1200；180x＋1440．
【思路点拨】（1）根据题目提供的两种不同的付款方式列出代数式即可；
（2）将x=5分别代入（1）中两个代数式分别求出费用，然后比较即可；
（3）根据题意考虑可以先按方案一购买微波炉2台送电磁炉2台；再按方案二购买电磁炉3台的费用，然后与（2）中的结论比较即得.
25．（8分）（2023七上·龙华期末）甲、乙两家超市以相同的价格出售同样的商品，但为了吸引顾客，各自推出不同的优惠方案.在甲超市累计购买商品超过400元后，超出的部分按原价收取：在乙超市购买商品只按原价的收取.设某顾客预计累计购物x元.
（1）（4分）当时，分别用代数式表示顾客在两家超市购物所付的费用；
（2）（4分）当时，该顾客应选择哪一家超市购物比较合算?说明理由.
【答案】（1）解：当时，由题意可知，
在甲超市购物所付费用为：，
在乙超市购物所付费用为：；
（2）解：当x=1000元时，在甲超市购物所付费用：(元)，
在乙超市购物所付费用为：(元)，
∵820元800元，
∴顾客应选择乙超市购物比较合算.
【思路点拨】（1）当x>400时，根据400+超过400元的部分的费用即可表示出在甲超市购买的费用；根据原价×80%可得在乙超市购买的费用；
（2）将x=1000代入（1）的关系式中求出相应的值，然后进行比较即可判断.
26．（8分）（2023七上·武义期末）如图，两叠规格相同的杯子整齐地叠放在桌面上，请根据图中给出的数据信息，解答下列问题：
（1）（4分）按如图所示叠放一起时，相邻两个杯子杯口之间的高度相差 cm.
（2）（4分）若x个杯子按如图所示整齐叠放在桌面上，求这些杯子的顶部距离桌面的距离（用含x的代数式表示）.当时，求这些杯子的顶部距离桌面的距离.
【答案】（1）2
（2）解：一个杯子的高度为：cm，
每增加一个杯子，所叠杯子的总高度增加，
故杯子的顶部距离桌面的距离为：，
将代入中得：（cm），
故这些杯子的顶部距离桌面的距离为.
【规范解答】解：（1）（cm），
故相邻两个杯子杯口之间的高度相差；
故答案为：2；
【思路点拨】（1）观察发现，两个杯子整齐地叠放在一起高10cm，三个杯子整齐地叠放在一起高12cm，故作差即可得出相邻两个杯子杯口之间的高度；
（2）由（1）的计算结果，首先求出 一个杯子的高度，进而用一个杯子的高度加上x个杯子叠放在一起增加的高度即可求出杯子的顶部距离桌面的距离；最后将x=10代入所所得的式子计算即可.
27．（12分）（2023七上·成都期末）已知是最小的正整数，，满足，且，，分别对应数轴上的点，，．
（1）（4分）请直接写出，，的值： ， ， ．
（2）（3分）若点为一动点，从点出发以每秒2个单位长度的速度向右运动，则点运动几秒后，点到点的距离是点到点的距离的2倍？
（3）（5分）点以每秒1个单位长度的速度向左运动，同时点和点分别以每秒2个单位长度和5个单位长度的速度向右运动．点与点之间的距离表示为，点与点之间的距离表示为假设运动时间为，的值是否随着时间的变化而改变？若变化，请说明理由；若不变，请求其值．
【答案】（1）-1；1；5
（2）解：设点P运动x秒后，点P到点A的距离是点P到点C的距离的2倍，
∴PA=2x，
∵点A，C表示的数分别为-1，5，
∴AC=5-（-1）=6
当点P在点A、C之间时，PC=6-2x，
2x=2（6-2x），
解之：x=2；
当点P在点C的右边时，PC=2x-6，
2x=2（2x-6）
解之：x=6.
∴点P运动2秒或6秒后，点P到点A的距离是点P到点C的距离的2倍
（3）解：由题意得，运动后，点A表示的数为-1-t，点B表示的数是1+2t，点C表示的数是5+5t，
∴AB=1+2t-（-1-t）=3t+2，
BC=5+5t-（1+2t）=3t+4，
∴BC-AB=3t+4-（3t+2）=2，
∴BC-AB的值是定值，BC-AB的值不随着时间t的变化而变化，其值为2.
【规范解答】解：（1）∵（c-5）2+|a+b|=0，
∴c-5=0且a+b=0
∴c=5，a+b=0，
∵b是最小的正整数，
∴b=1，
∴a=-1.
故答案为：-1，1，5
【思路点拨】（1）利用几个非负数之和为0，则每一个数都为0，可得到关于a，b，c的方程组，再根据最小的正整数是1，可得到b的值，从而可求出a，b，c的值.
（2）设点P运动x秒后，点P到点A的距离是点P到点C的距离的2倍，可表示出PA的长，利用点A，C所表示的数，可得到AC的长；再分情况讨论：当点P在点A、C之间时，PC=6-2x；当点P在点C的右边时，PC=2x-6；分别根据PA=2PC，可得到关于x的方程，解方程求出x的值.
（3）利用点A，B的运动速度和方向，可得到运动t秒后，点A，B，C表示的数，再用含t的代数式分别表示出AB，BC的长，再求出BC-AB的值，根据其值可作出判断.
28．（10分）（2022七上·大田期中）如图
（1）（3分）【操作感知】如图①，长方形透明纸上有一条数轴，是周长为4的圆的直径，点与数轴原点重合，将圆从原点出发沿数轴正方向滚动1周，点落在数轴上的点处；将圆从原点出发沿数轴负方向滚动半周，点落在数轴上的点处，折叠长方形透明纸，使数轴上的点与点重合，此时折痕与数轴交点表示的数为 .
（2）（2分）【建立模型】折叠长方形透明纸，使得数轴上表示数的点与表示数的点重合，则折痕与数轴交点表示的数为 （用含，的代数式表示）.
（3）（2分）【问题解决】若，，为数轴上不同的三点，点表示的数为，点表示的数为-2，如果，，三点中的一点到其余两点的距离相等，求点表示的数；
（4）（3分）如图②，若是周长为的圆的直径，点与数轴原点重合，将圆从原点出发沿数轴正方向滚动2周，点落在数轴上的点处；将圆从原点出发沿数轴负方向滚动周，点落在数轴上的点处.将此长方形透明纸沿，剪开，将点，之间一段透明纸对折，使其左、右两端重合，这样连续对折次后，再将其展开，求最右端折痕与数轴交点表示的数.
【答案】（1）1
（2）
（3）解：设点表示的数是，
当到、距离相等，即是中点时，，
当到、距离相等，即是中点时，，解得，
当到、距离相等，即是中点时，，解得，
综上所述，点E表示的数为1或10或-8；
（4）解：由已知得表示的数是，表示的是-3，
∴、间的距离为9，
而对折次后，每两条相邻折痕间的距离相等，这个距离是，
∴最右端的折痕与数轴的交点表示的数为.
【规范解答】解：（1）【操作感知】由题意可知，A'表示的数是4，B'表示的数是-2，
∵折叠长方形透明纸，使数轴上的点A'与点B'重合，
∴A'与点B'关于折痕对称，即A'B'中点为折痕与数轴的交点，
而A'B'中点表示的数为，
故答案为：1；
（2）【建立模型】∵MN关于折痕对称，
∴MN的中点即是折痕与数轴交点，
而MN的中点表示的数是，
∴折痕与数轴交点表示的数为，
故答案为：；
【思路点拨】（1）由已知得出A'、B'表示的数，再求出A'B'中点即可得答案；
（2）求出MN的中点表示的数即可得到答案；
（3）分三种情况：① 当E到C、D距离相等，即E是CD中点时，②当C到E、D距离相等，即C是ED中点时 ，③ 当D到C、E距离相等，即D是CE中点时， 分别列出方程，即可得答案；
（4）先求出PQ的长度，再根据每两条相邻折痕间的距离为 ，即可得最右端的折痕与数轴的交点表示的数．