2024-2025学年湖南省郴州市永兴县树德初级中学八年级（上）入学数学试卷（含解析）

这是一份2024-2025学年湖南省郴州市永兴县树德初级中学八年级（上）入学数学试卷（含解析），共18页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题：本题共10小题，共30分。
1.下列图形中，是轴对称图形的是( )
A. B. C. D.
2.若x=3y=−2是关于x，y的二元一次方程2k=3x+4y+5的一个解，则k的值是( )
A. 3B. 4C. 5D. 6
3.下列运算正确的是( )
A. (3x)3=9x3B. (x−2)2=x2−4
C. (−2ab2)2=4a2b4D. 3a+4b=7ab
4.以下因式分解正确的是( )
A. ax2−a=a(x2−1)B. m3+m=m(m2+1)
C. x2+2x−3=x(x+2)−3D. x2+2x−3=(x−3)(x+1)
5.下列各式中，能用完全平方公式分解因式的是( )
A. 16x2+1B. x2+2x−1C. a2+2ab+4b2D. x2−x+14，
6.下列说法正确的是( )
A. 同一平面内，垂直于同一条直线的两条直线平行
B. 在同一平面内过一点有且只有一条直线与已知直线垂直
C. 如果两个角相等，那么这两个角是对顶角
D. 连接直线外一点与直线上各点的所有线段中，垂线段最短
7.如图，直线l1和l2被直线l3和l4所截，∠1=∠2=130°，∠3=75°，则∠4的度数为( )
A. 75°
B. 105°
C. 115°
D. 130°
8.某班15名男生引体向上成绩如表，则这组数据的众数和中位数分别是( )
A. 7，10B. 10，7C. 10，10D. 7，12
9.《孙子算经》是我国古代著名的数学典籍，其中有一道题：“今有木，不知长短.引绳度之，余绳四尺五寸；屈绳度之，不足一尺.木长几何？”意思是：用一根绳子去量一根长木，绳子还剩余4.5尺；将绳子对折再量长木，长木还剩余1尺.问木长多少尺？设木长x尺，绳子长y尺，则可以列出的方程组为( )
A. y−x=4.5x−0.5y=1B. y−x=4.5x+0.5y=1C. x+y=4.5x−y=1D. x+y=4.5y−x=1
10.图(1)是一个长为2a，宽为2b(a>b)的长方形，用剪刀沿图中虚线(对称轴)剪开，把它分成四块形状和大小都一样的小长方形，然后按图(2)那样拼成一个正方形，则中间空的部分的面积是( )
A. abB. (a+b)2C. (a−b)2D. a2−b2
二、填空题：本题共8小题，每小题3分，共24分。
11.计算82024×(−0.125)2025= ______．
12.分解因式：2m2−8= ．
13.已知3x−2y=1，用含y的代数式表示x，则x= ______．
14.已知xy=2，x−y=−4，则x2+xy+y2=______．
15.若方程组3x−2y=4k−52x−3y=k的解满足x+y=10，则k等于______．
16.折纸是一门古老而有趣的艺术，现代数学家们甚至为折纸建立了一套完整的“折纸几何学公理”.如图，小明在课余时间把一张长方形纸片ABCD沿EF折叠，∠1=65°，则∠2= ______．
17.如图，两个全等的直角三角形重叠在一起，将其中的一个三角形沿着
点B到C的方向平移到△DEF的位置，AB=10，DO=3，平移距离为6，
则阴影部分面积为______．
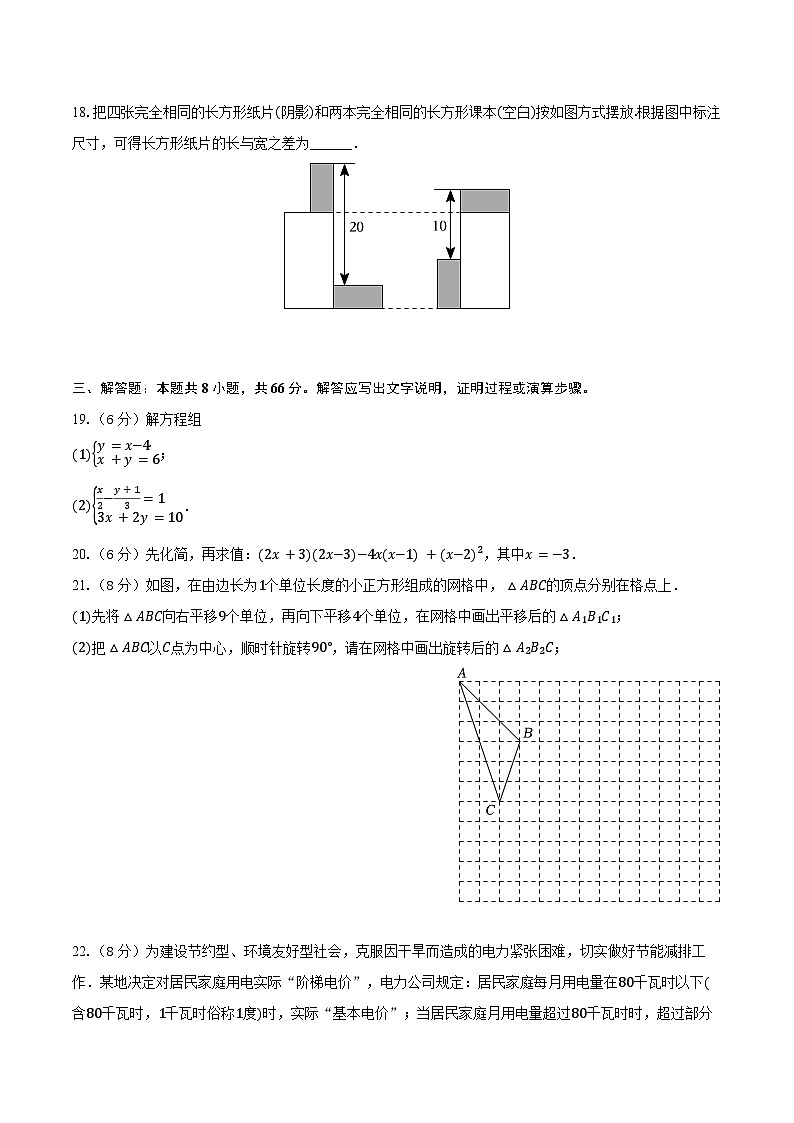
18.把四张完全相同的长方形纸片(阴影)和两本完全相同的长方形课本(空白)按如图方式摆放.根据图中标注尺寸，可得长方形纸片的长与宽之差为______．
三、解答题：本题共8小题，共66分。解答应写出文字说明，证明过程或演算步骤。
19.（6分）解方程组
(1)y=x−4x+y=6；
(2)x2−y+13=13x+2y=10．
20.（6分）先化简，再求值：(2x+3)(2x−3)−4x(x−1)+(x−2)2，其中x=−3．
21.（8分）如图，在由边长为1个单位长度的小正方形组成的网格中，△ABC的顶点分别在格点上．
(1)先将△ABC向右平移9个单位，再向下平移4个单位，在网格中画出平移后的△A1B1C1；
(2)把△ABC以C点为中心，顺时针旋转90°，请在网格中画出旋转后的△A2B2C；
22.（8分）为建设节约型、环境友好型社会，克服因干旱而造成的电力紧张困难，切实做好节能减排工作．某地决定对居民家庭用电实际“阶梯电价”，电力公司规定：居民家庭每月用电量在80千瓦时以下(含80千瓦时，1千瓦时俗称1度)时，实际“基本电价”；当居民家庭月用电量超过80千瓦时时，超过部分实行“提高电价”．
(1)小张家2011年4月份用电100千瓦时，上缴电费68元；5月份用电120千瓦时，上缴电费88元．求“基本电价”和“提高电价”分别为多少元/千瓦时？
(2)若6月份小张家预计用电130千瓦时，请预算小张家6月份应上缴的电费．
23.（8分）如图，点F在线段AB上，点E，G在线段CD上，FG//AE，∠1=∠2．
(1)求证：AB//CD；
(2)若FG⊥BC于点H，BC平分∠ABD，∠D=112°，求∠1的度数．
24.（8分）某校七、八年级开展了“国学朗诵”活动，对学生的活动情况按10分制进行评分，成绩(单位：分)均为不低于6的整数.为了解这次活动的效果，现从这两个年级各随机抽取10名学生的活动成绩作为样本进行整理，并绘制统计图表，部分信息如下：
七年级10名学生活动成绩统计表
八年级10名学生活动成绩扇形统计图

已知七年级10名学生活动成绩的中位数为8.5分.请根据以上信息，完成下列问题：
(1)a= ______，b= ______；
(2)样本中，八年级活动成绩的众数为______分；
(3)若认定比赛成绩不低于9分为“优秀”，根据样本数据，判断本次活动中优秀率高的年级是否平均成绩也高，并说明理由．
25.（10分）数学活动课上，老师准备了若干个如图1的三种纸片，A种纸片是边长为a的正方形，B种纸片是边长为b的正方形，C种纸片是长为b、宽为a的长方形，并用A种纸片一张，B种纸片一张，C种纸片两张拼成如图2的大正方形．
(1)观察图2，请你写出下列三个代数式：(a+b)2，a2+b2，ab之间的等量关系．
(2)若要拼出一个面积为(a+2b)(a+b)的矩形，则需要A号卡片1张，B号卡片2张，C号卡片______张.
(3)根据(1)题中的等量关系，解决如下问题：
①已知：a+b=5，a2+b2=11，求ab的值；
②已知(x−2021)2+(x−2023)2=20，求x−2022的值．
26.（12分）如图，直线PQ//MN，一副三角板(∠ABC=∠CDE=90°,∠ACB=30°,∠BAC=60°,∠DCE=∠DEC=45°)按如图①放置，其中点E在直线PQ上，点B，C均在直线MN上，且CE平分∠ACN．

(1)求∠DEQ的度数；
(2)如图②，若将△ABC绕B点以每秒10°的速度按逆时针方向旋转(A、C的对应点分别为F、G).设旋转时间为t秒(0≤t≤36)；
①在旋转过程中，若边BG//CD，求t的值；
②若在△ABC绕B点旋转的同时，△CDE绕E点以每秒5°的速度按顺时针方向旋转(C、D的对应点分别为K、T)，请直接写出EK与BG平行时t的值．
答案解析
1.D
【解析】解：选项A、B、C的图形均不能找到这样的一条直线，使直线两旁的部分能够完全重合，所以不是轴对称图形，不符合题意；
选项D的图形能找到这样的一条直线，使直线两旁的部分能够完全重合，所以是轴对称图形，符合题意．
故选：D．
根据轴对称图形的概念逐项分析判断即可，轴对称图形的概念：平面内，一个图形沿一条直线折叠，直线两旁的部分能够完全重合的图形．
本题考查轴对称图形，关键是掌握轴对称图形的定义．
2.A
【解析】解：将x=3y=−2代入关于x，y的二元一次方程2k=3x+4y+5中，得
2k=3×3+4×(−2)+5，
解得k=3，
故选：A．
将x=3y=−2代入关于x，y的二元一次方程2k=3x+4y+5中即可求出k的值．
本题考查了二元一次方程的解，熟知方程的解的定义是解题的关键．
3.C
【解析】解：(3x)3=33x3=27x3，故A不正确；
(x−2)2=x2−4x+4，故B不正确；
(−2ab2)2=(−2)2a2(b2)2=4a2b4，故C正确；
3a+4b中3a和4b不能合并同类项，故D不正确．
故选：C．
根据积的乘方，完全平方公式以及合并同类项的方法逐个进行计算后即可选出正确答案．
本题主要考查完全平方公式，积的乘方等知识点，熟练掌握完全平方公式和积的乘方的运算法则是解决问题的关键．
4.B
【解析】解：(A)ax2−a=a(x2−1)=a(x+1)(x−1)；
故A不正确，不符合题意．
(B)m3+m=m(m2+1)；
故B正确，符合题意．
(C)x2+2x−3=(x+3)(x−1)；
故CD不正确，不符合题意．
故选：B．
利用平方差公式，x2−1还可分解因式；利用十字相乘法，x2+2x−3=(x+3)(x−1)．
本题考查因式分解，灵活掌握因式分解的方法是本题的关键．
5.D
【解析】解：A、16x2+1只有两项，不符合完全平方公式；
B、x2+2x−1其中有两项x2、−1不能写成平方和的形式，不符合完全平方公式；
C、a2+2ab+4b2另一项不是a、2b的积的2倍，不符合完全平方公式；
D、x2−x+14符合完全平方公式．
故选：D．
根据完全平方公式的结构特点：必须是三项式，其中有两项能写成两个数(或式)的平方和的形式，另一项是这两个数(或式)的积的2倍，对各选项分析判断后利用排除法求解．
本题主要考查了完全平方公式，熟记公式结构是解题的关键．完全平方公式：a2±2ab+b2=(a±b)2；
6.ABD
【解析】解：A，根据同一平面内两条直线的位置关系可知，在同一平面内，垂直于同一条直线的两条直线互相平行的说法是正确的，选项A符合题意；
B，在同一平面内，过一点有且只有一条直线与已知直线垂直，选项B符合题意；
C，如果两个角相等，那么这两个角是对顶角，说法错误，也可能是同位角，选项C不符合题意；
D，根据垂直的性质：从直线外一点与直线上各点连接而得到的所有线段中，垂线段最短，选项D符合题意；
故选：ABD．
A.根据同一平面内两条直线的位置关系可知，可判断出A是否正确；
B.在同一平面内，过一点有且只有一条直线与已知直线垂直，可判断出B是否正确；
C.如果两个角相等，那么这两个角是对顶角，说法错误，也可能是同位角，可判断出C是否正确；
D.根据垂直的性质，可判断出D是否正确．
本题主要考查了平行线的性质、同位角、对顶角、垂线最短等知识点，解题关键是熟悉相关的定义和判定方法．
7.B
【解析】解：
∵∠1=∠2=130°，
∴l1//l2，
∴∠5=∠3=75°，
∵∠5+∠4=180°，
∴∠4=180°−∠5
=180°−75°
=105°，
故选：B．
利用“同位角相等，两直线平行”得l1//l2，再利用“两直线平行，同位角相等”得∠5=∠3，最后由∠5和∠4互为补角，从而求出∠4得度数．
本题考查的是平行线的判定与性质、余角和补角，掌握平行线的判定和性质是解题的关键．
8.A
【解析】解：15名男生引体向上成绩出现次数最多的是7个，共出现5次，因此众数是7，
将这15名男生引体向上成绩从小到大排列，处在中间位置的一个数是10个，因此中位数是10，
故选：A．
根据众数、中位数的定义进行判断即可．
本题考查中位数、众数，理解“在一组数据中出现次数最多的数是众数，将一组数据从小到大排列后，处在中间位置的一个数或两个数的平均数是中位数”是正确解答的关键．
9.A
【解析】解：∵用绳子去量长木，绳子还剩余4.5尺，
∴y−x=4.5；
∵将绳子对折再量长木，长木还剩余1尺，
∴x−0.5y=1．
∴根据题意可列方程组y−x=4.5x−0.5y=1．
故选：A．
根据“用绳子去量长木，绳子还剩余4.5尺；将绳子对折再量长木，长木还剩余1尺”，即可列出关于x，y的二元一次方程组，此题得解．
本题考查了由实际问题抽象出二元一次方程组，找准等量关系，正确列出二元一次方程组是解题的关键．
10.C
【解析】解：∵图(1)是一个长为2a，宽为2b(a>b)的长方形，
∴正方形的边长为：a+b，
∵由题意可得，正方形的边长为(a+b)，
∴正方形的面积为(a+b)2，
∵原矩形的面积为2a⨉2b=4ab，
∴中间空的部分的面积
=(a+b)2−4ab=(a−b)2．
故选：C．
先求出正方形的边长，继而得出面积，然后根据空白部分的面积=正方形的面积−矩形的面积即可得出
此题考查了完全平方公式的几何背景，求出正方形的边长是解答本题的关键．
11.−0.125
【解析】解：82024×(−0.125)2025
=82024×(−0.125)2024×(−0.125)
=(8×0.125)2024×(−0.125)
=1×(−0.125)
=−0.125；
故答案为：−0.125．
利用积的乘方的逆用进行计算即可．
本题考查幂的乘方与积的乘方，熟练掌握运算法则是解题的关键．
12.2(m+2)(m−2)
【解析】解：2m2−8，
=2(m2−4)，
=2(m+2)(m−2)．
故答案为2(m+2)(m−2)．
13.2y+13
【解析】解：3x−2y=1，
3x=2y+1，
x=2y+13，
故答案为：2y+13．
将y看作已知数求出x．
本题考查了解二元一次方程，解题的关键是将y看作已知数求出x．
14.22
【解析】解：∵(x−y)2=x2−2xy+y2，
∴x2+y2=(x−y)2+2xy，
∵xy=2，x−y=−4，
∴x2+y2=20，
∴x2+xy+y2=20+2=22．
故答案为：22．
根据完全平方公式：(a±b)2=a2±2ab+b2，解答即可．
此题考查了完全平方公式，熟记完全平方公式是解题的关键．
15.5
【解析】解：3x−2y=4k−5①2x−3y=k②，
①−②得x+y=3k−5，
∵x+y=10，
∴3k−5=10，
∴k=5．
故答案为：5．
运用整体思想直接将两个方程相减可得x+y=3k−5，再结合条件x+y=10即可求出k．
本题考查了二元一次方程组的解，掌握用整体思想解二元一次方程组的方法是关键．
16.50°
【解析】解：由题意可知∠1=∠FEG=65°，
∵∠1+∠FEG+∠2=180°，
∴∠2=50°，
故答案为：50°．
由题意可知∠1=∠FEG，再根据平角的定义即可求出∠2的度数．
本题考查的是轴对称的性质，平行线的性质，掌握轴对称的性质是解题的关键．
17.51
【解析】解：由平移的性质知，BE=6，DE=AB=10，
∴OE=DE−DO=10−3=7，
∵△ABC≌△DEF，
∴S△ABC=S△DEF，
∴S四边形ODFC=S梯形ABEO=12(AB+OE)⋅BE=12×(10+7)×6=51，
故答案为：51．
根据平移的性质分别求出BE、DE，根据题意求出OE，根据全等三角形的性质、梯形的面积公式计算，得到答案．
本题考查的是全等三角形的性质、平移的性质，掌握全等形的面积相等是解题的关键．
18.5
【解析】解：设小长方形的长为x，宽为y，
根据题意得：20+y−x=10+x−y，即2x−2y=20−10，
整理得：x−y=20−102=5，
小长方形的长与宽的差是5，
故答案为：5．
设小长方形的长为x，宽为y，根据题意列出方程，解方程即可得到结论．
此题考查了二元一次方程的应用，整式的加减，熟练掌握运算法则是解本题的关键．
19.解：(1)y=x−4①x+y=6②，
①代入②得x+x−4=6，
x=5，
把x=5代入得y=1，
∴x=5y=1；
(2)x2−y+13=1①3x+2y=10②，
由①得3x−2y−2=6，即3x−2y=8③，
②+③得到6x=18，
x=3，
把x=3代入得y=12，
∴x=3y=12．
【解析】(1)利用代入消元法解方程组即可；
(2)利用加减消元法解方程组即可．
本题考查解二元一次方程组，解题的关键是掌握解方程组的方法．
20.解：(2x+3)(2x−3)−4x(x−1)+(x−2)2，
=4x2−9−(4x2−4x)+x2−2x+4，
=4x2−9−4x2+4x+x2−4x+4，
=x2−5，
当x=3时，x2−5=32−5=9−5=4．
【解析】有括号，先算括号，展开式子，合并同类项，再计算求值．
本题考查了平方差公式、完全平方公式的综合应用，综合性较强，在计算过程中，要特别细心．
21.解：(1)分别将点A、B、C向右平移9个单位，再向下平移4个单位得到对应点A1、B1、C1，
连接各点，得平移后的△A1B1C1，如图所示：
(2)①利用网格特点，分别将CA、CB以C为中心顺时针旋转90°找出对应线段CA2、CB2，
连接A2B2，
得旋转后的△A2B2C，如图所示：
【解析】(1)分别将点A、B、C向右平移9个单位，再向下平移4个单位找出对应点A1、B1、C1即可；
(2)分别将CA、CB以C为中心顺时针旋转90°找出对应线段CA2、CB2即可．
本题考查了网格作图，熟练掌握平移作图、旋转作图，是解题的关键．
22.解：(1)设“基本电价”为x元/千瓦时，“提高电价”为y元/千瓦时，根据题意，得
80x+(100−80)y=6880x+(120−80)y=88
解之，得x=0.6y=1
答：“基本电价”为0.6元/千瓦时，“提高电价”为1元/千瓦时．
(2)80×0.6+(130−80)×1=98(元)．
答：预计小张家6月份上缴的电费为98元．
【解析】设“基本电价”和“提高电价”分别为x、y元/千瓦时，则根据4月份电费不变得出，80x+(100−80)y=68；由5月份电费不变得，80x+(120−80)y=88，列方程组求解．(2)由(1)得出的“基本电价”和“提高电价”求出6月份应上缴的电费．
此题考查的是二元一次方程组的应用，解题的关键是理解明确上缴电费的计算方法，列方程组求解．
23.(1)证明：∵FG//AE，
∴∠2=∠3，
∵∠1=∠2，
∴∠1=∠3，
∴AB//CD．
(2)解：∵AB//CD，
∴∠ABD+∠D=180°，
∵∠D=112°，
∴∠ABD=180°−∠D=68°，
∵BC平分∠ABD，
∴∠4=12∠ABD=34°，
∵FG⊥BC，
∴∠1+∠4=90°，
∴∠1=90°−34°=56°．
【解析】(1)欲证明AB//CD，只要证明∠1=∠CGF即可．
(2)根据∠1+∠4=90°，先求出∠4即可解决问题．
本题考查三角形内角和定理，平行线的性质，角平分线的定义等知识，解题的关键是熟练掌握基本知识．
24.2 2 8
【解析】解：(1)∵七年级10名学生活动成绩的中位数为8.5分，
∴第5名学生为8分，第6名学生为9分，
∴a=5−1−2=2，
b=10−2−1−2−3=2，
故答案为：2，2．
(2)根据扇形统计图，八年级活动成绩的众数为8分，
故答案为：8．
(3)优秀率高的年级不是平均成绩也高，理由如下，
根据扇形统计图，八年级活动成绩为7分的学生数的占比为1−40%−20%−20%=20%，
八年级优秀率为20%+20%=40%，平均成绩为：7×20%+8×40%+9×20%+10×20%=8.4，
七年级优秀率为3+210×100%=50%>40%，平均成绩为：110×(6×2+7+8×2+9×2+10×3)=8.3，
∴优秀率高的年级为七年级，但平均成绩八年级更高，
∴优秀率高的年级不是平均成绩也高．
(1)根据中位数的定义，得出第5名学生为8分，第6名学生为9分，进而求得a，b的值，即可求解；
(2)根据扇形统计图结合众数的定义，即可求解；
(3)分别求得七年级与八年级的优秀率与平均成绩，即可求解．
本题考查扇形统计图，中位数，众数，平均数，明确相关概念的定义，能从统计图中获取信息是解题的关键．
25.3
【解析】解：(1)大正方形的面积可以表示为：(a+b)2，或表示为：a2+b2+2ab；
因此有(a+b)2=a2+b2+2ab；
(2)根据题意得：(a+2b)(a+b)=a2+3ab+2b2，
则需要A号卡片1张，B号卡片2张，C号卡片3张．
故答案为：3；
(3)①∵(a+b)2=a2+b2+2ab，a+b=5，a2+b2=11，
∴25=11+2ab，
∴ab=7，即ab的值为7；
②令a=x−2022，
∴x−2021
=[x−(2022−1)]
=x−2022+1
=a+1，
x−2023
=[x−(2022+1)]
=x−2022−1
=a−1，
∵(x−2021)2+(x−2023)2=20，
∴(a+1)2+(a−1)2=20，
解得：a2=9．
∴(x−2022)2=9，
∴x−2022=±3．
(1)如图2，大正方形的面积直接求和间接求，得到等式即可；
(2)根据题意列出算式，利用多项式乘多项式法则计算，合并后即可作出判断；
(3)①利用完全平方公式列出关系式，把已知等式代入计算即可求出值ab的值；
②令x−2022=a，则有x−2023=a+1，x−2021=a−1，代入已知等式化简求出a2的值，进而确定出x−2022的值．
此题考查了完全平方公式，熟练掌握完全平方公式是解本题的关键．
26.解：(1)如图①中，

∵∠ACB=30°，
∴∠ACN=180°−∠ACB=150°，
∵CE平分∠ACN，
∴∠ECN=12∠ACN=75°，
∵PQ//MN，
∠QEC=180°−75°=105°，
∠DEQ=∠QEC−∠CED=60°，
(2)①如图②中，

∵BG//CD，
∴∠GBC=∠DCN，
∵∠DCN=∠ECN−∠ECD=75°−45°=30°，
∠GBC=30°或∠GBC=30°150°，
∴10t=30或10t=360−150，
∴t=3或21．
∴在旋转过程中，若边BG//CD，t的值为3或21．
②如图③中，当EK//BG时，延长EK交MN于R．

由旋转可知：∠GBN=10t°，∠PEK=180°−105°−5t°=(75−5t)°，
∵EK//BG，PQ//MN，
∴∠GBN=∠ERN=∠PEK，
∴10t=75−5t，
解得t=5；
如图④中，当EK//BG时，连接EB．

由旋转可知：∠GBN=10t°，∠PEK=5t°−(180°−105°)=(5t−75)°，则∠GBM=(180−10t)°，
∵EK//BG，PQ//MN，
∴∠PEK+∠PEB+∠EBG=180°，∠GBM+∠EBG+∠PEB=180°，
∴∠GBM=∠PEK，
∴180−10t=5t−75，
解得t=17；
如图⑤，当BG在MN下方时，延长KE交MN于点R，

由旋转可知：∠GBN=(360−10t)°，∠PEK=5t°−(180°−105°)=(5t−75)°，
∵EK//BG，PQ//MN，
∴∠PEK=∠ERM=∠GBN，
∴5t−75=360−10t，
解得t=29；
综上所述，满足条件的t的值为5或17或29．
【解析】(1)如图，先求解∠ACN=180°−∠ACB=150°，∠ECN=12∠ACN=75°，由PQ//MN可得∠QEC=180°−75°=105°，从而可得答案；
(2)①如图，由BG//CD，可得∠GBC=∠DCN，可得∠GBC=30°，再列方程求解即可；②当EK//BG时，分三种情况讨论，分别建立关于t的方程，解方程求出t的值即可．
本题考查的是平行公理的应用，平行线的性质，直角三角形的性质，一元一次方程的应用，理解题意，利用数形结合，清晰的分类讨论都是解本题的关键．个数
17
12
10
7
2
人数
2
3
4
5
1
成绩/分
6
7
8
9
10
人数
2
1
a
b
3