2024年吉林省吉林市第七中学九上数学开学质量跟踪监视试题【含答案】

这是一份2024年吉林省吉林市第七中学九上数学开学质量跟踪监视试题【含答案】，共20页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）欧几里得是古希腊数学家，所著的《几何原本》闻名于世．在《几何原本》中，形如x2+ax＝b2的方程的图解法是：如图，以和b为直角边作Rt△ABC，再在斜边上截取BD＝，则图中哪条线段的长是方程x2+ax＝b2的解？答：是（ ）
A．ACB．ADC．ABD．BC
2、（4分）下列分解因式正确的是（ ）
A．－a＋a3=－a(1＋a2)B．2a－4b＋2=2(a－2b)
C．a2－4=(a－2)2D．a2－2a＋1=(a－1)2
3、（4分）如图，在△ABC中，D、E分别为AC、BC的中点，AF平分∠CAB，交DE于点F，若DF=3，则AC的长为（ ）
A．B．C．D．
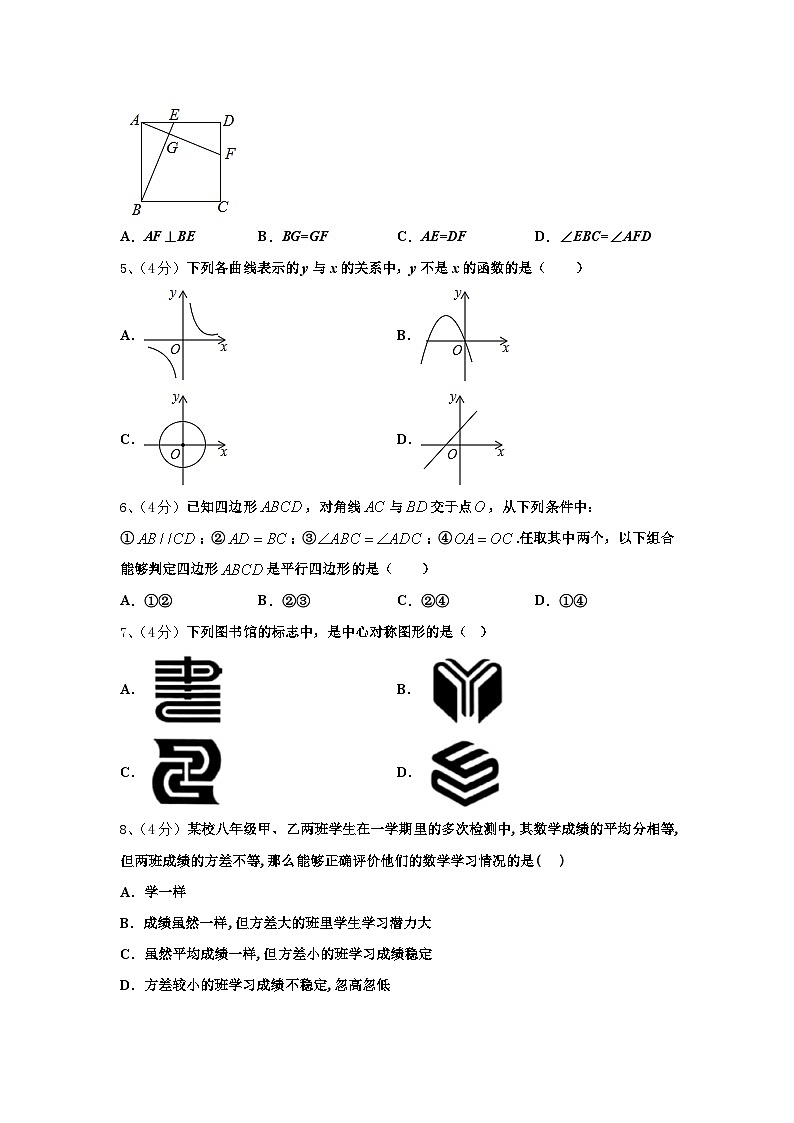
4、（4分）如图，四边形ABCD是正方形，点E、F分别在AD、CD上，AF、BE相交于点G，且AF=BE，则下列结论不正确的是：（ ）
A．AF⊥BEB．BG=GFC．AE=DFD．∠EBC=∠AFD
5、（4分）下列各曲线表示的y与x的关系中，y不是x的函数的是（ ）
A．B．
C．D．
6、（4分）已知四边形，对角线与交于点，从下列条件中：①；②；③；④.任取其中两个，以下组合能够判定四边形是平行四边形的是（ ）
A．①②B．②③C．②④D．①④
7、（4分）下列图书馆的标志中，是中心对称图形的是（ ）
A．B．
C．D．
8、（4分）某校八年级甲、乙两班学生在一学期里的多次检测中,其数学成绩的平均分相等,但两班成绩的方差不等,那么能够正确评价他们的数学学习情况的是( )
A．学一样
B．成绩虽然一样,但方差大的班里学生学习潜力大
C．虽然平均成绩一样,但方差小的班学习成绩稳定
D．方差较小的班学习成绩不稳定,忽高忽低
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）如图．将平面内Rt△ABC绕着直角顶点C逆时针旋转90°得到Rt△EFC．若AC=2，BC=1，则线段BE的长为__________．
10、（4分）平面直角坐标系中，点关于原点的对称点坐标为______．
11、（4分）当x________时，分式有意义.
12、（4分）如图，将一张矩形纸片ABCD沿EF折叠后，点C落在AB边上的点G处，点D落在点H处．若∠1＝62°，则图中∠BEG的度数为_____．
13、（4分）如图，将直线OA向上平移1个单位，得到一个一次函数的图象，那么这个一次函数的关系式是_______．
三、解答题（本大题共5个小题，共48分）
14、（12分）如图，在梯形中中，，是的中点，，，，，点是边上一动点，设的长为.
（1）当的值为多少时，以点为顶点的三角形为直角三角形；
（2）当的值为多少时，以点为顶点的四边形为平行四边形；
（3）点在边上运动的过程中，以为顶点的四边形能否构成菱形？试说明理由.
15、（8分）如图，在直角坐标系中，每个小方格都是边长为的正方形，的顶点均在格点上，点的坐标是．
先将沿轴正方向向上平移个单位长度，再沿轴负方向向左平移个单位长度得到，画出，点坐标是________；
将绕点逆时针旋转，得到，画出，并求出点的坐标是________；
我们发现点、关于某点中心对称，对称中心的坐标是________．
16、（8分）如图，AD=CB,AB=CD，求证：△ACB≌△CAD
17、（10分）如图，在网格平面直角坐标系中，△ABC的顶点均在格点上．
（1）请把△ABC向上平移2个单位长度，再向左平移1个单位长度得到△A'B′C'，画出△A'B′C’并写出点A′，B′的坐标．
（2）求△ABC的面积．
18、（10分）作平行四边形ABCD的高CE，B是AE的中点，如图．
（1）小琴说：如果连接DB，则DB⊥AE，对吗？说明理由．
（2）如果BE：CE＝1： ，BC＝3cm，求AB．
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）若关于的方程的一个根是，则方程的另一个根是________．
20、（4分）如图，在平面直角坐标系中，菱形ABCD的顶点A在x轴负半轴上，顶点B在x轴正半轴上．若抛物线p=ax2-10ax+8（a＞0）经过点C、D，则点B的坐标为________．
21、（4分）一次函数y=kx+b的图象如图所示，若点A(3，m)在图象上，则m的值是__________.
22、（4分）根据如图所示的程序，当输入x＝3时，输出的结果y＝________．
23、（4分）当x=2时，二次根式的值为________．
二、解答题（本大题共3个小题，共30分）
24、（8分）一个多边形的外角和是内角和的，求这个多边形的边数．
25、（10分）如图一次函数y=kx+b的图象经过点A和点B．
（1)写出点A和点B的坐标并求出k、b的值;
(2)求出当x=时的函数值.
26、（12分）如图，在△ABC中，∠C=90°，∠B=30°，AB的垂直平分线交BC于D，垂足为E，BD=4cm．求AC的长．
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、B
【解析】
解一元二次方程，由求根公式求得， 已知AC、BC，由勾股定理求得AB，则AD等于AB和BD之差，比较AD的长度和x的解即可知结论.
【详解】
x2+ax＝b2 ,
即x2+ax-b2=0 ,
∴
∵∠ACB=90°，
∴AB=，
则
故答案为：B.
本题主要考查一元二次方程的根，与勾股定理，解题关键在于能够求出AB的长度.
2、D
【解析】
根据因式分解的定义进行分析.
【详解】
A、-a+a3=-a（1-a2）=-a（1+a）（1-a），故本选项错误；
B、2a-4b+2=2（a-2b+1），故本选项错误；
C、a2-4=（a-2）（a+2），故本选项错误；
D、a2-2a+1=（a-1）2，故本选项正确．
故选D．
考核知识点：因式分解.
3、C
【解析】
首先根据条件D、E分别是AC、BC的中点可得DE∥AB，再求出∠2=∠3，根据角平分线的定义推知∠1=∠3，则∠1=∠2，所以由等角对等边可得到DA=DF=AC．
【详解】
如图，
∵D、E分别为AC、BC的中点，
∴DE∥AB，
∴∠2=∠3，
又∵AF平分∠CAB，
∴∠1=∠3，
∴∠1=∠2，
∴AD=DF=3，
∴AC=2AD=1．
故选C．
本题考查了三角形中位线定理，等腰三角形的判定与性质．三角形中位线的定理是：三角形的中位线平行于第三边且等于第三边的一半．
4、B
【解析】
由四边形ABCD是正方形，可得AD=BA，∠D=∠BAE=90°，利用直角三角形全等的判定（HL）可得Rt△ABE≌Rt△DAF，可得出边角关系，对应选项逐一验证即可．
【详解】
∵四边形ABCD是正方形，
∴ AD=AB，∠D=∠BAE=90°，
又AF=BE，
∴Rt△ABE≌Rt△DAF（HL），
∴∠ABE=∠DAF，∠AEB=∠DFA，AE=DF，因此C选项正确，
又∵∠DAF+∠DFA =90°，
∴∠DAF+∠AEB=90°，
∴∠AGE=90°，即AF⊥BE，因此A选项正确，
∵∠EBC+∠ABE=90°，∠ABE+∠AEB=90°，∠AEB=∠AFD，
∴∠EBC=∠AFD，因此D选项正确，
∵BE=AF，若BG=GF，则AG=GE，可得，∠DAF=45°，则AF应该为正方形的对角线，从图形来看，AF不是对角线，所以与题目矛盾，所以B选项错误，
故选：B．
考查了正方形的性质，全等三角形的判定和性质，余角的定义，垂直的定义，熟记几何图形的概念，判定和性质定理是解题的关键，注意题目要求选不正确的．
5、C
【解析】
根据函数的意义即可求出答案．函数的意义反映在图象上简单的判断方法是：做垂直x轴的直线在左右平移的过程中与函数图象只会有一个交点．
【详解】
根据函数的意义可知：对于自变量x的任何值，y都有唯一的值与之相对应，所以只有选项C不满足条件．
故选C．
本题主要考查了函数的定义．函数的定义：在一个变化过程中，有两个变量x，y，对于x的每一个取值，y都有唯一确定的值与之对应，则y是x的函数，x叫自变量．
6、D
【解析】
以①④作为条件能够判定四边形ABCD是平行四边形，根据平行得出全等三角形，即可求出OB=OD，根据平行四边形的判定推出即可；
【详解】
以①④作为条件，能够判定四边形ABCD是平行四边形．
理由：∵AB//CD，
∴∠OAB=∠OCD，
在△AOB和△COD中，

∴△AOB≌△COD(ASA)，
∴OB=OD，
∴四边形ABCD是平行四边形．
故选：D．
本题考查平行四边形的全等条件，熟练掌握平行四边形的性质的解题关键
7、C
【解析】
根据中心对称图形的概念判断即可．
【详解】
解：A、不是中心对称图形，故此选项错误；
B、不是中心对称图形，故此选项错误；
C、是中心对称图形，故此选项正确；
D、不是中心对称图形，故此选项错误．
故选：C．
此题主要考查了中心对称图形的概念．把一个图形绕某一点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做中心对称图形，这个点叫做对称中心．
8、C
【解析】
分析：由题意知数学成绩的平均分相等，但他们成绩的方差不等，数学的平均成绩一样，说明甲和乙的平均水平基本持平，方差较小的同学，数学成绩比较稳定，选择学生参加考试时，还要选方差较小的学生．
解答：解：∵数学成绩的平均分相等，但他们成绩的方差不等，
数学的平均成绩一样，说明甲和乙的平均水平基本持平，
方差较小的同学，数学成绩比较稳定，
故选C．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、1
【解析】
试题解析：∵Rt△ABC绕着直角顶点C逆时针旋转90°得到Rt△EFC，
∴CE=CA=2，∠ECF=∠ACB=90°，
∴点E、C、B共线，
∴BE=EC+BC=2+1=1．
10、
【解析】
根据两个点关于原点对称时，它们的坐标符号相反可得答案．
【详解】
∵关于原点的对称两个点坐标符号相反，
∴点关于原点的对称点坐标为，
故答案为：．
此题主要考查了关于原点对称的点的坐标，关键是掌握点的坐标的变化规律．
11、
【解析】
根据分母不等于0列式求解即可．
【详解】
由题意得，x−1≠0，
解得x≠1.
故答案为：≠1.
本题考查分式有意义的条件，熟练掌握分式的基本性质是解题关键.
12、56°
【解析】
根据矩形的性质可得AD//BC，继而可得∠FEC=∠1=62°，由折叠的性质可得∠GEF=∠FEC=62°，再根据平角的定义进行求解即可得.
【详解】
∵四边形ABCD是矩形，
∴AD//BC，
∴∠FEC=∠1=62°，
∵将一张矩形纸片ABCD沿 EF折叠后，点C落在AB边上的点 G 处，
∴∠GEF=∠FEC=62°，
∴∠BEG=180°-∠GEF-∠FEC=56°，
故答案为56°.
本题考查了矩形的性质、折叠的性质，熟练掌握矩形的性质、折叠的性质是解题的关键.
13、y=2x+1
【解析】
试题分析：由原直线上的两点坐标得到平移后的点的坐标，再用待定系数法即可求出平移后的解析式．
解：由图象可知，点(0,0)、(2,4)在直线OA上，
∴向上平移1个单位得到的点是(0,1)(2,5)，
那么这两个点在将直线OA向上平移1个单位，得到一个一次函数的图象y=kx+b上，
则b=1，2k+b=5
解得：k=2.
∴y=2x+1.
故答案为：y=2x+1.
点睛：本题主要考查待定系数法求一次函数的解析式.解题的关键在于根据图象确定出平移后的点的坐标.
三、解答题（本大题共5个小题，共48分）
14、（1）当的值为3或8时，以点为顶点的三角形为直角三角形；（2）当的值为1或11时，以点为顶点的四边形为平行四边形；（3）以点为顶点的四边形能构成菱形，理由详见解析.
【解析】
（1）过AD作于，于，当时，分情况讨论，求出即可；
（2）分为两种情况，画出图形，根据平行四边形的性质推出即可；
（3）化成图形，根据菱形的性质和判定求出BP即可．
【详解】
解（1）如图，分别过AD作于，于
∴
而
∴
∴
若以为顶点的三角形为直角三角形，
则或，（在图中不存在）
当时
∴与重合
∴
当时
∴与重合
∴
故当的值为3或8时，以点为顶点的三角形为直角三角形；
（2）若以点为顶点的四边形为平行四边形，那么，有两种情况：
①当在的左边，
∵是的中点，
∴
∴
②当在的右边，
故当的值为1或11时，以点为顶点的四边形为平行四边形；
（3）由（2）知，当时，以点为顶点的四边形能构成菱形
当时，以点为顶点的四边形是平行四边形，
∴，过作于，
∵，，则，
∴.
∴，
∴
故此时是菱形
即以点为顶点的四边形能构成菱形.
此题考查直角三角形的性质，平行四边形的判定，解题关键在于作辅助线和利用勾股定理进行计算.
15、, , .
【解析】
（1）直接利用平移的性质得出对应点位置进而得出答案；
（2）直接利用旋转的性质得出对应点位置进而得出答案；
（3）直接利用关于点对称的性质得出对称中心即可．
【详解】
(1)如图所示：△A1B1C1,即为所求,点C1坐标是：(−2,1)；
故答案为(−2,1)；
(2)如图所示：△A2B1C2,即为所求,点C2坐标是：(−5,0)；
故答案为(−5,0)；
(3)点C. C2关于某点中心对称,对称中心的坐标是：(−3,−1).
故答案为(−3,−1).
本题考查了坐标系中作图，解题的关键是根据图形找出相对应的点即可.
16、见解析
【解析】
利用SSS即可证明.
【详解】
证明：在△ACB与△CAD中
∴△ACB≌△CAD（SSS）
本题考查的是全等三角形的判定，能够根据SSS证明三角形全等是解题的关键.
17、（1）；；（2）7
【解析】
（1）将A、B、C三点分别按要求平移，即可得出新坐标；；，连接三点，即可得出新三角形；
（2）将△ABC和周围的三个三角形整体长方形，长方形面积很容易得出，分别减去周围三个三角形的面积，即可得出，.
【详解】
解：（1）如图
；
（2）


（1）此题主要考查平面坐标系中的平移问题，对应坐标按要求平移即可得出新坐标；
（2）将△ABC和周围的三个三角形整体长方形，长方形面积很容易得出，分别减去周围三个三角形的面积，即可得出.
18、（1）BD⊥AE，理由见解析；（2）（cm）．
【解析】
（1）直接利用平行四边形的性质得出BD∥CE，进而得出答案；
（2）直接利用勾股定理得出BE的长，进而得出答案．
【详解】
解：（1）对，
理由：∵ABCD是平行四边形，
∴CD∥AB且CD＝AB．
又B是AE的中点，
∴CD∥BE且CD＝BE．
∴BD∥CE，
∵CE⊥AE，
∴BD⊥AE；
（2）设BE＝x，则CE＝x，
在Rt△BEC中：x2+（x）2＝9，
解得：x＝，
故AB＝BE＝（cm）．
此题主要考查了平行四边形的性质以及勾股定理，正确应用平行四边形的性质是解题关键．
一、填空题（本大题共5个小题，每小题4分，共20分）
19、-2
【解析】
根据一元二次方程根与系数的关系求解即可.
【详解】
设方程的另一个根为x1，
∵方程的一个根是，
∴x1+0=﹣2，即x1=﹣2.
故答案为：﹣2.
本题主要考查一元二次方程的根与系数的关系（韦达定理），
韦达定理：若一元二次方程ax2+bx+c=0(a≠0)有两个实数根x1，x2，那么x1+x2=﹣，x1x2=.
20、（4，0）
【解析】
根据抛物线p＝ax2−10ax＋8（a＞0）经过点C、D和二次函数图象具有对称性，可以求得该抛物线顶点的横坐标和CD的长，然后根据菱形的性质和勾股定理可以求得AO的长，从而可以求得OB的长，进而写出点B的坐标．
【详解】
解：∵抛物线p＝ax2−10ax＋8＝a（x−5）2−25a＋8，
∴该抛物线的顶点的横坐标是x＝5，当x＝0时，y＝8，
∴点D的坐标为：（0，8），
∴OD＝8，
∵抛物线p＝ax2−10ax＋8（a＞0）经过点C、D，CD∥AB∥x轴，
∴CD＝5×2＝10，
∴AD＝10，
∵∠AOD＝90°，OD＝8，AD＝10，
∴AO＝，
∵AB＝10，
∴OB＝10−AO＝10−6＝4，
∴点B的坐标为（4，0），
故答案为：（4，0）
本题考查二次函数的性质、二次函数图象上点的坐标特征、菱形的性质，解答本题的关键是明确题意，利用二次函数的性质和数形结合的思想解答．
21、2.5
【解析】
先用待定系数法求出直线解析式，再将点A代入求解可得．
【详解】
解：将（-2，0）、（0，1）代入y=kx+b，得：，
解得：
∴y=x+1，
将点A（3，m）代入，得：
即
故答案为：2.5
本题主要考查直线上点的坐标特点，熟练掌握待定系数法求函数解析式是解题的关键．
22、1
【解析】
根据自变量与函数值的对应关系，可得相应的函数值．
【详解】
当x=3时，y=﹣3+5=1．
故答案为：1．
本题考查了函数值，将自变量的值代入相应的函数关系式是解题的关键．
23、3
【解析】
【分析】把x=2代入二次根式进行计算即可得.
【详解】把x=2代入得，
==3，
故答案为：3.
【点睛】本题考查了二次根式的值，准确计算是解题的关键.
二、解答题（本大题共3个小题，共30分）
24、七边形.
【解析】
分析：多边形的内角和定理为(n－2)×180°，多边形的外角和为360°，根据题意列出方程求出n的值．
详解：根据题意可得： 解得：
点睛：本题主要考查的是多边形的内角和公式以及外角和定理，属于基础题型．明白这两个公式是解题的关键．
25、.(1)k=－1,b=1 (1)－1
【解析】
（1）由图可直接写出的坐标，将这两点代入联立求解可得出和的值；
（1）由（1）的关系式，将代入可得出函数值.
【详解】
解：（1）由图可得：A（-1，3），B（1，-3），
将这两点代入一次函数y=kx+b得：，
解得：
∴k=-1，b=1；
（1）将x=代入y=-1x+1得：y=-1．
本题考查待定系数法求一次函数解析式，关键在于看出图示的坐标信息.
26、
【解析】
如图，连接AD，根据垂直平分线的性质可得BD＝AD，进而得到∠DAC的度数和DC的长，再根据勾股定理求出AC的长即可.
【详解】
如图，连接AD，
∵ED是AB的垂直平分线，
∴AD＝BD＝4，
∴∠BAD＝∠B＝30°，
∴∠DAC＝30°，
∵DC＝AD＝2，
∴AC＝.
故答案是.
本题主要考查垂直平分线的性质以及三角函数，求出∠DAC的大小是解题的关键.
题号
一
二
三
四
五
总分
得分
批阅人