2024年福建省泉州第十六中学九上数学开学教学质量检测试题【含答案】

这是一份2024年福建省泉州第十六中学九上数学开学教学质量检测试题【含答案】，共21页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）在平面直角坐标系中，将直线l1：y＝﹣2x﹣2平移后，得到直线l2：y＝﹣2x+4，则下列平移作法正确的是（ ）
A．将l1向右平移3个单位长度B．将l1向右平移6个单位长度
C．将l1向上平移2个单位长度D．将l1向上平移4个单位长度
2、（4分）某灯泡厂为测量一批灯泡的使用寿命，从中抽查了100只灯泡．它们的使用寿命如下表所示：
这批灯泡的平均使用寿命是（ ）
A．1120小时B．1240小时C．1360小时D．1480小时
3、（4分）点P（﹣1，2）关于y轴对称的点的坐标是（ ）
A．（1，2）B．（﹣1，2）C．（1，﹣2）D．（﹣1，﹣2）
4、（4分）一组数:3，5，4，2，3的中位数是( )
A．2B．3C．3.5D．4
5、（4分）如图所示是一些常用图形的标志，其中是轴对称图形但不是中心对称图形的是（ ）
A．A B．B C．C D．D
6、（4分）下列说法正确的是（ ）
A．是二项方程B．是二元二次方程
C．是分式方程D．是无理方程
7、（4分）若一个五边形有三个内角都是直角，另两个内角的度数都等于，则等于( )
A．B．C．D．
8、（4分）已知数据：1，2，0，2，﹣5，则下列结论错误的是（ ）
A．平均数为0B．中位数为1C．众数为2D．方差为34
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）如图：在平面直角坐标系中，直线l：y=x-1与x轴交于点A1，如图所示依次作正方形A1B1C1O、正方形A2B2C2C1、…、正方形AnBnCnCn-1，使得点A1、A2、A3、…在直线l上，点C1、C2、C3、…在y轴正半轴上，则点B2018的坐标是______．
10、（4分）如图，已知在△ABC中，BC边上的高AD与AC边上的高BE交于点F，且∠BAC=45°，BD=6，CD=4，则△ABC的面积为_____．
11、（4分）已知反比例函数，当时，y的取值范围是________．
12、（4分）已知函数，当时，函数值为______．
13、（4分）若等腰三角形的两条边长分别为8cm和16cm，则它的周长为_____cm．
三、解答题（本大题共5个小题，共48分）
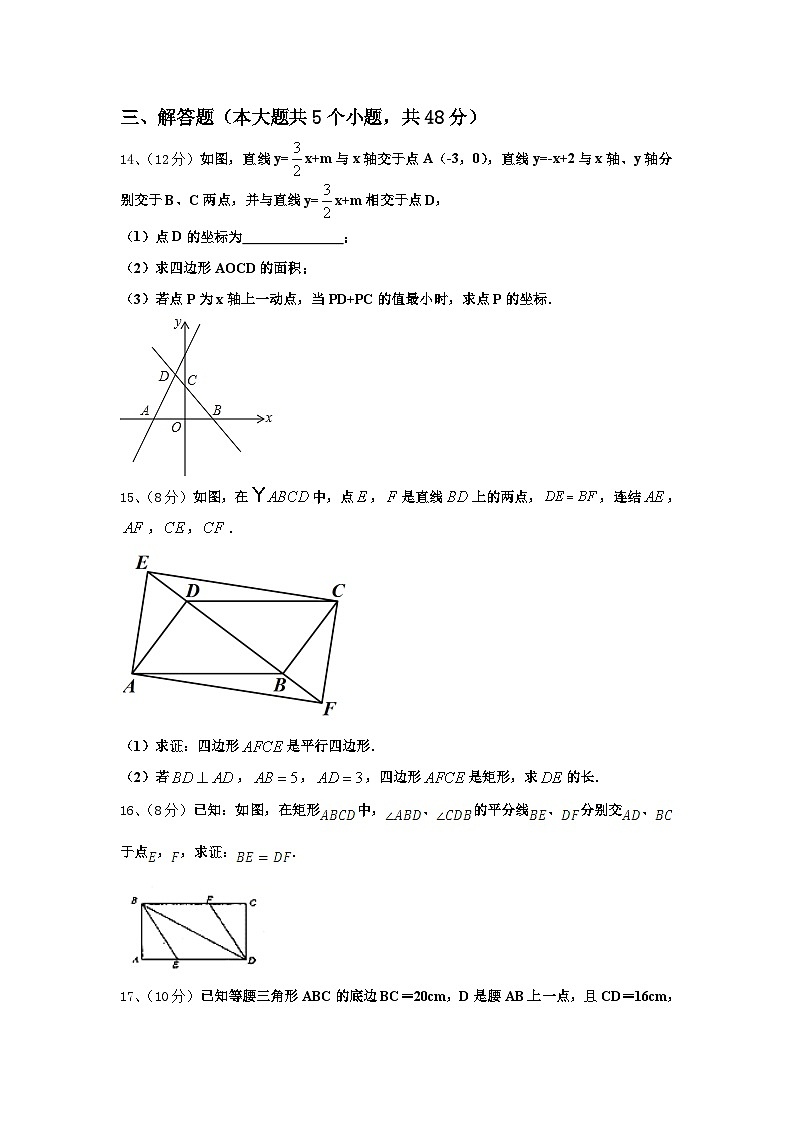
14、（12分）如图，直线y=x+m与x轴交于点A（-3，0），直线y=-x+2与x轴、y轴分别交于B、C两点，并与直线y=x+m相交于点D，
（1）点D的坐标为 ；
（2）求四边形AOCD的面积；
（3）若点P为x轴上一动点，当PD+PC的值最小时，求点P的坐标．
15、（8分）如图，在中，点，是直线上的两点，，连结，，，．
（1）求证：四边形是平行四边形．
（2）若，，，四边形是矩形，求的长．
16、（8分）已知：如图，在矩形中，、的平分线、分别交、于点，，求证：.
17、（10分）已知等腰三角形ABC的底边BC＝20cm，D是腰AB上一点，且CD＝16cm，BD＝12cm．
(1)求证：CD⊥AB；
(2)求该三角形的腰的长度．
18、（10分）如图，在中，，，的垂直平分线分别交和于点、.求证：.
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）△ABC中，AB=15，AC=13，高AD=12，则△ABC的面积为______________．
20、（4分）点A（a,b）是一次函数y=x+2与反比例函数的图像的交点，则__________。
21、（4分）如图矩形ABCD的对角线AC和BD相交于点O，过点O的直线分别交AD和BC于点E，F，AB＝3，BC＝4，则图中阴影部分的面积为_____．
22、（4分）计算：=__．
23、（4分）准备在一块长为30米，宽为24米的长方形花圃内修建四条宽度相等，且与各边垂直的小路，(如图所示)四条小路围成的中间部分恰好是一个正方形，且边长是小路宽度的4倍，若四条小路所占面积为80平方米，则小路的宽度为_____米．
二、解答题（本大题共3个小题，共30分）
24、（8分）如果关于x的方程1+=的解，也是不等式组的解，求m的取值范围．
25、（10分）阅读下列材料：
关于x的方程：的解是，；即的解是；的解是，；的解是，；
请观察上述方程与解的特征，比较关于x的方程与它们的关系，猜想它的解是什么？并利用“方程的解”的概念进行验证．
由上述的观察、比较、猜想、验证，可以得出结论：
如果方程的左边是未知数与其倒数的倍数的和，方程的右边的形式与左边完全相同，只是把其中的未知数换成了某个常数，那么这样的方程可以直接得解，请用这个结论解关于x的方程：．
26、（12分） “扫黑除恶”受到广大人民的关注，某中学对部分学生就“扫黑除恶”知识的了解程度，采用随机抽样调查的方式，并根据收集到的信息进行统计，绘制了下面两幅尚不完整的统计图，请你根据统计图中所提供的信息解答下列问题：
（1）接受问卷调查的学生共有_______人，扇形统计图中“很了解”部分所对应扇形的圆心角为_______；
（2）请补全条形统计图；
（3）若该中学共有学生900人，请根据上述调查结果，估计该中学学生中对“扫黑除恶”知识达到“很了解”和“基本了解”程度的总人数.
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、A
【解析】
利用一次函数图象的平移规律，左加右减，上加下减，得出即可．
【详解】
∵将直线l1：y=-2x-2平移后，得到直线l2：y=-2x+4，
∴-2（x+a）-2=-2x+4，
解得：a=-3，
故将l1向右平移3个单位长度．
故选A．
此题主要考查了一次函数图象与几何变换，正确把握变换规律是解题关键．
2、B
【解析】
先用每组的组中值表示这组的使用寿命，然后根据加权平均数的定义计算．
【详解】
根据题意得：（800×30+1200×30+1600×40）
=×124000
=1240（h）．
则这批灯泡的平均使用寿命是1240h．
故选B．
本题考查了加权平均数：若n个数x1，x2，x3，…，xn的权分别是w1，w2，w3，…，wn，则（x1w1+x2w2+…+xnwn）÷（w1+w2+…+wn）叫做这n个数的加权平均数．
3、A
【解析】
解：根据关于y轴对称，横坐标互为相反数，纵坐标不变．故应选A
考点：关于x轴、y轴对称的点的坐标
4、B
【解析】
按大小顺序排列这组数据，最中间那个数是中位数．
【详解】
解：从小到大排列此数据为：2，1，1，4，5，位置处于最中间的数是1，
所以这组数据的中位数是1．
故选：B．
此题主要考查了中位数．找中位数的时候一定要先排好顺序，然后再根据奇数和偶数个来确定中位数，如果数据有奇数个，则正中间的数字即为所求，如果是偶数个则找中间两位数的平均数．
5、B
【解析】
A、是轴对称图形，是中心对称图形，故本选项错误；
B、是轴对称图形，不是中心对称图形，故本选项正确；
C、不是轴对称图形，也不是中心对称图形，故本选项错误；
D、是中心对称图形，是轴对称图形，故本选项错误．
故选B．
6、A
【解析】
根据整式方程、分式方程和无理方程的概念逐一判断即可得．
【详解】
A．方程是一般式，且方程的左边只有2项，此方程是二项方程，此选项正确；
B．x2y−y＝2是二元三次方程，此选项错误；
C．是一元一次方程，属于整式方程，此选项错误；
D．是一元二次方程，属于整式方程；
故选A．
本题主要考查无理方程，解题的关键是掌握整式方程、分式方程和无理方程的定义．
7、C
【解析】
多边形的内角和可以表示成（n-2）•180°，因为所给五边形有三个角是直角，另两个角都等于α，列方程可求解．
【详解】
依题意有
3×90+2α=（5-2）•180，
解得α=1．
故选C．
本题考查根据多边形的内角和计算公式求多边形的内角，解答时要会根据公式进行正确运算、变形和数据处理．
8、D
【解析】
根据平均数、方差的计算公式和中位数、众数的定义分别进行解答，即可得出答案．
【详解】
A.这组数据：1，2，0，2，﹣5的平均数是：(1+2+0+2-5)÷5=0，故本选项正确；
B.把这组数按从小到大的顺序排列如下：-5，0，1，2，2，可观察1处在中间位置，所以中位数为1，故本选项正确；
C.观察可知这组数中出现最多的数为2，所以众数为2，故本选项正确；
D. ，故本选项错误，
所以选D
本题考查众数，算术平均数，中位数，方差；熟练掌握平均数、方差的计算公式和中位数、众数的定义是解决本题的关键.由于它们的计算由易到难为众数、中位数、算术平方根、方差，所以考试时可按照这样的顺序对选项进行判断，例如本题前三个选项正确，直接可以选D，就可以不用计算方差了.
二、填空题（本大题共5个小题，每小题4分，共20分）
9、
【解析】
【分析】先求出B1、B2、B3的坐标，探究规律后即可解决问题．
【详解】∵y=x-1与x轴交于点A1，
∴A1点坐标（1，0），
∵四边形A1B1C1O是正方形，
∴B1坐标（1，1），
∵C1A2∥x轴，
∴A2坐标（2，1），
∵四边形A2B2C2C1是正方形，
∴B2坐标（2，3），
∵C2A3∥x轴，
∴A3坐标（4，3），
∵四边形A3B3C3C2是正方形，
∴B3（4，7），
∵B1（20，21-1），B2（21，22-1），B3（22，23-1），…，
∴B2018坐标（22018-1，22018-1）．
故答案为
【点睛】本题考查一次函数图象上点的特征，正方形的性质等知识，解题的关键是学会从特殊到一般的探究方法，利用规律解决问题，属于中考填空题中的压轴题．
10、1
【解析】
分析：首先证明△AEF≌△BEC，推出AF=BC=10，设DF=x．由△ADC∽△BDF，推出，构建方程求出x即可解决问题；
详解：∵AD⊥BC，BE⊥AC，
∴∠AEF=∠BEC=∠BDF=90°，
∵∠BAC=45°，
∴AE=EB，
∵∠EAF+∠C=90°，∠CBE+∠C=90°，
∴∠EAF=∠CBE，
∴△AEF≌△BEC，
∴AF=BC=10，设DF=x．
∵△ADC∽△BDF，
∴，
∴，
整理得x2+10x﹣24=0，
解得x=2或﹣12（舍弃），
∴AD=AF+DF=12，
∴S△ABC=•BC•AD=×10×12=1．
故答案为1．
点睛：本题考查勾股定理、等腰三角形的判定和性质等知识，解题的关键是正确寻找全等三角形或相似三角形解决问题，学会利用参数构建方程解决问题，属于中考常考题型．
11、
【解析】
利用反比例函数的性质，由x的取值范围并结合反比例函数的图象解答即可．
【详解】
∵k=1＞0，
∴在每个象限内y随x的增大而减小，
又∵当x=1时，y=1，
当x=2时，y=5，
∴当1＜x＜2时，5＜y＜1．
故答案为．
本题主要考查反比例函数的性质，当k＞0时，在每一个象限内，y随x的增大而减小；当k＜0时，在每一个象限，y随x的增大而增大．
12、5
【解析】
根据x的值确定函数解析式代入求y值.
【详解】
解：因为>0,所以
故答案为5
本题考查了函数表达式，正确选择相应自变量范围内的函数表达式是解题的关键.
13、1；
【解析】
根据已知条件和三角形三边关系可知；等腰三角形的腰长不可能为3cm，只能为8cm，依此即可求得等腰三角形的周长．
【详解】
解：∵等腰三角形的两条边长分别为3cm，8cm，
∴由三角形三边关系可知；等腰三角形的腰长不可能为8cm，只能为16cm，
∴等腰三角形的周长=16+16+8=1cm．
故答案为1．
本题考查了三角形三边关系及等腰三角形的性质，关键是要分两种情况解答．
三、解答题（本大题共5个小题，共48分）
14、（1）（-1，3）；（2）；(3) （-，0）．
【解析】
（1）把A、B的坐标代入函数解析式，求出函数解析式，即可求出D点的坐标；
（2）根据面积公式求出面积即可；
（3）找出P点的位置，求出直线EC的解析式，即可求出PD点的坐标．
【详解】
解：（1）把A（-3，0）代入y=x+m，得m=，
∵直线y=-x+2与x轴、y轴分别交于B、C两点，
∴B点坐标为（2，0），C（0，2），
解方程组得：，
∴D点坐标为（-1，3）；
故答案为（-1，3）；
（2）∵直线y=-x+2与x轴、y轴分别交于B、C两点，
∴B点坐标为（2，0），C（0，2），
∴四边形AOCD的面积=S△DAB-S△COB
=×5×3-×2×2
=；
（3）作D关于x轴的对称点E，连接CE，交x轴于P，此时PD+PC的值最小，
∵D点坐标为（-1，3），
∴E点的坐标为（-1，-3），
设直线CE的解析式为y=ax+b，
把E、C的坐标代入得：
解得：a=5，b=2，
即直线CE的解析式为y=5x+2，
当y=0时，x=-，
即P点的坐标为（-，0）．
本题考查了函数图象上点的坐标特征，轴对称-最短路线问题等知识点，能综合运用知识点进行计算是解此题的关键．
15、 (1)见解析；（2）
【解析】
（1）连结交于点,由四边形ABCD是平行四边形,可得OA=OC,OD=OB,又因为，从而OE=OF,可证四边形是平行四边形；
（2）由勾股定理可求出BD的长，进而求出OD的长，再由勾股定理求出AO的长，根据矩形的性质可知AO=EO，从而可求出DE的长.
【详解】
（1）连结交于点,
∵四边形ABCD是平行四边形,
∴OA=OC,OD=OB,
∵，
∴OE=OF,
四边形是平行四边形;
（2），，，
，
，
.
四边形是矩形，
，，，
，
.
本题考查了平行四边形的判定与性质，矩形的性质，勾股定理等知识，熟练掌握平行四边形的判定与性质是解答（1）的关键，熟练掌握矩形的性质是解（2）的关键.
16、证明过程见解析
【解析】
求证BE=DF，即求证△ABE△CDF.
【详解】
证明：∵、的平分线、分别交、于点，
∴∠ABE=∠EBD，∠BDF=∠FDC
又四边形ABCD为矩形
∴∠ABD=∠CDB，AB=CD
∴∠ABE=∠EBD=∠BDF=∠FDC
在△ABE和△CDF中
∴△ABE△CDF
∴BE=DF
本题主要考查了平行线以及全等三角形的性质，全等三角形的判定是解决本题的关键.
17、（1）见解析；（2）
【解析】
试题分析：根据勾股定理的逆定理直接证明即可.
设腰长为x，则，根据勾股定理列出方程，解方程即可.
试题解析：
（1）∵BC＝20cm，CD＝16cm，BD＝12cm，满足，
根据勾股定理逆定理可知，∠BDC＝90°，即CD⊥AB；
（2）设腰长为x，则，由上问可知，
即：，解得：腰长.
点睛：勾股定理的逆定理：如果三角形中，两条边的平方和等于第三条边的平方，那么这个三角形是直角三角形.
18、详见解析
【解析】
连接BE，由垂直平分线的性质可求得∠EBC=∠ABE=∠A=30°，在Rt△BCE中，由直角三角形的性质可证得BE=2CE，则可证得结论.
【详解】
证明：连接，

为边为垂直平分线，
.
，，
，
，
在中，，
，
.
本题主要考查了含30°角的直角三角形的性质，线段垂直平分线的性质，掌握线段垂直平分线上的点到线段两端点的距离相等是解题的关键．
一、填空题（本大题共5个小题，每小题4分，共20分）
19、84或24
【解析】
分两种情况考虑：
①当△ABC为锐角三角形时，如图1所示，
∵AD⊥BC，
∴∠ADB=∠ADC=90°，
在Rt△ABD中，AB=15，AD=12，
根据勾股定理得：BD==9，
在Rt△ADC中，AC=13，AD=12，
根据勾股定理得：DC==5，
∴BC=BD+DC=9+5=14，
则S△ABC=BC⋅AD=84；
②当△ABC为钝角三角形时，如图2所示，
∵AD⊥BC，
∴∠ADB=90°，
在Rt△ABD中，AB=15，AD=12，
根据勾股定理得：BD==9，
在Rt△ADC中，AC=13，AD=12，
根据勾股定理得：DC==5，
∴BC=BD−DC=9−5=4，
则S△ABC=BC⋅AD=24.
综上，△ABC的面积为24或84.
故答案为24或84.
点睛：此题考查了勾股定理，利用了分类讨论的数学思想，灵活运用勾股定理是解本题的关键.
20、-8
【解析】
把点A（a，b）分别代入一次函数y=x-1与反比例函数 ，求出a-b与ab的值，代入代数式进行计算即可．
【详解】
∵点A(a,b)是一次函数y=x+2与反比例函数的交点，
∴b=a+2,，即a−b=-2，ab=4，
∴原式=ab(a−b)=4×（-2）=-8.
反比例函数与一次函数的交点问题，对于本题我们可以先分别把点代入两个函数中，在对函数和所求的代数式进行适当变形，然后整体代入即可.
21、1．
【解析】
首先结合矩形的性质证明△AOE≌△COF，得△AOE、△COF的面积相等，从而将阴影部分的面积转化为△BCD的面积．
【详解】
∵四边形ABCD是矩形，
∴OA＝OC，∠AEO＝∠CFO；
又∵∠AOE＝∠COF，
在△AOE和△COF中，
∵，
∴△AOE≌△COF（ASA），
∴S△AOE＝S△COF，
∴S阴影＝S△AOE+S△BOF+S△COD＝S△AOE+S△BOF+S△COD＝S△BCD；
∵S△BCD＝BC•CD＝1，
∴S阴影＝1．
故答案为1．
本题主要考查矩形的性质，三角形全等的判定和性质定理，掌握三角形的判定和性质定理，是解题的关键．
22、2
【解析】
解：．故答案为．
23、1.25
【解析】
设小路的宽度为，根据图形所示，用表示出小路的面积，由小路面积为80平方米，求出未知数.
【详解】
设小路的宽度为，由题意和图示可知，小路的面积为
，解一元二次方程，由，可得.
本题综合考查一元二次方程的列法和求解，这类实际应用的题目，关键是要结合题意和图示，列对方程.
二、解答题（本大题共3个小题，共30分）
24、且．
【解析】
先根据分式方程的解法求解方程,再根据分式方程解的情况分类讨论求m的取值,
再解不等式组,根据不等式组的解集和分式方程解的关系即可求解.
【详解】
方程两边同乘,得，,解得,
当时,,,
当时,,,
故当或时有,
方程的解为,其中且,
解不等式组得解集,
由题意得且,解得且,
的取值范围是且.
本题主要考查解含参数的分式方程和解不等式组,解决本题的关键是要熟练掌握解含参数的分式方程.
25、猜想的解是，．验证见解析；，．
【解析】
此题为阅读分析题，解此题要注意认真审题，找到规律：的解为，．据规律解题即可．
【详解】
猜想的解是，．
验证：当时，方程左边，方程右边，
方程成立；
当时，方程左边，方程右边，
方程成立；
的解是，；
由得，
，，
，．
考查解分式方程，通过观察，比较，猜想，验证，可以得出结论.解决此题的关键是理解题意，认真审题，寻找规律.
26、（1）60，108°；（2）见解析；（3）该中学学生中对校园安全知识达到“很了解”和“基本了解”程度的总人数为72人.
【解析】
（1）由很了解的有18人，占30%，可求得接受问卷调查的学生数，继而求得扇形统计图中“很了解”部分所对应扇形的圆心角；（2）由（1）可求得基本了解很少的人数，继而补全条形统计图；（3）利用样本估计总体的方法，即可求得答案.
【详解】
（1）接受问卷调查的学生共有：18÷30%＝60（人）；
∴扇形统计图中“很了解”部分所对应扇形的圆心角为：360°×30%＝108°；
故答案为：60，108°；
（2）60﹣3﹣9﹣18＝30；
补全条形统计图得：
（3）根据题意得：900×＝720（人），
则估计该中学学生中对校园安全知识达到“很了解”和“基本了解”程度的总人数为72人.
本题考查的是条形统计图的综合运用.读懂统计图，从统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据.
题号
一
二
三
四
五
总分
得分
批阅人
使用寿命x/小时
600≤x≤1000
1000≤x≤1400
1400≤x≤1800
灯泡数/个
30
30
40