2024-2025学年四川省遂宁市泸州市石洞镇中学心学校数学九年级第一学期开学质量检测试题【含答案】

这是一份2024-2025学年四川省遂宁市泸州市石洞镇中学心学校数学九年级第一学期开学质量检测试题【含答案】，共22页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）若直角三角形的两条直角边的长分别为6和8，则斜边上的中线长是（ ）
A．6B．5C．7D．不能确定
2、（4分）计算结果正确的是（ ）
A．B．C．D．
3、（4分）若一次函数y=kx+17的图象经过点（-3，2），则k的值为（ ）
A．-6 B．6 C．-5 D．5
4、（4分）若3x ＞﹣3y，则下列不等式中一定成立的是（ ）
A．x＞yB．x＜yC．x﹣y＞0D．x+y＞0
5、（4分）计算（ ）
A．7B．-5C．5D．-7
6、（4分）已知a为整数，且＜＜，则a等于（）
A．1B．2C．3D．4
7、（4分）某校八年级学生去距学校10km的科技馆参观，一部分学生骑自行车，过了30min，其余学生乘汽车出发，结果他们同时到达．已知汽车的速度是骑自行车学生速度的4倍，设骑自行车学生的速度为xkm/h，则下列方程正确的是（ ）
A．B．C．D．
8、（4分）电话每台月租费元，市区内电话(三分钟以内)每次元，若某台电话每次通话均不超过分钟，则每月应缴费(元)与市内电话通话次数之间的函数关系式是( )
A．B．
C．D．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）如果最简二次根式和是同类二次根式，那么a=_______
10、（4分）一次函数的图象与轴的交点坐标是________．
11、（4分）一次函数的图象不经过第_______象限.
12、（4分）如图，在平面直角坐标系中，过点分别作轴于点，轴于点，、分别交反比例函数的图像于点、，则四边形的面积为__________．
13、（4分）如图，已知矩形的对角线相交于点，过点任作一条直线分别交，于，，若，，则阴影部分的面积是______.
三、解答题（本大题共5个小题，共48分）
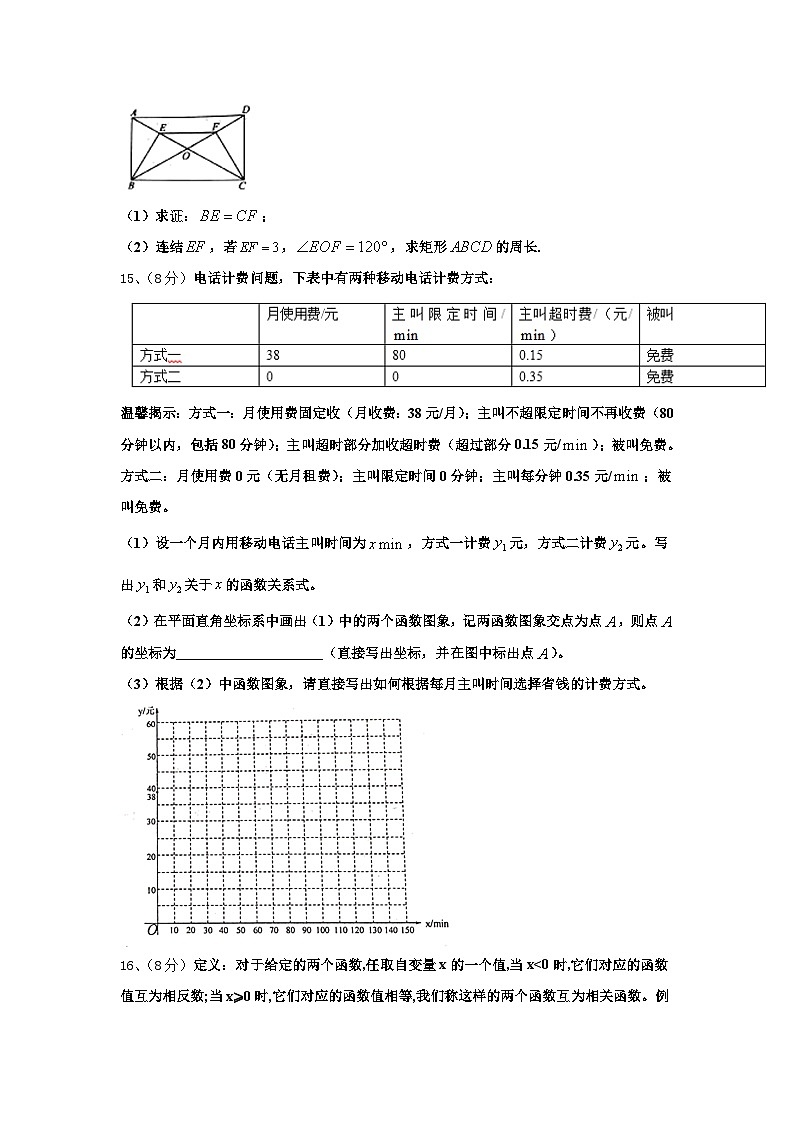
14、（12分）如图，在矩形中，对角线与相交于点，点，分别是，的中点，连结，.
（1）求证：；
（2）连结，若，，求矩形的周长.
15、（8分）电话计费问题，下表中有两种移动电话计费方式：
温馨揭示：方式一：月使用费固定收（月收费：38元/月）；主叫不超限定时间不再收费（80分钟以内，包括80分钟）；主叫超时部分加收超时费（超过部分0.15元/）；被叫免费。
方式二：月使用费0元（无月租费）；主叫限定时间0分钟；主叫每分钟0.35元/；被叫免费。
（1）设一个月内用移动电话主叫时间为，方式一计费元，方式二计费元。写出和关于的函数关系式。
（2）在平面直角坐标系中画出（1）中的两个函数图象，记两函数图象交点为点，则点的坐标为_____________________（直接写出坐标，并在图中标出点）。
（3）根据（2）中函数图象，请直接写出如何根据每月主叫时间选择省钱的计费方式。
16、（8分）定义：对于给定的两个函数,任取自变量x的一个值,当x<0时,它们对应的函数值互为相反数;当x⩾0时,它们对应的函数值相等,我们称这样的两个函数互为相关函数。例如：一次函数y=x−1,它们的相关函数为y= .
(1)已知点A(−5,8)在一次函数y=ax−3的相关函数的图象上，求a的值；
(2)已知二次函数y=−x+4x− .
①当点B(m, )在这个函数的相关函数的图象上时，求m的值；
②当−3⩽x⩽3时,求函数y=−x+4x−的相关函数的最大值和最小值.
17、（10分）在平行四边形ABCD中，连接BD，过点B作BE⊥BD于点B交DA的延长线于点E，过点B作BG⊥CD于点G．
（1）如图1，若∠C＝60°，∠BDC＝75°，BD＝6，求AE的长度；
（2）如图2，点F为AB边上一点，连接EF，过点F作FH⊥FE于点F交GB的延长线于点H，在△ABE的异侧，以BE为斜边作Rt△BEQ，其中∠Q＝90°，若∠QEB＝∠BDC，EF＝FH，求证：BF+BH＝BQ．
18、（10分）如图所示,在边长为1的网格中作出△ABC绕点A按逆时针方向旋转90∘,再向下平移2格后的图形△A′B′C′.
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）如图①，在▱ABCD中，∠B＝120°，动点P从点B出发，沿BC、CD、DA运动至点A停止，设点P运动的路程为xcm，△PAB的面积为ycm2，y关于x的函数的图象如图②所示，则图②中H点的横坐标为_____．
20、（4分）在设计人体雕像时，使雕像的上部（腰以上）与下部（腰以下）的高度比，等于下部与全部（全身）的高度比，可以增加视觉美感.按此比例，如果雕像的高度为 1m，那么它的下部应设计的高度为_____．
21、（4分）如果多项式是一个完全平方式，那么k的值为______．
22、（4分）式子在实数范围内有意义，则x的取值范围是_____．
23、（4分）如图，在菱形中，，菱形的面积为24，则菱形周长为________
二、解答题（本大题共3个小题，共30分）
24、（8分）李刚家去年养殖的“丰收一号”多宝鱼喜获丰收，上市20天全部售完，李刚对销售情况进行了跟踪记录，并将记录情况绘成图象，日销售量y(单位：千克)与上市时间x(单位：天)的函数关系如图所示.
（1）观察图象，直接写出日销售量的最大值；
（2）求李刚家多宝鱼的日销售量y与上市时间x的函数解析式.
25、（10分）近年来雾霾天气给人们的生活带来很大影响，空气质量问题倍受人们关注，某单位计划在室内安装空气净化装置，需购进A，B两种设备，每台B种设备价格比每台A种设备价格多700元，花3000元购买A种设备和花7200元购买B种设备的数量相同．
（1）求A种、B种设备每台各多少元？
（2）根据单位实际情况，需购进A，B两种设备共20台，总费用不高于17000元，求A种设备至少要购买多少台？
26、（12分）在平面直角坐标系中，已知点在抛物线（）上，且，
（1）若，求，的值；
（2）若该抛物线与轴交于点，其对称轴与轴交于点，试求出，的数量关系；
（3）将该抛物线平移，平移后的抛物线仍经过，点的对应点，当时，求平移后抛物线的顶点所能达到的最高点的坐标．
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、B
【解析】
首先根据勾股定理，求出斜边长，然后根据直角三角形斜边中线定理，即可得解.
【详解】
根据勾股定理，得斜边长为
则斜边中线长为5，
故答案为B.
此题主要考查勾股定理和斜边中线定理，熟练掌握，即可解题.
2、A
【解析】
直接根据进行计算即可．
【详解】
解：；
故选：A.
本题考查了二次根式的计算与化简，解题的关键是熟练掌握二次根式的运算法则.
3、D
【解析】
由一次函数经过（-3，2），故将x=-3，y=2代入一次函数解析式中，得到关于k的方程，求出方程的解即可得到k的值．
【详解】
由一次函数y=kx+17的图象经过点（-3，2），
故将x=-3，y=2代入一次函数解析式得：2=-3k+17，
解得：k=1，
则k的值为1．
故选D．
此题考查了待定系数法求一次函数解析式，灵活运用待定系数法是解本题的关键．
4、D
【解析】
利用不等式的性质由已知条件可得到x+y＞1，从而得到正确选项．
【详解】
∵3x＞﹣3y，
∴3x+3y＞1，
∴x+y＞1．
故选：D．
本题考查了不等式的性质：应用不等式的性质应注意的问题，在不等式的两边都乘以（或除以）同一个负数时，一定要改变不等号的方向；当不等式的两边要乘以（或除以）含有字母的数时，一定要对字母是否大于1进行分类讨论．
5、C
【解析】
利用最简二次根式的运算即可得.
【详解】

故答案为 C
本题考查二次根式的运算，掌握同类二次根式的运算法则及分母有理化是解题的关键.
6、D
【解析】
根据实数的估算即可求解.
【详解】
∵＜＜，=4
∴a=4
故选D.
此题主要考查实数的估算，解题的关键是熟知实数的性质.
7、A
【解析】
汽车的速度是4xkm/h, 骑自行车所需要的时间=乘汽车的时间+30min,故选A.
8、C
【解析】
本题考查了一次函数的解析式，设为，把k和b代入即可.
【详解】
设函数解析式为：，
由题意得，k=0.2，b=28，
∴函数关系式为：.
故选：C.
本题考查了一次函数解析式的表示，熟练掌握一次函数解析式的表示方法是解题的关键.
二、填空题（本大题共5个小题，每小题4分，共20分）
9、3
【解析】
分析：根据同类二次根式的被开方式相同列方程求解即可.
详解：由题意得，
3a+4=25-4a，
解之得，
a=3.
故答案为：3.
点睛：本题考查了同类二次根式的应用，根据同类二次根式的定义列出关于a的方程是解答本题的关键.
10、 (0，-3)．
【解析】
令x= 0，求出y的值即可得出结论．
【详解】
解:当x=0时，y=-3
∴一次函数的图象与y轴的交点坐标是(0,-3)．
故答案为：(0，-3)．
本题考查的是一次函数图形上点的特征，熟知一次函数图象与坐标轴交点的算法是解答此题的关键．
11、三
【解析】
根据一次函数的性质，k<0，过二、四象限，b>0，与y轴交于正半轴，综合来看即可得到结论.
【详解】
因为解析式中，-5<0,3>0,图象过一、二、四象限，故图象不经过第三象限.
故答案为：第三象限.
12、1
【解析】
根据反比例函数系数k的几何意义可得S△DBO＝S△AOC＝|k|＝1，再利用矩形OCPD的面积减去△BDO和△CAO的面积即可．
【详解】
解：∵B、A两点在反比例函数的图象上，
∴S△DBO＝S△AOC＝×2＝1，
∵P（2，3），
∴四边形DPCO的面积为2×3＝6，
∴四边形BOAP的面积为6﹣1﹣1＝1，
故答案为：1．
此题主要考查了反比例函数k的几何意义，关键是掌握在反比例函数的图象上任意一点象坐标轴作垂线，这一点和垂足以及坐标原点所构成的三角形的面积是|k|，且保持不变．
13、1
【解析】
首先结合矩形的性质证明△AOE≌△COF，得△AOE、△COF的面积相等，从而将阴影部分的面积转化为△AOD的面积．
【详解】
∵四边形ABCD是矩形，∴OA=OC，AD∥BC，∴∠AEO=∠CFO．
在△AOE和△COF中，∵，∴△AOE≌△COF，∴S△AOE=S△COF，∴S阴影= S△COF +S△EOD =S△AOE+S△EOD =S△AOD．
∵S△AODBC•AD=1，∴S阴影=1．
故答案为：1．
本题考查了矩形的性质以及全等三角形的判定和性质，能够根据三角形全等，从而将阴影部分的面积转化为矩形面积的，是解决问题的关键．
三、解答题（本大题共5个小题，共48分）
14、（1）见解析；（2）.
【解析】
（1）欲证明BE＝CF，只要证明△BOE≌△COF即可；
（2）利用三角形中位线定理求出AD，解直角三角形求出AB即可解决问题；
【详解】
解：（1）∵四边形为矩形，
∴，.
∵，分别为，的中点，
∴.
∵，
∴，
∴.
（2）∵，分别为，的中点，
∴为的中位线.
∵，
∴.
∵，
∴，
∴.
∴ .
本题考查矩形的性质，三角形全等的判定和性质以及三角形的中位线定理等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．
15、（1）当时，，当时，，；（2）点的坐标为，见解析；（3）当每月主叫时间小于130分钟时选择方式二省钱；当每月主叫时间等于130分钟时两种方式都一样；当每月主叫时间大于130分钟时选择方式一省钱.
【解析】
（1）根据题意即可写出两种资费的关系式；
（2）根据列表、描点、连线即可画出函数图像，再求出交点坐标A；
（3）根据函数图像的性质即可求解.
【详解】
解：（1）方式一：当时，，
当时，；
方式二：；
或解：（1）方式一：
化简，得；
方式二：；
（2）
点的坐标为
（3）由图象可得，
当每月主叫时间小于130分钟时选择方式二省钱；
当每月主叫时间等于130分钟时两种方式都一样；
当每月主叫时间大于130分钟时选择方式一省钱。
此题主要考查一次函数的应用，解题的关键是根据题意写出函数关系式.
16、（1）1；（2）①m=2− 或m=2+或m=2− ；②最大值为 ,最小值为−.
【解析】
（1）写出y=ax-3的相关函数，代入计算；
（2）①写出二次函数y=−x+4x−的相关函数，代入计算；
②根据二次根式的最大值和最小值的求法解答．
【详解】
(1)y=ax−3的相关函数y= ，
将A(−5,8)代入y=−ax+3得：5a+3=8，
解得a=1；
(2)二次函数y=−x+4x−的相关函数为y= ，
①当m<0时,将B(m, )代入y=x-4x+
得m-4m+，
解得：m=2+ (舍去),或m=2−，
当m⩾0时,将B(m, )代入y=−x+4x−得：
−m +4m− ，
解得：m=2+或m=2−.
综上所述：m=2− 或m=2+或m=2− ；
②当−3⩽x<0时, y=−x+4x−，抛物线的对称轴为x=2，
此时y随x的增大而减小，
∴此时y的最大值为，
当0⩽x⩽3时,函数y=−x+4x−，抛物线的对称轴为x=2，
当x=0有最小值,最小值为−,当x=2时,有最大值,最大值y= ，
综上所述,当−3⩽x⩽3时,函数y=−x+4x−的相关函数的最大值为 ,最小值为−.
此题考查二次函数图象上点的坐标特征，一次函数图象上点的坐标特征，解题关键在于将已知点代入解析式.
17、（1）6﹣2；（2）详见解析．
【解析】
（1）根据平行四边形性质可证：△BDE是等腰直角三角形，运用勾股定理可求DE和AD，AE即可求得；
（2）过点E作ET⊥AB交BA的延长线于T，构造直角三角形，由平行四边形性质及直角三角形性质可证：△BEQ≌△BET（AAS），△BFH≌△TEF（AAS），进而可证得结论．
【详解】
解：（1）如图1，过点D作DR⊥BC于R，
∵ABCD是平行四边形
∴AB∥CD，AD∥BC，AD＝BC
∵∠C＝60°，∠BDC＝75°，
∴∠CBD＝180°﹣（∠C+∠BDC）＝45°
∴∠ADB＝∠CBD＝45°
∵BE⊥BD
∴∠DBE＝90°
∴∠E＝∠BDE＝45°
∴DE＝BD＝12
∵DR⊥BC
∴∠BRD＝∠CRD＝90°
∴∠BDR＝∠CBD＝45°，
∴DR＝BR
由勾股定理可得即
∴DR＝BR＝6
∵∠C＝60°
∴∠CDR＝90°﹣60°＝30°
∴CR＝2，CD＝4
∴AD＝BC＝DR+CR＝6+2，
∴AE＝DE﹣AD＝12﹣（6+2）＝6﹣2；
（2）如图2，过点E作ET⊥AB交BA的延长线于T，则∠T＝90°
∵ABCD是平行四边形
∴AB∥CD，
∴∠ABD＝∠BDC
∵∠QEB＝∠BDC
∴∠QEB＝∠ABD
∵BG⊥CD，BE⊥BD，FH⊥FE
∴∠BGC＝∠ABG＝∠DBE＝∠EFH＝∠Q＝90°
∴∠EBT+∠BET＝∠EBT+∠ABD＝∠EFT+∠BFH＝∠EFT+∠FET＝90°，
∴∠BET＝∠ABD＝∠QEB，∠BFH＝∠FET
∵BE＝BE，EF＝FH
∴△BEQ≌△BET（AAS），△BFH≌△TEF（AAS）
∴BQ＝BT，BH＝FT
∵BF+FT＝BT
∴BF+BH＝BQ．
本题考查了平行四边形的性质、勾股定理以及全等三角形的性质与判定，解题的关键是灵活运用平行四边形及直角三角形的性质．
18、见解析.
【解析】
先作出绕点逆时针旋转的三角形，然后再下平移2格的对应点、、，然后顺次连接即可.
【详解】
如图所示，虚线三角形为绕点按逆时针方向旋转的三角形，
即为所要求作的三角形.
本题考查了利用平移变换与旋转变换作图，本题先作出绕点逆时针旋转的三角形是解题的关键.
一、填空题（本大题共5个小题，每小题4分，共20分）
19、14
【解析】
根据图象点P到达C时，△PAB的面积为6，由BC＝4，∠B＝120°可求得AB＝6，H横坐标表示点P从B开始运动到A的总路程，则问题可解．
【详解】
由图象可知，当x＝4时，点P到达C点，此时△PAB的面积为6
∵∠B＝120°，BC＝4
∴
解得AB＝6
H点表示点P到达A时运动的路程为4+6+4＝14
故答案为14
本题为动点问题的函数图象探究题，考查了一次函数图象性质，解答时注意研究动点到达临界点前后函数图象的变化．
20、
【解析】
设雕像的下部高为x m，则上部长为（1-x）m，然后根据题意列出方程求解即可．
【详解】
解：设雕像的下部高为x m，则题意得：，
整理得：，
解得： 或 (舍去)；
∴它的下部应设计的高度为.
故答案为：.
本题考查了黄金分割，解题的关键在于读懂题目信息并列出比例式，难度不大．
21、8或-4
【解析】
根据完全平方公式的定义即可求解.
【详解】
=为完全平方公式，故=±6，
即得k=8或-4.
此题主要考查完全平方公式的形式，解题的关键是熟知完全平方公式.
22、x≤1
【解析】
二次根式的被开方数是非负数．
【详解】
解：依题意，得
1﹣x≥0，
解得，x≤1．
故答案是：x≤1．
考查了二次根式的意义和性质．概念：式子叫二次根式．性质：二次根式中的被开方数必须是非负数，否则二次根式无意义．
23、20
【解析】
根据菱形面积公式可求BD的长，根据勾股定理可求菱形边长，即可求周长．
【详解】
解：∵S菱形ABCD=AC×BD，
∴24=×8×BD，
∴BD=6，
∵ABCD是菱形，
∴AO=CO=4，BO=DO=3，AC⊥BD，
∴，
∴菱形ABCD的周长为4×5=20.
本题考查了菱形的性质，利用菱形的面积公式求BD的长是本题的关键．
二、解答题（本大题共3个小题，共30分）
24、（1）日销售量的最大值为120千克；（2）李刚家多宝鱼的日销售量y与上市时间x的函数解析式为.
【解析】
分析：（1）观察函数图象，找出拐点坐标即可得出结论；
（2）设李刚家多宝鱼的日销售量y与上市时间x的函数解析式为y=kx+b，分0≤x≤12和12＜x≤20，找出图象上点的坐标，利用待定系数法即可求出函数解析式．
详解：（1）观察图象，发现当x=12时，y=120为最大值，∴日销售量的最大值为120千克．
（2）设李刚家多宝鱼的日销售量y与上市时间x的函数解析式为y=kx+b，
当0≤x≤12时，有，解得：，∴此时日销售量y与上市时间x的函数解析式为y=10x；
当12＜x≤20时，有，解得：，∴此时日销售量y与上市时间x的函数解析式为y=﹣15x+1．
综上可知：李刚家多宝鱼的日销售量y与上市时间x的函数解析式为y=．
点睛：本题考查了一次函数的应用、一次函数的图象以及待定系数法求函数解析式，解题的关键是：（1）观察函数图象，找出最高点；（2）分段利用待定系数法求出函数解析式．本题属于中档题，难度不大，解决该题型题目时，根据函数图象找出点的坐标，利用待定系数法求出函数解析式是关键．
25、（1）每台A种设备500元，每台B种设备1元；（2）A种设备至少要购买2台．
【解析】
（1）设每台A种设备x元，则每台B种设备（x＋700）元，根据数量＝总价÷单价结合花3000元购买A种设备和花7200元购买B种设备的数量相同，即可得出关于x的分式方程，解之并检验后即可得出结论；
（2）设购买A种设备m台，则购买B种设备（20−m）台，根据总价＝单价×数量结合总费用不高于17000元，即可得出关于m的一元一次不等式，解之即可得出m的取值范围，取其内的最小正整数即可．
【详解】
（1）设每台A种设备x元，则每台B种设备（x+700）元，
根据题意得：，
解得：x＝500，
经检验，x＝500是原方程的解，
∴x+700＝1．
答：每台A种设备500元，每台B种设备1元；
（2）设购买A种设备m台，则购买B种设备（20﹣m）台，
根据题意得：500m+1（20﹣m）≤17000，
解得：m≥2．
答：A种设备至少要购买2台．
本题考查了分式方程的应用以及一元一次不等式的应用，正确的理解题意是解题的关键．
26、（1）b=1，c=3；（2）；（3）（，）
【解析】
（1）把代入得，与构成方程组，解方程组即可求得；
（2）求得，，，即可得到，，即可求得；
（3）把化成顶点式，得到，根据平移的规律得到，把代入，进一步得到，即，分类求得，由，得到，即，从而得到平移后的解析式为，得到顶点为，，设，即，即可得到取最大值为，从而得到最高点的坐标．
【详解】
解：（1）把代入，可得，
解，可得，；
（2）由，得．
对于，
当时，．
抛物线的对称轴为直线．
所以，，．
因为，
所以，，
；
（3）由平移前的抛物线，可得
，即．
因为平移后的对应点为
可知，抛物线向左平移个单位长度，向上平移个单位长度．
则平移后的抛物线解析式为，
即．
把代入，得．
．
，
所以．
当时，（不合题意，舍去）；
当时，，
因为，所以．
所以，
所以平移后的抛物线解析式为．
即顶点为，，
设，即．
因为，所以当时，随的增大而增大．
因为，
所以当时，取最大值为，
此时，平移后抛物线的顶点所能达到的最高点坐标为，．
本题是二次函数的综合题，考查了二次函数的图象和系数的关系，二次函数的点的坐标特征，二次函数的图象与几何变换，也考查二次函数的性质．
题号
一
二
三
四
五
总分
得分
批阅人