2024-2025学年江西省上饶市第六中学数学九上开学教学质量检测模拟试题【含答案】

这是一份2024-2025学年江西省上饶市第六中学数学九上开学教学质量检测模拟试题【含答案】，共23页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）晨光中学规定学生的学期体育成绩满分为100分，其中早锻炼及体育课外活动占20%，期中考试成绩占30%,期末考试成绩占50%，小桐三项体育成绩（百分制）依次95分、90分、86分，则小桐这学期的体育成绩是( )
A．88B．89分C．90分D．91分
2、（4分）在Rt△ABC中，∠C＝90°，D为BC上一点，要使点D到AB的距离等于DC，则必须满足（ ）
A．点D是BC的中点
B．点D在∠BAC的平分线上
C．AD是△ABC的一条中线
D．点D在线段BC的垂直平分线上
3、（4分）如图，平行四边形ABCD中，E，F是对角线BD上的两点，如果添加一个条件使△ABE≌△CDF，则添加的条件不能是（ ）
A．AE=CFB．BE=FDC．BF=DED．∠1=∠2
4、（4分）下列说法：
四边相等的四边形一定是菱形
顺次连接矩形各边中点形成的四边形一定是正方形
对角线相等的四边形一定是矩形
经过平行四边形对角线交点的直线，一定能把平行四边形分成面积相等的两部分
其中正确的有 个．
A．4B．3C．2D．1
5、（4分）甲、乙、丙三位选手各10次射击成绩的平均数和方差统计如表：
已知乙是成绩最稳定的选手，且乙的10次射击成绩不都一样，则a的值可能是（ ）
A．0B．0.020C．0.030D．0.035
6、（4分）某商务酒店客房有间供客户居住．当每间房 每天定价为元时，酒店会住满；当每间房每天的定价每增加元时，就会空闲一间房．如果有客户居住，宾馆需对居住的每间房每天支出元的费用．当房价定为多少元时，酒店当天的利润为元?设房价定为元，根据题意，所列方程是( )
A．B．
C．D．
7、（4分）如图，在中，于点，，则的度数是（ ）
A．B．C．D．
8、（4分）某商场要招聘电脑收银员，应聘者需通过计算机、语言和商品知识三项测试，小明的三项成绩（百分制）依次是70分，50分，80分，其中计算算机成绩占50%，语言成绩占30%，商品知识成绩占20%．则小明的最终成绩是（ ）
A．66分B．68分C．70分D．80分
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）因式分解：a2﹣4＝_____．
10、（4分）因式分解：3x3﹣12x=_____．
11、（4分）若恒成立，则A+B＝____．
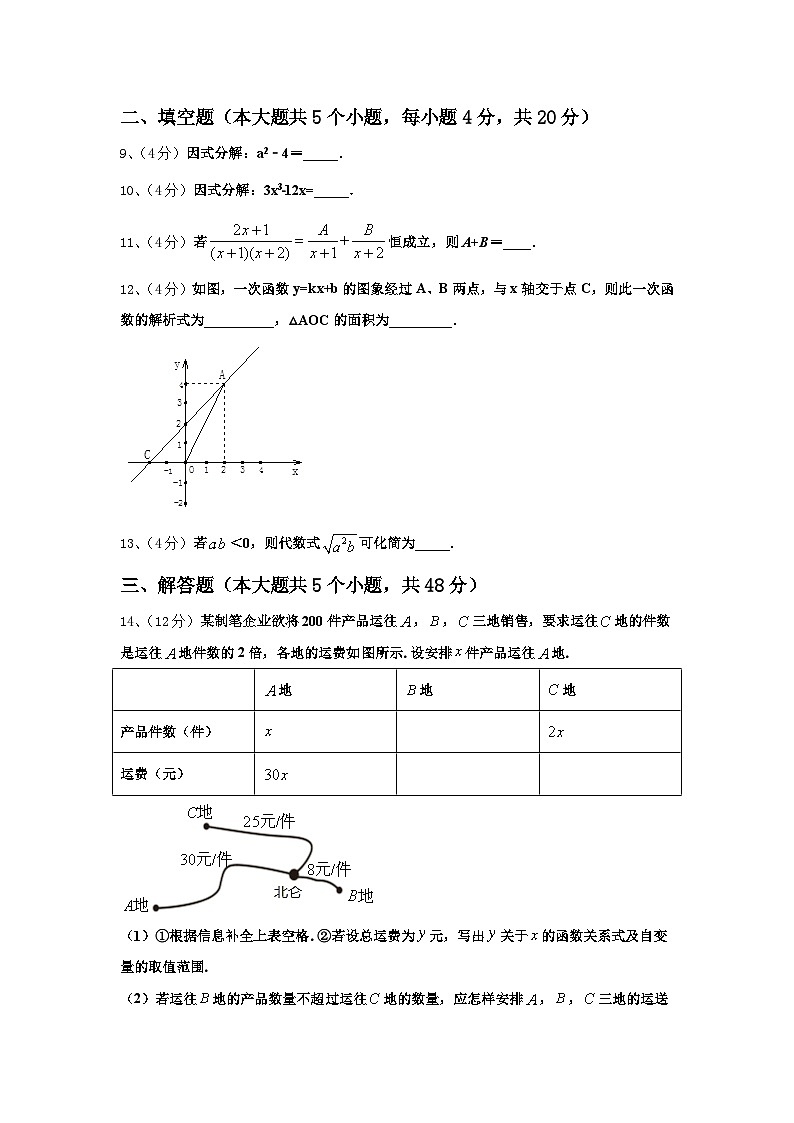
12、（4分）如图，一次函数y=kx+b的图象经过A、B两点，与x轴交于点C，则此一次函数的解析式为__________，△AOC的面积为_________．
13、（4分）若＜0，则代数式可化简为_____.
三、解答题（本大题共5个小题，共48分）
14、（12分）某制笔企业欲将200件产品运往，，三地销售，要求运往地的件数是运往地件数的2倍，各地的运费如图所示.设安排件产品运往地.
（1）①根据信息补全上表空格.②若设总运费为元，写出关于的函数关系式及自变量的取值范围.
（2）若运往地的产品数量不超过运往地的数量，应怎样安排，，三地的运送数量才能达到运费最少.
15、（8分）（1） [探索发现]正方形中,是对角线上的一个动点(与点不重合),过点作交线段于点．求证:
小玲想到的思路是:过点作于点于点,通过证明得到．请按小玲的思路写出证明过程
（2）[应用拓展]如图2,在的条件下，设正方形的边长为,过点作交于点．求的长．
16、（8分）如图,菱形对角线交于点，，，与交于点.
（1）试判断四边形的形状，并说明你的理由；
（2）若,求的长.
17、（10分）如图，方格纸中每个小正方形的边长均为1，我们把每个小正方形的顶点叫做格点． 如：线段AB的两个端点都在格点上．
（1）在图1中画一个以AB为边的平行四边形ABCD，点C、D在格点上，且平行四边形ABCD的面积为15；
（2）在图2中画一个以AB为边的菱形ABEF（不是正方形），点E、F在格点上，则菱形ABEF的对角线AE＝________，BF＝________；
（3）在图3中画一个以AB为边的矩形ABMN（不是正方形），点M、N在格点上，则矩形ABMN的长宽比＝______．

18、（10分）如图，已知△ABC中，三个顶点的坐标是：A（-3，6）、B（-5，3）、C（-2，1）．
（1）画出△ABC向右平移五个单位得到的，并写出的坐标；
（2）画出△ABC关于轴对称的，并写出的坐标．
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）某中学随机抽查了50名学生，了解他们一周的课外阅读时间，结果如下表所示：
则这50名学生一周的平均课外阅读时间是____小时．
20、（4分）直线y＝x﹣与y轴的交点是_____．
21、（4分）从沿北偏东的方向行驶到，再从沿南偏西方向行驶到，则______.
22、（4分）直角三角形的两条直角边长为6，8，那么斜边上的中线长是____．
23、（4分）某市对400名年满15岁的男生的身高进行了测量，结果身高（单位：m）在1.68～1.70这一小组的频率为0.25，则该组的人数为_____．
二、解答题（本大题共3个小题，共30分）
24、（8分）感知：如图（1），已知正方形ABCD和等腰直角△EBF，点E在正方形BC边上，点F在AB边的延长线上，∠EBF=90°，连结AE、CF．
易证：∠AEB=∠CFB（不需要证明）．
探究：如图（2），已知正方形ABCD和等腰直角△EBF，点E在正方形ABCD内部，点F在正方形ABCD外部，∠EBF=90°，连结AE、CF．
求证：∠AEB=∠CFB
应用：如图（3），在（2）的条件下，当A、E、F三点共线时，连结CE，若AE=1，EF=2，则CE=______．
25、（10分）我市某游乐场在暑假期间推出学生个人门票优惠活动，各类门票价格如下表：
某慈善单位欲购买三种类型的门票共张奖励品学兼优的留守学生，设购买种票张，种票张数是种票的倍还多张，种票张，根据以上信息解答下列问题：
（1）写出y与x之间的函数关系式；
（2）设购票总费用为元，求（元）与（张）之间的函数关系式；
（3）为方便学生游玩，计划购买学生的夜场票不低于张，且节假日通用票至少购买张，有哪几种购票方案？哪种方案费用最少？
26、（12分）如图，在正方形ABCD中，对角线AC与BD相交于点O，点E是BC上的一个动点，连接DE，交AC于点F．
（1）如图①，当时，求的值；
（2）如图②当DE平分∠CDB时，求证：AF＝OA；
（3）如图③，当点E是BC的中点时，过点F作FG⊥BC于点G，求证：CG＝BG．
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、B
【解析】
根据加权平均数的意义计算即可．
【详解】
解：小桐这学期的体育成绩：
95×20%+90×30%+86×50%=89（分），
故选：B．
本题考查了加权平均数：若n个数x1，x2，x3，…，xn的权分别是w1，w2，w3，…，wn，则（x1w1+x2w2+…+xnwn）÷（w1+w2+…+wn）叫做这n个数的加权平均数．
2、B
【解析】
根据角平分线的判定定理解答即可．
【详解】
如图所示，DE为点D到AB的距离．
∵DC＝DE，∠C＝90°，DE⊥AB，∴AD平分∠CAD，则点D在∠BAC的平分线上．
故选B．
本题考查了角平分线的判定，掌握到角的两边的距离相等的点在角的平分线上是解题的关键．
3、C
【解析】
试题分析：因为四边形ABCD是平行四边形，所以AB//CD,AB=CD，所以∠ABD=∠CDB,所以要使△ABE≌△CDF，
若添加条件：∠1=∠2，可以利用ASA证明△ABE≌△CDF，所以D正确，若添加条件：BE=FD，可以利用SAS证明△ABE≌△CDF，所以B正确，若添加条件：BF=DE，可以得到BE=FD，可以利用SAS证明△ABE≌△CDF，所以C正确；若添加条件：AE=CF，因为∠ABD=∠CDB,不是两边的夹角，所以不能证明△ABE≌△CDF，所以A错误，故选A.
考点：1.平行四边形的性质2.全等三角形的判定.
4、C
【解析】
∵四边相等的四边形一定是菱形，∴①正确；
∵顺次连接矩形各边中点形成的四边形一定是菱形，∴②错误；
∵对角线相等的平行四边形才是矩形，∴③错误；
∵经过平行四边形对角线交点的直线，一定能把平行四边形分成面积相等的两部分，∴④正确；
其中正确的有2个，故选C．
考点：中点四边形；平行四边形的性质；菱形的判定；矩形的判定与性质；正方形的判定．
5、B
【解析】
解：∵乙的11次射击成绩不都一样，∴a≠1．∵乙是成绩最稳定的选手，∴乙的方差最小，∴a的值可能是1.121．故选B．
6、D
【解析】
设房价定为x元，根据利润＝房价的净利润×入住的房间数可得．
【详解】
设房价定为x元，根据题意，得
故选：D．
此题考查了由实际问题抽象出一元二次方程，解题的关键是理解题意找到题目蕴含的相等关系．
7、B
【解析】
由四边形ABCD是平行四边形，根据平行四边形的对角相等，可得∠D=∠B=55°，又因为AE⊥CD，可得∠DAE=180°-∠D-∠AED=35°．
【详解】
解：∵四边形ABCD是平行四边形，
∴∠D=∠B=55°，
∵AE⊥CD，
∴∠AED=90°，
∴∠DAE=180°-∠D-∠AED=35°．
故选：B．
本题考查了平行四边形的性质：平行四边形的对角相等，还考查了垂直的定义与三角形内角和定理．题目比较简单，解题时要细心．
8、A
【解析】
根据加权平均数的定义列式计算可得．
【详解】
解：小明最终的成绩是70×50%+50×30%+80×20%=66（分），
故选：A．
本题考查了加权平均数的计算，加权平均数：（其中w1、w2、……、wn分别为x1、x2、……、xn的权）． 数据的权能反映数据的相对“重要程度”，对于同样的一组数据，若权重不同，则加权平均数很可能是不同的．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（a+2）（a﹣2）．
【解析】
试题分析：直接利用平方差公式分解因式a2﹣4=（a+2）（a﹣2）．故答案为（a+2）（a﹣2）．
【考点】因式分解-运用公式法．
10、3x（x+2）（x﹣2）
【解析】
先提公因式3x，然后利用平方差公式进行分解即可．
【详解】
3x3﹣12x
=3x（x2﹣4）
=3x（x+2）（x﹣2），
故答案为3x（x+2）（x﹣2）．
本题考查了提公因式法与公式法分解因式，要求灵活使用各种方法对多项式进行因式分解，一般来说，如果可以先提取公因式的要先提取公因式，再考虑运用公式法分解．
11、2.
【解析】
根据异分母分式加减法法则将进行变形，继而由原等式恒成立得到关于A、B的方程组，解方程组即可得.
【详解】
，
又∵
∴，
解得，
∴A+B＝2，
故答案为：2.
本题考查了分式的加减法，恒等式的性质，解二元一次方程组，得到关于A、B的方程组是解题的关键.
12、y=x+2 1
【解析】
一次函数y=kx+b的图象经过A、B两点，即A（2，1），B（0，2），代入可求出函数关系式．再根据三角形的面积公式，得出△AOC的面积．
【详解】
解：一次函数y=kx+b的图象经过A、B两点，即A（2，1），B（0，2），
与x轴交于点C（-2，0），
根据一次函数解析式的特点，可得出方程组，解得
则此一次函数的解析式为y=x+2，
△AOC的面积=|-2|×1÷2=1．
则此一次函数的解析式为y=x+2，△AOC的面积为1．
故答案为：y=x+2；1．
本题考查的是待定系数法求一次函数的解析式，解答本题的关键是掌握点在函数解析式上，点的横纵坐标就适合这个函数解析式．
13、
【解析】
二次根式有意义，就隐含条件b>1，由ab＜1，先判断出a、b的符号，再进行化简即可．
【详解】
若ab＜1，且代数式有意义；
故有b＞1，a＜1；
则代数式=|a|=-a．
故答案为：-a．
本题主要考查二次根式的化简方法与运用：当a＞1时，=a；当a＜1时，=-a；当a=1时，=1．
三、解答题（本大题共5个小题，共48分）
14、（1）①见解析；②，；（2）安排运往，，三地的产品件数分别为40件、80件，80件时，运费最少.
【解析】
（1）①根据运往B地的产品件数=总件数-运往A地的产品件数-运往B地的产品件数；运费=相应件数×一件产品的运费，即可补全图表；
②根据题意列出函数解析式即可；
（2）根据运往B地的件数不多于运往C地的件数，列出不等式，利用一次函数的性质解答即可；
【详解】
解：（1）①根据信息填表
②由题意列式（且是整数）（取值范围1分，没写是整数不扣分）
（2）若运往地的产品数量不超过运往地的数量则：，解得，
由，
∵，
∴随的增大而增大，
∴当时，最小，.
此时，.
所以安排运往，，三地的产品件数分别为40件、80件，80件时，运费最少.
考查了一次函数的应用，解题的关键是读懂题意，找出之间的数量关系，列出解析式．
15、（1）详见解析；（2）
【解析】
（1）过点P作PG⊥BC于G，过点P作PH⊥DC于H，如图1．要证PB=PE，只需证到△PGB≌△PHE即可；
（2）连接BD，如图2．易证△BOP≌△PFE，则有BO=PF，只需求出BO的长即可．
【详解】
证明:过点作于点，于点
是对角线上的动点
，
∠GPC+∠CPE= 90°
（2）连接BD，如图2．
∵四边形ABCD是正方形，
∴∠BOP=90°．
∵PE⊥PB即∠BPE=90°，
∴∠PBO=90°-∠BPO=∠EPF．
∵EF⊥PC即∠PFE=90°，
∴∠BOP=∠PFE．
在△BOP和△PFE中，
，
∴△BOP≌△PFE（AAS），
∴BO=PF．
∵四边形ABCD是正方形，
∴OB=OC，∠BOC=90°，
∴BC=OB．
∵BC=2，
∴OB=，
∴PF=．
本题主要考查了正方形的性质、等腰三角形的性质、全等三角形的判定与性质等知识，有一定的综合性，而通过添加辅助线证明三角形全等是解决本题的关键．
16、（1）四边形是矩形，理由见解析；（2）.
【解析】
（1）由菱形的性质可证明∠BOA=90°，然后再证明四边形AEBO为平行四边形，从而可证明四边形AEBO是矩形；
（2）依据矩形的性质可得到OE=AB，然后依据菱形的性质可得到AB=CD，即可求出的长.
【详解】
解：（1）四边形是矩形
理由如下：∵，，
∴四边形是平行四边形
又∵菱形对角线交于点，∴，即
∴四边形是矩形
（2）∵四边形是矩形，
∴
在菱形中，
∴.
本题主要考查的是菱形的性质判定、矩形的性质和判定，求出四边形是矩形是解题的关键．
17、（1）答案见详解；（1），；（3）1．
【解析】
（1）如图1中，根据平行四边形的定义，画出第为5，高为3的平行四边形即可．
（1）如图1中，根据菱形的判定画出图形即可．
（3）根据矩形的定义画出图形即可．
【详解】
解：（1）如图1中，平行四边形即为所求；
（1）如图1中，菱形即为所求．，，
故答案为，；
（3）如图3中，矩形即为所求，；
故答案为1．
本题考查勾股定理，菱形的性质，矩形的性质等知识，熟练掌握基本知识是解题的关键．
18、（1）作图见解析，；（2）作图见解析，
【解析】
（1）分别将A、B、C三个点向右平移五个单位得到对应点，顺次连接即可得，再写出坐标即可；
（2）分别作出A、B、C三个点关于x轴的对称点，顺次连接即可得，再写出坐标即可．
【详解】
（1）如图所示，即为所求，；
（2）如图所示，即为所求，．
本题考查坐标系中的平移与轴对称作图，熟练掌握坐标系中点的平移与对称规律是解题的关键．
一、填空题（本大题共5个小题，每小题4分，共20分）
19、5.3
【解析】
(4×10+5×20+6×15+7×5) ÷50=5.3(小时).
故答案为5.3.
20、 (0，﹣)
【解析】
根据在y轴上点的坐标特征，可知要求直线y＝x﹣与y轴的交点坐标就是令x=0
【详解】
∵当x＝0时，y＝×0﹣＝﹣，
∴与y轴的交点坐标是(0，﹣)，
故答案为：(0，﹣)．
本题考查了一次函数与y轴的交点坐标的求法，正确理解知识是解题的关键.
21、40
【解析】
根据方位角的概念，画图正确表示出行驶的过程，再根据已知转向的角度结合三角形的内角和与外角的关系求解．
【详解】
如图，A沿北偏东60°的方向行驶到B，则∠BAC=90°-60°=30°，
B沿南偏西20°的方向行驶到C，则∠BCO=90°-20°=70°，
又∵∠ABC=∠BCO-∠BAC，∴∠ABC=70°-30°=40°．
故答案为：40°
解答此类题需要从运动的角度，正确画出方位角，再结合三角形的内角和与外角的关系求解．
22、1．
【解析】
试题分析：∵直角三角形的两条直角边长为6，8，∴由勾股定理得，斜边=10.
∴斜边上的中线长=×10=1．
考点：1.勾股定理；2. 直角三角形斜边上的中线性质．
23、1
【解析】
分析：根据频率= 或频数=频率×数据总和解答．
详解：由题意，该组的人数为：400×0.25=1（人）．
故答案为1．
点睛：本题考查了频数与频率之间的计算，熟知频数、频率及样本总数之间的关系是解决本题的关键．
二、解答题（本大题共3个小题，共30分）
24、感知：见解析；探究：见解析；应用： ．
【解析】
感知：先判断出∠ABC=∠CBF=90°，AB=BC，进而判断出BE=BF，得出△ABE≌△CBF（SAS）即可得出结论；
探究：先判断出∠ABE=∠CBF，进而得出△ABE≌△CBF（SAS），即可得出结论；
应用：先求出CF=1，再判断出∠CFE=90°，利用勾股定理即可得出结论．
【详解】
解：感知：∵四边形ABCD是正方形，
∴∠ABC=∠CBF=90°，AB=BC，
∵△BEF是等腰直角三角形，
∴BE=BF，
∴△ABE≌△CBF（SAS），
∴∠AEB=∠CFB；
探究：∵四边形ABCD是正方形，
∴AB=BC，∠ABC=90°，
∵△BEF是等腰直角三角形，
∴BE=BF，∠EBF=90°=∠ABC，
∴∠ABE=∠CBF，
∴△ABE≌△CBF（SAS），
∴∠AEB=∠CFB；
应用：由（2）知，△ABE≌△CBF，∠BFC=∠BEA，
∴CF=AE=1，
∵△BEF是等腰直角三角形，
∴∠BFE=∠BEF=45°，
∴∠AEB=135°，
∴∠BFC=135°，
∴∠CFE=∠BFC-∠BFE=90°，
在Rt△CFE中，CF=1，EF=2，根据勾股定理得， ，
故答案为：．
此题是四边形综合题，主要考查了正方形的性质，等腰直角三角形的性质，全等三角形的判定和性质，勾股定理，判断出△ABE≌△CBF（SAS），是解本题的关键．
25、（1）；（2）；（3）共有种购票方案：；；；当种票为张，种票张，种票为张时费用最少，最少费用元.
【解析】
（1）根据三种门票共购买100张，即可找出x与y之间的函数关系式；
（2）根据购票总费用=30×购买A种票数量+50×购买B种票数量+80×购买C种票数量，即可找出W（元）与x（张）之间的函数关系式；
（3）根据购买A种票不低于24张、C种票至少5张，即可得出关于x的一元一次不等式组，解之即可得出x的取值范围，再利用一次函数的性质即可解决最值问题．
【详解】
解：根据题意，
所以

依题意得
解得
因为整数为
所以共有种购票方案,分别为
；
；
而
因为
所以随的增大而减小，
所以当时，
即当种票为张，种票张，种票为张时费用最少，最少费用元
本题考查了一次函数的应用以及一元一次不等式组的应用，解题的关键是：（1）根据三种门票共购买100张，找出y与x之间的函数关系式；（2）根据购票总费用=30×购买A种票数量+50×购买B种票数量+80×购买C种票数量，找出W与x之间的函数关系式；（3）根据购买A、C两种门票张数的范围，列出关于x的一元一次不等式．
26、（1）；（2）（3）见解析
【解析】
试题分析：（1）利用相似三角形的性质求得与的比值，依据和同高，则面积的比就是与的比值，据此即可求解；
（2）利用三角形的外角和定理证得 可以证得，在直角中，利用勾股定理可以证得；
（3）连接 易证是的中位线，然后根据是等腰直角三角形，易证 利用相似三角形的对应边的比相等即可．
试题解析：(1)∵，∴
∵四边形ABCD是正方形，

∴△CEF∽△ADF，∴，∴，∴；
(2)证明：∵DE平分∠CDB,
∴∠ODF=∠CDF，
∵AC、BD是正方形ABCD的对角线．

而∠ADF=∠ADO+∠ODF，∠AFD=∠FCD+∠CDF，
∴∠ADF=∠AFD，
∴AD=AF，
在中,根据勾股定理得：
AD==OA，

(3)证明：连接OE.
∵点O是正方形ABCD的对角线AC、BD的交点，
点O是BD的中点．
又∵点E是BC的中点，
∴OE是△BCD的中位线，


∴=，∴.


.在 中，∵∠GCF=45°.∴CG=GF，
又∵CD=BC，∴，
∴=.
∴CG=BG.
题号
一
二
三
四
五
总分
得分
选手
甲
乙
丙
平均数
9.3
9.3
9.3
方差
0.026
a
0.032
地
地
地
产品件数（件）
运费（元）
时间（时）
4
5
6
7
人数
10
20
15
5
地
地
地
产品件数（件）
运费（元）