中职数学高教版（2021·十四五）基础模块 上册3.3 函数的性质教课内容ppt课件

这是一份中职数学高教版（2021·十四五）基础模块 上册3.3 函数的性质教课内容ppt课件，共54页。PPT课件主要包含了函数的单调性，函数的奇偶性，几种常见的函数等内容，欢迎下载使用。

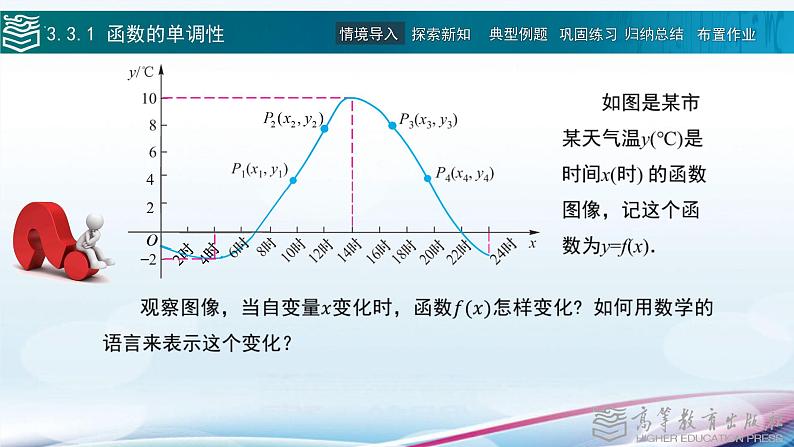
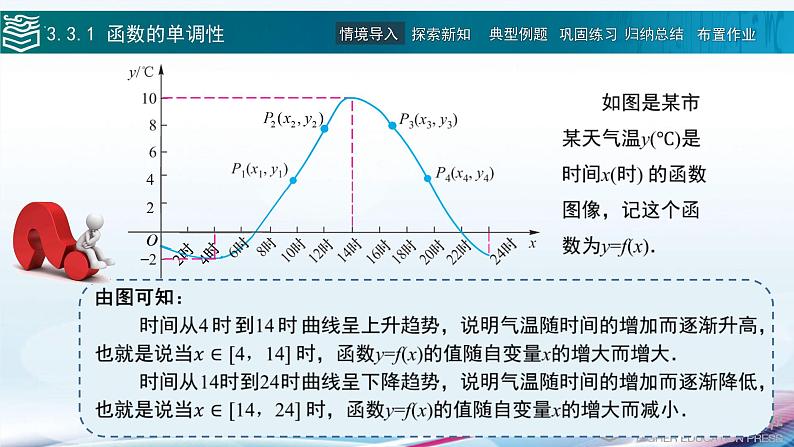
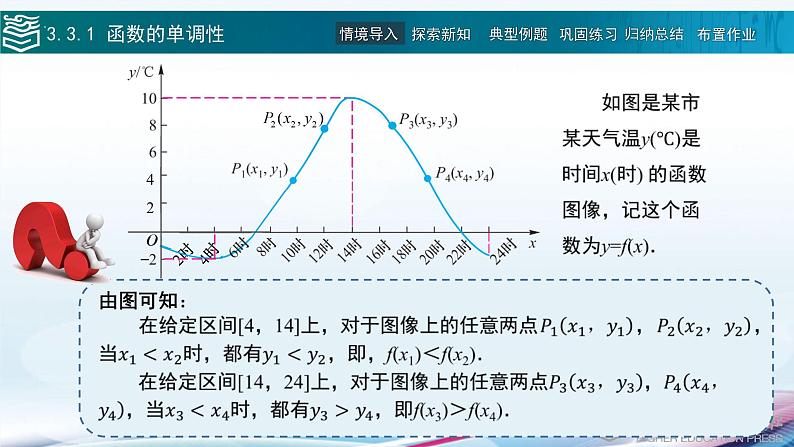
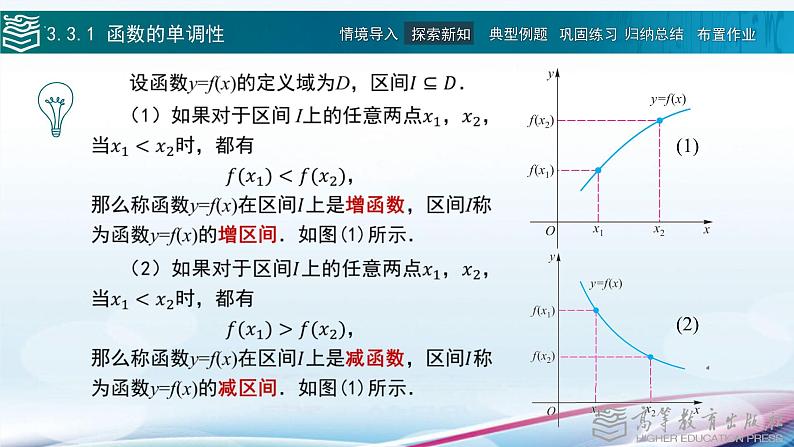
函数是描述客观事物运动变化规律的数学模型．了解了函数的变化规律，也就基本把握了相应事物的变化规律，因此这一节我们来研究函数性质．
例1 根据函数在R上的图像，如图所示，写出其单调区间．
例1 根据函数在R上的图像，如图所示，写出其单调区间：
大千世界，美无处不在，展示了生活中的对称之美．
数学中也存在着对称美，函数图像的对称就是其中一种．
观察这两种对称的函数图像，当自变量互为相反数时，它们对应的函数值有什么关系？
如果一个函数是奇函数或偶函数，就说这个函数具有奇偶性，其定义域一定关于原点中心对称．
有没有某个函数，它既是奇函数又是偶函数？如果有，请举例说明．
3.3.2 函数的奇偶性
回顾义务教育阶段学过的一次函数、反比例函数与二次函数，它们的定义域、值域、单调性、奇偶性等各是怎样的呢？如何用数学的语言表达？
例6 函数y=(3m+4)x+m在R上是减函数．（1）求m的取值范围；（2）若函数的图像过点(-1，0)，试求图像与y轴的交点坐标．
（2）由于y=(3m+4)x+m的图像过点(-1，0)，则有0=(3m+4)×(-1)x+m解得，m =-2．所以函数的解析式为y=-2x-2 ． 令x=0，得y=-2故函数的图像与y轴的交点坐标为(0，-2)．
对二次函数进行总结，见表：
1．若函数f(x)=(2a-1)x(a为实数)在R上是增函数，则（ ）．A. B. C. D.