2024-2025学年安徽省临泉数学九年级第一学期开学调研模拟试题【含答案】

这是一份2024-2025学年安徽省临泉数学九年级第一学期开学调研模拟试题【含答案】，共23页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）在平面直角坐标系中，一次函数与的图像互相平行，如果这两个函数的部分自变量和对应的函数值如下表所示：
那么的值是（ ）
A．B．C．D．
2、（4分）一个多边形的内角和比它的外角和的3倍少180°，则这个多边形的边数为( )
A．5B．6C．7D．8
3、（4分）如图，正方形纸片ABCD的边长为4 cm，点M、N分别在边AB、CD上．将该纸片沿MN折叠，使点D落在边BC上，落点为E，MN与DE相交于点Q．随着点M的移动，点Q移动路线长度的最大值是（ ）
\
A．2 cmB．4 cmC． cmD．1 cm
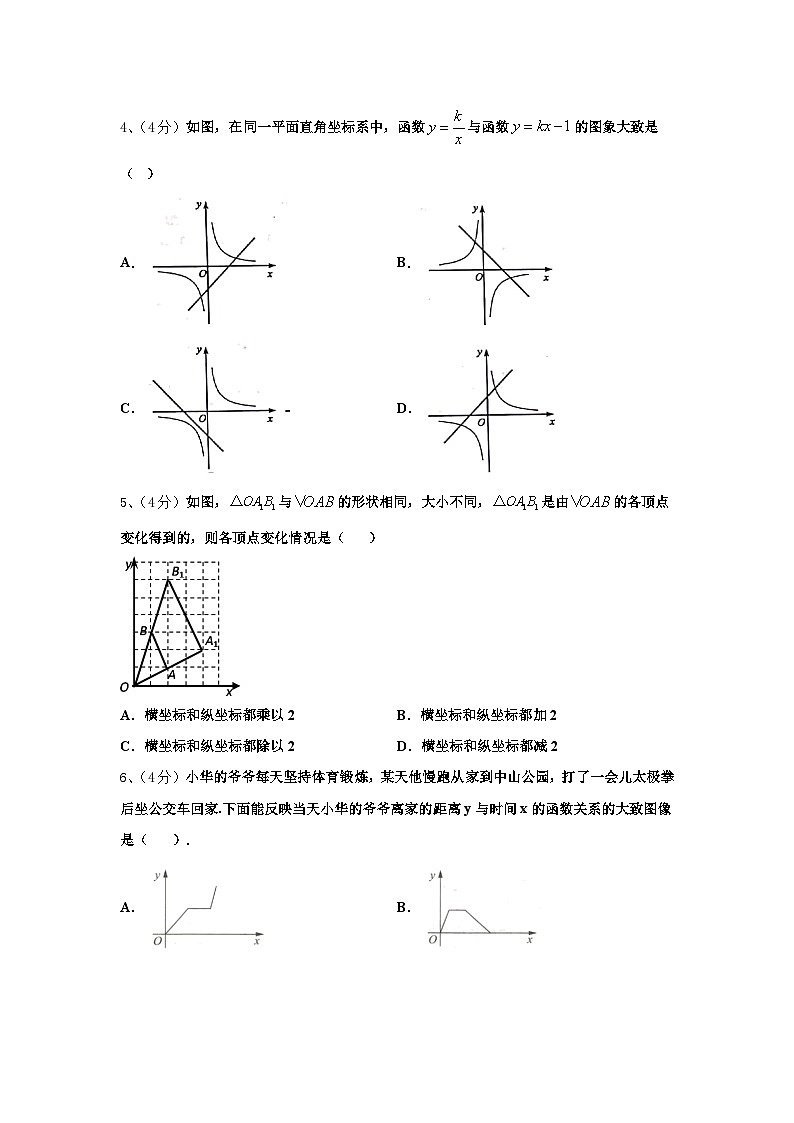
4、（4分）如图，在同一平面直角坐标系中，函数与函数的图象大致是（ ）
A．B．
C．D．
5、（4分）如图，与的形状相同，大小不同，是由的各顶点变化得到的，则各顶点变化情况是（ ）
A．横坐标和纵坐标都乘以2B．横坐标和纵坐标都加2
C．横坐标和纵坐标都除以2D．横坐标和纵坐标都减2
6、（4分）小华的爷爷每天坚持体育锻炼，某天他慢跑从家到中山公园，打了一会儿太极拳后坐公交车回家.下面能反映当天小华的爷爷离家的距离y与时间x的函数关系的大致图像是（ ）.
A．B．C．D．
7、（4分）如图，一块等腰直角的三角板，在水平桌面上绕点按顺时针方向旋转到的位置，使三点共线，那么旋转角度的大小为( )
A．B．C．D．
8、（4分）菱形的周长为20cm，两个相邻的内角的度数之比为1：2，则较长的对角线的长度是( )
A．cmB．cmC．cmD．5cm
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）若a，b都是实数，b＝+﹣2，则ab的值为_____．
10、（4分）如图，直线分别与轴、轴交于点,点是反比例函数的图象上位于直线下方的点，过点分别作轴、轴的垂线，垂足分别为点,交直线于点,若,则的值为__________．
11、（4分）如图，“今有直角三角形，勾(短直角边)长为5，股(长直角边)长为12，河该直角三角形能容纳的如图所示的正方形边长是多少?”，该问题的答案是______．
12、（4分）如果一次函数y＝kx+2的函数值y随着x的值增大而减小，那么k的取值范围是_____．
13、（4分）函数y=中，自变量x的取值范围是______．
三、解答题（本大题共5个小题，共48分）
14、（12分）在社会主义新农村建设中，衢州某乡镇决定对A、B两村之间的公路进行改造，并有甲工程队从A村向B村方向修筑，乙工程队从B村向A村方向修筑．已知甲工程队先施工3天，乙工程队再开始施工．乙工程队施工几天后因另有任务提前离开，余下的任务有甲工程队单独完成，直到公路修通．下图是甲乙两个工程队修公路的长度y（米）与施工时间x（天）之间的函数图象，请根据图象所提供的信息解答下列问题：
（1）乙工程队每天修公路多少米？
（2）分别求甲、乙工程队修公路的长度y（米）与施工时间x（天）之间的函数关系式．
（3）若该项工程由甲、乙两工程队一直合作施工，需几天完成？
15、（8分）先化简,再求值: ，其中．
16、（8分）（1）解方程：x2+3x-4=0 (2) 计算：
17、（10分）已知：如图，在▱ABCD中，AE⊥BC，CF⊥AD，垂足分别为E、F，AE、CF分别与BD相交于点G、H，联结AH、CG．
求证：四边形AGCH是平行四边形．
18、（10分）如图1．在边长为10的正方形中，点在边上移动（点不与点，重合），的垂直平分线分别交，于点，，将正方形沿所在直线折叠，则点的对应点为点，点落在点处，与交于点，

（1）若，求的长；
（2）随着点在边上位置的变化，的度数是否发生变化？若变化，请说明理由；若不变，请求出的度数；
（3）随着点在边上位置的变化，点在边上位置也发生变化，若点恰好为的中点（如图2），求的长．
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）在平面直角坐标系中，已知一次函数y=x+1的图象经过P1（x1，y1）、P2（x2，y2）两点，若x1＜x2，则y1_____y2（填“＞”，“＜”或“=”）.
20、（4分）正n边形的一个外角的度数为60°，则n的值为 ．
21、（4分）如图，在△ABC中，AB=BC=4，AO=BO，P是射线CO上的一个动点，∠AOC=60°，则当△PAB为直角三角形时，AP的长为 ．
22、（4分）函数的自变量的取值范围是 ．
23、（4分）某商场品牌手机经过5、6月份连续两次降价，每部售价由5000元降到4050元，设平均每次降价的百分率为x，根据题意可列方程：_____．
二、解答题（本大题共3个小题，共30分）
24、（8分）如图，在▱ABCD中，点E、F在BD上，且BF＝DE．
（1）写出图中所有你认为全等的三角形；
（2）延长AE交BC的延长线于G，延长CF交DA的延长线于H（请补全图形），证明四边形AGCH是平行四边形．
25、（10分）已知一次函数的图象经过（2，5）和（﹣1，﹣1）两点．
（1）求这个一次函数的解析式；
（2）在给定的直角坐标系xOy中画出这个一次函数的图象，并指出当x增大时，y如何变化？
26、（12分）为声援扬州“运河申遗”，某校举办了一次运河知识竞赛，满分10分，学生得分为整数，成绩达到6分以上（包括6分）为合格，达到9分以上（包含9分）为优秀．这次竞赛中甲乙两组学生成绩分布的条形统计图如图所示．
（1）补充完成下面的成绩统计分析表：
（2）小明同学说：“这次竞赛我得了7分，在我们小组中排名属中游略偏上！”观察上表可知，小明是 组的学生；（填“甲”或“乙”）
（3）甲组同学说他们组的合格率、优秀率均高于乙组，所以他们组的成绩好于乙组．但乙组同学不同意甲组同学的说法，认为他们组的成绩要好于甲组．请你给出两条支持乙组同学观点的理由．
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、A
【解析】
由一次函数y2=k2x+b2与y2=k2x+b2的图象互相平行，得出k2=k2，设k2=k2=a，将（m，-2）、（0，0）代入y2=ax+b2，得到am=-2；将（m，2）、（0，n）、（2，7）代入y2=ax+b2，解方程组即可求出m的值．
【详解】
解：∵一次函数y2=k2x+b2与y2=k2x+b2的图象互相平行，
∴k2=k2，
设k2=k2=a，则y2=ax+b2，y2=ax+b2．
将（m，-2）、（0，0）代入y2=ax+b2，得am=-2①；
将（m，2）、（0，n）、（2，7）代入y2=ax+b2，
得am+n=2②，2a+n=7③，
①代入②，得n=3，
把n=3代入③，得a=2，
把a=2代入①，得m=-2．
故选：A．
本题考查了两条直线的平行问题：若两条直线是平行的关系，那么他们的自变量系数相同，即k值相同．即若直线y2=k2x+b2与直线y2=k2x+b2平行，那么k2=k2．也考查了一次函数图象上点的坐标特征．难度适中．
2、C
【解析】
解答本题的关键是记住多边形内角和公式为（n-2）×180°，任何多边形的外角和是360度．外角和与多边形的边数无关．
【详解】
多边形的内角和可以表示成（n-2）•180°，外角和是固定的360°，从而可根据内角和比他的外角和的3倍少180°列方程求解．
设所求n边形边数为n，
则（n-2）•180°=360°×3-180°，
解得n=7，
故选C．
本题主要考查了多边形的内角和与外角和，解答本题的关键是记住多边形内角和公式为（n-2）×180°.
3、A
【解析】
如图，取AB，CD的中点K，G，连接KG，BD交于点O，由题意知，点Q运动的路线是线段OG，因为DO=OB，所以DG=GC，所以OG=BC=×4=2，所以点Q移动路线的最大值是2，故选A.
4、A
【解析】
分情况讨论：和时，根据图像的性质，即可判定.
【详解】
当时，函数的图像位于第一、三象限，函数的图像第一、三、四象限；
当时，函数的图像位于第二、四象限，函数的图像第二、三、四象限；
故答案为A.
此题主要考查一次函数和反比例函数的性质，熟练掌握，即可解题.
5、A
【解析】
根据题意得：△OAB∽△OAB，然后由相似三角形的对应边成比例，求得答案．
【详解】
根据题意得：△O AB∽△OAB，
∵O(0,0),A(2,1),B(1,3),B点的坐标为(2,6)，A(4,2)
∴横坐标和纵坐标都乘以2.
故选A.
此题考查坐标与图形性质，相似三角形的性质，解题关键在于利用相似三角形的对应边成比例
6、C
【解析】
根据在每段中，离家的距离随时间的变化情况即可进行判断．
【详解】
图象应分三个阶段，第一阶段：慢步到离家较远的绿岛公园，在这个阶段，离家的距离随时间的增大而增大；第二阶段：打了一会儿太极拳，这一阶段离家的距离不随时间的变化而改变。故D错误；第三阶段：搭公交车回家，这一阶段，离家的距离随时间的增大而减小，故A错误，并且这段的速度大于第一阶段的速度，则B错误.
故选：C.
本题考查函数图象，解题的关键是由题意将图象分为三个阶段进行求解.
7、D
【解析】
根据三点共线可得，再根据等腰直角三角板的性质得，即可求出旋转角度的大小．
【详解】
∵三点共线
∴
∵这是一块等腰直角的三角板
∴
∴
故旋转角度的大小为135°
故答案为：D．
本题考查了三角板的旋转问题，掌握等腰直角三角板的性质、旋转的性质是解题的关键．
8、B
【解析】
如图所示：
∵菱形的周长为20cm，
∴菱形的边长为5cm，
∵两邻角之比为1:2，
∴较小角为60°，
∴∠ABO=30°，AB=5cm，
∵最长边为BD,BO=AB⋅cs∠ABO=5×= (cm)，
∴BD=2BO= (cm).
故选B.
二、填空题（本大题共5个小题，每小题4分，共20分）
9、1
【解析】
直接利用二次根式有意义的条件得出a的值，进而利用负指数幂的性质得出答案．
【详解】
解：∵b＝+﹣2，
∴
∴1-2a=0，
解得：a=，则b=-2，
故ab=（）-2=1．
故答案为1．
此题主要考查了二次根式有意义的条件，以及负指数幂的性质，正确得出a的值是解题关键．
10、-3
【解析】
首先设PN=x，PM=y，由已知条件得出EE′=PN=x，FF′=PM=y，A（-5,0），B（0,5），通过等量转换，列出关系式，求出，又因为反比例函数在第二象限，进而得解.
【详解】
过点F作FF′⊥OA与F′，过点E作EE′⊥OB与E′，如图所示，
设PN=x，PM=y，
由已知条件，得
EE′=PN=x，FF′=PM=y，A（-5,0），B（0,5）
∴OA=OB=5
∴∠OAB=∠OBA=45°
∴FF′=AF′=y，EE′=BE′=x，
∴AF=，BE=
又∵
∴
∴
又∵反比例函数在第二象限，
∴.
此题主要考查一次函数和反比例函数的综合应用，熟练掌握，即可解题.
11、
【解析】
根据锐角三角函数的定义以及正方形的性质即可求出答案．
【详解】
解：设正方形的边长为x，
∴CE=ED=x，
∴AE=AC-CE=12-x，
在Rt△ABC中，
，
在Rt△ADE中，
，
∴，
∴解得：x=，
故答案为：.
本题考查三角形的综合问题，解题的关键是熟练运用锐角三角函数的定义以及正方形的性质，本题属于中等题型．
12、k＜1．
【解析】
根据一次函数的性质解答即可.
【详解】
∵一次函数y＝kx+2，函数值y随x的值增大而减小，
∴k＜1．
故答案为：k＜1．
本题考查了一次函数的图像与性质，对于一次函数y=kx+b（k为常数，k≠1）,当k>1时，y随x的增大而增大；当k<1时，y随x的增大而减小.
13、x≠1
【解析】
根据分母不能为零，可得答案．
【详解】
解：由题意，得x-1≠0，
解得x≠1，
故答案为：x≠1．
本题考查了函数自变量的取值范围，利用分母不能为零得出不等式是解题关键．
三、解答题（本大题共5个小题，共48分）
14、（1）120米（2）y乙=120x﹣1，y甲=60x（3）2
【解析】
解：（1）由图得：720÷（2﹣3）=120（米），
答：乙工程队每天修公路120米．
（2）设y乙=kx+b，则，解得：．∴y乙=120x﹣1．
当x=6时，y乙=1．
设y甲=kx，则1=6k，k=60，∴y甲=60x．
（3）当x=15时，y甲=200，∴该公路总长为：720+200=1620（米）．
设需x天完成，由题意得：
（120+60）x=1620，解得：x=2．
答：该项工程由甲、乙两工程队一直合作施工，需2天完成
（1）根据图形用乙工程队修公路的总路程除以天数，即可得出乙工程队每天修公路的米数．
（2）根据函数的图象运用待定系数法即可求出y与x之间的函数关系式．
（3）先求出该公路总长，再设出需要x天完成，根据题意列出方程组，求出x，即可得出该项工程由甲、乙两工程队一直合作施工，需要的天数．
15、，1
【解析】
先根据完全平方公式、平方差公式和单项式乘多项式法则化简原式，再将x的值代入计算可得．
【详解】
解：
当x=-2时，原式=24-1=1．
本题主要考查整式的混合运算-化简求值，解题的关键是掌握完全平方公式、平方差公式和单项式乘多项式法则．
16、（1） （2）
【解析】
（1）解一元二次方程,将等式左边因式分解，转化成两个一元一次方程，求解即可. (2) 首先把特殊角的三角函数值代入，然后进行二次根式的运算即可．
【详解】
解：（1）原方程变形得（x-1）(x+4)=0
解得x1=1，x2=-4
经验：x1=1，x2=-4是原方程的解.
(2)原式=×××=
本题是计算题第（1）考查解二元一次方程-因式分解．（2）特殊三角函数的值．本题较基础，熟练掌握运算的方法即可求解.
17、证明见解析.
【解析】
法1：由平行四边形对边平行，且CF与AD垂直，得到CF与BC垂直，根据AE与BC垂直，得到AE与CF平行，得到一对内错角相等，利用等角的补角相等得到∠AGB=∠DHC，根据AB与CD平行，得到一对内错角相等，再由AB=CD，利用AAS得到三角形ABG与三角形CDH全等，利用全等三角形对应边相等得到AG=CH，利用一组对边平行且相等的四边形为平行四边形即可得证；
法2：连接AC，与BD交于点O，利用平行四边形的对角线互相平分得到OA=OC，OB=OD，再由AB与CD平行，得到一对内错角相等，根据CF与AD垂直，AE与BC垂直，得一对直角相等，利用ASA得到三角形ABG与三角形CDH全等，利用全等三角形对应边相等得到BG=DH，根据等式的性质得到OG=OH，利用对角线互相平分的四边形为平行四边形即可得证．
证明：在□ABCD中，AD∥BC，AB∥CD，
∵CF⊥AD，∴CF⊥BC，
∵AE⊥BC，∴AE∥CF，即AG∥CH，∴∠AGH=∠CHG，
∵∠AGB=180°﹣∠AGH，∠DHC=180°﹣∠CHG，
∴∠AGB=∠DHC，
∵AB∥CD，∴∠ABG=∠CDH，∴△ABG≌CDH，
∴AG=CH，
∴四边形AGCH是平行四边形；
法2：连接AC，与BD相交于点O，
在□ABCD中，AO=CO，BO=DO，∠ABE=∠CDF，AB∥CD，
∴∠ABG=∠CDH，
∵CF⊥AD，AE⊥BC，
∴∠AEB=∠CFD=90°，
∴∠BAG=∠DCH，
∴△ABG≌CDH，
∴BG=DH，
∴BO﹣BG=DO﹣DH，
∴OG=OH，
∴四边形AGCH是平行四边形．
“点睛”此题考查了平行四边形的判定与性质，熟练掌握平式子变形的判定与性质是解本题的关键.
18、（1）；（2）不变，45°；（3） ．
【解析】
（1）由翻折可知：EB=EM，设EB=EM=x，在Rt△AEM中，根据EM2=AM2+AE2，构建方程即可解决问题．
（2）如图1-1中，作BH⊥MN于H．利用全等三角形的性质证明∠ABM=∠MBH，∠CBP=∠HBP，即可解决问题．
（3）如图2中，作FG⊥AB于G．则四边形BCFG是矩形，FG=BC，CF=BG．设AM=x，在Rt△DPM中，利用勾股定理构建方程求出x，再在Rt△AEM中，利用勾股定理求出BE，EM，AE，再证明AM=EG即可解决问题．
【详解】
（1）如图1中，
∵四边形ABCD是正方形，
∴∠A=90°，AB=AD=10，
由翻折可知：EB=EM，设EB=EM=x，
在Rt△AEM中，∵EM2=AM2+AE2，
∴x2=42+（10-x）2，
∴x=．
∴BE=．
（2）如图1-1中，作BH⊥MN于H．
∵EB=EM，
∴∠EBM=∠EMB，
∵∠EMN=∠EBC=90°，
∴∠NMB=∠MBC，
∵AD∥BC，
∴∠AMB=∠MBC，
∴∠AMB=∠BMN，
∵BA⊥MA，BH⊥MN，
∴BA=BH，
∵∠A=∠BHM=90°，BM=BM，BA=BH，
∴Rt△BAM≌△BHM（HL），
∴∠ABM=∠MBH，
同法可证：∠CBP=∠HBP，
∵∠ABC=90°，
∴∠MBP=∠MBH+∠PBH=∠ABH+∠CBH=∠ABC=45°．
∴∠PBM=45°．
（3）如图2中，作FG⊥AB于G．则四边形BCFG是矩形，FG=BC，CF=BG．设AM=x，
∵PC=PD=5，
∴PM+x=5，DM=10-x，
在Rt△PDM中，（x+5）2=（10-x）2+25，
∴x=，
∴AM=，
设EB=EM=m，
在Rt△AEM中，则有m2=（10-m）2+（）2，
∴m= ，
∴AE=10-，
∵AM⊥EF，
∴∠ABM+∠GEF=90°，∠GEF+∠EFG=90°，
∴∠ABM=∠EFG，
∵FG=BC=AB，∠A=∠FGE=90°，
∴△BAM≌△FGE（AAS），
∴EG=AM= ，
∴CF=BG=AB-AE-EG=10- ．
此题考查四边形综合题、正方形的性质、全等三角形的判定和性质、勾股定理，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，学会利用参数构建方程解决问题．
一、填空题（本大题共5个小题，每小题4分，共20分）
19、
【解析】
根据一次函数的性质，k＞0时，y随x的增大而增大；k＜0时，y随x的增大而减小，从而得出答案.
【详解】
一次函数y=x+1，，y随x的增大而减小
∵x1＜x2
∴y1＞y2
故答案为：＞
本题考查了一次函数的增减性，熟练掌握相关知识点是解题关键.
20、1
【解析】
解：∵正n边形的一个外角的度数为10°，
∴n=310÷10=1．
故答案为：1．
21、1或1或1
【解析】
本题根据题意分三种情况进行分类求解，结合三角函数，等边三角形的性质即可解题.
【详解】
试题分析：当∠APB=90°时（如图1），
∵AO=BO，
∴PO=BO，
∵∠AOC=60°，
∴∠BOP=60°，
∴△BOP为等边三角形，
∵AB=BC=4，
∴；
当∠ABP=90°时（如图1），
∵∠AOC=∠BOP=60°，
∴∠BPO=30°，
∴，
在直角三角形ABP中，
，
如图3，∵AO=BO，∠APB=90°，
∴PO=AO，
∵∠AOC=60°，
∴△AOP为等边三角形，
∴AP=AO=1，
故答案为或或1．
考点：勾股定理．
22、x＞1
【解析】
解：依题意可得，解得，所以函数的自变量的取值范围是
23、5000(1﹣x)2＝1
【解析】
根据现在售价5000元月平均下降率现在价格1元，即可列出方程．
【详解】
解：设平均每次降价的百分率为x，根据题意可列方程：
5000(1﹣x)2＝1．
故答案为：5000(1﹣x)2＝1．
此题主要考查了由实际问题抽象出一元二次方程，关键是掌握增长率问题的计算公式：变化前的量为a，变化后的量为b，平均变化率为x，则经过两次变化后的数量关系为．
二、解答题（本大题共3个小题，共30分）
24、（1）△ABE≌△CDF；△AED≌△CFB；△ABD≌△CDB；（2）详见解析
【解析】
（1）因为ABCD是平行四边形，AD∥BC，因此∠ADE＝∠CBF，又知DE＝BF，D＝BC那么构成了三角形ADE和CBF全等的条件（SAS）因此△AED≌△CFB．同理可得出△ABE≌△CDF，△ABD≌△CDB．
（2）要证明四边形AGCH是个平行四边形，已知的条件有AB∥CD，只要证得AG∥CH即可得出上述结论．那么就需要证明∠AEB＝∠DFC，也就是证明△ABE≌△CDF，根据AB∥CD．∴∠ABD＝∠CDB．这两个三角形中已知的条件就有AB＝CD，BE＝DF（BE＝DF+EF＝DE+EF＝DF），又由上面得出的对应角相等，那么两三角形就全等了（SAS）．
【详解】
（1）解：△ABE≌△CDF；△AED≌△CFB；△ABD≌△CDB；
（2）证明：在△ADE和△CBF中，AD＝CB，∠ADE＝∠CBF，DE＝BF，
∴△ADE≌△CBF，
∴∠AED＝∠CFB．
∵∠FEG＝∠AED＝∠CFB＝∠EFH，
∴AG‖HC，而且，AH‖GC，
∴四边形AGCH是平行四边形
本题考查了全等三角形的判定，平行四边形的性质和判定等知识点，本题中公共全等三角形来得出线段和角相等是解题的关键．
25、y=2x+1；y随着x的增大而增大.
【解析】
（1）设一次函数解析式为y=kx+b，将已知两点坐标代入求出k与b的值，即可确定出解析式；
（2）做出函数图象，如图所示，根据增减性即可得到结果．
【详解】
解：（1）设一次函数解析式为y=kx+b，
将（2，5）与（﹣1，﹣1）代入得，
解得：k=2，b=1，
则一次函数解析式为y=2x+1；
（2）如图所示，y随着x的增大而增大．
此题考查了待定系数法求一次函数解析式，以及一次函数的图象，熟练掌握待定系数法是解本题的关键．
26、（1）6；7.1；（2）甲；（3）乙组的平均分，中位数高于甲组，方差小于甲组，故乙组成绩好于甲组
【解析】
（1）将甲组成绩按照从小到大的顺序排列，找出第5、6个成绩，求出平均数即为甲组的中位数；找出乙组成绩，求出乙组的平均分，填表即可：
∵甲组的成绩为：3，6，6，6，6，6，7，8，9，10，∴甲组中位数为6分
∵乙组成绩为5，5，6，7，7，8，8，8，8，9，平均分为（分）
（2）根据两组的中位数，观察表格，成绩为7分处于中游略偏上，应为甲组的学生．
（3）乙组的平均分高于甲组，中位数高于甲组，方差小于甲组，所以乙组成绩好于甲组
解：（1）填表如下：
（2）甲．
（3）乙组的平均分，中位数高于甲组，方差小于甲组，故乙组成绩好于甲组
故答案为（1）6；7.1；（2）甲
题号
一
二
三
四
五
总分
得分
组别
平均分
中位数
方差
合格率
优秀率
甲组
6.7
3.41
90%
20%
乙组
7.5
1.69
80%
10%
组别
平均分
中位数
方差
合格率
优秀率
甲组
6.7
6
3.41
90%
20%
乙组
7.1
7.5
1.69
80%
10%