鲁教版八年级数学上册期末素养综合测试(一)课件

这是一份鲁教版八年级数学上册期末素养综合测试(一)课件，共60页。

1.(跨学科·语文)(2024河南安阳期末)河南省地处中原,是中华 文明的发源地之一,积累了深厚的历史文化底蕴,位于开封的 朱仙镇被誉为中原小镇之首.以下是“中原小镇”四个字的 篆体,其中可以看成中心对称图形的是 (　    )
一、选择题(每小题3分,共36分)
A B C D
解析　选项A、B、D中的图形都不能找到一个点,使图形绕 该点旋转180°后与原来的图形重合,所以不是中心对称图形; 选项C中的图形能找到一个点,使图形绕该点旋转180°后与 原来的图形重合,所以是中心对称图形.故选C.
2.(2023山东东营期末)下列等式从左到右的变形中,属于因 式分解的是 (　    )A.a2+1=a  B.x2-2x+1=x(x-2)+1C.4m3n=4m3·n D.m2+5m=m(m+5)
解析　A选项,等号右边不是整式的积的形式,不是因式分解; B选项,等号右边不是整式的积的形式,不是因式分解;C选项, 等号左边不是多项式,不是因式分解;D选项,是因式分解.故 选D.
3.下列分式是最简分式的是 (　    )A.　　　 B. 　　C. 　　D. 
解析　A. = ;B. 是最简分式;C. = = ;D. = = .故选B.
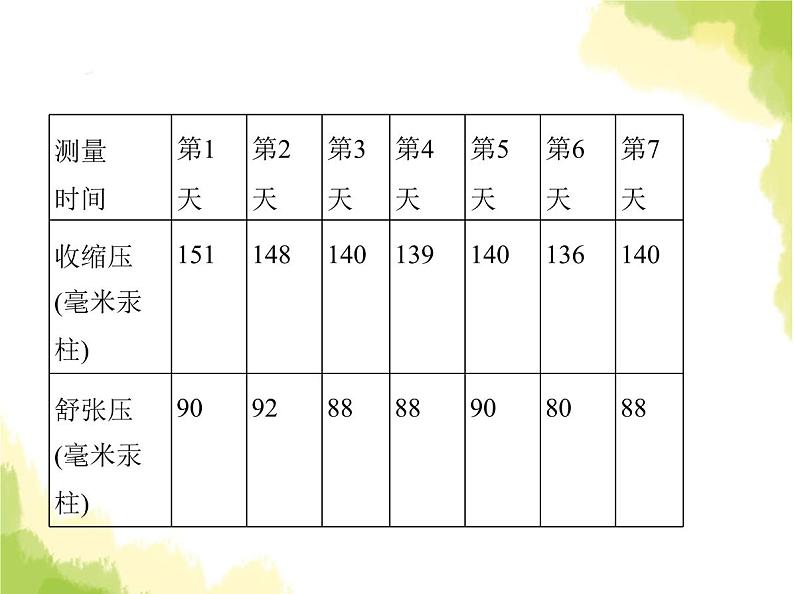
4.(情境题·老年人免费体检)乡村医生李医生在对本村老年 人进行年度免费体检时,发现张奶奶血压偏高,为了准确诊 断,随后7天,李医生每天定时为张奶奶测量血压,测得数据如 下表:
对收缩压、舒张压两组数据分别进行统计分析,其中错误的 是 (　    )A.收缩压的中位数为140B.舒张压的众数为88C.收缩压的平均数为141D.舒张压的方差为 
解析　把7天的收缩压从小到大排列,排在中间的数是140,故 中位数是140,故选项A不符合题意;在7天的舒张压中,88出现的次数最多,所以舒张压的众数为8 8,故选项B不符合题意;收缩压的平均数为 ×(151+148+140+139+140+136+140)=142,故选项C符合题意;舒张压的平均数为 ×(90+92+88+88+90+80+88)=88,舒张压的方差为 ×[2×(90-88)2+(92-88)2+(80-88)2+3×(88-88)2]= ,
故选项D不符合题意.故选C.
5.(2023湖南邵阳中考)如图,在四边形ABCD中,AB∥CD,若 添加一个条件,使四边形ABCD为平行四边形,则下列选项正 确的是 (　    ) A.AD=BC B.∠ABD=∠BDCC.AB=AD D.∠A=∠C
解析　A选项,由AB∥CD,AD=BC不能判定四边形ABCD为 平行四边形,故选项A不符合题意;B选项,∵∠ABD=∠BDC, ∴AB∥CD,∴不能判定四边形ABCD为平行四边形,故选项 B不符合题意;C选项,由AB∥CD,AB=AD不能判定四边形 ABCD为平行四边形,故选项C不符合题意;D选项,∵AB∥ CD,∴∠ABC+∠C=180°,∵∠A=∠C,∴∠ABC+∠A=180°, ∴AD∥BC,又∵AB∥CD,∴四边形ABCD是平行四边形,故 选项D符合题意.故选D.
6.(2024黑龙江绥化望奎期末)如图,在等腰△AOB中,OA= AB,∠OAB=120°,OA在x轴上,将△AOB绕原点O逆时针旋转 120°,得到△A'OB',若OB=2 ,则点A的对应点A'的坐标为 (　    ) 
A.(-1,-1) B.(-1, ) C.(-1,2) D.(-1, )
解析　如图,过B作BC⊥OA于C,延长B'A'交y轴于D, ∵OA=AB,∠OAB=120°,∴∠OBA=∠AOB=30°,∠BAC=60°,∴∠DOB=60°,∠ABC=30°,∵OB=2 ,
∴BC= OB= ,∴OA=AB=2,∵将△AOB绕原点O逆时针旋转120°,得到△A'OB',∴∠B'=3 0°,A'O=OA=2,A'B'=AB=2,OB'=OB=2 ,∠BOB'=120°,∴∠DOB'=60°,∴∠ODB'=90°,∴OD= OB'= ,∴B'D=3,∴A'D=B'D-A'B'=1,∴点A的对应点A'的坐标为(-1, ),故选B.
7.(情境题·数学文化)(2024四川南充期末)《九章算术》是我 国古代重要的数学专著之一,其中记录的一道题译为白话文 是:把一份文件用慢马送到900里外的城市,需要的时间比规 定时间多一天;如果用快马送,所需的时间比规定时间少3天. 已知快马的速度是慢马的2倍,求两匹马的速度.设慢马的速 度为x里/天,则可列方程为 (　    )A. +1= +3 B. -1= -3C. +1= -3 D. -1= +3
解析　慢马的速度为x里/天,则快马的速度为2x里/天,根据规 定时间相等可得 -1= +3.故选D.
8.(2023山东济南历下校级期中)如图,平行四边形ABCD的对 角线AC、BD相交于点O,点E是CD的中点,△ABD的周长为3 2 cm,则△DOE的周长是 (　    ) A.16 cm B.12 cmC.8 cm D.4 cm
解析　∵四边形ABCD是平行四边形,∴AB=CD,AD=BC,BO =DO,∴O是BD的中点,又∵E是CD的中点,∴OE是△BCD的 中位线,∴OE= BC.∵OD= BD,DE= DC,∴△DOE的周长= △BCD的周长,∵△BCD的周长=△DAB的周长,∴△DOE的周长= △DAB的周长= ×32=16(cm).故选A.
9.(2023海南中考改编)如图,在▱ABCD中,AB=8,∠ABC=60 °,BE平分∠ABC,交边AD于点E,连接CE,若AE=2ED,则CE的 长为 (　    ) A.6　　　　B.4　　　　C. 　　　　D. 
解析　∵四边形ABCD是平行四边形,∴∠D=∠ABC=60°, CD=AB=8,AD∥BC,∴∠AEB=∠CBE,∵BE平分∠ABC,∴ ∠ABE=∠CBE,∴∠ABE=∠AEB,∴AE=AB=8,∵AE=2ED, ∴2ED=8,∴ED=4,如图,过点E作EF⊥CD于点F, 则∠EFC=∠EFD=90°,
∴∠FED=90°-∠D=90°-60°=30°,∴DF= ED=2,∴EF= = = ,CF=CD-DF=8-2=6,∴CE= = = ,故选C.
10.(2024浙江杭州上城期末)如图,△ABC中,∠BAC=45°,将 △ABC绕点A逆时针旋转α(0°<α<45°)得到△ADE,DE交AC 于点F.当α=30°时,点D恰好落在BC上,则∠AFE= (　    ) A.80°　　　　B.90°　　　　C.85°　　　　D.95°
解析　∵将△ABC绕点A逆时针旋转α(0°<α<45°),得到△ ADE,∴∠BAC=∠DAE,∠BAD=∠CAE=α=30°,AB=AD,∠C =∠E,∴∠B=75°,∴∠C=∠E=60°,∴∠AFE=180°-60°-30°=9 0°,故选B.
11.(整体思想)(2024山东菏泽单县期中)已知 - =3 ,则 = (　    )A.-  B.3C.2 D.-2
解析　∵ - = =3,∴y-x=3xy,∴ = =-2,故选D.
12.如图,四边形ABCD是平行四边形,AE∥BD,AE与CB的延 长线交于点E,连接DE交AB于点F,连接CF,下列结论:①BC=  EC;②四边形AEBD是平行四边形;③若∠ADF=∠BCF,则∠ABC=90°;④若DF=FC,则△DCE是直角三角形.其中正确 的有 (　    ) 
A.4个 B.3个C.2个 D.1个
解析　∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC, AB∥CD,又∵AE∥BD,∴四边形AEBD是平行四边形,故② 正确;∵四边形AEBD是平行四边形,∴AD=EB,∴EB=BC,∵ EC=EB+BC,∴BC= EC,故①正确;③∵AD∥EC,∴∠ADF=∠FEC,∵∠ADF=∠BCF,∴∠FEC=∠BCF,∴FE=FC,又∵ BC=BE,∴FB⊥BC,即∠ABC=90°,故③正确;④∵四边形 AEBD是平行四边形,∴DF=EF,∵DF=FC,∴EF=FC,∵BE= BC,∴∠ABC=90°,∵AB∥CD,∴∠DCE+∠ABC=180°,∴∠ DCE=90°,∴△DCE是直角三角形,故④正确.故选A.
二、填空题(每小题3分,共24分)
13.(新独家原创)若分式 的值为零,则x的值为　    　    .
解析　∵ 的值为0,∴(x-3)(x+5)=0且x2-25≠0,∴x=3.
14.(2024山东淄博高青期末)某公司决定招聘一名职员,一位 应聘者三项素质测试的成绩如下表:
这三项成绩按照如图所示的比例确定综合成绩,则该应聘者 的综合成绩为　　　    分. 
解析　该应聘者的综合成绩为70×35%+80×40%+92×25%=7 9.5(分).故答案为79.5.
15.(跨学科·历史)(2023山西大同平城模拟)风铃,又称铁马,古 称“铎”,常见于中国传统建筑屋檐下(如图1).图2是六角形 风铃的平面示意图,其底部可抽象为正六边形ABCDEF,连接 AC,CF,则∠ACF的度数为　　　    °.
图1 图2
解析　在正六边形ABCDEF中,∠B=∠BAF=∠AFE=180°-  =120°,AB=CB,∴∠BAC=∠ACB=30°,∴∠CAF=∠BAF-∠BAC=120°-30°=90°,易知∠AFC= ∠AFE=60°,∴∠ACF=90°-∠AFC=30°.故答案为30.
16.已知一组数据1,3,2,2,a,b,c的唯一众数为3,平均数为2,则 这组数据的中位数为　　　    .
解析　因为唯一众数为3,所以可设a=3,b=3,则平均数= (1+3+2+2+3+3+c)=2,解得c=0,将这组数据按从小到大的顺序排列:0,1,2,2,3,3,3,位于最中间 的数是2,所以中位数是2.故答案为2.
17.(2024北京海淀期末)如图,四边形ABCD中,AB∥CD,AD ∥BC,且∠BAD、∠ADC的平分线AE、DF分别交BC于 点E、F.若EF=2,AB=5,则AD的长为　　　    . 
解析　∵AD∥BC,∴∠ADF=∠DFC,∵DF平分∠ADC,∴∠ ADF=∠CDF,∴∠DFC=∠CDF,∴CF=CD,同理可得BE=AB, ∵AB∥CD,AD∥BC,∴四边形ABCD是平行四边形,∴AB= CD,AD=BC,∴AB=BE=CF=CD=5,∴BC=BE+CF-EF=5+5-2= 8,∴AD=BC=8.故答案为8.
18.(2022山东济南莱芜期末)在平面直角坐标系中,点A的坐 标为(0,6),点B的坐标为(2,4),△OAB沿x轴向右平移,得到△ EDF,点B的对应点F是直线y= x上的一点,则点A的对应点D的坐标为　　　    . 
解析　连接AD,BF(图略),∵点A的坐标为(0,6),点B的坐标为 (2,4),△OAB沿x轴向右平移,得到△EDF,∴点D的纵坐标是 6,点F的纵坐标是4.又∵点B的对应点F是直线y= x上的一点,∴设点F的横坐标为a,则4= a,解得a=7.∴点F的坐标是(7,4),∴BF=5.根据平移的性质知AD=BF=5,∴点A的对应点D的 坐标为(5,6).
19.如图,l1∥l2∥l3∥l4,相邻两条平行线间的距离为1,A为l1上 一定点,B,D分别为l3,l4上的动点,以AB,AD为边作▱ABCD,则 AC长的最小值为　　　    . 
解析　如图,过点C作CF⊥l3,垂足为点F,交l4于点E,过点A作 AM⊥l3,垂足为点M. ∵l1∥l2∥l3∥l4,CF⊥l3,AM⊥l3,相邻两条平行线间的距离为1,∴CE⊥l4,EF=1,AM=2,∴∠CED=∠AMB=90°,易知CF∥AM,
∴∠ACF=∠CAM,∵四边形ABCD为平行四边形,∴DC=AB,DC∥AB,∴∠ACD=∠CAB,∴∠DCE=∠BAM,∴△DCE≌△BAM(AAS),∴CE=AM=2,∴CF=CE+EF=3,∴当AC⊥l1时,AC有最小值,最小值为3+2=5.
20.(2024新疆伊犁州期末)如图,在平面直角坐标系中,将△ ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在 点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到 △A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转 到△A2B2C2的位置,点A2在x轴上,依次进行下去,…….若点A  ,B(0,2),则点B2 023的坐标为　　　    . 
解析　由图象可知点B2 023在x轴上,∵OA= ,OB=2,∠AOB=90°,∴AB= = = ,∴B1(4,0),B3(10,0),B5(16,0),……,∴OB1=4,B1B3=B3B5=6,∵2 023÷2=1 011……1,1 011×6=6 066,6 066+4=6 070,∴B2 023(6 070,0).
三、解答题(共60分)
21.[答案含评分细则](2024山东临沂费县期末)(8分)分解因 式:(1)-a3+6a2-9a.(2)x2(x-3)+4(3-x).
解析    (1)-a3+6a2-9a=-a(a2-6a+9) 2分=-a(a-3)2. 4分(2)x2(x-3)+4(3-x)=x2(x-3)-4(x-3) 6分=(x-3)(x2-4)=(x-3)(x+2)(x-2). 8分
22.[答案含评分细则](2021山东聊城中考)(8分)(1)解方程: + = .(2)先化简,再求值: ÷ ,其中x=-2.
解析    (1)∵ + = ,∴ + = ,∴2(1-x)+5(1+x)=10, 1分∴2-2x+5+5x=10,∴7+3x=10,∴3x=3,∴x=1, 2分检验:当x=1时,1-x2=0,  3分
故原分式方程无解. 4分(2)原式= ÷ = ·   5分= · = ·  6分=-x(x+1)=-x2-x, 7分当x=-2时,原式=-(-2)2-(-2)=-4+2=-2. 8分
23.[答案含评分细则](6分)如图,在平面直角坐标系中,△ ABC的三个顶点分别为A(-3,5),B(-2,1),C(-1,3).(1)若△ABC经过平移后得到△A1B1C1,点C1的坐标为(4,0),写 出顶点A1,B1的坐标.(2)若△ABC和△A2B2C2关于原点O成中心对称,写出△A2B2C 2各顶点的坐标.(3)若将△ABC绕点O按顺时针方向旋转90°,得到△A3B3C3, 写出△A3B3C3各顶点的坐标.
解析    (1)如图所示,点A1,B1的坐标分别为(2,2),(3,-2). 2分 (2)如图所示,点A2的坐标为(3,-5),点B2的坐标为(2,-1),点C2的 坐标为(1,-3).  4分
(3)如图所示,点A3的坐标为(5,3),点B3的坐标为(1,2),点C3的坐 标为(3,1). 6分
24.[答案含评分细则](情境题·中华优秀传统文化)(8分)中华 优秀传统文化是中华民族的“根”和“魂”,是最深厚的文 化软实力,为了大力弘扬中华优秀传统文化,某校决定开展名 著读书活动,用3 400元购买“四大名著”若干套后,发现这 批图书满足不了学生的阅读需求,图书管理员在购买第二批 时正赶上图书城8折销售该套图书的活动,因此用3 200元购 买的图书套数反而比第一批多3套.(1)求第一批购买的“四大名著”每套的价格.(2)该校共购买“四大名著”多少套?
解析    (1)设第一批购买的“四大名著”每套的价格为x元, 则第二批购买的“四大名著”每套的价格为0.8x元. 1分依题意得 - =3, 2分解得x=200, 3分经检验,x=200是原方程的解,且符合题意. 4分答:第一批购买的“四大名著”每套的价格是200元. 5分(2) =17(套), 6分17+3=20(套),17+20=37(套). 7分
答:该校共购买“四大名著”37套. 8分
25.[答案含评分细则](情境题·海洋知识大科普)(2024山东青 岛期末)(10分)青岛是一座因海而生、向海而兴的城市,海洋 是青岛高质量发展的战略要地,也是青岛最鲜明的特色.为普 及海洋科学知识,探索海洋奥秘,启迪创新思维,激发科学兴 趣,某校组织了海洋知识竞赛.下面是甲、乙两组学生(参赛 人数相等)竞赛成绩的统计图和统计表:甲组竞赛成绩统计表
1.本次竞赛满分为10分.2.得分情况只有7分、8分、9分、10分.
请根据以上信息,解答下列问题:(1)甲组竞赛成绩统计表中a的值为　　　    .(2)补全条形统计图.(3)经计算,乙组的平均分是8.3分,方差是1.51,请求出甲组的 平均分、方差,并从平均分和方差两个角度综合分析哪个小 组的竞赛成绩更好一些.
解析    (1)参赛人数为4÷20%=20,∴a=20-10-0-8=2.故答案为2. 2分(2)乙组成绩为8分的人数为20-8-4-5=3, 3分补全条形统计图如图.
  (5分)(3)甲组的平均分: =8.3(分), 7分方差: ×[10×(7-8.3)2+2×(8-8.3)2+8×(10-8.3)2]=2.01, 9分∵甲乙两组的平均分都是8.3分,乙组的方差是1.51,1.51<2. 01
∴乙组的成绩更稳定,∴乙组的竞赛成绩更好一些. 10分
26.[答案含评分细则](2023浙江温州鹿城校级二模)(10分)如 图,在四边形ABCD中,AD∥BC,AE⊥BC于E,CF⊥AB于F,AE 与CF相交于点G,连接GD,已知∠1=∠2,∠3=∠4.(1)求证:四边形ABCD为平行四边形.(2)若AG=3,DG=5,求四边形ABCD的面积. 
解析    (1)证明:∵CF⊥AB,∴∠AFG=90°, 1分∵∠1=∠2,∠1=∠AGF,∴∠AGF=∠2,∵∠3=∠4, 3分∴∠DCG=∠AFG=90°, 4分∴AB∥DC,∵AD∥BC,∴四边形ABCD为平行四边形. 5分
(2)∵AD∥BC,AE⊥BC,∴AE⊥AD, ∵AG=3,DG=5,∴AD= =4, 6分∵四边形ABCD为平行四边形, ∴BC=AD=4,AB=CD,如图,过点C作CH⊥DG于点H,
 ∴∠AEB=∠DHC=90°,∵∠3=∠4,∴△ABE≌△DCH(AAS),∴BE=CH,AE=DH, 8分∵∠1=∠2,CH⊥DG,CE⊥AE,∴CE=CH,
∴BE=CE=CH= BC=2,在Rt△CGE和Rt△CGH中, ∴Rt△CGE≌Rt△CGH(HL),∴GE=GH, 9分设GE=GH=x,∴DH=DG-GH=5-x,AE=AG+GE=3+x,∵AE=DH,∴5-x=3+x,
∴x=1,∴AE=4,∴四边形ABCD的面积=BC·AE=4×4=16. 10分
27.[答案含评分细则](10分)如图,点E为▱ABCD的边AD上 的一点,连接EB并延长到点F,使BF=BE,连接EC并延长到点 G,使CG=CE,连接FG,H为FG的中点,连接DH,AF.(1)若∠BAE=65°,∠DEC=40°,求∠ECD的度数.(2)求证:四边形AFHD为平行四边形.(3)连接EH,交BC于点O,若OC=OH,求证:EF⊥EG.
解析    (1)∵四边形ABCD是平行四边形,∴∠BCD=∠BAE=65°,AD∥BC, 1分∴∠BCE=∠DEC=40°, 2分∴∠ECD=∠BCD-∠BCE=65°-40°=25°. 3分(2)证明:∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,∵BF=BE,CG=CE, 4分∴BC是△EFG的中位线,
∴BC∥FG,BC= FG, ∴AD∥FH,∵H为FG的中点,∴FH= FG, ∴BC=FH, 5分∴AD=FH,∴四边形AFHD是平行四边形. 6分(3)证明:如图,连接CH,BH, 7分
 ∵CE=CG,FH=HG,∴CH是△EFG的中位线,∴CH= EF,CH∥EF, ∵EB=BF= EF,∴BE=CH,