2024年江苏省苏州市中考数学试题（含详细答案解析）

这是一份2024年江苏省苏州市中考数学试题（含详细答案解析），共29页。试卷主要包含了选择题，填空题，计算题，解答题等内容，欢迎下载使用。

1.用数轴上的点表示下列各数，其中与原点距离最近的是( )
A. −3B. 1C. 2D. 3
2.下列图案中，是轴对称图形的是( )
A. B.
C. D.
3.苏州市统计局公布，2023年苏州市全年实现地区生产总值约为2.47万亿元.被首为“最强地级市”.数据“2470000000000”用科学记数法可表示为( )
A. 2.47×1010B. 247×1010C. 2.47×1012D. 247×1012
4.若a>b−1，则下列结论一定正确的是( )
A. a+1bD. a+1>b
5.如图，AB//CD，若∠1=65∘，∠2=120∘，则∠3的度数为( )
A. 45∘B. 55∘C. 60∘D. 65∘
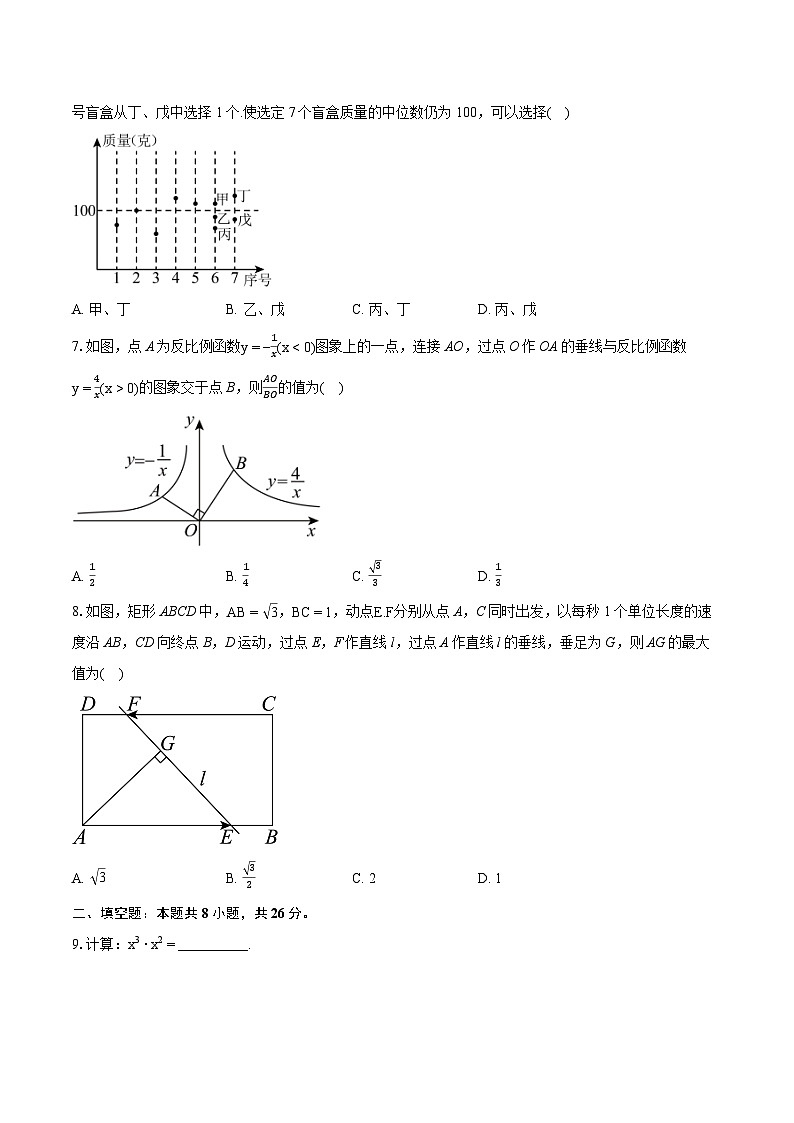
6.某公司拟推出由7个盲盒组成的套装产品，现有10个盲盒可供选择，统计这10个盲盒质量如图所示.序号为1到5号的盲盒已选定，这5个盲盒质量的中位数恰好为100，6号盲盒从甲、乙、丙中选择1个，7号盲盒从丁、戊中选择1个.使选定7个盲盒质量的中位数仍为100，可以选择( )
A. 甲、丁B. 乙、戊C. 丙、丁D. 丙、戊
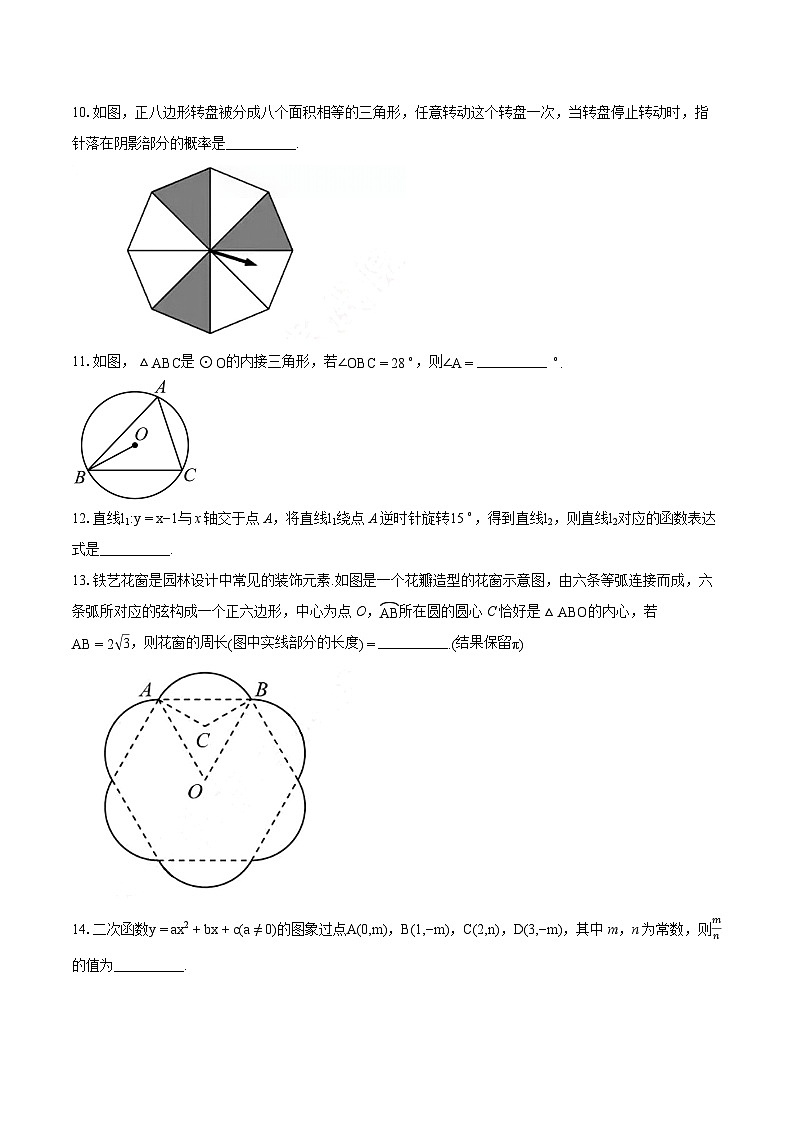
7.如图，点A为反比例函数y=−1x(x<0)图象上的一点，连接AO，过点O作OA的垂线与反比例函数y=4x(x>0)的图象交于点B，则AOBO的值为( )
A. 12B. 14C. 33D. 13
8.如图，矩形ABCD中，AB= 3，BC=1，动点E.F分别从点A，C同时出发，以每秒1个单位长度的速度沿AB，CD向终点B，D运动，过点E，F作直线l，过点A作直线l的垂线，垂足为G，则AG的最大值为( )
A. 3B. 32C. 2D. 1
二、填空题：本题共8小题，共26分。
9.计算：x3⋅x2=__________.
10.如图，正八边形转盘被分成八个面积相等的三角形，任意转动这个转盘一次，当转盘停止转动时，指针落在阴影部分的概率是__________.
11.如图，△ABC是⊙O的内接三角形，若∠OBC=28∘，则∠A=__________ ∘.
12.直线l1:y=x−1与x轴交于点A，将直线l1绕点A逆时针旋转15∘，得到直线l2，则直线l2对应的函数表达式是__________.
13.铁艺花窗是园林设计中常见的装饰元素.如图是一个花瓣造型的花窗示意图，由六条等弧连接而成，六条弧所对应的弦构成一个正六边形，中心为点O，AB所在圆的圆心C恰好是△ABO的内心，若AB=2 3，则花窗的周长(图中实线部分的长度)=__________.(结果保留π)
14.二次函数y=ax2+bx+c(a≠0)的图象过点A(0,m)，B(1,−m)，C(2,n)，D(3,−m)，其中m，n为常数，则mn的值为__________.
15.如图，△ABC中，∠ACB=90∘，CB=5，CA=10，点D，E分别在AC，AB边上，AE= 5AD，连接DE，将△ADE沿DE翻折，得到△FDE，连接CE，CF.若△CEF的面积是△BEC面积的2倍，则AD=__________.
16.若a=b+2，则(b−a)2=__________.
三、计算题：本大题共1小题，共5分。
17.计算：|−4|+(−2)0− 9.
四、解答题：本题共10小题，共75分。解答应写出文字说明，证明过程或演算步骤。
18.(本小题3分)
解方程组：2x+y=7,2x−3y=3.
19.(本小题6分)
先化简，再求值：(x+1x−2+1)÷2x2−xx2−4，其中x=−3.
20.(本小题6分)
如图，△ABC中，AB=AC，分别以B，C为圆心，大于12BC长为半径画弧，两弧交于点D，连接BD，CD，AD，AD与BC交于点E.
(1)求证：△ABD≌△ACD;
(2)若BD=2，∠BDC=120∘，求BC的长.
21.(本小题6分)
一个不透明的盒子里装有4张书签，分别描绘“春”，“夏”，“秋”，“冬”四个季节，书签除图案外都相同，并将4张书签充分搅匀.
(1)若从盒子中任意抽取1张书签，恰好抽到“夏”的概率为__________;
(2)若从盒子中任意抽取2张书签(先抽取1张书签.且这张书签不放回，再抽取1张书签)，求抽取的书签恰好1张为“春”，1张为“秋”的概率.(请用画树状图或列表等方法说明理由)
22.(本小题8分)
某校计划在七年级开展阳光体育锻炼活动，开设以下五个球类项目：A(羽毛球)，B(乒乓球)，C(篮球)，D(排球)，E(足球)，要求每位学生必须参加.且只能选择其中一个项目.为了了解学生对这五个项目的选择情况，学校从七年级全体学生中随机抽取部分学生进行问卷调查，对调查所得到的数据进行整理、描述和分析，部分信息如下：
根据以上信息，解决下列问题：
(1)将图①中的条形统计图补充完整(画图并标注相应数据)；
(2)图②中项目E对应的圆心角的度数为________；
(3)根据抽样调查结果，请估计本校七年级800名学生中选择项目B(乒乓球)的人数.
23.(本小题8分)
图①是某种可调节支撑架，BC为水平固定杆，竖直固定杆AB⊥BC，活动杆AD可绕点A旋转，CD为液压可伸缩支撑杆，已知AB=10cm，BC=20cm，AD=50cm.
(1)如图②，当活动杆AD处于水平状态时，求可伸缩支撑杆CD的长度(结果保留根号);
(2)如图③，当活动杆AD绕点A由水平状态按逆时针方向旋转角度α，且tanα=34(α为锐角)，求此时可伸缩支撑杆CD的长度(结果保留根号).
24.(本小题8分)
如图，△ABC中，AC=BC，∠ACB=90∘，A(−2,0)，C(6,0)，反比例函数y=kx(k≠0,x>0)的图象与AB交于点D(m,4)，与BC交于点E.
(1)求m，k的值；
(2)点P为反比例函数y=kx(k≠0,x>0)图象上一动点(点P在D，E之间运动，不与D，E重合).过点P作PM//AB，交y轴于点M，过点P作PN//x轴，交BC于点N，连接MN，求△PMN面积的最大值，并求出此时点P的坐标.
25.(本小题10分)
如图，△ABC中，AB=4 2，D为AB中点，∠BAC=∠BCD，cs∠ADC= 24，⊙O是△ACD的外接圆．
(1)求BC的长；
(2)求⊙O的半径．
26.(本小题10分)
某条城际铁路线共有A，B，C三个车站，每日上午均有两班次列车从A站驶往C站，其中D1001次列车从A站始发，经停B站后到达C站，G1002次列车从A站始发，直达C站，两个车次的列车在行驶过程中保持各自的行驶速度不变．某校数学学习小组对列车运行情况进行研究，收集到列车运行信息如下表所示．
请根据表格中的信息，解答下列问题：
(1)D1001次列车从A站到B站行驶了______分钟，从B站到C站行驶了______分钟；
(2)记D1001次列车的行驶速度为v1，离A站的路程为d1；G1002次列车的行驶速度为v2，离A站的路程为d2.
①v1v2=______；
②从上午8：00开始计时，时长记为t分钟(如：上午9：15，则t=75)，已知v1=240千米/小时(可换算为4千米/分钟)，在G1002次列车的行驶过程中25≤t≤150，若d1−d2=60，求t的值．
27.(本小题10分)
如图①，二次函数y=x2+bx+c的图象C1与开口向下的二次函数图象C2均过点A(−1,0)，B(3,0).
(1)求图象C1对应的函数表达式；
(2)若图象C2过点C(0,6)，点P位于第一象限，且在图象C2上，直线l过点P且与x轴平行，与图象C2的另一个交点为Q(Q在P左侧)，直线l与图象C1的交点为M，N(N在M左侧).当PQ=MP+QN时，求点P的坐标；
(3)如图②，D，E分别为二次函数图象C1，C2的顶点，连接AD，过点A作AF⊥AD.交图象C2于点F，连接EF，当EF//AD时，求图象C2对应的函数表达式．
答案和解析
1.【答案】B
【解析】【分析】
本题考查了绝对值的定义，一个数的绝对值就是表示这个数的点到原点的距离.到原点距离最远的点，即绝对值最大的点，首先求出各个数的绝对值，即可作出判断.
【解答】
解：∵|−3|=3，|1|=1，|2|=2，|3|=3，
1<2<3，
∴与原点距离最近的是1，
故选B.
2.【答案】A
【解析】【分析】
本题主要考查轴对称图形的概念，掌握轴对称图形的概念是解题的关键.根据如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴进行分析即可.
【解答】
解： A、是轴对称图形，故此选项正确;
B、不是轴对称图形，故此选项错误;
C、不是轴对称图形，故此选项错误;
D、不是轴对称图形，故此选项错误.
故选A.
3.【答案】C
【解析】【分析】
本题考查的是科学记数法-表示较大的数，把一个绝对值大于10的数记成a×10n的形式，其中a是整数数位只有一位的数， n是正整数，这种记数法叫做科学记数法.根据科学记数法-表示较大的数的方法解答.
【解答】
解：2470000000000=2.47×1012，
故选：C.
4.【答案】D
【解析】【分析】
本题主要考查不等式的性质，掌握不等式的性质是解题的关键.不等式的性质：不等式的两边同时加上或减去同一个数或字母，不等号方向不变;不等式的两边同时乘以或除以同一个正数，不等号方向不变;不等式的两边同时乘以或除以同一个负数，不等号方向改变.直接利用不等式的性质逐一判断即可.
【解答】
解：a>b−1，
A、a+1>b，故错误，该选项不合题意;
B、a−1>b−2，故错误，该选项不合题意;
C、无法得出a>b，故错误，该选项不合题意;
D、a+1>b，故正确，该选项符合题意;
故选D.
5.【答案】B
【解析】【分析】
考查平行线的性质求角度，根据题意得出∠BAD=60∘，再由平角即可得出结果，熟练掌握平行线的性质是解题关键.
【解答】
解：∵AB//CD，∠2=120∘，
∴∠2+∠BAD=180∘，
∴∠BAD=60∘，
∵∠1=65∘，
∴∠3=180∘−∠1−∠BAD=55∘
故选B.
6.【答案】C
【解析】【分析】
本题主要考查了用中位数做决策，由图像可知，要使选定7个盲盒质量的中位数仍为100，则需要选择100克以上的一个盲盒和100克以下的盲盒一个，根据选项即可得出正确的答案.
【解答】
解：由图像可知，要使选定7个盲盒质量的中位数仍为100，
则需要从第6号盲盒和第7号盲盒里选择100克以上的一个盲盒和100克以下的盲盒一个，
因此可排除甲、丁，乙、戊，丙、戊；
故选C.
7.【答案】A
【解析】【分析】
本题考查了反比例函数图象上点的坐标特征，反比例函数系数k的几何意义，三角形相似的判定和性质，数形结合是解题的关键.过A作AC⊥x轴于C，过B作BD⊥x轴于D，证明△AOC∽△OBD，利用相似三角形的面积比等于相似比的平方求解即可.
【解答】
解：过A作AC⊥x轴于C，过B作BD⊥x轴于D，
∴S△ACO=12×|−1|=12，S△BDO=12×|4|=2，∠ACO=∠ODB=90∘，
∵OA⊥OB，
∴∠AOC=∠OBD=90∘−∠BOD，
∴△AOC∽△OBD，
∴S△ACOS△BDO=(OAOB)2，即14=(OAOB)2，
∴OAOB=12(负值舍去)，
故选：A.
8.【答案】D
【解析】【分析】
本题主要考查了矩形的性质、动点轨迹、与圆有关的位置关系等知识，根据矩形的性质以及直角三角形斜边中线的性质确定 G的轨迹是本题解题的关键.
连接AC， BD交于点O，取 OA中点H，连接 GH，根据直角三角形斜边中线的性质，可以得出 G的轨迹，从而求出 AG的最大值.
【解答】
解：连接AC，BD交于点O，取OA中点H，连接GH，
如图所示：
∵四边形ABCD是矩形，
∴∠ABC=90∘，OA=OC，AB//CD，
∴在Rt△ABC中，AC= AB2+BC2= ( 3)2+12=2，
∴OA=OC=12AC=1，
∵AB//CD，
∴∠EAO=∠FCO，
在△AOE与△COF中，
AE=CF∠EAO=∠FCOOA=OC
∴△AOE≌△COF(SAS)，
∴∠AOE=∠COF，
∴E， O， F共线，
∵AG⊥EF，H是OB中点，
∴在Rt△AGO中，GH=12AO=12，
∴G的轨迹为以H为圆心，12为半径即AO为直径的圆弧.
∴AG的最大值为AO的长，即AGmax=AO=1.
故选D.
9.【答案】x5
【解析】【分析】
本题考查了同底数幂的乘法，掌握相应的运算法则是解题的关键.
利用同底数幂的乘法解题即可.
【解答】
解：x3⋅x2=x3+2=x5，
故答案为x5.
10.【答案】38
【解析】【分析】
本题考查几何概率的求法：首先根据题意将代数关系用面积表示出来，一般用阴影区域表示所求事件(A)，然后计算阴影区域的面积在总面积中占的比例，这个比例即事件(A)发生的概率.
首先确定在图中阴影区域的面积在整个面积中占的比例，根据这个比例即可求出指针指向阴影区域的概率.
【解答】
解：∵转盘被分成八个面积相等的三角形，其中阴影部分占3份，
∴指针落在阴影区域的概率为38，
故答案为：38.
11.【答案】62
【解析】【分析】
本题考查了圆周角定理，等腰三角形的性质，三角形内角和定理，连接 OC，利用等腰三角形的性质，三角形内角和定理求出∠BOC的度数，然后利用圆周角定理求解即可.
【解答】
解：连接OC，
∵OB=OC，∠OBC=28∘，
∴∠OCB=∠OBC=28∘，
∴∠BOC=180∘−∠OCB−∠OBC=124∘，
∴∠A=12∠BOC=62∘，
故答案为62∘.
12.【答案】y= 3x− 3
【解析】【分析】
本题主要考查一次函数与坐标轴的交点、直线的旋转、解直角三角形以及待定系数法求一次函数解析式，解题的关键是找到旋转后对应的直角边长，即可利用待定系数法求得解析式.
根据题意可求得l1与坐标轴的交点A和点B，可得∠OAB=∠OBA=45∘，结合旋转得到∠OAC=60∘，则∠OCA=30∘，求得OC=OC⋅tan∠OCA，即有点C，利用待定系数法即可求得直线l2的解析式.
【解答】
解：依题意画出旋转前的函数图象l1和旋转后的函数图象l2，如图所示：
设l1与y轴的交点为点B，
令x=0，得y=−1;
令y=0，即x=1，
∴A(1,0)，B(0,−1)，
∴OA=1，OB=1，即∠OAB=∠OBA=45∘
∵直线l1绕点A逆时针旋转15∘，得到直线l2，
∴∠BAC=15∘
∴∠OAC=60∘，
∴OC=OA⋅tan∠OAC= 3OA= 3，则点C(0,− 3)，
设直线l2的解析式为y=kx+b，
则0=k+b− 3=b，
解得k= 3b=− 3，
那么，直线l2的解析式为y= 3x− 3，
故答案为：y= 3x− 3.
13.【答案】8π
【解析】【分析】
考查正多边形与圆，解三角形，求弧长，过点C作CE⊥AB，根据正多边形的性质得出△AOB为等边三角形，再由内心的性质确定∠CAO=∠CAE=∠CBE=30∘，得出∠ACB=120∘，利用余弦得出AC=AEcs30∘=2，再求弧长即可求解，熟练掌握这些基础知识点是解题关键.
【解答】
解：如图所示：过点C作CE⊥AB，
∵六条弧所对应的弦构成一个正六边形，
∴∠AOB=60∘，OA=OB，
∴△AOB为等边三角形，
∵圆心C恰好是△ABO的内心，
∴∠CAO=∠CAE=∠CBE=30∘，
∴∠ACB=120∘，
∵AB=2 3，
∴AE=BE= 3，
∴AC=AEcs30∘=2，
∴AB的长为：120×2×π180=43π，
∴花窗的周长为：43π×6=8π，
故答案为8π.
14.【答案】−35
【解析】【分析】
本题考查了待定系数法求二次函数解析式，把 A、B、D的坐标代入y=ax2+bx+c(a≠0)，求出 a、b、c，然后把 C的坐标代入可得出m、n的关系，即可求解.
【解答】
解：把A(0,m)，B(1,−m)，D(3,−m)代入y=ax2+bx+c(a≠0)，
得c=ma+b+c=−m9a+3b+c=−m，
解得a=23mb=−83mc=m，
∴y=23mx2−83x+m，
把C(2,n)代入y=23mx2−83mx+m，
得n=23m×22−83m×2+m，
∴n=−53m，
∴mn=m−53m=−35，
故答案为：−35.
15.【答案】103
【解析】【分析】
本题考查了相似三角形的判定与性质、折叠性质、等腰直角三角形的判定与性质、全等三角形的判定与性质、三角形的面积公式等知识，是综合性强的填空压轴题，熟练掌握相关知识的联系与运用是解答的关键.
设AD=x，AE= 5x，根据折叠性质得DF=AD=x，∠ADE=∠FDE，过E作EH⊥AC于H，设EF与AC相交于M，证明△AHE∽△ACB得到EHBC=AHAC=AEAB，进而得到EH=x，AH=2x，证明Rt△EHD是等腰直角三角形得到∠HDE=∠HED=45∘，可得∠FDM=90∘，证明△FDM≌△EHM(AAS)得到DM=MH=12x，则CM=AC−AD−DM=10−32x，根据三角形的面积公式结合已知可得(10−32x)x=2(25−5x)，然后解一元二次方程求解x值即可.
【解答】
解：∵AE= 5AD，
∴设AD=x，AE= 5x，
∵△ADE沿DE翻折，得到△FDE，
∴DF=AD=x，∠ADE=∠FDE，
过E作EH⊥AC于H，设EF与AC相交于M，
则∠AHE=∠ACB=90∘，又∠A=∠A，
∴△AHE∽ACB，
∴EHBC=AHAC=AEAB，
∵CB=5，CA=10，AB= AC2+BC2= 102+52=5 5，
∴EH5=AH10= 5x5 5，
∴EH=x，AH= AE2−EH2=2x，则DH=AH−AD=x=EH，
∴Rt△EHD是等腰直角三角形，
∴∠HDE=∠HED=45∘，则∠ADE=∠EDF=135∘，
∴∠FDM=135∘−45∘=90∘，
在△FDM和△EHM中，
∠FDM=∠EHM=90∘∠DMF=∠HMEDF=EH，
∴△FDM≌△EHM(AAS)，
∴DM=MH=12x，CM=AC−AD−DM=10−32x，
∴S△CEF=S△CEM+S△CMF=12CM⋅EH+12CM⋅DF=12(10−32x)⋅x×2=(10−32x)x，
S△BEC=S△ABC−S△AEC=12×10×5−12×10⋅x=25−5x，
∵△CEF的面积是△BEC面积的2倍，
∴(10−32x)x=2(25−5x)，则3x2−40x+100=0，
解得x1=103，x2=10(舍去)，
即AD=103，
故答案为：103.
16.【答案】4
【解析】【分析】
本题考查了求代数式的值，把a=b+2整体代入化简计算即可.
【解答】
解：∵a=b+2，
∴(b−a)2=[b−(b+2)]2=(b−b−2)2=(−2)2=4，
故答案为4.
17.【答案】解：原式=4+1−3=2.
【解析】本题考查了实数的运算，利用绝对值的意义，零指数幂的意义，算术平方根的定义化简计算即可.⋅
18.【答案】解：{2x+y=7①2x−3y=3②
①-②得，4y=4，
解得，y=1.
将y=1代入①得x=3.
∴方程组的解是x=3y=1
【解析】本题考查的是解二元一次方程组，解题的关键是掌握加减消元法求解.
根据加减消元法解二元一次方程组即可.
19.【答案】解：原式=(x+1x−2+x−2x−2)÷x(2x−1)(x+2)(x−2)
=2x−1x−2⋅(x+2)(x−2)x(2x−1)
=x+2x.
当x=−3时，原式=−3+2−3=13.
【解析】本题考查了分式的化简求值，熟练掌握运算法则是解本题的关键.
原式括号中两项通分并利用同分母分式的加法法则计算，同时利用因式分解和除法法则变形，约分得到最简结果，把 x的值代入计算即可求出值.
20.【答案】(1)证明：由作图知：BD=CD.
在△ABD和△ACD中，
∵AB=AC,BD=CD,AD=AD.
∴△ABD≌△ACD(SSS).
(2)解：∵△ABD≌△ACD，∠BDC=120∘，
∴∠BDA=∠CDA=12∠BDC=60∘.
又∵BD=CD，
∴DA⊥BC，BE=CE.
∵BD=2，
∴BE=BD⋅sin∠BDA=2× 32= 3，
∴BC=2BE=2 3.
【解析】本题考查了全等三角形的判定与性质，等腰三角形的性质，解直角三角形等知识，解题的关键是：
(1)直接利用SSS证明△ABD≌△ACD即可;
(2)利用全等三角形的性质可求出∠BDA=∠CDA=60∘，利用三线合一性质得出DA⊥BC，BE=CE，在Rt△BDE中，利用正弦定义求出BE，即可求解.
21.【答案】解：(1)14；
(2)用树状图列出所有等可的结果：
等可能的结果：(春，夏)，(春，秋)，(春，冬)，(夏，春)，(夏，秋)，(夏，冬)，(秋，春)，(秋，夏)，(秋，冬)，(冬，春)，(冬，夏)，(冬，秋)，共12种等可能结果；
∵在12个等可能的结果中，抽取的书签1张为“春”，1张为“秋”出现了2次，
∴P(抽取的书签恰好1张为“春”，1张为“秋”)=16.
【解析】本题考查了利用画树状图或列表的方法求两次事件的概率，解题的关键是：
(1)用标有“夏”书签的张数除以书签的总张数即得结果;
∵有4张书签，分别描绘“春”，“夏”，“秋”，“冬”四个季节，
∴恰好抽到“夏”的概率为14，
故答案为：14;
(2)利用树状图画出所有出现的结果数，再找出1张为“春”，1张为“秋”的结果数，然后利用概率公式计算即可.
22.【答案】解：(1)补全条形统计图如下：
(2)72∘；
(3)800×1860=240(人)，
答：本校七年级800名学生中选择项目B(乒乓球)的人数约为240人.
【解析】解：(1)总人数为9÷15%=60(人)，
D组人数为60−6−18−9−12=15，
补图如下：各项目选择人数条形统计图
(2)360∘×1260=72∘；
故答案为：72∘；
(3)见答案.
本题考查扇形统计图、条形统计图、用样本估计总体，解答本题的关键是明确题意，利用数形结合的思想解答.
(1)利用C组的人数除以所占百分比求出总人数，然后用总人数减去A、B、C、E组的人数，最后补图即可；
(2)用360∘乘以E组所占百分比即可；
(3)用800乘以B组所占百分比即可.
23.【答案】解：(1)如图，过点C作CE⊥AD，垂足为E，

由题意可知，∠B=∠A=90∘，
又∵CE⊥AD，
∴四边形ABCE为矩形.
∵AB=10cm，BC=20cm，
∴AE=20cm，CE=10cm.
∵AD=50cm，
∴ED=30cm.
∴在Rt△CED中，CD= CE2+ED2= 102+302=10 10cm.
即可伸缩支撑杆CD的长度为10 10cm;
(2)过点D作DF⊥BC，交BC的延长线于点F，交AD′于点G.

由题意可知，四边形ABFG为矩形，
∴∠AGD=90∘.
∵在Rt△AGD中，tanα=DGAG=34，
∴DG=34AG.
∴AD= AG2+DG2=54AG，
∵AD=50cm，
∴AG=40cm，DG=30cm.
∴BF=AG=40cm，FG=AB=10cm，
∴CF=20cm，DF=40cm.
∴在Rt△CFD中，CD= CF2+DF2= 202+402=20 5cm.
即可伸缩支撑杆CD的长度为20 5cm.
【解析】本题考查了解直角三角形的应用，解题的关键是：
(1)过点C作CE⊥AD，垂足为 E，判断四边形 ABCE为矩形，可求出 CE， DE，然后在Rt△CED中，根据勾股定理求出CD即可;
(2)过点D作DF⊥BC，交 BC的延长线于点F，交AD′于点G.判断四边形ABFG为矩形，得出∠AGD=90∘.在Rt△AGD中，利用正切定义求出DG=34AG.利用勾股定理求出AD=54AG，由AD=50，可求出BF=AG=40，FG=AB=10，CF=20，DF=40.在Rt△CFD中，根据勾股定理求出 CD即可.
24.【答案】解：(1)∵A(−2,0)，C(6,0)，
∴AC=8.
又∵AC=BC，
∴BC=8.
∵∠ACB=90∘，
∴点B(6,8).
设直线AB的函数表达式为y=ax+b，
将A(−2,0)，B(6,8)代入y=ax+b，得−2a+b=06a+b=8，
解得a=1b=2，
∴直线AB的函数表达式为y=x+2.
将点D(m,4)代入y=x+2，得m=2.
∴D(2,4)
将D(2,4)代入y=kx，得k=8.
(2)延长NP交y轴于点Q，交AB于点L.
∵AC=BC，∠BCA=90∘，
∴∠BAC=45∘.
∵PN//x轴，
∴∠BLN=∠BAC=45∘，∠NQM=90∘.
∵PM//AB，
∴∠MPL=∠BLP=45∘，
∴∠QMP=∠QPM=45∘，
∴QM=QP.
设点P的坐标为(t,8t)，(2∴MQ=PQ=t.
∴S△PMN=12⋅PN⋅MQ=12⋅(6−t)⋅t=−12(t−3)2+92.
∴当t=3时，S△PMN有最大值92，此时P(3,83).
【解析】本题考查了待定系数法求反比例函数解析式，等腰直角三角形的判定和性质，反比例函数图象上点的坐标特征等知识，正确求出相关点的坐标是解题的关键.
(1)先求出B的坐标，然后利用待定系数法求出直线 AB的函数表达式，把 D的坐标代入直线AB的函数表达式求出m，再把D的坐标代入反比例函数表达式求出k即可;
(2)延长NP交y轴于点Q，交 AB于点L.利用等腰直角三角形的判定与性质可得出QM=QP，设点 P的坐标为(t,8t)，(225.【答案】解：(1)∵∠BAC=∠BCD，∠B=∠B，
∴△BAC∽△BCD.
∴BCBD=BABC，即BC2=AB⋅BD
∵AB=4 2，D为AB中点，
∴BD=AD=12AB=2 2，
∴BC2=AB⋅BD=4 2⋅2 2=16
∴BC=4.
(2)过点A作AE⊥CD，垂足为E，连接CO，并延长交⊙O于F，连接AF，
∵在Rt△AED中，cs∠CDA=DEAD= 24.
又∵AD=2 2，
∴DE=1.
∴在Rt△AED中，AE= AD2−DE2= 7.
∵△BAC∽△BCD，
∴ACCD=ABBC= 2.
设CD=x，则AC= 2x，CE=CD−DE=x−1.
∵在Rt△ACE中，AC2=CE2+AE2，
∴ 2x2=x−12+ 72，即x2+2x−8=0，
解得x1=2，x2=−4(舍去).
∴CD=2，AC=2 2.
∵AC⌢=AC⌢，
∴∠AFC=∠ADC.
∵CF为⊙O的直径，
∴∠CAF=90∘.
∴sin∠AFC=ACCF=sin∠CDA=AEAD= 144.
∴CF=8 77，即⊙O的半径为4 77.

【解析】本题考查相似三角形的判定及性质，解直角三角形，圆周角定理．
(1)易证△BAC∽△BCD，得到BCBD=BABC，即可解答；
(2)过点A作AE⊥CD，垂足为E，连接CO，并延长交⊙O于F，连接AF，在Rt△AED中，通过解直角三角形得到DE=1，AE= 7，由△BAC∽△BCD得到ACCD=ABBC= 2.设CD=x，则AC= 2x，CE=x−1，在Rt△ACE中，根据勾股定理构造方程，求得CD=2，AC=2 2，由∠AFC=∠ADC得到sin∠AFC=sin∠ADC，根据正弦的定义即可求解．
26.【答案】解：(1)90，60；
(2)①根据题意得：D1001次列车从A站到C站共需90+60=150分钟，
G1002次列车从A站到C站共需35+60+30=125分钟，
∴150v1=125v2，
∴v1v2=56，
故答案为：56；
②∵v1=4(千米/分钟)，v1v2=56，
∴v2=4.8(千米/分钟).
∵4×90=360，
∴A与B站之间的路程为360.
∵360÷4.8=75，
∴当t=100时，G1002次列车经过B站．
由题意可如，当90≤t≤110时，D1001次列车在B站停车．
∴G1002次列车经过B站时，D1001次列车正在B站停车．
ⅰ.当25≤t<90时，d1>d2，
∴d1−d2=d1−d2，
∴4t−4.8t−25=60，t=75(分钟)；
ⅱ.当90≤t≤100时，d1≥d2，
∴d1−d2=d1−d2，
∴360−4.8t−25=60，t=87.5(分钟)，不合题意，舍去；
ⅲ.当100∴d1−d2=d2−d1，
∴4.8t−25−360=60，t=112.5(分钟)，不合题意，舍去；
ⅳ.当110∴d1−d2=d2−d1，
∴4.8t−25−360+4t−110=60，t=125(分钟).
综上所述，当t=75或125时，d1−d2=60.

【解析】本题考查了一元一次方程的应用，速度、时间、路程的关系，明确题意，合理分类讨论是解题的关键．
(1)直接根据表中数据解答即可；
D1001次列车从A站到B站行驶了90分钟，从B站到C站行驶了60分钟，
故答案为：90，60；
(2)①分别求出D1001次列车、G1002次列车从A站到C站的时间，然后根据路程等于速度乘以时间求解即可；
②先求出v2，A与B站之间的路程，G1002次列车经过B站时，对应t的值，从而得出当90≤t≤110时，D1001次列车在B站停车．G1002次列车经过B站时，D1001次列车正在B站停车，然后分25≤t<90，90≤t≤100，10027.【答案】解：(1)将A(−1,0)，B(3,0)代入y=x2+bx+c，得，
1−b+c=09+3b+c=0，
解得：b=−2c=−3
∴C1对应的函数表达式为：y=x2−2x−3；
(2)设C2对应的函数表达式为y=a(x+1)(x−3)(a<0)，将点C(0,6)代入
得：−3a=6，
解得：a=−2.
∴C2对应的函数表达式为：y=−2(x+1)(x−3)，其对称轴为直线x=−1+32=1.
又∵图象C1的对称轴也为直线x=1，
作直线x=1，交直线l于点H(如答图①)
由二次函数的对称性得，QH=PH，NH=MH
∴PM=NQ.
又∵PQ=MP+QN，而PQ=HP+QH
∴PH=PM.
设PH=t(0将x=t+1代入y=−2(x+1)(x−3)，得yP=−2(t+2)(t−2)，
将x=2t+1代入y=(x+1)(x−3)，得yM=(2t+2)(2t−2).
∵yP=yM，
∴−2(t+2)(t−2)=(2t+2)(2t−2)，
即6t2=12，
解得t1= 2，t2=− 2(舍去).
∴点P的坐标为 2+1,4；
(3)连接DE，交x轴于点G，过点F作FI⊥ED于点I，过点F作FJ⊥x轴于点J.(如答图②)
∵FI⊥ED，FJ⊥x轴，ED⊥x轴，
∴四边形IGJF为矩形，
∴IF=GJ，IG=FJ.
设C2对应的函数表达式为y=a(x+1)(x−3)(a<0)，
∵点D，E分别为二次函数图象C1，C2的顶点，
将x=1分别代入y=x2−2x−3，y=a(x+1)(x−3)(a<0)
得yD=−4,yE=−4a，
∴D(1,−4)，E(1,−4a)，
∴DG=4，AG=2，EG=−4a.
∴在Rt△AGD中，tan ∠ADG=AGDG=24=12.
∵AF⊥AD，
∴∠FAB+∠DAB=90∘.
又∵∠DAG+∠ADG=90∘，
∴∠ADG=∠FAB.
∴tan∠FAB=tan∠ADG=FJAJ=12.
设GJ=m0∴FJ=2+m2，
∴Fm+1,2+m2.
∵EF//AD，
∴∠FEI=∠ADG.
∴tan∠FEI=tan∠ADG=FIEI=12，
∴EI=2m.
又∵EG=EI+IG，
∴2m+2+m2=−4a，
∴a=−2+5m8①
∵点F在C2上，
∴am+1+1m+1−3=m+22，
即am+2m−2=m+22.
∵m+2≠0，
∴am−2=12②
由①，②可得−2+5m8m−2=12.
解得m1=0(舍去)，m2=85，
∴a=−54.
∴C2的函数表达式为y=−54x+1x−3=−54x2+52x+154.

【解析】本题考查了二次函数的图像与性质，待定系数法求函数解析式，二次函数的对称性，矩形的判定与性质，解直角三角形的相关运算，熟练掌握知识点，正确添加辅助线是解决本题的关键．
(1)运用待定系数法求函数解析式即可；
(2)可求C2对应的函数表达式为：y=−2x+1x−3，其对称轴为直线x=1.作直线x=1，交直线l于点H.(如答图①)由二次函数的对称性得，QH=PH，PM=NQ，由PQ=MP+QN，得到PH=PM，设PH=t0(3)连接DE，交x轴于点G，过点F作FI⊥ED于点I，过点F作FJ⊥x轴于点J，(如答图②)，则四边形IGJF为矩形，设C2对应的函数表达式为y=ax+1x−3a<0，可求D1,−4，E1,−4a，则DG=4，AG=2，EG=−4a，而tan∠ADG=AGDG=24=12，则tan∠FAB=tan∠ADG=FJAJ=12.设GJ=m0