第3-4单元易错综合测试卷（月考A卷）四年级数学下册（西师大版）

这是一份第3-4单元易错综合测试卷（月考A卷）四年级数学下册（西师大版），共13页。试卷主要包含了选择题，填空题，判断题，作图题，解答题等内容，欢迎下载使用。

一、选择题（每题1分，共20分）
1．一个三角形的三个内角的度数比是3∶2∶1，这个三角形是（ ）。
A．钝角三角形B．直角三角形C．锐角三角形
2．下列能围成一个三角形的一组小棒是（ ）
A．4cm 6cm 11cm B．5cm 6cm 7cm C．3cm 7cm 10cm
3．一个三角形三个内角的度数比为2：X：7，当X取下列数据中的（ ）时，这个三角形是钝角三角形．
A．7B．8C．9
4．如图所示是小明为爷爷的菜地设计的篱笆，（ ）种方案最稳固．
A．B．C．
5．直角三角形的两锐角和（ ）900，锐角三角形中最大的角（ ）900．
A．大于B．小于C．等于
6．下列线段不能拼成三角形的是（ ）
A．└────┘└──────┘└────┘3厘米 4厘米 3厘米
B．└────┘└──────┘└─┘3厘米 4厘米 1厘米
C．└───────┘└──────┘└─────────┘5厘米 4厘米 6厘米
7．一个等腰三角形的其中两条边是9厘米和2厘米，它的周长是（ ）厘米。
A．18B．13C． 20
8．有一个三角形，从它的顶点起，用一条直线把它分成两个三角形，每个三角形的内角和是（ ）。
A．90°B．180°C．360°
9．将（5，7）点右移3格后的位置用数对表示是（ ）
A．（5，10）B．（2，7）C．（8，7）
10．只看三角形的一个角，（ ）判断出它是什么三角形。
A．能B．不能C．不一定能
二、填空题（每空1分，共16分）
11．迎迎家在学校北偏东30°方向500米处，则学校在迎迎家 偏 ° 米处．
12．张雨晨面向东北，前边是 ，后边是 ，左面是 ，右边是 ．
13．一个三角形的三个内角度数的比是3：4：5，这个三角形最小的一个内角是 度，这是一个 三角形．
14．小明坐在教室的第5列第4行，用（5，4）表示，小红坐在第2列第5行，用数对 来表示，用（6，1）表示的同学坐在第 列第 行．
15．一个三角形三条边都是3厘米，这个三角形既是 三角形，又是 三角形．
16．在一个三角形中，第一个内角的度数是第二个内角度数的3倍；第三个内角的度数是第二个内角度数的二分之一，那么第一个内角是 度．
17．一个三角形两个内角的度数分别为45、55度，则这个三角形为 三角形．
三、判断题（每题2分，共18分）
18．红红家在东偏北30°，距离200m处。( )
19．等腰三角形的一个角是45°，这个三角形一定是直角三角形。（ ）
20．钝角三角形中，最大的角不能小于90°．( )
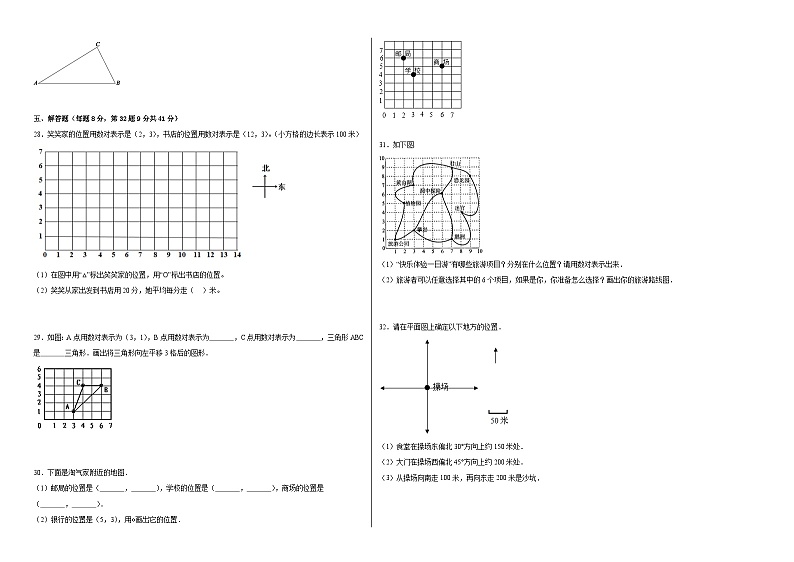
21．如图，如果点X的位置表示为（5,6），则点Y的位置可以表示为（8,7）．
( )
22．任意一个三角形的三个内角和都是180°。( )
23．三角板三个内角的和是180°。( )
24．在图上标出物体的位置时，要先确定距离，再确定方向。( )
25．等腰三角形的一个底角不可能是钝角。( )
26．直角三角形全都是直角 ( )
四、作图题（共5分）
27．一只小蚂蚁想从A点爬到对边BC,沿怎样的路线爬行最短?用笔画下来．
五、解答题（每题8分，第32题9分共41分）
28．笑笑家的位置用数对表示是（2，3），书店的位置用数对表示是（12，3）。（小方格的边长表示100米）
（1）在图中用“△”标出笑笑家的位置，用“O”标出书店的位置。
（2）笑笑从家出发到书店用20分，她平均每分走（ ）米。
29．如图：A点用数对表示为（3，1），B点用数对表示为 ，C点用数对表示为 ，三角形ABC是 三角形．画出将三角形向左平移3格后的图形．
30．下面是淘气家附近的地图．
（1）邮局的位置是（ ， ），学校的位置是（ ， ），商场的位置是（ ， ）．
（2）银行的位置是（5，3），用○画出它的位置．
31．如下图.
（1）“快乐体验一日游”有哪些旅游项目？分别在什么位置？请用数对表示出来．
（2）旅游者可以任意选择其中的6个项目，如果是你，你准备怎么选择？画出你的旅游路线图．
32．请在平面图上确定以下地方的位置．
（1）食堂在操场东偏北30°方向上约150米处．
（2）大门在操场西偏北45°方向上约200米处．
（3）从操场向南走100米，再向东走200米是沙坑．
参考答案：
1．B
【分析】已知三角形内角和是180°，根据按比例分配，求出最大的角，即可解答。
【详解】180°×
＝180°×
＝90°
三角形为直角三角形。
故答案为：B
【点睛】本题考查按比例分配问题；关键明确三角形内角和是180°。
2．B
【详解】试题分析：根据三角形的特性：任意两边之和大于第三边，任意两边之差小于第三边，进行分析即可．
解：A、因为6+4＜11，所以不能围成一个三角形；
B、因为5+6＞7，所以能围成一个三角形；
C、因为3+7=10，所以不能围成一个三角形；
故选B．
【点评】解答此题的关键是根据三角形的特性进行分析、解答即可．
3．D
【详解】试题分析：当三角形中有一个角是钝角时，这个三角形就是钝角三角形．钝角三角形中，两个锐角度数之和小于钝角度数．
解：2+7＜x，即x＞9时，这个三角形是钝角三角形．
故选D．
点评：此题考查了关于三角形的知识：钝角三角形的概念，应明确钝角三角形中，两个锐角度数之和小于钝角度数．
4．C
【详解】试题分析：应用三角形的稳定性和四边形容易变形的特点即可选择正确答案．
解：A、B中为四边形，四边形有容易变形的特点，
C中图形是应用了三角形的稳定性，
所以最不容易变形的是C，
点评：此题考查了三角形的稳定性和四边形容易变形的应用．
5．BC
【详解】试题分析：（1）直角三角形中有一个角是90°，因为三角形内角和是180°，由此即可求出另外两个角的和是180°﹣90°=90°；
（2）锐角三角形的三个角都是锐角，根据锐角的定义可知：小于90°的角是锐角，由此即可选择．
解：（1）180°﹣90°=90°，所以直角三角形的两个锐角和等于90°；
（2）小于90°的角叫锐角，因为锐角三角形的三个角都是锐角，
所以锐角三角形的最大角小于90°；
点评：此题考查直角三角形、锐角三角形的性质和锐角的定义．
6．B
【详解】试题分析：根据三角形的特性：两边之和大于第三边，三角形的两边的差一定小于第三边；进行依次分析、进而得出结论．
解：A、因为3+3＞4，所以三边能拼成三角形；
B、因为3+1=4，所以三边不能拼成三角形；
C、因为5+4＞6，所以三边能拼成三角形；
点评：此题关键是根据三角形的特性进行分析、解答．
7．C
【分析】因为在三角形中任意两边的和大于第三边，所以确定等腰三角形的腰长为9厘米，再把等腰三角形的三条边加起来就是它的周长。
【详解】9＋9＋2
＝18＋2
＝20（厘米）
故答案为：C
【点睛】解答本题的关键是利用在三角形中任意两边的和大于第三边确定等腰三角形的腰长，再利用周长的意义列式解答即可。
8．B
【详解】三角形的内角和是180°。
故答案为：B
9．C
【详解】试题分析：将（5，7）点右移3格，横坐标加上3，纵坐标不变即可．
解：将（5，7）点右移3格后的位置用数对表示是（5+3=8，7），即（8，7）．
故选C．
点评：考查了数对与位置，注意“左减右加，上加下减”，是基础题型．
10．C
【分析】如果这个角大于或等于90°，就可以判定是钝角或者直角三角形；如果小于90°，则不能；进而得出结论。
【详解】由分析知：只看三角形的一个角，不一定能判断出它是什么三角形；
故答案为：C
【点睛】此题考查的是三角形的分类，应根据具体情况进行分析解答。
11．南，西30°，500
【详解】试题分析：根据方向的相对性，北偏东30°方向与南偏西30°相对，据此解答．
解：北偏东30°方向与南偏西30°相对，
所以迎迎家在学校北偏东30°方向500米处，
则学校在迎迎家南偏西30°500米处；
故答案为南，西30°，500．
点评：本题主要考查位置与方向的辨别，注意掌握方向的相对性，北偏东30°方向与南偏西30°相对．
12．东北、西南、西北、东南
【详解】试题分析：面向东北时，前边是东北，后面是西南，左面是西北，右面是东南，可以按这个方位体验一下，据此解答．
解：据分析可知：
张雨晨面向东北，前边是东北，后边是西南，左面是西北，右边是东南．
故答案为东北、西南、西北、东南．
点评：本题主要考查方位的辨别，注意按面向不同的方位体验更好理解．
13．45、锐角．
【详解】试题分析：依据三角形的内角和是180度，利用按比例分配的方法，即可分别求得最小角和最大角的度数，从而可以判定三角形的类别．
解：最小角的度数：180°×=45°，
最大角的度数：180°×=75°，
则这个三角形是锐角三角形；
点评：解答此题的主要依据是：三角形的内角和定理以及判定三角形类别的方法．
14． (2,5) 6 1
15．等边，等腰．
【详解】试题分析：此三角形三条边都是3厘米，即三条边相等，根据三角形的分类，此三角形是等边三角形，等边三角形是等腰三角形的特殊形式，所以此三角形又是等腰三角形．
解：一个三角形三条边都是3厘米，这个三角形既是等边三角形，又是等腰三角形．
点评：此题考查了等边三角形和等腰三角形的关系．
16．120．
【详解】试题分析：其它两个内角都是和第二个内角相比较的，所以可以设第二个内角度数为x，则第一个内角度数为3x，第三个内角度数为x；又任何一个三角形三个内角之和为180°，由此可得方程：x+3x+x=180，解此方程求出第二个内角度数之后，即能求出第一个内角度数．
解：设第二个内角度数为x，由此可得方程：
x+3x+x=180
x=180，
x=40；
第一个内角度数为：40×3=120（度）．
点评：完成本题首先要明确三角形的内角度数和为180度．
17．锐角．
【详解】试题分析：三角形的两个内角的度数已知，依据三角形的内角和是180°，即可求出第三个内角的度数，从而可以判定这个三角形的类别．
解：因为180°﹣45°﹣55°，
=135°﹣55°，
=80°，
所以这个三角形是锐角三角形．
点评：解答此题的主要依据是：三角形的内角和定理以及三角形的分类方法．
18．×
【分析】物体位置对于某一观察点来说，是由一定的方向和距离确定的，只知道方向或距离不能确定物体的位置；
【详解】要说明白；红红家在哪个地方的方向和距离，原题说法错误；
故答案为：×
19．×
【分析】根据等腰三角形的特征，两个底角相等，假如45°的角是底角，再根据三角形的内角和是180°，求出顶角的度数，然后与直角进行比较即可；假如45°的角是顶角，求出底角，进而作出判断。
【详解】假如45°的角是底角，
180°﹣45°﹣45°＝90°；
顶角是90°那么这个三角形是直角三角形。
假如45°的角是顶角，
（180°﹣45°）÷2
＝135°÷2
＝67.5°；
底角是67.5°，那么这个三角形是锐角三角形。
因此，等腰三角形的一个角是45°，这个三角形一定是直角三角形。这种说法是错误的。
故答案为×。
【点睛】此题解答关键是明确：45°的角是底角还是顶角，掌握三角形按照边的长短和按照角的大小分类的标准，
20．√
【详解】根据钝角三角形的定义可知，最大的角大于90°的三角形是钝角三角形；所以答案为对．
21．√
【分析】根据用数对表示点的位置的方法，第一个数字表示列数，第二个数字表示行数，X的位置表示为（5,6），说明X点在第五列，第6行，点Y在点X的右边第三列，说明它比X多3列，即第8列，点Y在点X上方第二行，说明它经X多1行，即第7行，点Y用数对表示是（8,7）．
【详解】如图，
如果点X的位置表示为（5,6），则点Y的位置可以表示为（8,7）．
故答案为√．
【点评】解答此题的关键是根据两点之间的相对位置，及点X所在的列、行确定Y所在列、行．
22．√
【详解】三角形的内角和等于180°。本题结论是正确的。
故答案为：√
23．√
【分析】一副三角板中各个角的度数是：90°、45°、45°；90°、30°、60°；由此判断三角板三个内角的度数和即可。
【详解】三角板是一个三角形，三个内角的和是180°，原题说法正确。
【点睛】本题的关键是掌握三角形的内角和是180°。
24．×
【详解】在图上标出物体的位置时，要先确定方向，再确定距离，原题说法错误。
故答案为：×
25．√
【分析】根据等腰三角形的两个底角相等、三角形的内角和是360°进行举例分析并判断即可。
【详解】大于90°的角是钝角，假设等腰三角形的一个底角是91°，那么这个三角形的两个底角度数为：91°＋91°＝182°，而三角形的内角和才180°，因此等腰三角形的一个底角不可能是钝角。
故答案为：√
【点睛】此题考查的是三角形的内角和，掌握等腰三角形的特点是解答此题的关键。
26．错误
【详解】直角三角形只有一个直角
27．从A点往BC线段做垂线即可，就是最短路线．
【详解】过顶点A作对边的垂线段即可．
28．（1）见详解
（2）50
【分析】（1）数对的第1个数表示位置的列、第2个数表示位置的行，据此标出位置；
（2）根据小方格的边长乘相距的格子数计算出家到书店的距离，再除以行走的时间即可解答。
【详解】（1）
（2）100×10÷20
＝1000÷20
＝50（米）
【点睛】熟练掌握位置与数对的关系是解答本题的关键。
29．（6，4）；（4，4）；钝角 如图
【详解】试题分析：（1）数对表示位置的方法是：第一个数字表示列，第二个数字表示行，据此即可标出点B、C的数对位置；
（2）因为三角形中∠C的度数大于90度，根据钝角三角形的定义可得，这个三角形是钝角三角形；
（3）根据图形平移的方法，把这个三角形的三个顶点分别向左平移3格，再依次连接起来，即可得出平移后的三角形．
解：根据题干分析可得：点B的位置是（6，4）；点C的位置是（4，4），因为三角形中∠C的度数大于90度，根据钝角三角形的定义可得，这个三角形是钝角三角形；画出这个三角形向左平移3格后的三角形如下：
故答案为（6，4）；（4，4）；钝角．
点评：此题考查了数对表示位置的方法以及图形的平移与钝角三角形的定义．
30．（１）2，6；3，4；6，5． （２）如图
【详解】试题分析：（1）数对表示位置的方法是：第一个数字表示列，第二个数字表示行，据此即可标出平面图中各个点的数对位置；
（2）根据银行的位置是（5，3），在图中找出相应的列与行，用○画出它的位置即可．
解：（1）根据数对表示位置的方法可得：邮局的位置是（2，6）；学校的位置是（3，4）；商场的位置是（6，%），
（2）银行的位置如下图：
故答案为2，6；3，4；6，5．
点评：此题主要是灵活利用数对表示位置的方法解决问题．
31．(1)植物园(2，5) 黄山湖(3，7) 君山(7，9) 恐龙园(9，8) 迷宫(8，4) 鹅洲(7，1) 攀岩(3，2) 洞中探险(6，6)
(2)
32．如图
【详解】试题分析：（1）实际距离和比例尺已知，即图上距离1厘米表示实际距离50米，即可求得食堂到操场的图上距离，再据给出的方向（角度），即可标出食堂的位置．
（2）方法一同第一题，先求出大门到操场的图上距离，再据给出的方向（角度），即可标出大门的位置．
（3）先分别求出操场向南100米、再向东200米的图上距离，即可标出沙坑的位置．
解：（1）因为150÷50=3（厘米），
食堂在操场东偏北30°方向上，所以食堂的位置如下图所示；
（2）200÷50=4（厘米）
又因大门在操场的西偏北45°方向，
所以大门的位置如下图所示；
（2）200÷50=4（厘米），
100÷50=2（厘米），
则沙坑的位置如下图所示；
点评：此题主要考查依据物体的方向和距离判定物体位置的方法，以及线段比例尺的意义的灵活应用．