



北京市房山区2023-2024学年高二下学期期末考试数学试题(Word版附解析)
展开第一部分(选择题 共50分)
一、选择题共10小题,每小题5分,共50分.在每小题列出的四个选项中,选出符合题目要求的一项.
1. 已知数列满足,且,则( )
A. B. C. D.
【答案】B
【解析】
【分析】利用等比数列概念及通项可得结果.
【详解】由可得为定值,
又,所以是以为首项,公比的等比数列,
∴=4,
故选:B
2. 函数的图象如图所示,则( )
A.
B.
C.
D.
【答案】C
【解析】
【分析】根据函数的图象结合导数的几何意义判断即可
【详解】根据函数的图象,应用导数的几何意义是函数的切线斜率,
在1处的切线斜率小于在3处的切线斜率,
所以,A,B选项错误;
又因为,所以,D选项错误.
故选:C.
3. 如图 ①、②、③、④ 分别为不同样本数据的散点图,其对应的线性相关系数分别为,则中最大的是( )
A. B.
C. D.
【答案】A
【解析】
【分析】由散点图图形趋势可判断大小关系.
【详解】因③图形比较分散,则;因①②④相较③接近于一条直线附近,则,
又②为下降趋势,则,①比④更接近一条直线,且呈上升趋势,则.
综上,最大
故选:A
4. 设等差数列的前项和为,若,,使最小的的值为( )
A. 4B. 5C. 6D. 4或5
【答案】D
【解析】
【分析】设公差为,依题意得到方程组,求出、,即可求出通项公式,再根据数列的单调性判断即可.
【详解】设公差为,由,,
所以,解得,所以,
令,解得,则数列单调递增,且,
所以当或时取得最小值.
故选:D
5. 要安排5位同学表演文艺节目的顺序,要求甲同学既不能第一个出场,也不能最后一个出场,则不同的安排方法共有( )
A. 种B. 种C. 种D. 种
【答案】A
【解析】
【分析】先将甲同学排列在中间3个位置,再将其余节目全排列即可.
【详解】第一步:先将甲同学排列除第一个、最后一个之外得3个位置,共有种排法,
第二步:将剩余得4个节目全排列,共有种排法,
所以共有种,
故选:
6. 在的展开式中,的系数是( )
A. B. C. D.
【答案】B
【解析】
【分析】写出二项展开式的通项,利用赋值法可得特定项系数.
【详解】由已知可得展开式的通项,
令,解得,
所以,系数为,
故选:B.
7. 某地区气象台统计,夏季里,每天下雨的概率是,刮风的概率为,既刮风又下雨的概率为. 则夏季的某一天里,已知刮风的条件下,也下雨的概率为( )
A. B. C. D.
【答案】D
【解析】
【分析】根据条件概率公式直接可得解.
【详解】设事件为当天下雨,事件为当天刮风,
则,,
则已知刮风的条件下,也下雨的概率,
故选:D.
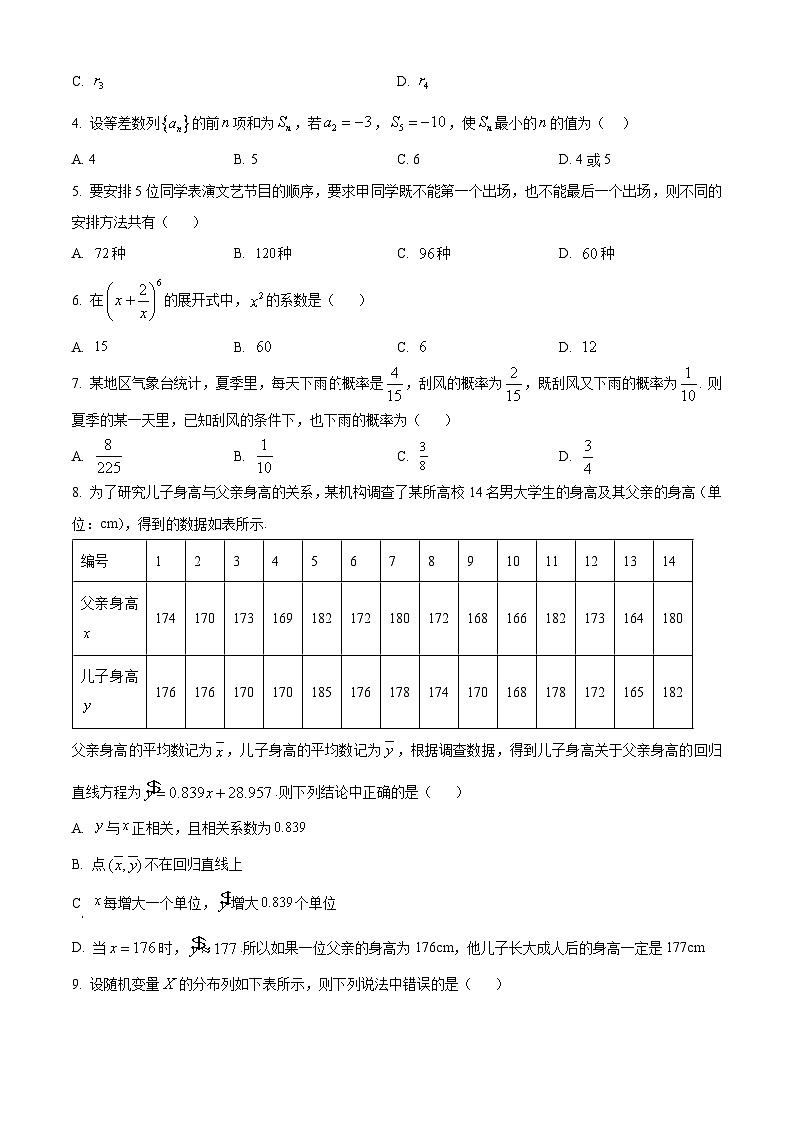
8. 为了研究儿子身高与父亲身高的关系,某机构调查了某所高校14名男大学生的身高及其父亲的身高(单位:cm),得到的数据如表所示.
父亲身高的平均数记为,儿子身高的平均数记为,根据调查数据,得到儿子身高关于父亲身高的回归直线方程为.则下列结论中正确的是( )
A. 与正相关,且相关系数为
B. 点不在回归直线上
C. 每增大一个单位,增大个单位
D. 当时,.所以如果一位父亲的身高为176cm,他儿子长大成人后的身高一定是177cm
【答案】C
【解析】
【分析】由回归方程意义及性质可判断选项正误.
【详解】A选项,因,则与正相关,但相关系数不是,故A错误;
B选项,回归方程过定点,故B错误;
C选项,由回归方程可知每增大一个单位,增大个单位,故C正确;
D选项,回归方程得到的为预测值,不一定满足实际情况,故D错误.
故选:C
9. 设随机变量的分布列如下表所示,则下列说法中错误的是( )
A.
B. 随机变量的数学期望可以等于
C. 当时,
D. 数列的通项公式可以为
【答案】D
【解析】
【分析】根据概率和为可判断A选项;当时,期望为,可判断B选项;根据等比数列求和公式化简可判断C选项;D选项,利用裂项相消法可得的前项和,进而可判断D选项.
【详解】A选项:由已知,则,A选项正确;
B选项:当时,期望为,B选项正确;
C选项:由,则,C选项正确;
D选项:由,则其前项和为,D选项错误;
故选:D.
10. 已知数列:,其中第一项是,接下来的两项是,再接下来的三项是,依此类推. 是数列的前项和,若,则的值可以等于( )
A. B. C. D.
【答案】B
【解析】
【分析】将数列分组,使每组第一项均为1,第一组:,第二组:,第三组:,……,第组:,根据等比例数列前项和公式对选项逐一验证即可.
【详解】将数列分组,使每组第一项均为1,即:
第一组:
第二组:
第三组:
……
第组:
根据等比例数列前项公式,得每组和分别为:,
每组含有的项数分别为.
所以
若,即,
将选项A代入,若,则,即为前5组与第6组的第1个数的和,
此时,无解;
同理若,则,此时,即,符合题意;
同理若,则,此时,无解;
同理若,则,此时,无解;
综上可知,,
故选:
【点睛】关键点点睛:本题关键在于找出数列的规律,对该数列进行分组,利用等比数列前项和公式构造方程,即可求解.
第二部分(非选择题 共100分)
二、填空题共5小题,每小题5分,共25分.
11. 若,则____.
【答案】##
【解析】
【分析】求导代入计算可得结果.
【详解】由可得,
∴,
故答案为:
12. 若,则____;____.
【答案】 ①. 1 ②. -8
【解析】
【分析】利用赋值法,令可得,由通项分别求出可得结果.
【详解】由题意知,令可得,即,
由二项展开式的通项可得,
,即,
,即,
即,
故答案为:
13. 为了提高学生的科学素养,某市定期举办中学生科技知识竞赛.某次科技知识竞赛中,需回答个问题,记分规则是:每答对一题得分,答错一题扣分.从参加这次科技知识竞赛的学生中任意抽取名,设其答对的问题数量为,最后得分为分.当时,的值为____;若,则____.
【答案】 ①. 20 ②. 0.3##
【解析】
【分析】易知当时,答错道题,因此得分为;根据题意得出随机变量与的关系式,再由对立事件概率可求结果.
【详解】由题意知,说明答对道题,答错道题,
又答对得分,答错得分,
所以最后得分,
即当时,;
若,即,可得,
∴,
∴,
故答案为:;
14. 设无穷数列的通项公式为.若是单调递减数列,则的一个取值为____.
【答案】(答案不唯一,即可)
【解析】
【分析】根据数列的函数特性,可得,解不等式可得的取值范围.
【详解】由可得,
又是单调递减数列,可得,
即,
整理得恒成立,
即恒成立,
∴,
又因为,所以,
即取值范围为,
故答案为:(答案不唯一,即可)
15. 已知函数, 给出下列四个结论:
①当时,在定义域上单调递增;
②对任意,存在极值;
③对任意,存在最值;
④设有个零点,则的取值构成的集合是.
其中所有正确结论的序号是____.
【答案】②③④
【解析】
【分析】取值计算判断①;函数的极值点情况判断②,分别求出两段的最大值判断③;分段探讨零点个数判断④即得答案.
【详解】对于①,当时,f(x)=−x2−1,x≤0lnx+2x+1,x>0,,①错误;
对于②,当时,函数在上单调递增,在上单调递减,
函数在处取得极大值,因此对任意,存在极值,②正确;
对于③,当时,,,,
当时,,由,得,由,得,
即函数在上单调递增,在上单调递减,此时,
因此,,③正确;
对于④,当时,函数在上单调递增,,在上无零点,
在上单调递增,,
,在有一个零点,;
当时,,在上单调递增,同理得,
当时,,在上单调递增,,;
当时,,在上有两个零点,
当时,,,
当趋近于正无穷大时,趋近于负无穷大,即在上有两个零点,;
当时,,在上有两个零点,,;
当时,,在上有两个零点,,,
因此的取值构成的集合是,④正确,
所以所有正确结论的序号是②③④.
故答案为:②③④
【点睛】方法点睛:函数零点个数判断方法:(1)直接法:直接求出f(x)=0的解;(2)图象法:作出函数f(x)的图象,观察与x轴公共点个数或者将函数变形为易于作图的两个函数,作出这两个函数的图象,观察它们的公共点个数.
三、解答题共6小题,共75分. 解答应写出文字说明,演算步骤或证明过程.
16. 已知是等差数列,是等比数列,且,,,.
(1)求和的通项公式;
(2)设,求数列的前n项和.
【答案】(1),
(2)
【解析】
【分析】(1)由是等差数列求出,即可求出;
(2)找出,由分组求和得解.
【小问1详解】
设等差数列的公差为d,,
所以
因为,
所以,即等比数列的公比.
所以,.
所以.
【小问2详解】
由(Ⅰ)知,,,
因此
从而数列的前n项和
.
17. 已知函数
(1)求函数的极值点;
(2)若的极小值为,求函数在上的最大值.
【答案】(1)是函数的极小值点;是函数的极大值点.
(2)最大值.
【解析】
【分析】(1)先求导函数再根据导函数正负得出函数的极值;
(2)先根据极小值求出a,再根据极值及边界值求最大值即可.
【小问1详解】
,
令,得或.
,的情况如下:
所以 是函数的极小值点;是函数的极大值点.
【小问2详解】
因为的极小值为,即
解得 ,
又 , .
所以当时,取得最大值.
18. 袋子中有个大小和质地相同的小球,其中个白球,个黑球.从袋中随机摸出一个小球,观察颜色后放回,同时放入一个与其颜色大小相同的小球,然后再从袋中随机摸出一个小球.
(1)求第一次摸到白球的概率;
(2)求第二次摸到白球概率;
(3)求两次摸到的小球颜色不同的概率.
【答案】(1)
(2)
(3).
【解析】
【分析】(1)由古典概型计算可得结果;
(2)由全概率公式计算可得;
(3)根据条件概率公式计算可得.
【小问1详解】
设第一次摸到白球的事件为,则
,即第一次摸到白球的概率为.
【小问2详解】
设第二次摸到白球的事件为,则
,即第二次摸到白球的概率.
【小问3详解】
设两次摸到的小球颜色不同的事件为,则
,即两次摸到的小球颜色不同的概率为.
19. 人工智能(简称)的相关技术首先在互联网开始应用,然后陆续普及到其他行业. 某公司推出的软件主要有四项功能:“视频创作”、“图像修复”、“语言翻译”、“智绘设计”. 为了解某地区大学生对这款软件的使用情况,从该地区随机抽取了名大学生,统计他们最喜爱使用的软件功能(每人只能选一项),统计结果如下:
假设大学生对软件的喜爱倾向互不影响.
(1)从该地区的大学生中随机抽取人,试估计此人最喜爱“视频创作”的概率;
(2)采用分层抽样的方式先从名大学生中随机抽取人,再从这人中随机抽取人,其中最喜爱“视频创作”的人数为,求的分布列和数学期望;
(3)从该地区的大学生中随机抽取人,其中最喜爱“视频创作”的人数为,的方差记作,(2)中的方差记作,比较与的大小.
(结论不要求证明)
【答案】(1)
(2)分布列见解析,
(3)
【解析】
【分析】(1)有古典概型计算可得结果;
(2)利用抽样比可确定6人中有2人最喜欢“视频创作”,求得的所有可能取值及其对应概率可得分布列和期望值(或利用超几何分布计算可得结果);
(3)由(2)可得,由频率估计概率可得地区的大学生中最喜欢“视频创作”的概率为,因此,可得.
【小问1详解】
设从该地区的大学生随机抽取1人,此人选择“视频创作”的事件为A,
则
【小问2详解】
因为抽取的6人中喜欢“视频创作”的人数为,
所以的所有可能取值为,
所以的分布列为:
(或则 )
【小问3详解】
由(2)可得;
由频率估计概率可得地区的大学生中最喜欢“视频创作”的概率为,因此,
可得.
因此.
20. 已知函数.
(1)当时,求曲线在处的切线方程;
(2)当时,求函数的单调区间;
(3)若对于任意的,有,求的取值范围.
【答案】(1)
(2)当时,在和上递减,在上递增;当时,在上递增;当时,在和上递减,在上递增.
(3)
【解析】
【分析】(1)直接计算导数,并利用导数的定义即可;
(2)对分情况判断的正负,即可得到的单调区间;
(3)对和两种情况分类讨论,即可得到的取值范围.
小问1详解】
由,知.
所以当时,有,.
故曲线在处的切线经过,且斜率为,所以其方程为,即.
【小问2详解】
当时,对有,对有,故在和上递减,在上递增;
当时,对有,故在上递增;
当时,对有,对有,故在和上递减,在上递增.
综上,当时,在和上递减,在上递增;
当时,在上递增;
当时,在和上递减,在上递增.
【小问3详解】
我们有.
当时,由于,,故根据(2)的结果知在上递增.
故对任意的,都有,满足条件;
当时,由于,故.
所以原结论对不成立,不满足条件.
综上,的取值范围是.
【点睛】关键点点睛:本题的关键在于对进行恰当的分类讨论,方可得到所求的结果.
21. 若数列满足:对任意,都有,则称是“数列”.
(1)若,,判断,是否是“数列”;
(2)已知是等差数列,,其前项和记为,若是“数列”,且恒成立,求公差的取值范围;
(3)已知是各项均为正整数的等比数列,,记,若是“数列”,不是“数列”,是“数列”,求数列的通项公式.
【答案】(1)数列是“数列”;数列不是“数列”;
(2)
(3)或
【解析】
【分析】(1)直接根据“数列”的定义进行判断即可;
(2)由是等差数列结合是“数列”可知公差,结合等差数列求和公式用含式子表示,进一步结合恒成立即可求解;
(3)由“数列”的每一项()均为正整数,可得且,进一步可得单调递增,故将任意性问题转换为与1比较大小关系可得的范围,结合,或,注意此时我们还要分情况验证是否是“数列”,从而即可得解.
【小问1详解】
对于数列而言,若,则,
所以数列是“数列”;
对于数列而言,若,则,则数列不是“数列”;
【小问2详解】
因为等差数列是“数列”,所以其公差.
因为,所以,
由题意,得对任意的恒成立,
即对任意的恒成立.
当时,恒成立,故;
当时,对任意的恒成立,即
对任意的恒成立,
因为,所以.
所以的取值范围是.
【小问3详解】
设等比数列的公比为,因为,所以,
因为“数列”的每一项均为正整数,由得,
所以且,
因为,
所以,所以单调递增,
所以在数列中,“”为最小项,
而,从而在数列中,“”为最小项.
因为是“数列”,则只需,所以,
因为数列不是“数列”,则,所以,
因为数列的每一项均为正整数,即,所以或,
(1)当时,,则,
令,
又,
所以为递增数列,
又,
所以对于任意的,都有,即,
所以数列为“数列”,符合题意.
(2)同理可知,当时,,则,
令,
又,
所以为递增数列,
又,
所以对于任意的,都有,即,
所以数列为“数列”,符合题意.
综上,或.
【点睛】关键点点睛:第三问关键是首先将恒成立任意性问题转换为与1比较大小得出的值,回过头去检验是否满足题意即可顺利得解.
编号
1
2
3
4
5
6
7
8
9
10
11
12
13
14
父亲身高
174
170
173
169
182
172
180
172
168
166
182
173
164
180
儿子身高
176
176
170
170
185
176
178
174
170
168
178
172
165
182
0
0
递减
a
递增
递减
软件功能
视频创作
图像修复
语言翻译
智绘设计
大学生人数
北京市大兴区2023-2024学年高二上学期期末考试数学试题(Word版附解析): 这是一份北京市大兴区2023-2024学年高二上学期期末考试数学试题(Word版附解析),文件包含北京市大兴区2023-2024学年高二上学期期末检测数学试题Word版含解析docx、北京市大兴区2023-2024学年高二上学期期末检测数学试题Word版无答案docx等2份试卷配套教学资源,其中试卷共24页, 欢迎下载使用。
北京市石景山区2023-2024学年高二下学期期末考试数学试题(Word版附解析): 这是一份北京市石景山区2023-2024学年高二下学期期末考试数学试题(Word版附解析),文件包含北京市石景山区2023-2024学年高二下学期期末数学试卷Word版含解析docx、北京市石景山区2023-2024学年高二下学期期末数学试卷Word版无答案docx等2份试卷配套教学资源,其中试卷共19页, 欢迎下载使用。
北京市房山区2023-2024学年高一下学期学业水平调研(一)数学试题(Word版附解析): 这是一份北京市房山区2023-2024学年高一下学期学业水平调研(一)数学试题(Word版附解析),文件包含北京市房山区2023-2024学年高一下学期学业水平调研一数学试题Word版含解析docx、北京市房山区2023-2024学年高一下学期学业水平调研一数学试题Word版无答案docx等2份试卷配套教学资源,其中试卷共19页, 欢迎下载使用。












