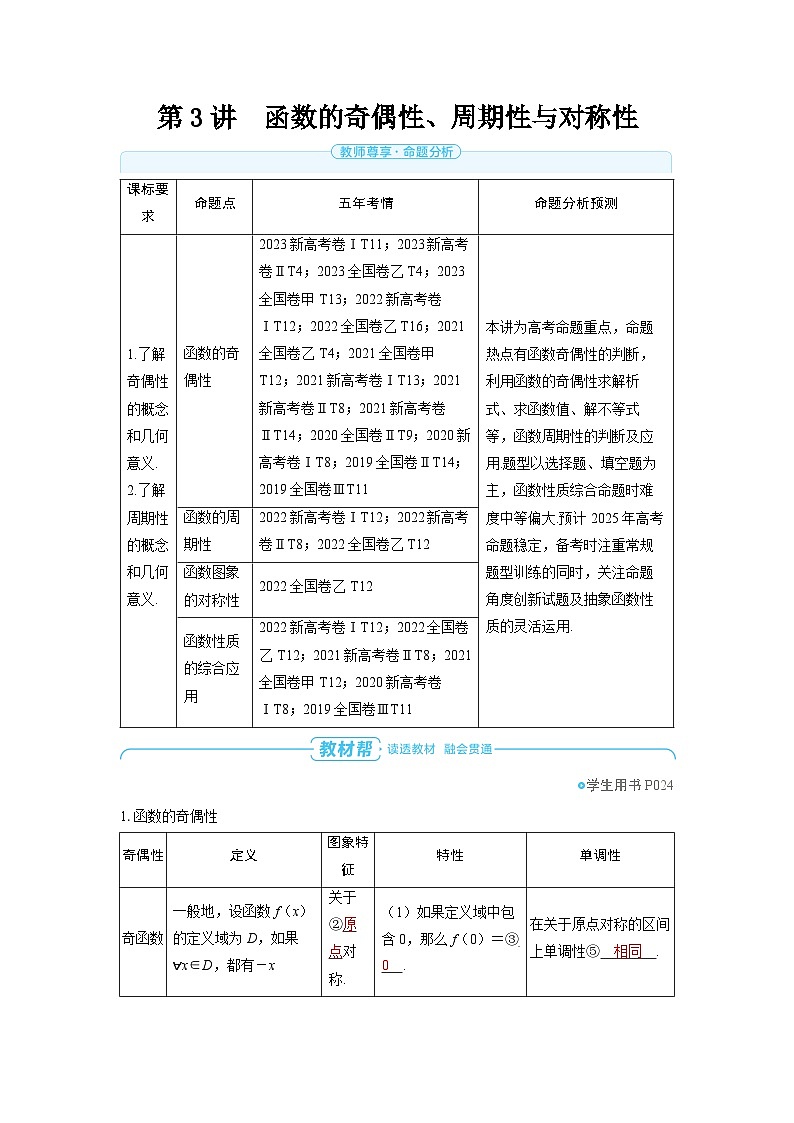


2025年高考数学精品教案第二章 函数 第3讲 函数的奇偶性、周期性与对称性
展开学生用书P024
1.函数的奇偶性
注意 (1)只有函数在x=0处有定义时,f(0)=0才是f(x)为奇函数的必要不充分条件;
(2)既是奇函数又是偶函数的函数只有一种类型,即f(x)=0,x∈D,其中定义域D是关于原点对称的非空数集.
规律总结
1.常见的奇(偶)函数
(1)函数f(x)=ax+a-x为偶函数,函数g(x)=ax-a-x为奇函数;
(2)函数f(x)=ax-a-xax+a-x=a2x-1a2x+1为奇函数,函数g(x)=lgab-xb+x为奇函数;
(3)函数f(x)=lga(x+x2+1)为奇函数,函数g(x)=lga(x2+1-x)也为奇函数.
2.函数奇偶性的拓展结论
(1)若函数y=f(x+a)是偶函数,则f(x+a)=f(-x+a),函数y=f(x)的图象关于直线x=a对称.
(2)若函数y=f(x+b)是奇函数,则f(x+b)+f(-x+b)=0,函数y=f(x)的图象关于点(b,0)中心对称.
2.函数的周期性
(1)周期函数
一般地,设函数f(x)的定义域为D,如果存在一个非零常数T,使得对每一个x∈D都有x+T∈D,且⑨ f(x+T)=f(x) ,那么函数f(x)就叫做周期函数.非零常数T叫做这个函数的周期.
(2)最小正周期
如果在周期函数f(x)的所有周期中存在一个最小的正数,那么这个最小的正数就叫做
f(x)的⑩ 最小 正周期.
注意 并不是所有的周期函数都有最小正周期,如f(x)=5.
常用结论
函数周期性的常用结论
设函数y=f(x),x∈R,a>0,a≠b.
(1)若f(x+a)=-f(x),则2a是函数f(x)的周期;
(2)若f(x+a)=±1f(x),则2a是函数f(x)的周期;
(3)若f(x+a)=f(x+b),则|a-b|是函数f(x)的周期.
3.函数图象的对称性
已知函数f(x)是定义在R上的函数,
(1)若f(a+x)=f(b-x) 恒成立,则y=f(x) 的图象关于直线⑪ x=a+b2 对称.
(2)若f(a+x)+f(b-x)=c,则y=f(x)的图象关于点⑫ (a+b2,c2) 对称.
注意 (1)奇、偶函数的图象平移之后对应的函数不一定有奇偶性,但其图象一定有对称性.(2)注意区分抽象函数的周期性与对称性的表示,周期性的表示中,括号内x的符号相同,对称性的表示中,括号内x的符号相反.
常用结论
函数f(x)图象的对称性与周期的关系
(1)若函数f(x)的图象关于直线x=a与直线x=b对称,则函数f(x)的周期为2|b-a|;
(2)若函数f(x)的图象既关于点(a,0)对称,又关于点(b,0)对称,则函数f(x)的周期为2|b-a|;
(3)若函数f(x)的图象既关于直线x=a对称,又关于点(b,0)对称,则函数f(x)的周期为4|b-a|.
1.已知函数f(x)为奇函数,当x>0时,f(x)=x2+1x,则f(-1)=( A )
A.-2B.0C.1D.2
2.函数f(x)=x+1x图象的对称中心为( B )
A.(0,0)B.(0,1)C.(1,0)D.(1,1)
解析 由题知f(x)=x+1x=1+1x,其图象可由y=1x的图象向上平移一个单位长度得到,又y=1x的图象关于(0,0)对称,所以f(x)=1+1x的图象关于(0,1)对称.
3.[多选]以下函数为偶函数的是( AC )
A.f(x)=x2-1B.f(x)=x3
C.f(x)=x2+cs xD.f(x)=1x+|x|
4.已知函数f(x)为R上的偶函数,且当x<0时,f(x)=x(x-1),则当x>0时,
f(x)= x(x+1) .
5.已知定义在R上的函数f(x)满足f(x)=f(x-2),当x∈[0,2)时,f(x)=x2-4x,则当x∈[4,6)时,f(x)= x2-12x+32 .
解析 设x∈[4,6),则x-4∈[0,2),则f(x-4)=(x-4)2-4(x-4)=x2-12x+32.又f(x)=f(x-2),所以函数f(x)的周期为2,所以f(x-4)=f(x),所以当x∈[4,6)时,f(x)=x2-12x+32.
6.[2024北京市海淀区中国农业大学附属中学模拟]若f(x)=x+a,x<0,bx-1,x>0是奇函数,则a= 1 ,b= 1 .
解析 由f(x)为奇函数,知f(-x)=-f(x),当x>0时,可得-x+a=-bx+1,所以b=1,a=1.
学生用书P026
命题点1 函数的奇偶性
角度1 判断函数的奇偶性
例1 (1)[全国卷Ⅰ]设函数f(x),g(x)的定义域都为R,且 f(x)是奇函数,g(x)是偶函数,则下列结论中正确的是( B )
A. f(x)g(x)是偶函数B. f(x)|g(x)|是奇函数
C.|f(x)|g(x)是奇函数D.|f(x)g(x)|是奇函数
解析 因为f(x)为奇函数,g(x)为偶函数,所以f(x)g(x)为奇函数,f(x)·
|g(x)|为奇函数,|f(x)|g(x)为偶函数,|f(x)g(x)|为偶函数,故选B.
(2)[2021全国卷乙]设函数f(x)=1-x1+x,则下列函数中为奇函数的是( B )
A.f(x-1)-1B.f(x-1)+1
C.f(x+1)-1D.f(x+1)+1
解析 解法一 因为f(x)=1-x1+x,所以f(x-1)=1-(x-1)1+(x-1)=2-xx,f(x+1)=1-(x+1)1+(x+1)=-xx+2.
对于A,F(x)=f(x-1)-1=2-xx-1=2-2xx,定义域关于原点对称,但不满足F(x)=-F(-x);
对于B,G(x)=f(x-1)+1=2-xx+1=2x,定义域关于原点对称,且满足G(x)=
-G(-x);
对于C,f(x+1)-1=-xx+2-1,定义域不关于原点对称;
对于D,f(x+1)+1=-xx+2+1,定义域不关于原点对称.
故选B.
解法二 f(x)=1-x1+x=2-(x+1)1+x=21+x-1,为保证函数变换之后为奇函数,需将函数y=
f(x)的图象向右平移一个单位长度,再向上平移一个单位长度,得到的图象对应的函数为y=f(x-1)+1,故选B.
方法技巧
1.(1)函数定义域关于原点对称是函数有奇偶性的前提条件;(2)若定义域关于原点对称,则判断f(x)与f(-x)是否具有等量关系,具体运算中,可转化为判断f(x)+
f(-x)=0(奇函数)或f(x)-f(-x)=0(偶函数)是否成立.
2.在公共定义域内有:奇函数±奇函数=奇函数,偶函数±偶函数=偶函数,奇函数×奇函数=偶函数,偶函数×偶函数=偶函数,奇函数×偶函数=奇函数.
注意 对于分段函数奇偶性的判断,要分段判断f(-x)=f(x)或f(-x)=-f(x)是否成立,只有当所有区间都满足相同关系时,才能判断该分段函数的奇偶性.
角度2 函数奇偶性的应用
例2 (1)[2023新高考卷Ⅱ]若f(x)=(x+a)·ln2x-12x+1为偶函数,则a=( B )
A.-1B.0C.12D.1
解析 解法一 设g(x)=ln 2x-12x+1,易知g(x)的定义域为(-∞,-12)∪(12,
+∞),且g(-x)=ln -2x-1-2x+1=ln 2x+12x-1=-ln 2x-12x+1=-g(x),所以g(x)为奇函数.若
f(x)=(x+a)ln 2x-12x+1为偶函数,则y=x+a应为奇函数,所以a=0,故选B.
解法二 因为f(x)=(x+a)ln 2x-12x+1为偶函数,f(-1)=(a-1)ln 3,f(1)=(a+1)ln 13=-(a+1)ln 3,所以(a-1)ln 3=-(a+1)ln 3,解得a=0,经检验,满足题意,故选B.
(2)[2024江苏南通模拟]已知定义在R上的函数f(x),g(x)分别是奇函数和偶函数,且f(x)+g(x)=x2-2x,则f(2)+g(1)= -3 .
解析 由f(x)是奇函数,g(x)是偶函数,得f(-x)=-f(x),g(-x)=g(x),∵f(x)+g(x)=x2-2x,∴f(-x)+g(-x)=(-x)2-2(-x)=x2+2x,即
-f(x)+g(x)=x2+2x,则有f(x)=-2x,g(x)=x2,则f(2)+g(1)=-4+1=-3.
方法技巧
函数奇偶性的应用类型及解题策略
(1)求函数解析式或函数值:借助奇偶性转化为求已知区间上的函数解析式或函数值,或利用奇偶性构造关于f(x)的方程(组)求解析式.
(2)求参数值:利用定义域关于原点对称或f(x)±f(-x)=0列方程(组)求解,对于在x=0处有定义的奇函数f(x),可考虑列等式f(0)=0求解.
注意 利用特殊值法求参数时要检验.
训练1 (1)[2024辽宁鞍山一中模拟]下列函数中,既是偶函数又在(0,+∞)上单调递增的是( C )
A.f(x)=xln x
B.f(x)=ln(-x+x2+1)
C.f(x)=ex+e-x
D.f(x)=ex-e-x
解析 对于A,因为f(x)=xln x的定义域为(0,+∞),不关于原点对称,所以f(x)=xln x不是偶函数,故A选项不符合题意;对于B,因为f(x)=ln(-x+x2+1)的定义域为R,关于原点对称,f(x)+f(-x)=ln(-x+x2+1)+ln(x+x2+1)=ln 1=0,所以f(x)=ln(-x+x2+1)是奇函数,故B选项不符合题意;对于C,因为f(x)=ex+e-x的定义域为R,关于原点对称,且f(-x)=e-x+ex=f(x),所以
f(x)=ex+e-x是偶函数.f '(x)=ex-e-x,当x∈(0,+∞)时,有ex>e0=1>e-x,则f '(x)=ex-e-x>0,所以f(x)=ex+e-x在(0,+∞)上单调递增,故C选项符合题意;对于D,因为f(x)=ex-e-x的定义域为R,关于原点对称,但f(-x)=e-x-ex=-(ex-e-x)=-f(x),所以f(x)=ex-e-x是奇函数,故D选项不符合题意.故选C.
(2)[2024江苏省扬州中学模拟]定义在R上的奇函数f(x),当x≥0时,f(x)=2x-a·3-x,当x<0时, f(x)= 3x-2-x .
解析 因为函数f(x)为奇函数,定义域为R,所以f(0)=20-a×30=0,解得a=1.若x<0,则-x>0,所以f(-x)=2-x-3x,又f(x)为奇函数,所以当x<0时,f(x)=-f(-x)=3x-2-x,即当x<0时,f(x)=3x-2-x.
命题点2 函数的周期性
例3 (1)已知f(x+1)是定义在R上且周期为2的函数,当x∈[-1,1)时,f(x)=-2x2+4,-1≤x<0,sin πx,0≤x<1,则 f(3)·f(-103)=( A )
A.3B.-3C.-32D.32
解析 因为f(x+1)是定义在R上且周期为2的函数,
所以f(x)也是周期为2的函数,(解题关键:由f(x+1)的周期得到f(x)的周期)
则f(3)=f(-1)=-2+4=2,f(-103)=f(23)=sin 2π3=32,可得f(3)·f(-103)=2×32=3,故选A.
(2)[2022新高考卷Ⅱ]已知函数f(x)的定义域为R,且f(x+y)+f(x-y)=f(x)·
f(y),f(1)=1,则∑k=122 f(k)=( A )
A.-3B.-2C.0D.1
解析 因为f(1)=1,所以在f(x+y)+f(x-y)=f(x)f(y)中,令y=1,得
f(x+1)+f(x-1)=f(x)f(1),所以f(x+1)+f(x-1)=f(x) ①,所以f(x+2)+f(x)=f(x+1) ②.由①②相加,得f(x+2)+f(x-1)=0,故f(x+3)+f(x)=0,所以f(x+3)=-f(x),所以f(x+6)=-f(x+3)=f(x),所以函数
f(x)的一个周期为6.在f(x+y)+f(x-y)=f(x)f(y)中,令x=1,y=0,得
f(1)+f(1)=f(1)f(0),所以f(0)=2,再令x=0,代入f(x+3)+f(x)=0,得f(3)=-2.令x=1,y=1,得f(2)+f(0)=f(1)f(1),所以f(2)=-1.由
f(x+3)+f(x)=0,得f(1)+f(4)=0,f(2)+f(5)=0,f(3)+f(6)=0,所以f(1)+f(2)+…+f(6)=0,根据函数的周期性知,∑k=122f(k)=f(1)+f(2)+f(3)+f(4)=f(2)+f(3)=-1-2=-3,故选A.
方法技巧
(1)利用函数的周期性可以将局部的函数性质扩展到整体.(2)判断抽象函数的周期一般需要对变量进行赋值.
训练2 (1)[2024广东梅州模拟]已知函数f(x)=ex+1,x≤1,-f(x-1),x>1,则f(2 024-
ln 2)=( A )
A.-e22B.-e2C.e2D.e22
解析 当x>1时,f(x)=-f(x-1),则f(x+2)=-f(x+1)=f(x),所以x>1时,f(x)是周期为2的函数.因为2 024-ln 2=2 022+2-ln 2,且2>2-ln 2>2-ln e=1,所以f(2 024-ln 2)=f(2-ln 2)=-f(1-ln 2)=-e1-ln 2+1=-e2eln2=-e22.故选A.
(2)[2024云南部分名校联考]已知f(x)是定义在R上的偶函数,且f(x)+f(4-x)=0,当0≤x≤2时, f(x)=a·2x+x2,则f(2 024)= -1 .
解析 因为f(x)是定义在R上的偶函数,且f(x)+f(4-x)=0,所以f(x)=-f(4-x)=-f(x-4),f(x-4)=-f(x-8),所以f(x)=f(x-8),故f(x)是以8为周期的函数,则f(2 024)=f(0).令x=2,则f(2)+f(4-2)=2f(2)=8a+8=0,则a=-1,所以f(0)=-20=-1,即f(2 024)=-1.
命题点3 函数图象的对称性
例4 (1)已知函数f(x)(x∈R) 满足f(-x)=2-f(x),若函数y=x+1x 与y=
f(x) 图象的交点为(x1,y1),(x2,y2),…,(xm,ym),则∑i=1m(xi+yi)=( B )
A.0B.mC.2mD.4m
解析 由f(-x)=2-f(x)知f(x)的图象关于点(0,1)对称,而y=x+1x=1+1x的图象也关于点(0,1)对称,因此两个函数图象的交点也关于点(0,1)对称,且成对出现,则x1+xm=x2+xm-1=…=0,y1+ym=y2+ym-1=…=2,所以∑i=1m(xi+yi)=0×m2+2×m2=m.
(2)函数f(x)=(x2-1)(ex-e-x)+x+1在区间[-2,2]上的最大值与最小值分别为M,N,则M+N的值为 2 .
解析 设g(x)=(x2-1)(ex-e-x)+x,则f(x)=g(x)+1.
因为g(-x)=(x2-1)(e-x-ex)-x=-g(x),且g(x)的定义域关于原点对称,所以g(x)是奇函数.
由奇函数图象的对称性知g(x)max+g(x)min=0,
故M+N=[g(x)+1]max+[g(x)+1]min=2+g(x)max+g(x)min=2.
方法技巧
1.解决与函数图象的对称性有关的问题,应结合题设条件的结构特征及对称性的定义,求出函数图象的对称轴或对称中心,进而利用对称性解决求值或参数问题.
2.常用结论:三次函数f(x)=ax3+bx2+cx+d(a≠0)的图象的对称中心为(-b3a,
f(-b3a)).
训练3 (1)[多选]关于函数f(x)=sin x+1sinx,下列结论正确的是( BC )
A.f(x)的图象关于y轴对称
B.f(x)的图象关于原点对称
C.f(x)的图象关于直线x=π2对称
D.f(x)的最小值为2
解析 由题意知f(x)的定义域为{x|x≠kπ,k∈Z},且关于原点对称.又f(-x)=
sin(-x)+1sin(-x)=-(sin x+1sinx)=-f(x),所以函数f(x)为奇函数,其图象关于原点对称,所以A错误,B正确.因为f(π-x)=sin(π-x)+1sin(π-x)=sin x+1sinx=
f(x),所以函数f(x)的图象关于直线x=π2对称,C正确.当sin x<0时,f(x)<0,所以D错误.故选BC.
(2)已知函数f(x)=x3-3x2+x+1+sin(x-1),则函数f(x)在(0,2)上的最大值与最小值的和为 0 .
解析 由三次函数图象的对称性可得,y=x3-3x2+x+1的图象的对称中心为(1,0),因为y=sin(x-1)的图象也关于(1,0)对称,所以函数f(x)在(0,2)上的图象关于(1,0)对称,所以f(x)在(0,2)上的最大值与最小值的和为0.
命题点4 函数性质的综合应用
例5 (1)[2021全国卷甲]设函数f(x)的定义域为R,f(x+1)为奇函数,f(x+2)为偶函数,当x∈[1,2]时,f(x)=ax2+b.若f(0)+f(3)=6,则f(92)=( D )
A.-94B.-32C.74D.52
解析 因为f(x+1)为奇函数,所以函数f(x)的图象关于点(1,0)对称,即有f(x)+f(2-x)=0,令x=1,得f(1)=0,即a+b=0 ①,令x=0,得f(0)=-f(2).因为f(x+2)为偶函数,所以函数f(x)的图象关于直线x=2对称,即有f(x)-f(4-x)=0,令x=1,得f(3)=f(1),所以f(0)+f(3)=-f(2)+f(1)=-4a-b+a+b=-3a=6 ②.根据①②可得a=-2,b=2,所以当x∈[1,2]时,f(x)=-2x2+2.根据函数f(x)的图象关于直线x=2对称,且关于点(1,0)对称,可得函数f(x)的周期为4,所以f(92)=f(12)=-f(32)=2×(32)2-2=52.
(2)[2024平许济洛第一次质检]定义在R上的偶函数f(x)满足f(2-x)+f(x)=0,且f(x)在[-2,0]上单调递增.若a=f(tan5π18),b=f(3),c=f(lg43),则( A )
A.a<b<cB.a<c<b
C.c<b<aD.c<a<b
解析 由f(2-x)+f(x)=0可得f(x)的图象关于点(1,0)中心对称,由f(x)为偶函数可得f(x)的图象关于y轴对称,根据函数周期性结论可得函数f(x)的周期为4,所以f(3)=f(3-4)=f(-1)=f(1),因为0<lg43<1,1=tanπ4<tan5π18<tanπ3=3<2,所以0<lg43<1<tan5π18<2,因为偶函数f(x)在[-2,0]上单调递增,所以函数f(x)在(0,2]上单调递减,所以f(tan5π18)<f(1)=f(3)<f(lg43),即a<b<c.故选A.
方法技巧
1.对于函数单调性与奇偶性的综合问题,常利用奇、偶函数的图象的对称性,以及奇、偶函数在关于原点对称的区间上的单调性求解.
2.对于函数周期性与奇偶性的综合问题,常利用奇偶性及周期性将所求函数值的自变量转换到已知函数解析式的自变量的取值范围内求解.
3.函数的奇偶性、周期性及单调性是函数的三大性质,在高考中常常将它们综合在一起命题,在解题时,往往需要先借助函数的奇偶性和周期性来确定另一区间上的单调性,即实现区间的转换,再利用单调性解决相关问题.
训练4 (1)已知函数f(x)是定义在R上的奇函数,且当x>0时,f(x)=ex+x2+x,则不等式f(2-a)+f(2a-3)>0的解集为( B )
A.(-1,+∞)B.(1,+∞)
C.(-∞,-1)D.(-∞,1)
解析 易知f(x)在(0,+∞)上单调递增,且在(0,+∞)上,f(x)>1.因为f(x)为R上的奇函数,所以f(0)=0,f(x)在(-∞,0)上单调递增,且在(-∞,0)上f(x)<-1,故f(x)在R上单调递增.原不等式可化为f(2-a)>-f(2a-3),即
f(2-a)>f(3-2a),所以2-a>3-2a,故a>1,选B.
(2)[2024湖北部分重点中学联考]已知函数y=f(x)是
R上的奇函数,∀x∈R,都有f(2-x)=f(x)+f(2)成立,则f(1)+f(2)+f(3)+…+f(2 024)= 0 .
解析 因为函数f(x)是R上的奇函数,所以f(0)=0.因为∀x∈R,都有f(2-x)=
f(x)+f(2),所以令x=2,得f(0)=2f(2),得f(2)=0,所以f(2-x)=
f(x),则函数f(x)的图象关于直线x=1对称.因为函数f(x)的图象关于原点对称,所以函数f(x)是以4为周期的周期函数,且函数f(x)的图象关于点(2,0)中心对称,则f(1)+f(3)=0,又f(2)=0,f(4)=f(0)=0,所以f(1)+f(2)+f(3)+f(4)=0,所以f(1)+f(2)+f(3)+…+f(2 024)=506[f(1)+f(2)+f(3)+f(4)]=0.
学生用书P028
抽象函数问题的解题策略
策略1 赋值法
例6 [多选/2023新高考卷Ⅰ]已知函数f(x)的定义域为R,f(xy)=y2f(x)+x2f(y),则( ABC )
A.f(0)=0B.f(1)=0
C.f(x)是偶函数D.x=0为f(x)的极小值点
解析 解法一 令x=y,则有f(x2)=2x2f(x).当x=0时,可得f(0)=0,A正确.当x=1时,可得f(1)=2f(1),所以f(1)=0,B正确.因为f((-x)2)=2(-x)2·
f(-x),即f(x2)=2x2f(-x),所以f(-x)=f(x),所以函数f(x)为偶函数,C正确.因为无法判断函数f(x)的单调性,所以无法确定f(x)的极值点,故D不正确,故选ABC.
解法二 取x=y=0,则f(0)=0,故A正确;取x=y=1,则f(1)=f(1)+f(1),所以f(1)=0,故B正确;取x=y=-1,则f(1)=f(-1)+f(-1),所以
f(-1)=0,取y=-1,则f(-x)=f(x)+x2f(-1),所以f(-x)=f(x),所以函数f(x)为偶函数,故C正确;因为f(0)=0,且函数f(x)为偶函数,所以函数
f(x)的图象关于y轴对称,所以x=0可能为函数f(x)的极小值点,也可能为函数
f(x)的极大值点,也可能不是函数f(x)的极值点,故D不正确.综上,选ABC.
方法技巧
赋值法是指利用已知条件,对变量赋值,从而得出抽象函数在某点处的函数值或抽象函数的性质.
策略2 性质转化法
例7 (1)[2022全国卷乙]已知函数f(x),g(x)的定义域均为R,且f(x)+g(2-x)=5,g(x)-f(x-4)=7.若y=g(x)的图象关于直线x=2对称,g(2)=4,则∑22k=1 f(k)=( D )
A.-21B.-22C.-23D.-24
解析 由y=g(x)的图象关于直线x=2对称,可得g(2+x)=g(2-x).在f(x)+
g(2-x)=5中,用-x替换x,可得f(-x)+g(2+x)=5,可得f(-x)=f(x) ①,所以y=f(x)为偶函数.在g(x)-f(x-4)=7中,用2-x替换x,得g(2-x)=f(-x-2)+7,代入f(x)+g(2-x)=5中,得f(x)+f(-x-2)=-2 ②,所以y=f(x)的图象关于点(-1,-1)中心对称,所以f(1)=f(-1)=-1.由①②可得
f(x)+f(x+2)=-2,所以f(x+2)+f(x+4)=-2,所以f(x+4)=f(x),所以函数f(x)是以4为周期的周期函数.由f(x)+g(2-x)=5可得f(0)+g(2)=5,又g(2)=4,所以可得f(0)=1,又f(x)+f(x+2)=-2,所以f(0)+f(2)=-2,得f(2)=-3,又f(3)=f(-1)=-1,f(4)=f(0)=1,所以∑k=122f(k)=5(f(1)+f(2)+f(3)+f(4))+f(1)+f(2)=-24.故选D.
(2)[多选/2022新高考卷Ⅰ]已知函数f(x)及其导函数f '(x)的定义域均为R,记
g(x)=f '(x).若f(32-2x),g(2+x)均为偶函数,则( BC )
A.f(0)=0B.g(-12)=0
C.f(-1)=f(4)D.g(-1)=g(2)
解析 解法一(转化法) 因为f(32-2x)为偶函数,所以f(32-2x)=f(32+2x),函数f(x)的图象关于直线x=32对称,则f(-1)=f(4),所以C正确;因为g(2+x)为偶函数,所以g(2+x)=g(2-x),函数g(x)的图象关于直线x=2对称,因为g(x)=f'(x),所以函数g(x)的图象关于点(32,0)对称,(二级结论:若函数h(x)为偶函数,则其图象上在关于y轴对称的点处的切线的斜率互为相反数,即其导函数的图象关于原点对称.本题函数f(x)的图象关于直线x=32对称,则其导函数g(x)的图象关于点(32,0)对称)
因为g(x)的定义域为R,所以g(32)=0.由g(x)的图象既关于直线x=2对称,又关于点(32,0)对称,知g(x)的周期T=4×(2-32)=2,所以g(-12)=g(32)=0,
g(-1)=g(1)=-g(2),所以B正确,D错误;不妨取f(x)=1(x∈R),经验证满足题意,则f(0)=1,所以选项A不正确.综上,选BC.
解法二(特例法) 因为f(32-2x),g(2+x)均为偶函数,所以函数f(x)的图象关于直线x=32对称,函数g(x)的图象关于直线x=2对称.取符合题意的一个函数f(x)=1(x∈R),则f(0)=1,排除A;取符合题意的一个函数f(x)=sin πx,则f'(x)=πcs πx,即g(x)=πcs πx,所以g(-1)=πcs(-π)=-π,g(2)=πcs 2π=π,所以g(-1)≠g(2),排除D.又该题为多选题,选BC.
方法技巧
1.思路:利用题设中的条件等式,将其变形为满足函数某些性质的定义表达式,从而利用这些性质转化求解.
2.设函数f(x)及其导函数f '(x)的定义域均为R.
(1)若f(x)的图象关于x=a对称,则f '(x)的图象关于(a,0)对称;
(2)若f(x)的图象关于(a,b)对称,则f '(x)的图象关于x=a对称;
(3)若f(x)是以T为周期的函数,则f '(x)也是以T为周期的函数.
注意 利用函数图象的平移变换解决抽象函数性质问题时,注意在进行图象变换的同时,函数图象的对称轴或者对称中心也进行了相应的变换.
策略3 特殊函数模型法
例8 定义在R上的函数f(x)满足f(x+y)=f(x)+f(y)+2xy(x,y∈R),f(1)=2,则f(-3)=( C )
A.2B.3C.6D.9
解析 解法一 由函数f(x)满足f(x+y)=f(x)+f(y)+2xy(x,y∈R),联想到函数模型f(x)=x2+bx,由f(1)=2,可得b=1,则f(x)=x2+x,所以f(-3)=(-3)2+(-3)=6.
解法二 f(1)=f(1+0)=f(1)+f(0)+2×1×0=f(1)+f(0),得f(0)=0;
f(0)=f(-1+1)=f(-1)+f(1)+2×(-1)×1=f(-1)+2-2=f(-1),得f(-1)=0;f(-2)=f(-1-1)=f(-1)+f(-1)+2×(-1)×(-1)=
2f(-1)+2=2;f(-3)=f(-2-1)=f(-2)+f(-1)+2×(-2)×(-1)=2+0+4=6.故选C.
方法技巧
常用函数模型
注意 应用特殊函数模型法解题时,要注意检验所选模型是否满足已知条件.
训练5 (1)[新高考卷Ⅰ]若定义在R上的奇函数f(x)在(-∞,0)上单调递减,且
f(2)=0,则满足xf(x-1)≥0的x的取值范围是( D )
A.[-1,1]∪[3,+∞)B.[-3,-1]∪[0,1]
C.[-1,0]∪[1,+∞)D.[-1,0]∪[1,3]
解析 由题意知f(x)在(-∞,0),(0,+∞)上单调递减,且f(-2)=f(2)=
f(0)=0.当x>0时,令f(x-1)≥0,得0≤x-1≤2,∴1≤x≤3;当x<0时,令
f(x-1)≤0,得-2≤x-1≤0,∴-1≤x≤1,又x<0,∴-1≤x<0;当x=0时,显然符合题意.综上,原不等式的解集为[-1,0]∪[1,3],故选D.
(2)[多选/2024安徽省阜阳市模拟]已知函数f(x)的定义域为R,对任意实数x,y满足f(x-y)=f(x)-f(y)+1,且f(1)=0,当x>0时,f(x)<1.则下列选项正确的是( ACD )
A.f(0)=1B.f(2)=-2
C.f(x)-1为奇函数D.f(x)为R上的减函数
解析 解法一 设f(x)=kx+1,因为f(1)=0,所以k=-1,所以f(x)=-x+1,满足x>0时,f(x)<1,则易得A,C,D均正确,故选ACD.
解法二 对于A,取x=y=0,则f(0)=f(0)-f(0)+1,故f(0)=1,A正确;
对于B,取x=0,y=1,则f(-1)=f(0)-f(1)+1=2,取x=1,y=-1,则
f(2)=f(1)-f(-1)+1=-1,B错误﹔
对于C,取x=0,则f(-y)=f(0)-f(y)+1=2-f(y),f(-y)-1=-[f(y)-1],则f(y)-1为奇函数,所以f(x)-1为奇函数,C正确;
对于D,当x1>x2时,x1-x2>0,f(x1-x2)<1,则f(x1)-f(x2)=f(x1-x2)-1<0,故f(x)是R上的减函数,D正确,故选ACD.
(3)已知函数f(x)满足f(1)=14,且4f(x)f(y)=f(x+y)+f(x-y)(x,y∈R),则f(2 024)= -14 .
解析 解法一 令y=1,得4f(x)f(1)=f(x+1)+f(x-1),即f(x+1)=f(x)-f(x-1),f(x+2)=f(x+1)-f(x)=-f(x-1),即f(x+3)=-f(x),所以函数f(x)的周期为6,则f(2 024)=f(2).令x=1,y=0,得f(0)=12,由f(x+1)=f(x)-f(x-1),可得f(2)=f(1)-f(0)=-14,所以f(2 024)=-14.
解法二 因为f(x+y)+f(x-y)=4f(x)f(y),x,y∈R,联想到余弦函数模型
cs(x+y)+cs(x-y)=2cs xcs y,两边同除以2,得12cs(x+y)+12cs(x-y)=cs xcs y=4·12cs x12cs y,故猜想f(x)=12cs(ωx),又f(1)=14,则f(1)=12cs ω=14,当ω∈(0,π)时,可得ω=π3,即f(x)=12cs(π3x),故f(x)的周期为T=6,所以f(2 024)=f(2)=12cs 2π3=-14.
1.[命题点1角度2/全国卷Ⅱ]设f(x)为奇函数,且当x≥0时,f(x)=ex-1,则当x<0时,f(x)= ( D )
A.e-x-1B.e-x+1
C.-e-x-1D.-e-x+1
解析 依题意得,当x<0时,f(x)=-f(-x)=-(e-x-1)=-e-x+1,故选D.
2.[命题点1角度2/2023全国卷乙]已知f(x)=xexeax-1是偶函数,则a=( D )
A.-2B.-1C.1D.2
解析 解法一 f(x)的定义域为{x|x≠0},因为f(x)是偶函数,所以f(x)=
f(-x),即xexeax-1=-xe-xe-ax-1,即e(1-a)x-ex=-e(a-1)x+e-x,即e(1-a)x+e(a-1)x=ex+
e-x,所以a-1=±1,解得a=0(舍去)或a=2,故选D.
解法二 f(x)=xexeax-1=xe(a-1)x-e-x,f(x)是偶函数,又y=x是奇函数,所以y=
e(a-1)x-e-x是奇函数,故a-1=1,即a=2,故选D.
3.[命题点2,3/多选/2024江苏省兴化市名校联考]已知函数f(x)为R上的奇函数,
g(x)=f(x+1)为偶函数,下列说法正确的有( ABD )
A.f(x)图象关于直线x=-1对称
B.g(2 023)=0
C.g(x)的周期为2
D.对任意x∈R都有f(2-x)=f(x)
解析 因为函数f(x)为R上的奇函数,所以函数f(x)的图象关于点(0,0)中心对称,因为g(x)=f(x+1)为偶函数,所以f(-x+1)=f(x+1),即函数f(x)的图象关于x=1对称,所以f(-x+1)=-f(-x-1),所以f(x-1)=f(-x-1),所以函数f(x)的图象关于x=-1对称,故A正确;
由f(-x+1)=f(x+1)可得f(2-x)=f(x),故D正确;
由f(2-x)=f(x)可得f(2+x)=f(-x)=-f(x),所以f(4+x)=f(x),即函数f(x)的周期为4,故C错误;
因为f(x)的周期为4,所以g(2 023)=f(2 024)=f(0)=0,故B正确.
故选ABD.
4.[命题点3/2023大同学情调研]函数f(x)=6ex+1+mx|x|+1在[-5,5]上的最大值为M,最小值为N,则M+N=( C )
A.3B.4
C.6D.与m的值有关
解析 由题意可知,f(x)=6ex+1+mx|x|+1=3-3(ex-1)ex+1+mx|x|+1,设g(x)=-3(ex-1)ex+1+mx|x|+1,则g(x)的定义域为(-∞,+∞),g(-x)=-3(e-x-1)e-x+1+m(-x)|-x|+1=
-[-3(ex-1)ex+1+mx|x|+1]=-g(x),所以g(x)为奇函数,所以当x∈[-5,5]时,
g(x)max+g(x)min=0,所以当x∈[-5,5]时,f(x)max+f(x)min=M+N=g(x)max+3+g(x)min+3=6,故选C.
5.[思维帮角度1,2/2021新高考卷Ⅱ]设函数f(x)的定义域为R,且f(x+2)为偶函数,f(2x+1)为奇函数,则( B )
A.f(-12)=0B.f(-1)=0
C.f(2)=0D.f(4)=0
解析 因为函数f(2x+1)是奇函数,所以f(-2x+1)=-f(2x+1),所以f(1)=0,f(-1)=-f(3).因为函数f(x+2)是偶函数,所以f(x+2)=f(-x+2),所以f(3)=f(1),所以f(-1)=-f(1)=0.故选B.
6.[思维帮角度2/多选/2023四省联考]已知f(x)是定义在R上的偶函数,g(x)是定义在R上的奇函数,且f(x),g(x)在(-∞,0]上均单调递减,则( BD )
A.f(f(1))<f(f(2))B.f(g(1))<f(g(2))
C.g(f(1))<g(f(2))D.g(g(1))<g(g(2))
解析 因为f(x)与g(x)分别是定义在R上的偶函数与奇函数,且两函数在(-∞,0]上均单调递减,所以f(x)在[0,+∞)上单调递增,g(x)在[0,+∞)上单调递减,即g(x)在R上单调递减,所以f(1)<f(2),g(2)<g(1)<g(0)=0,(提示:定义在R上的奇函数的图象必过原点)
所以f(g(1))<f(g(2)),g(f(1))>g(f(2)),g(g(1))<
g(g(2)),故B,D正确,C不正确.
若f(1)<f(2)<0,则f(f(1))>f(f(2)),故A不正确.综上所述,选BD.
学生用书·练习帮P266
1.[2024黑龙江省鸡西市第一中学模拟]下列函数中,是奇函数且在定义域内单调递减的是( C )
A.f(x)=tan(-x)B.f(x)=2-x
C.f(x)=e-x-exD.f(x)=2x
解析 f(x)=tan(-x)=-tan x的定义域是{x|x≠kπ+π2,k∈Z},f(x)是奇函数,在定义域上不具有单调性,故A错误;
f(x)=2-x=(12)x既不是奇函数也不是偶函数,在R上单调递减,故B错误;f(x)=
e-x-ex的定义域为R,∵f(-x)=ex-e-x=-f(x),∴f(x)是奇函数,∵y=e-x,y=-ex均为R上的减函数,∴f(x)在R上单调递减,故C正确;f(x)=2x的定义域为{x|x≠0},f(x)是奇函数,在定义域上不具有单调性,故D错误.故选C.
2.若定义在R上的偶函数f(x)和奇函数g(x)满足f(x)+g(x)=ex ,则g(x)=( D )
A.ex-e-x B.12(ex+e-x)
C.12(e-x-ex) D.12(ex-e-x)
解析 因为f(x)+g(x)=ex ,f(x)为偶函数,g(x)为奇函数,所以f(-x)+
g(-x)=f(x)-g(x)=e-x ,所以g(x)=12(ex-e-x) .故选D.
3.已知函数f(x)=x2+2x,x≥0,x2-2x,x<0, 若f(-a)+f(a)≤2f(1),则实数a的取值范围是( C )
A.[-1,0) B.[0,1] C.[-1,1] D.[-2,2]
解析 若x<0,则-x>0,f(-x)=x2-2x=f(x),若x>0,则-x<0,f(-x)=x2+2x=f(x),故函数f(x)为偶函数,且当x≥0时,函数f(x)单调递增,由f(-a)+f(a)≤2f(1),得2f(a)≤2f(1),即f(a)≤f(1),所以|a|≤1,所以
-1≤a≤1.故选C.
4.[2024青岛市检测]若函数f(x)=cs x·lg(x2+m-x)为奇函数,则m=( C )
A.-1B.0C.1D.±1
解析 解法一 因为函数f(x)=cs x·lg(x2+m-x)为奇函数,又y=cs x为偶函数,所以g(x)=lg(x2+m-x)为奇函数,则g(x)+g(-x)=0,即lg(x2+m-x)+lg(x2+m+x)=0,即lg[(x2+m-x)(x2+m+x)]=lg(x2+m-x2)=lg m=0,解得m=1,故选C.
解法二 因为函数f(x)=cs x·lg(x2+m-x)为奇函数,又y=cs x为偶函数,所以g(x)=lg(x2+m-x)为奇函数,所以g(0)=0,即lgm=0,解得m=1.经检验,符合题意.故选C.
5.[2024安徽月考]已知函数f(x)=2sin x+x+2,x∈[-2π,2π],f(x)的最大值为M,最小值为m,则M+m=( A )
A.4B.4π-333C.4π+333D.2π+3-1
解析 因为y=2sin x+x的图象关于原点对称,所以f(x)=2sin x+x+2的图象关于点(0,2)对称,所以f(x)在[-2π,2π]上的最大值与最小值的和M+m=4.故选A.
6.[2023南京市、盐城市一模]若函数f(x)=x3+bx2+cx+d满足f(1-x)+f(1+x)=0对一切实数x恒成立,则不等式f '(2x+3)<f '(x-1)的解集为( C )
A.(0,+∞)
B.(-∞,-4)
C.(-4,0)
D.(-∞,-4)∪(0,+∞)
解析 由f(1-x)+f(1+x)=0可知,函数f(x)的图象关于点(1,0)中心对称.
解法一 易得f '(x)=3x2+2bx+c的图象的对称轴为直线x=1,所以函数f '(x)在
(-∞,1)上单调递减,在(1,+∞)上单调递增,则由f '(2x+3)<f '(x-1),得|2x+3-1|<|x-1-1|,解得-4<x<0,故选C.
解法二 函数f(x)=ax3+bx2+cx+d的图象的对称中心为点(-b3a,f(-b3a)),由
-b3a=1,a=1,得b=-3,所以f '(x)=3x2-6x+c,由f '(2x+3)<f '(x-1),得
3(2x+3)2-6(2x+3)+c﹤3(x-1)2-6(x-1)+c,解得-4<x<0,故选C.
7.[2024福州市一检]已知定义域为R的函数f(x)同时具有下列三个性质,则f(x)= -x(答案不唯一) .(写出一个满足条件的函数即可)
①f(x+y)=f(x)+f(y);②f(x)是奇函数;③当x+y>0时,f(x)+f(y)<0.
解析 因为f(x)是奇函数,且当x+y>0时,f(x)+f(y)<0,即x>-y时,f(x)<-f(y)=f(-y),所以f(x)是单调递减函数,再考虑到f(x+y)=f(x)+
f(y),所以f(x)=kx(k<0)都符合题意.
8.已知f(x)为R上的奇函数,当x>0时,f(x)=-2x2+3x+1,则f(x)的解析式为
f(x)= -2x2+3x+1,x>0,0,x=0,2x2+3x-1,x<0 .
解析 当x<0时,-x>0,则f(-x)=-2(-x)2+3(-x)+1=-2x2-3x+1.
由于f(x)是R上的奇函数,故f(x)=-f(-x),所以当x<0时,f(x)=2x2+3x-1.因为f(x)为R上的奇函数,所以f(0)=0.
综上,f(x)的解析式为f(x)=-2x2+3x+1,x>0,0,x=0,2x2+3x-1,x<0.
9. [2024安徽六校联考]已知函数f(x)=ln(x2+1+x)-2ex+1,则不等式f(x)+
f(2x-1)>-2的解集是( A )
A.(13,+∞)B.(1,+∞)
C.(-∞,13)D.(-∞,1)
解析 因为x2+1>|x|≥-x,所以x2+1+x>0在R上恒成立,所以函数f(x)的定义域为R,f(x)=ln(x2+1+x)+(ex-1)-(ex+1)ex+1=ln(x2+1+x)+ex-1ex+1-1,令h(x)=f(x)+1=ln(x2+1+x)+ex-1ex+1,则h(x)+h(-x)=[ln(x2+1+x)+ex-1ex+1]+[ln(x2+1-x)+e-x-1e-x+1]=ln(x2+1+x)+ln(x2+1-x)+ex-1ex+1+1-ex1+ex=ln 1+0=0,所以h(x)是奇函数.
设g(x)=ln(x2+1+x),则g(x)为奇函数.当x≥0时,y=x2+1,y=x均单调递增,则y=x2+1+x在[0,+∞)上单调递增.所以g(x)=ln(x2+1+x)在[0,+∞)上单调递增.
又g(x)为奇函数且g(0)=0,所以g(x)在R上单调递增.又y=ex+1在R上单调递增,所以y=2ex+1在R上单调递减,所以y=-2ex+1在R上单调递增,所以h(x)=g(x)-2ex+1+1在R上单调递增.
不等式f(x)+f(2x-1)>-2,即f(x)+1>-[f(2x-1)+1],也即h(x)>-
h(2x-1)=h(1-2x),所以x>1-2x,解得x>13.故选A.
10.[2024黄冈模拟]已知函数f(x)及其导函数f '(x)的定义域均为R,记g(x)=
f '(x+1),且f(2+x)-f(2-x)=4x,g(3+x)为偶函数,则g'(7)+g(17)=( C )
A.0B.1C.2D.3
解析 因为g(3+x)为偶函数,g(x)=f '(x+1),所以f '(x+4)=f '(-x+4),
对f(2+x)-f(2-x)=4x两边同时求导,得f '(2+x)+f '(2-x)=4,所以有
f '(4+x)+f '(-x)=4⇒f '(4-x)+f '(-x)=4⇒f '(4+x)+f '(x)=4⇒f '(8+x)=f '(x),所以函数f '(x)的周期为8,在f '(2+x)+f '(2-x)=4中,令x=0,得f '(2)=2,因此g(17)=f '(18)=f '(2)=2.
因为g(3+x)为偶函数,所以有g(3+x)=g(3-x)⇒g'(3+x)=-g'(3-x)⇒
g'(7)=-g'(-1) ①,
f '(8+x)=f '(x)⇒g(7+x)=g(x-1)⇒g'(7+x)=g'(x-1)⇒g'(7)=
g'(-1) ②,
由①②可得:g'(7)=0,所以g'(7)+g(17)=2,故选C.
11.[多选/2024辽宁开学考试]已知函数y=xf(x)是R上的偶函数,f(x-1)+f(x+3)=0,当x∈[-2,0]时,f(x)=2x-2-x+x,则( ACD )
A.f(x)的图象关于直线x=2对称
B.4是f(x)的一个周期
C.f(x)在(0,2]上单调递增
D.f(2 024)<f(12)<f(0.50.2)
解析 由函数y=xf(x)是R上的偶函数可知,f(x)为奇函数,则f(-x)=-f(x).
又f(x-1)+f(x+3)=0,得f(x)+f(x+4)=0,则f(x+4)=-f(x)=
f(-x),所以f(x+2)=f(2-x),则f(x)的图象关于直线x=2对称,A项正确.
由f(8+x)=-f(4+x)=f(x)可知,8是f(x)的一个周期,由f(x)=-f(x+4)可知,4不是f(x)的一个周期,B项错误.
当x∈[-2,0]时,易知f(x)=2x-2-x+x为增函数,
又f(x)为奇函数,所以f(x)在(0,2]上单调递增,C项正确;
又f(2 024)=f(8×253)=f(0),0<0.5<0.50.2,且f(x)在[-2,2]上单调递增,所以f(0)<f(12)<f(0.50.2),即f(2 024)<f(12)<f(0.50.2),D项正确.故选ACD.
12.[多选/2024江西分宜中学、临川一中等校联考]已知函数y=f(x)对任意实数x,y都满足2f(x)f(y)=f(x+y)+f(x-y),且f(1)=-1,则( AC )
A.f(x)是偶函数B.f(x)是奇函数
C.f(x)+f(1-x)=0D.∑k=12 025f(k)=1
解析 在2f(x)f(y)=f(x+y)+f(x-y)中,令x=1,y=0,可得2f(1)f(0)=2f(1),即-2f(0)=-2,解得f(0)=1≠0,故f(x)不是奇函数,B错误;令x=0可得2f(0)f(y)=f(y)+f(-y),即f(y)=f(-y),故函数f(y)是偶函数,即f(x)是偶函数,故A正确;令x=y=12,则2f2(12)=f(1)+f(0)=0,故f(12)=0,令x=12,可得2f(12)f(y)=f(12+y)+f(12-y)=0,故f(x)+f(1-x)=0,故C正确;因为f(x)是偶函数,所以f(x)=f(-x),故f(-x)+f(1-x)=0,即
f(x)+f(1+x)=0,所以f(x+1)+f(2+x)=0,所以f(x+2)=f(x),故函数
f(x)的周期为2,因为f(1)+f(0)=0,f(1)=-1,所以f(1)+f(2)=f(1)+f(0)=0,f(2 025)=f(1)=-1,所以∑k=12 025f(k)=f(1)+f(2)+…+
f(2 025)=f(2 025)=f(1)=-1,故D错误.故选AC.
13.[多选/2024南昌市模拟]f(x)是定义在R上的连续可导函数,其导函数为f'(x),下列说法中正确的是( ACD )
A.若f(x)=f(-x),则f'(x)=-f'(-x)
B.若f'(x)=f'(x+T)(T≠0),则f(x)=f(x+T)
C.若f(x)的图象关于点(a,b)中心对称,则f'(x)的图象关于直线x=a轴对称
D.若f(-1+x)+f(-1-x)=2,f'(x+2)的图象关于原点对称,则f(-1)+
f'(2)=1
解析 对于A:f(x)=f(-x)两边对x求导,得f'(x)=-f'(-x),故A正确.
对于B:f(x)=f(x+T)+C(C为常数)⇔f'(x)=f'(x+T),则C≠0时,B错误.
对于C:f(x)的图象有对称中心(a,b)⇒f(a-x)+f(a+x)=2b,两边对x求导,得-f'(a-x)+f'(a+x)=0,即f'(a-x)=f'(a+x)⇒f'(x)的图象关于直线x=a对称,C正确.
对于D: f(-1+x)+f(-1-x)=2⇒f(x)的图象有对称中心(-1,1),则
f(-1)=1.f'(x+2)的图象向右平移2个单位长度f'(x)的图象⇒f'(x)的图象有对称中心(2,0),则f'(2)=0.所以f(-1)+f'(2)=1+0=1,故D正确.故选ACD.
14. [2022全国卷乙]若f(x)=ln|a+11-x|+b是奇函数,则a= -12 ,b= ln2 .
解析 解法一 f(x)=ln|a+11-x|+b=ln|a+11-x|+ln eb=ln|(a+1)eb-aebx1-x|.
∵f(x)为奇函数,
∴f(-x)+f(x)=ln|(a+1)2e2b-a2e2bx21-x2|=0,
∴|(a+1)2e2b-a2e2bx2|=|1-x2|.
当(a+1)2e2b-a2e2bx2=1-x2时,(a+1)2e2b=1,a2e2b=1,解得a=-12,b=ln2.
当(a+1)2e2b-a2e2bx2=-1+x2时,(a+1)2e2b=-1,a2e2b=-1,无解.
综上,a=-12,b=ln 2.
解法二 易知x≠1.∵函数f(x)为奇函数,
∴由奇函数定义域关于原点对称可得x≠-1,
∴当x=-1时,|a+11-x|≤0.
又∵|a+11-x|≥0恒成立,
∴当x=-1时,|a+11-x|=0,
∴a=-12.
又由f(0)=0可得b=ln 2.
经检验符合题意,∴a=-12,b=ln 2.
15.[探索创新/2023广西联考]若定义在D上的函数f(x)满足下列条件:①∀x∈D,
f(x-2)+f(2-x)=0恒成立;②∀x1,x2∈D,当x1≠x2时,x1 f(x1)+x2 f(x2)>
x1 f(x2)+x2 f(x1)恒成立;③∀x1∈R,∃x2∈D,使得f(x2)·2x1=1成立.则称该函数为“χ函数”,下列函数可以称为“χ函数”的是( D )
A.f(x)=1-3x3x+1+3B.f(x)=2+sin x
C.f(x)=x4-x2+1D.f(x)=ln(x2+1+x)
解析 由①∀x∈D,f(x-2)+f(2-x)=0恒成立可知,y=f(x)的图象关于原点对称,“χ函数”为奇函数.
②∀x1,x2∈D,当x1≠x2时,x1 f(x1)+x2 f(x2)>x1 f(x2)+x2 f(x1)恒成立,整理可得(x1-x2)[f(x1)-f(x2)]>0,所以函数y=f(x)在D上单调递增.③∀x1∈R,∃x2∈D,使得f(x2)·2x1=1成立,整理可得f(x2)=(12)x1,因为∀x1∈R,y=(12)x1>0,所以(0,+∞)是f(x)的值域的子集.
对于选项B,C,均不满足①,对于选项A,f(x)=1-3x3x+1+3=2-(3x+1)3(3x+1)=23(3x+1)-13,在定义域内单调递减,不满足②,f(x)=ln(x2+1+x)满足①②③,故选D.课标要求
命题点
五年考情
命题分析预测
1.了解奇偶性的概念和几何意义.
2.了解周期性的概念和几何意义.
函数的奇偶性
2023新高考卷ⅠT11;2023新高考卷ⅡT4;2023全国卷乙T4;2023全国卷甲T13;2022新高考卷ⅠT12;2022全国卷乙T16;2021全国卷乙T4;2021全国卷甲T12;2021新高考卷ⅠT13;2021新高考卷ⅡT8;2021新高考卷ⅡT14;2020全国卷ⅡT9;2020新高考卷ⅠT8;2019全国卷ⅡT14;2019全国卷ⅢT11
本讲为高考命题重点,命题热点有函数奇偶性的判断,利用函数的奇偶性求解析式、求函数值、解不等式等,函数周期性的判断及应用.题型以选择题、填空题为主,函数性质综合命题时难度中等偏大.预计2025年高考命题稳定,备考时注重常规题型训练的同时,关注命题角度创新试题及抽象函数性质的灵活运用.
函数的周期性
2022新高考卷ⅠT12;2022新高考卷ⅡT8;2022全国卷乙T12
函数图象的对称性
2022全国卷乙T12
函数性质的综合应用
2022新高考卷ⅠT12;2022全国卷乙T12;2021新高考卷ⅡT8;2021全国卷甲T12;2020新高考卷ⅠT8;2019全国卷ⅢT11
奇偶性
定义
图象特征
特性
单调性
奇函数
一般地,设函数f(x)的定义域为D,如果∀x∈D,都有-x
∈D,且①f(-x)=-f(x) ,那么函数f(x)就叫做奇函数.
关于②原点对称.
(1)如果定义域中包含0,那么 f(0)=③ 0 .
(2)若函数在关于原点对称的区间上有最值,则f(x)max+
f(x)min=④ 0 .
在关于原点对称的区间上单调性⑤ 相同 .
偶函数
一般地,设函数f(x)的定义域为D,如果∀x∈D,都有-x
∈D,且⑥ f(-x)=f(x) ,那么函数f(x)就叫做偶函数.
关于⑦ y轴 对称.
f(x)=f(|x|).
在关于原点对称的区间上单调性⑧ 相反 .
抽象函数性质
基本函数模型
f(x±y)=f(x)±f(y)∓b
一次函数f(x)=kx+b(k≠0)
f(x+y)=f(x)+f(y)+2xy
二次函数f(x)=x2+bx
f(xy)=f(x)f(y)或f(xy)=f(x)f(y)
幂函数f(x)=xα
f(x+y)=f(x)f(y)或f(x-y)=f(x)f(y)
指数函数f(x)=ax(a>0,且a≠1)
f(xy)=f(x)+f(y)或f(xy)=f(x)-f(y)
对数函数f(x)=lgax(a>0,且a≠1)
f(x+y)+f(x-y)=2f(x)f(y)
余弦函数f(x)=cs ωx(ω一般取满足要求的最小正数)
2025年高考数学精品教案第二章 函数 第1讲 函数的概念及其表示: 这是一份2025年高考数学精品教案第二章 函数 第1讲 函数的概念及其表示,共12页。
2025年高考数学精品教案第二章 函数 第2讲 函数的单调性与最值: 这是一份2025年高考数学精品教案第二章 函数 第2讲 函数的单调性与最值,共17页。
高考数学一轮复习教案 第2章_第3节_函数的奇偶性与周期性(含答案解析): 这是一份高考数学一轮复习教案 第2章_第3节_函数的奇偶性与周期性(含答案解析),共14页。












